刷四百道题总结的24种常用的刷题思路
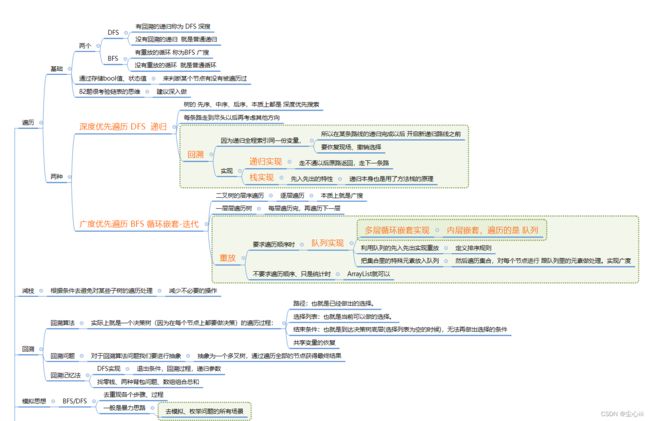
1、树的两种遍历
DFS 有回溯的递归称为 DFS 深搜
没有回溯的递归 就是普通递归
BFS 有重放的循环 称为BFS 广搜
没有重放的循环 就是普通循环
深度优先遍历 DFS
树的 先序、中序、后序,本质上都是 深度优先搜索
每条路走到尽头以后再考虑其他方向
回溯思想,因为递归全程索引同一份变量,所以在某条路线的递归完成以后 开启新递归路线之前,要恢复现场、撤销选择
实现方式
递归实现,走不通以后原路返回,走下一条路
栈实现,先入先出的特性,递归本身也是用了方法栈的原理
广度优先遍历 BFS 循环嵌套-迭代
二叉树的层序遍历,逐层遍历,本质上就是广搜
一层层遍历树,每层遍历完,再遍历下一层
重放思想,要求遍历顺序时
队列实现,多层循环嵌套实现,内层嵌套,遍历的是 队列
利用队列的先入先出实现重放,定义排序规则
把集合里的特殊元素放入队列,然后遍历集合,对每个节点进行 跟队列里的元素做处理。实现广度,不要求遍历顺序、只是统计时
ArrayList、优先队列、数组、栈等看具体场景
2、减枝
根据条件去避免对某些子树的遍历处理,减少不必要的操作
3、回溯
回溯算法,实际上就是一个决策树(因为在每个节点上都要做决策)的遍历过程:
1路径:也就是已经做出的选择。
2选择列表:也就是当前可以做的选择。
3结束条件:也就是到达决策树底层(选择列表为空的时候),无法再做出选择的条件
4共享变量的恢复
回溯问题
对于回溯算法问题我们要进行抽象,抽象为一个多叉树,通过遍历全部的节点获得最终结果
回溯记忆法,DFS实现,退出条件,回溯过程,递归参数
如 :找零钱、两种背包问题、数组组合总和
4、模拟思想
BFS/DFS去重现各个步骤、过程,
一般是暴力思路,去模拟、枚举问题的所有场景
5、动态规划 DP思想
分析三步走
1找到 重叠子问题
穷举所有场景
画出树/表格 分析出重叠的子问题
然后决定遍历时怎么处理
分析 最优子结构
分解问题
然后求出每部分的最优解
如 学生想考第一名
需要每科都考第一
2初始状态定义
3列出 状态转移方程
例子
兔子,重叠子问题,每个子问题都需要重复计算多次
DP数组,重叠子问题
备忘录,重叠子问题
凑零钱,最值问题
青蛙跳台阶,最值问题
最长递增子序列
背包问题,完全背包,0-1背包问题
6、滚动数组
对DP数组进行空间压缩 二维变一维,一维变常量级
即:即只记录、维护几个相关的dp值
7、贪心思想
问题分解成多个子问题,子场景
然后求出每个场景下的最优解,然后比较出最优解里的最值
dp 贪心是最难的,看运气
8、优先级队列
大顶堆 小顶堆:应用场景:去求top k,堆排序、中位数
新增,上滤 上浮
新元素增到堆尾,然后比较它跟父节点的关系
然后交换它跟父节点的位置
直到满足关系为止,或者是到根节点为止
删除,下滤 下沉
从被删除的位置开始下滤,取出被删除节点的最小/大的子节点
然后比较此子和它的子的子的大小,然后交互子 与子子的位置
直到满足关系为止,或者是到叶子结点为止
9、双指针
双指针去遍历 链表数组
控制指针移动机制,减少遍历循环次数
因为快慢指针同时走 所以需额外判断 fast.next 可能走过头
如:while(fast!=null && fast.next!=null){
双层循环嵌套时,i j 作为双指针
快慢指针策略
快指针每次走3步,慢指针每次走1步
快指针每次走2步,慢指针每次走1步
快指针每次走4步,慢指针每次走3步
策略不同 效果有显著差异
10、滑动窗口
赊账、还账的概念
赊账时 right++,提前消费
还账时left++,补充窗口
两种实现
队列容器实现
集合、队列存储窗口数据
双指针去控制窗口大小
左右指针在原容器的基础上维持一个虚拟窗口,维护 额外变量,记录窗口属性
11、二分思想
二分的本质是「二段性」而非「单调性」
一定满足/不一定满足某个条件时 也可以二分
12、位图思想
ASCLL码+位图 去记录字符/数字的偏移量。解决字符串的问题
纯字母的话 26个就够了。只需记录偏移量
int[26],char[c - 'a']
char[c - '1'],记录数字时
13、数组思想
大多数的哈希表计数问题,都能转换为使用数组解决
1、传播问题
通过偏移去计算某节点 周围的四个点的坐标,然后遍历四个节点,去递归处理
int[] dj=new int[]{0,0,1,-1}
int[] di=new int[]{1,-1,0,0}
2、起点,没必要局限于左上角
当矩阵是有序/有规律时,如:240 搜索二维矩阵2,从右上角,左下角去遍历 可能更合适
3、邻接表数组,用数组存储单链表,如:二叉树中所有距离为k的节点
4、长度为n的数组,每个元素都在范围 [1, n]内,肯定是要考 hash表
修改当前元素值,把原数组作为hash表,如:lc的 442题
5、栈/队列里存 数组下标 而非数组值
因为由数组下标取值很方便,而由值取数组下标不是很方便!!!!!
14、分治思想
二分法、归并排序就是分治思想
如:累加求最值,零食方法数,归并排序
15、位运算,最喜欢也最讨厌的解题思路
(n >>1)要加括号, 优先级低于+
1 与或非
|是按位 或,两个位都是0时,结果是0,否则为1
^是按位 异或,两个位相同为0,不同为1
一个数和 0 做 ^ 运算等于本身
一个数和其本身做 ^ 运算等于 0
&是按位 与,两个位都是1时,结果是1,否则为0
判断奇偶,一个数 & 1的结果就是取二进制的最末位
最末位为1表示该数为奇数。
若n是2的幂,则:n > 0,(n & (n - 1)) = 0
~ 是按位取反
2位运算
<<,位左移 乘以,3 <<2 = 12,相当于 3 *2*2 =12
>>,位右移 除以
>>>,无符号位右移,无论值的正负,都在高位补0.
16、JDK内置的方法实现
直接调用内置方法实现
例如
1 TreeSet
基于二分法实现,自己不想写二分法时,就可以使用它
floor(E e)
返回小于或等于e的最大元素,如果没有这样的元素,则返回null。
ceiling(E e)
返回大于或等于e的最大元素,如果没有这样的元素,则返回null。
2 Character
Character.toLowerCase(str)
字符串里的大写转化成小写字母
Character.isLetterOrDigit(s)
判断字符是否属于字母或十进制数字类别,若是 则true
Character.isDigit
判断字符是否是 数字类型的字符串,若是 则true
3 map.computeIfAbsent(key,value)
如果map里不存在这个key,则添加它 put(key,value)
map.compute方法
compute 给出一个key值和一个函数,然后这个函数根据key对应的键值对[key,value]计算出一个新的value,就叫newValue吧
4 String
deleteCharA t删除指定位置的元素,模拟出栈
String.join
例子:String.join("-",“a”,“b”,“c”,“d”);结果a-b-c-d
5、Math
Math.ceil
向上取整 4.1 ->5
Math.sqrt()
函数返回一个数的平方根
Math.pow(底数x,指数y)
Math.pow(2, 3) 计算2的三次方
其他过多不一一列举
17、Stream流思想
18、快速幂
扩大底数减少指数,矩阵快速幂
20、有限状态自动机
把数组转化成几种状态去表示
21、Floyd算法
处理多源最短路径适合用Floyd算法
22、KMP算法,
如果已经匹配的字符串包含相同的前缀和后缀,遇到下一个不匹配的位置时,
指向needle的指针跳转到前缀的后一个位置,还是不匹配的话,
再往前跳转后继续比较;先构造一个next数组来记录needle指针跳转的位置
KMP算法是一种改进的字符串匹配算法
23、数学规律法
多找几个样例、列举各个步骤、分析规律。找到规律,然后实现规律。
24、打表
把所有结果放入集合里,可以手动写,也可以代码生成
然后遍历集合去查询