FPGA_状态机工作原理

状态机工作原理

状态机全称是有限状态机（Finite State Machine、FSM），是表示有限个状态以及在这些状态之间的转移和动作等行为的数学模型。

状态机分为摩尔（Moore）型有限状态机与米利（Mealy）型有限状态机。摩尔状态机输出是只由输入确定的有限状态机（不直接依赖于当前状态）。米利有限状态机的输出不止与其输入有关还于它的当前状态相关，这也是与摩尔有限状态机的不同之处。

➢ Mealy 状态机：组合逻辑的输出不仅取决于当前状态，还取决于输入状态。
➢ Moore 状态机：组合逻辑的输出只取决于当前状态。

Mealy 状态机模型

Moore 状态机模型

状态机描述方式

可分为一段式、两段式以及三段式。
一段式，整个状态机写到一个 always 模块里面。在该模块中既描述状态转移，又描述状态的输入和输出。

两段式，用两个 always 模块来描述状态机。其中一个 always 模块采用同步时序描述状态转移，另一个模块采用组合逻辑判断状态转移条件，描述状态转移规律及其输出。

三段式，在两个 always 模块描述方法基础上，使用三个 always 模块，一个 always 模块采用同步时序描述状态转移，一个 always 采用组合逻辑判断状态转移条件，描述状态转移规律，另一个 always 模块描述状态输出(可以用组合电路输出，也可以时序电路输出)。实际应用中三段式状态机使用最多，因为三段式状态机将组合逻辑和时序分开，有利于综合器分析优化以及程序的维护；并且三段式状态机将状态转移与状态输出分开，使代码看上去更加清晰易懂，提高了代码的可读性，推荐大家使用三段式状态机，本文也着重讲解三段式。

三段式状态机的基本格式是：
第一个 always 语句实现同步状态跳转；
第二个 always 语句采用组合逻辑判断状态转移条件；
第三个 always 语句描述状态输出(可以用组合电路输出，也可以时序电路输出)。在开始编写状态机代码之前，一般先画出状态跳转图，这样在编写代码时思路会比较清晰，下面以一个 7 分频为例（对于分频等较简单的功能，可以不使用状态机，这里只是演示状态机编写的方法），状态跳转图如下图所示：

代码格式

状态跳转图画完之后，接下来通过 parameter 来定义各个不同状态的参数，如下

parameter S0 = 7'b0000001; //独热码定义方式
parameter S1 = 7'b0000010;
parameter S2 = 7'b0000100;
parameter S3 = 7'b0001000;
parameter S4 = 7'b0010000;
parameter S5 = 7'b0100000;
parameter S6 = 7'b1000000;

这里是使用独热码的方式来定义状态机

接下来还需要定义两个 7 位的寄存器，一个用来表示当前状态，另一个用来表示下一个状态，如下所示：

reg [6:0] curr_st ; //当前状态
reg [6:0] next_st ; //下一个状态

接下来就可以使用三个 always 语句来开始编写状态机的代码，第一个 always 采用同步时序描述状态
转移，第二个 always 采用组合逻辑判断状态转移条件，第三个 always 是描述状态输出，一个完整的三段
式状态机的例子如下代码所示：

module divider7_fsm (
//系统时钟与复位
input sys_clk ,
input sys_rst_n ,

//输出时钟
output reg clk_divide_7 
);

 //parameter define 
 parameter S0 = 7'b0000001; //独热码定义方式
 parameter S1 = 7'b0000010;
 parameter S2 = 7'b0000100;
 parameter S3 = 7'b0001000;
 parameter S4 = 7'b0010000;
 parameter S5 = 7'b0100000;
 parameter S6 = 7'b1000000; 
 
 //reg define 
 reg [6:0] curr_st ; //当前状态
 reg [6:0] next_st ; //下一个状态

 //*****************************************************
 //** main code
 //***************************************************** 

 //状态机的第一段采用同步时序描述状态转移
 always @(posedge sys_clk or negedge sys_rst_n) begin
	 if (!sys_rst_n)
		curr_st <= S0;
	 else
		curr_st <= next_st;
 end

 //状态机的第二段采用组合逻辑判断状态转移条件
 always @(*) begin
		 case (curr_st)
		 S0: next_st = S1;
		 S1: next_st = S2;
		 S2: next_st = S3;
		 S3: next_st = S4;
		 S4: next_st = S5;
		 S5: next_st = S6;
		 S6: next_st = S0;
		 default: next_st = S0;
	 endcase
 end

 //状态机的第三段描述状态输出（这里采用时序电路输出）
 always @(posedge sys_clk or negedge sys_rst_n) begin
	if (!sys_rst_n)
		clk_divide_7 <= 1'b0;
	 else if ((curr_st == S0) | (curr_st == S1) | (curr_st == S2) | (curr_st == S3))
		clk_divide_7 <= 1'b0;
	 else if ((curr_st == S4) | (curr_st == S5) | (curr_st == S6))
		clk_divide_7 <= 1'b1; 
	 else
	 ;
 end

 endmodule

总结

从代码中可以看出，输出的分频时钟 clk_divide_7 只与当前状态（curr_st）有关，而与输入状态无关，所以属于摩尔型状态机。状态机的第一段对应摩尔状态机模型的状态寄存器，用来记忆状态机当前所处的状态；状态机的第二段对应摩尔状态机模型产生下一状态的组合逻辑 F；状态机的第三段对应摩尔状态机产生输出的组合逻辑 G，因为采用时序电路输出有很大的优势，所以这里第三段状态机是由时序电路
输出的。

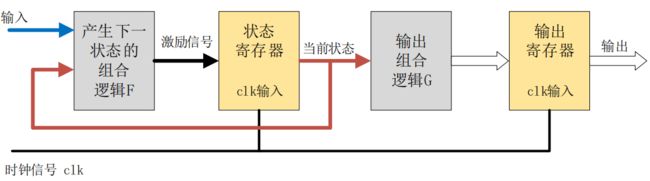
状态机时序电路输出模型

采用这种描述方法虽然代码结构复杂了一些，但是这样做的好处是可以有效地滤去组合逻辑输出的毛刺，同时也可以更好的进行时序计算与约束，另外对于总线形式的输出信号来说，容易使总线数据对齐，减小总线数据间的偏移，从而降低接收端数据采样出错的频率。