<排序算法二>层层深入,从堆开始理解“堆排序”
1.导入:堆是啥
提到堆,我们首先想到的它是一个形容词,诸如“堆叠”,“一堆杂物”等。同时它也可以指某个事物,如“三星堆”、“罗汉堆”、“沙堆”等。
我们这里说的堆是指是数据结构中的堆,如果说石堆是用石头堆砌的,叠罗汉是由人搭成的话,那堆就是一个数据堆成的,类似于塔形的结构,它有如下定义:
堆是具有下列性质的完全二叉树:每个节点的值都大于或等于其左右孩子节点的值,称之为大根堆;或者每个节点的值都小于或等于其左右孩子节点的值,称之为小根堆。(注:对二叉树不了解的同学建议先了解一下二叉树)
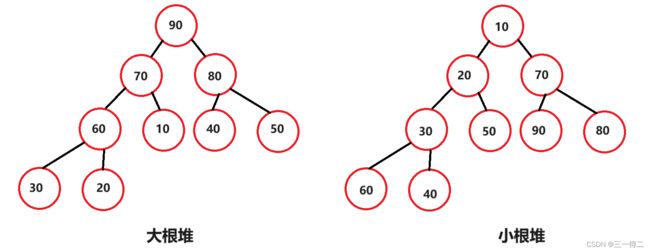
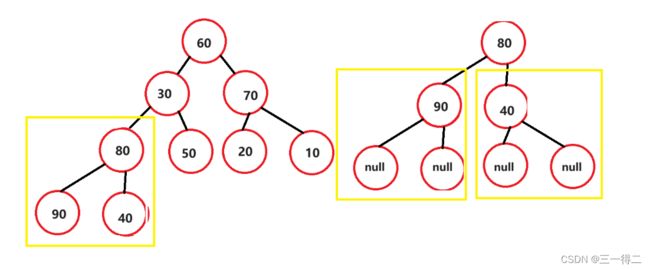
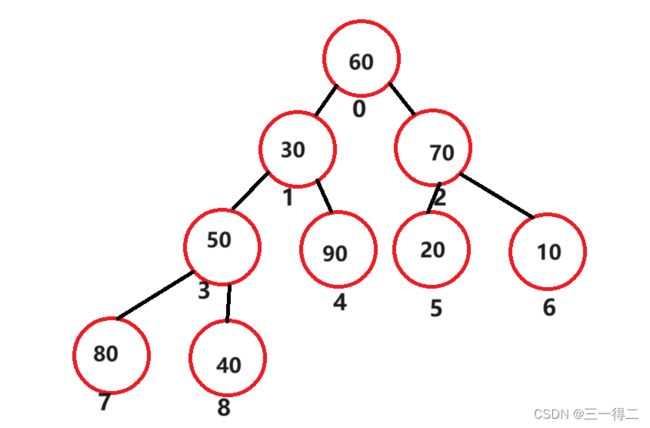
文字的描述并不直观,通过图片来看更加容易理解,如以一组数据{90,70,80,60,10,40,50,30,20}为例,其堆结构表现可以如图。
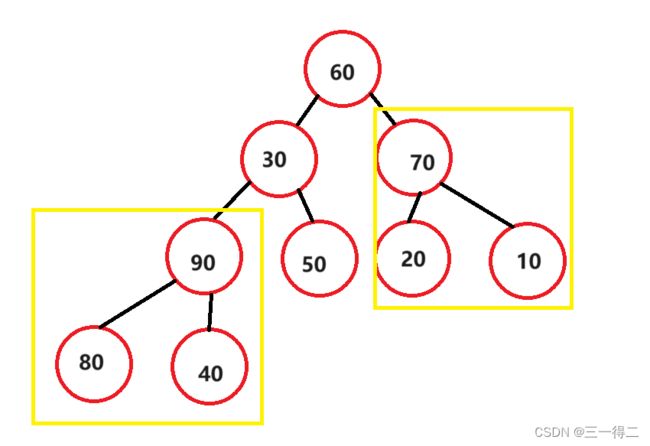
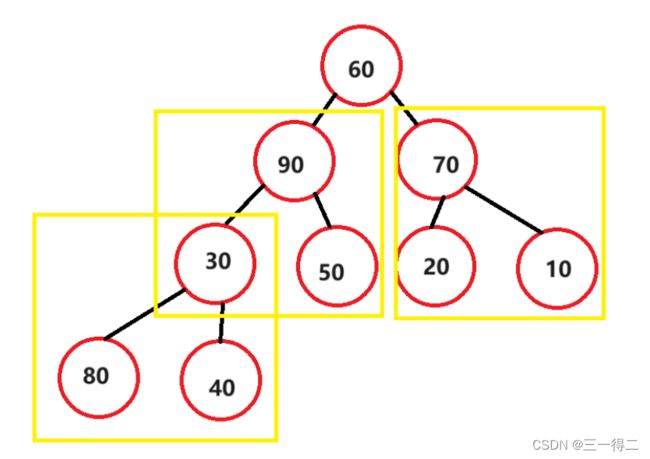
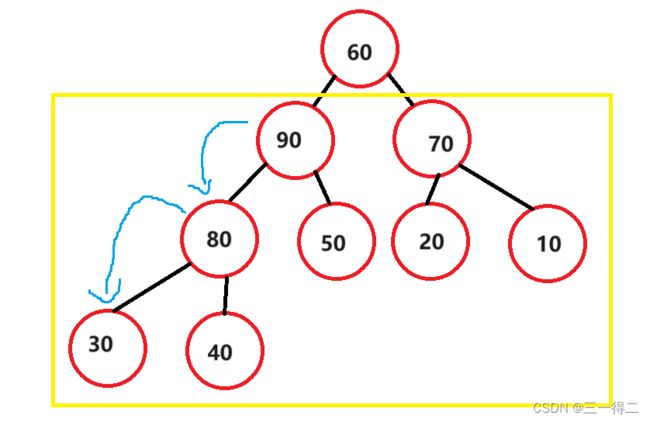
从图中我们可以观察到,左右图都是完全二叉树,只不过其排序方式并不同,左图遵循每个节点的值都比他的左右孩子的值要大,而右图每个节点的值都小于或等于其左右孩子节点的值。
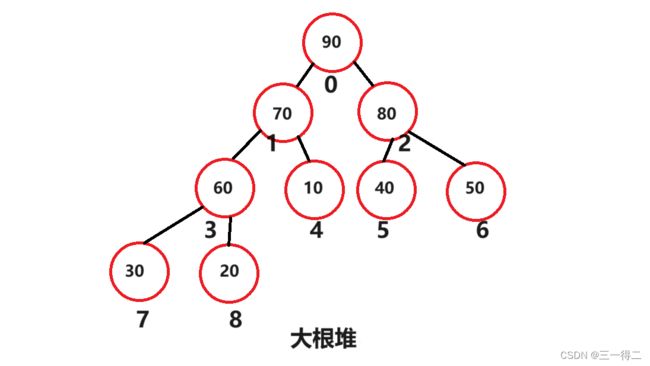
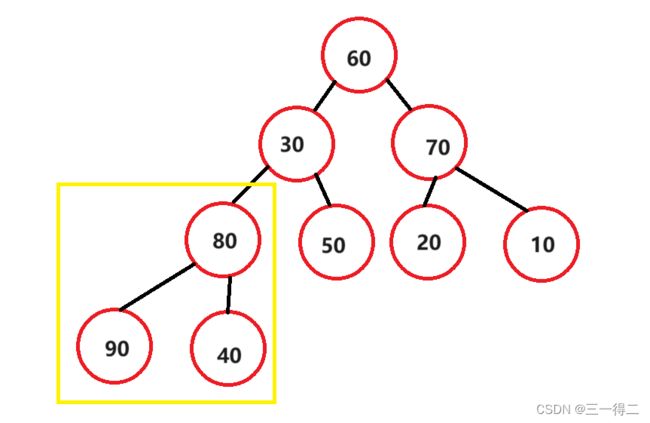
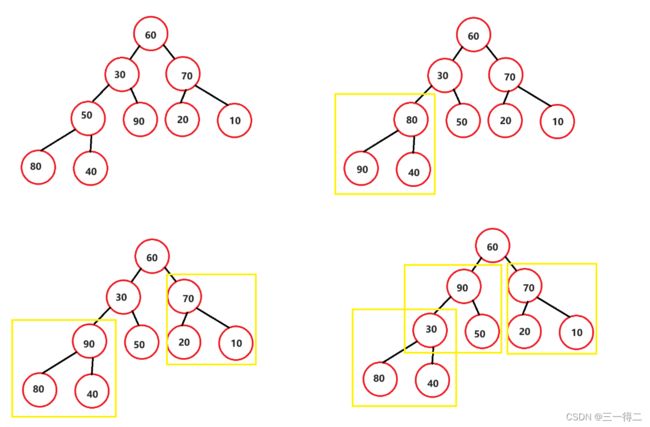
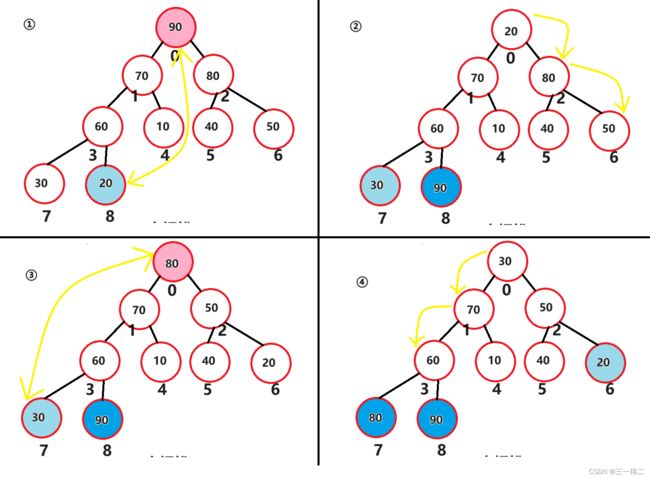
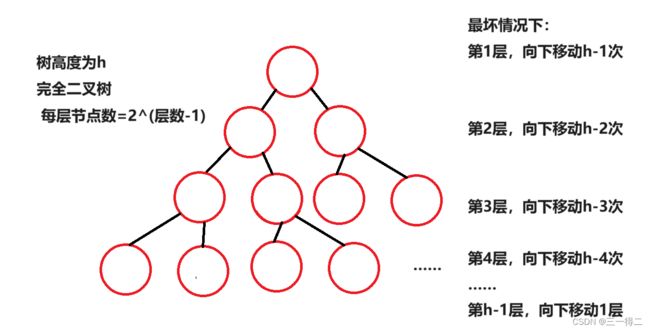
但这并不能说其是有序的,也不能说明a>b或a 好了,对堆有了初步的了解后,我们进入下一步,找到堆可以用来排序的特性。 如果想要对堆进行排序,能够精准的找到每个节点是非常有必要的,对堆按照层序遍历循序进行编号后,就得到如下图: 设堆的节点总数为n,节点90为 当满足 最后我们将编号后的堆按编号存入数组。 好了,我们现在已经可以通过堆根与左右树的关系将数组和堆建立联系,可以轻松找到数组成员在堆中对应的左右树根节点,如array[3]对应左根array[7]及右根array[8],array[1]对应左根array[3]及右根array[4],接下来进入正题,堆排序。 堆中节点向下调整是堆排序的关键,也是建堆的关键,因此必须导一下子,毕竟是从零到一吗~ 问题1:向下调整,调整什么? 答:向下调整该节点,使该节点的位置满足堆“每个节点的值都大于或等于其左右孩子节点的值”,同时不破坏堆的有序结构。 问题2:怎么调整? 先从小树着手,有二叉树如上图,若对节点80进行向下调整该怎么调?很简单,对其左右孩子节点进行判断,找出节点值最大的一个,用最大的节点来和节点80比,若80节点没有最大的孩子节点大,那么就和这个大孩子节点互换。 示例中90>40,90>80,因此80节点和90节点互换,此树局部满足堆的要求。 再调整一个小树,对70所在节点进行向下调整,20>10,70>20,节点70所在子树满足堆要求。 接着,向下调整30节点所在深度为3的子树,因为90节点所在子树已经满足条件,我们只要在保证其仍满足条件的情况下让30节点及其左右孩子部分满足条件就行了。 进行同样的判断交换操作,90>50,90>30,90节点和30节点互换,如下。 调整后我们如愿使该部分满足了条件,但通过观察发现,30节点的向下调整破坏了被换位置所在子树的结构,使其不再满足成堆的条件,不过没关系,我们在调整后再次进行向下调整不就行了。 原理剖析:下移的原因是小于大孩子节点的值(90),而大孩子节点原先必定满足节点的值大于或等于其左右孩子节点的值这一成堆条件,因此即便对下移后的节点再次向下调整,接替节点的值也必定小于大孩子节点的值 此时,我们得到了一个除了根节点之外其余部分全部满足成堆条件的完全二叉树,接下来对根节点,不断进行向下调整,就得到了一个大根堆。 最终结论:对一个除根节点外所有子树均满足成堆条件的完全二叉树而言,对其根节点不断进行向下调整,当无法进行向下调整时将得到一个堆。 大视角验证:对深度为4的完全二叉树如上图,其除根节点外所有子树均满足成堆条件,完成根节点向下调整后成功得到堆。 小视角验证:对于只有三个节点的子树,我们可以认为其左右孩子节点是左右孩子均为空节点的子树;孩子节点唯一具有值,默认为最大值,认为其满足成堆条件,即叶子节点同样认为该部分满足成堆条件。由此推得三节点子树是“ 除根节点外所有子树均满足成堆条件的完全二叉树 ”,对其根节点向下调整后得到三节点堆。 向下调整代码实现: 首先需要一组数据,array = {60,30,70,50,90,20,10,80,40} 根据“2导入:堆与数组”得到的结论模拟构建一个完全二叉树 由“3导入:建堆”得到的结论可知,如果能使一个完全二叉树除根外都满足成堆条件,则只要对其根节点进行向下调整便能得到堆 问题:如何使一个完全二叉树除根外都满足成堆条件 答:从最后一个有子节点的子树开始对其根节点进行向下调整,即按照编号从 原理剖析:从小树调整至大树,首先是深度为2的子树,接着是深度为3的子树,接着是深度为4的子树……在这一过程中,调整较大树之前所有较小树(一定包括较大树的子树)都被调整过,所以每次调整都能使较大树成堆,直至调整完整个完全二叉树有孩子的根节点。 无序数组转大根堆代码实现: 堆排序(Heep Sort)就是利用堆(假设利用大根堆)进行排序的方法。他它的基本思想是,将待排序的序列构造成一个大根堆。此时,整个序列的最大值就是树的根节点。将它移走(其实就是将其与堆数组的末尾元素交换,那么末尾元素就变成了最大值),然后将剩余的n-1个序列重新构造成一个堆,这样就会再次在堆顶(根节点)得到n个元素中的次级最大值。如此反复执行,便能得到一个有序序列了。 需要注意的是排升序要建大堆,排降序建小堆。 图中深蓝色节点为填入最大值的部分,浅蓝色节点为下一次和最大值交换的节点,粉色节点为序列中预交换的最值节点,黄线为交换路径。 图解,图①是一个大根堆,根节点是最大值,将其与末尾节点8进行互换,得到如图②,末尾节点-1变为7;图②中对节点0进行向下调整,分别和节点2和节点6互换,的到如图③,完全二叉树恢复为序列0~7的大根堆;图③中序列0~7的大根堆将根节点0值(序列最大值)和末尾节点7交换,得到如图④,末尾节点-1变为6;图④中根节点向下调整,分别于节点1和节点3互换(深蓝色节点不在序列内),将完全二叉树恢复为序列0~6的大根堆……后续以此类推,请自行脑补(博主手要废了)。 相信同学你已经有些明白堆排序的基本思想了,下面分阶段实现代码: 第一部分,实现向下调整,思想参考“3前置:堆与向下调整”: 第二部分,实现将无序数组转换为大根堆数组,思想参考“4前置:建堆”: 第三部分,实现首尾交换,按序列对根节点向下调整,思想参考“5.堆排序算法”介绍和图解部分: 全部代码,可以调试运行一下: 堆排序的运行时间主要消耗在初始创建堆和在恢复堆的反复筛选上。 在构建堆的过程中,需要我们从h-1层的那个非终端节点开始遍历,在最坏情况下向下调整节点需要将其移动到最后一层h层,且堆为满二叉树,如下图: 那么对于要建高度为h的堆,最坏情况下要移动SUM次 错位相减法: 2SUM-SUM≈2∧(h-1) N=2∧h - 1 得:SUM=log(N) 移动次数即为构建堆的最终时间复杂度,O(log(n)) 在正式排序时,第i次取堆顶记录重建堆需要用O(logi)的时间(完全二叉树的某个结点到根结点的距离为[logzi]+1),并且需要取n-1次堆顶记录,因此,重建堆的时间复杂度为O(nlogn)。 所以总体来说,堆排序的时间复杂度为 O(nlogn)。 总结: 空间复杂度低,它只有一个用来交换的暂存单元 由于初始构建堆所需的比较次数较多,因此,它并不适合待排序序列个数较少的情况。 由于记录的比较与交换是跳跃式进行,因此堆排序也是一种不稳定的排序方法。 感谢观看,如果本篇文章对您有帮助的话,不妨为博主留下一个赞鼓励一下吧,谢谢啦~ 2.导入:堆与数组
![]() ,70为
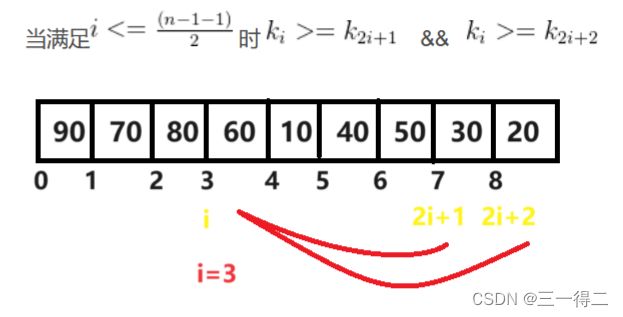
,70为![]() ……根据完全二叉树的性质,结点的左树根节点编号为自身节点编号*2+1,而堆共有n个节点,第n个节点是堆得最后一个节点,其父节点是最后一个有孩子子节点的节点,由此可得:
……根据完全二叉树的性质,结点的左树根节点编号为自身节点编号*2+1,而堆共有n个节点,第n个节点是堆得最后一个节点,其父节点是最后一个有孩子子节点的节点,由此可得:![]() 时
时 ![]() &&
&& ![]()
3.前置:堆与节点向下调整
public void swap(int[] array, int s, int k) {
int cur = array[s];
array[s] = array[k];
array[k] = cur;
}
public void heapAdjust(int[] array, int index) {
//array目标数组
//index须向下调整节点位置
//chile保存被调整节点孩子节点的下标,初始值为左孩子下标
int chile = (index*2)+1;
//不能越界
while(chile < array.length) {
//左孩子节点值<右孩子节点值,则使chile保存右孩子节点下标
if(chile+1 < array.length && array[chile] < array[chile+1]) {
chile = chile + 1;
}
//当被调整节点大于左右孩子中的最大值,那么此时无需调整直接退出程序即可
if(array[chile] < array[index]) {
break;
}
//此时被调整节点小于左右孩子中的最大值,使两者互换
swap(array, index, chile);
//更新被调整节点的位置
index = chile;
//更新被调整节点孩子节点的下标
chile = (index*2)+1;
}
}4.前置:建堆
![]() ~ 0分别进行向下调整即可(2导入:堆与数组中得到的结论,最后一个有孩子节点的子树根节点编号为
~ 0分别进行向下调整即可(2导入:堆与数组中得到的结论,最后一个有孩子节点的子树根节点编号为![]() )
) public void toHeapArray(int[] array) {
//找到倒数第一个子树的根节点下标lastIndex;
int lastIndex = (array.length-1-1)/2;
//从倒数第一个子树的根节点遍历至完全二叉树根节点,即array[0]
for(int i = lastIndex; i >= 0; i--) {
//对遍历到的根节点完成向下调整
heapAdjust(array, i, array.length);
}
}5.堆排序算法
public void swap(int[] array, int s, int k) {
int cur = array[s];
array[s] = array[k];
array[k] = cur;
}
public void heapAdjust(int[] heapArray, int index, int lastIndex) {
//heapArray大根堆数组
//index被调整节点位置,初始值为0
//lastIndex末尾节点后一位,确定序列尾
//chile保存被调整节点孩子节点的下标,初始值为左孩子下标
int chile = (index*2)+1;
//lastIndex<=heapArray.length
//末尾节点不在调整序列内
while(chile public void toHeapArray(int[] array) {
//找到倒数第一个子树的根节点下标lastIndex;
int lastIndex = (array.length-1-1)/2;
//从倒数第一个子树的根节点遍历至完全二叉树根节点,即array[0]
for(int i = lastIndex; i >= 0; i--) {
//对遍历到的根节点完成向下调整
heapAdjust(array, i, array.length);
}
} public void heapSort(int[] array) {
//将无序数组转化为大根堆数组
toHeapArray(array);
//从最后一个节点开始进行首尾交换,当i=0时末尾为自身无需交换
for(int i = array.length-1; i > 0; i--) {
//交换大根堆首尾
swap(array, 0, i);
//恢复序列[0, i)区间为大根堆,交换首尾后array[i+1]为末尾节点
heapAdjust(array, 0, i);
}
} public void swap(int[] array, int s, int k) {
int cur = array[s];
array[s] = array[k];
array[k] = cur;
}
public void heapAdjust(int[] heapArray, int index, int lastIndex) {
//heapArray大根堆数组
//index被调整节点位置,初始值为0
//lastIndex末尾节点后一位,确定序列尾
//chile保存被调整节点孩子节点的下标,初始值为左孩子下标
int chile = (index*2)+1;
//lastIndex<=heapArray.length
//末尾节点不在调整序列内
while(chile < lastIndex) {
//左孩子节点值<右孩子节点值,则使chile保存右孩子节点下标
if(chile+1 < lastIndex && heapArray[chile] < heapArray[chile+1]) {
chile = chile + 1;
}
//当被调整节点大于左右孩子中的最大值,那么此时无需调整直接退出程序即可
if(heapArray[chile] < heapArray[index]) {
break;
}
//此时被调整节点小于左右孩子中的最大值,使两者互换
swap(heapArray, index, chile);
//更新被调整接的位置
index = chile;
//更新被调整节点孩子节点的下标
chile = (index*2)+1;
}
}
public void toHeapArray(int[] array) {
//找到倒数第一个子树的根节点下标lastIndex;
int lastIndex = (array.length-1-1)/2;
//从倒数第一个子树的根节点遍历至完全二叉树根节点,即array[0]
for(int i = lastIndex; i >= 0; i--) {
//对遍历到的根节点完成向下调整
heapAdjust(array, i, array.length);
}
}
public void heapSort(int[] array) {
//将无序数组转化为大根堆数组
toHeapArray(array);
//从最后一个节点开始进行首尾交换,当i=0时末尾为自身无需交换
for(int i = array.length-1; i > 0; i--) {
//交换大根堆首尾
swap(array, 0, i);
//恢复序列[0, i)区间为大根堆,交换首尾后array[i+1]为末尾节点
heapAdjust(array, 0, i);
}
}6.堆排序算法复杂度分析
![]() 各行移动之和
各行移动之和![]()
![]()
![]()