动态规划问题
动态规划
- 1. 不相交的线
- 2. 不同的子序列
- 3. 通配符匹配
- 4. 交错字符串
1. 不相交的线
1.题目链接:不相交的线
2.问题描述:
在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。
现在,可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线,这些直线需要同时满足满足:
nums1[i] == nums2[j],且绘制的直线不与任何其他连线(非水平线)相交。
请注意,连线即使在端点也不能相交:每个数字只能属于一条连线。
以这种方法绘制线条,并返回可以绘制的最大连线数。
示例1:
输入:nums1 = [1,4,2], nums2 = [1,2,4]
输出:2
解释:可以画出两条不交叉的线,如下图所示。
但无法画出第三条不相交的直线,因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到
nums2[1]=2 的直线相交。
示例 2:
输入:nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]
输出:3
示例 3:
输入:nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1]
输出:2
提示:
1 <= nums1.length, nums2.length <= 500
1 <= nums1[i], nums2[j] <= 2000
3.问题分析:要求nums1[i] == nums2[j],且绘制的直线不与任何其他连线(非水平线)相交,我们将这些相同的数据取出来,可以看到它们刚好是两个数组中的最长公共子序列,所以这道题就是让求两个数组的最长公共子序列。假设从nums1[i]的首尾开始,然后遍历nums2[j],如果有数据相同,那么就能确定有公共子序列;然后就有两种思路,第一种,如果碰到相同的i,j都进行++操作,然后继续遍历,这种遍历出来的具有局限性,当nums1是nums2的子序列时,遍历才正确,遍历中间某一步有一个不同的话,就会出错;所以应该将nums1中的数据每一个都与nums2数组进行遍历,具体遍历如下。
- 状态表示:dp[i][j] 表⽰: nums1的 [0, i] 区间以及nums2的 [0, j] 区间内的所有的⼦序列中,最⻓公共⼦序列的⻓度。
- 状态转移方程:1.如果nums1[i] = nums2[j],那么最⻓公共⼦序列就在nums1的 [0, i - 1] 以及nums2的[0, j - 1]区间上找到⼀个最⻓的,然后再加上nums1[i] 即可。因此
dp[i][j] = dp[i - 1][j - 1] + 1。 2.如果nums1[i] != nums2[j],那么最长公共子序列可以在nums1中的(0,i - 1)和nums2中的(0,j)或者在nums1中的(0,i )和nums2中的(0,j - 1)中寻找最大值,因此dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])。 - 初始化:dp表全初始化为0即可。
- 填表顺序:要求i,j位置的dp,先要求i-1或j-1的dp,所以从上往下填写每⼀⾏,每⼀⾏从左往右。
- 返回值:根据状态表⽰得:返回 dp[m][n] 。
4.代码如下:
class Solution
{
public:
int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2)
{
int m = nums1.size(), n = nums2.size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
for (int i = 1; i <= m; ++i)
{
for (int j = 1; j <= n; ++j)
{
if (nums1[i - 1] == nums2[j - 1])
dp[i][j] = dp[i - 1][j - 1] + 1;
else
dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);
}
}
return dp[m][n];
}
};
2. 不同的子序列
1.题目链接:不同的子序列
2.题目描述:
给你两个字符串 s 和 t ,统计并返回在 s 的 子序列 中 t 出现的个数,结果需要对 109 + 7 取模。
示例 1:
输入:s = “rabbbit”, t = “rabbit”
输出:3
解释: 如下所示, 有 3 种可以从 s 中得到 "rabbit"的方案。 rabbbit rabbbit rabbbit
示例 2:
输入:s = “babgbag”, t = “bag”
输出:5
解释: 如下所示, 有 5 种可以从 s 中得到 “bag” 的方案。
babgbag babgbag babgbag babgbag babgbag
提示:
1 <= s.length, t.length <= 1000
s 和 t 由英文字母组成
3.题目分析:两个字符串s和t,其中将t看作短串,将s看作长串,从s中寻找组成t的字符串,计算组成t字符串的次数。对于两个字符串来说可以选取s中的(0, i)区间和t中的(0,j)区间当做研究对象,所以可以定义状态表示:dp[i][j] 表示在字符串s的 [0, i] 区间内的所有⼦序列中,有多少个 t 字符串 [0,j] 区间内的⼦串。然后对符合的条件进行分析,如1.当s[i] = t[j]时,此时有两种情况,一是选择s[i]做结尾,s[i] = t[j],这两个位置可以和前面的字符相结合,结合后的个数和结合前的个数是相等的,因此dp[i][j] = dp[i - 1][j - 1],二是不选s[i]做结尾,那么就在s中的(0, i - 1)区间与t中的(0, j)区间中找有多少个t的子串,此时dp[i][j] = dp[i - 1][j],所以dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];2.当**s[i] != t[j]**时,那么就只能在s中的(0, i - 1)区间与t中的(0, j)区间中找有多少个t的子串,因此dp[i][j] = dp[i - 1][j]。最后就剩下一些细节需要处理。
- 状态表示:dp[i][j] 表示在字符串s的 [0, i] 区间内的所有⼦序列中,有多少个 t 字符串 [0,j] 区间内的⼦串。
- 状态转移方程:当s[i] = t[j]时,dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];当s[i] != t[j]时,dp[i][j] = dp[i - 1][j]。结果需要对 109 + 7 取模。
- 初始化:当s为空时, t 的⼦串中有⼀个空串和它⼀样,因此初始化第⼀列全部为1。
- 填表顺序:从上往下,从左往右。
- 返回值:返回dp[m][n]。
4.代码如下:
class Solution
{
public:
const int MOD = 1e9 + 7;
int numDistinct(string s, string t)
{
int m = s.size(), n = t.size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
for (int i = 0; i <= m; ++i)
dp[i][0] = 1;
for (int j = 1; j <= n; ++j)
{
for (int i = j; i <= m; ++i)
{
if (s[i - 1] == t[j - 1])
dp[i][j] = (dp[i - 1][j - 1] + dp[i - 1][j]) % MOD;
else
dp[i][j] = dp[i - 1][j] % MOD;
}
}
return dp[m][n];
}
};
3. 通配符匹配
1.题目链接:通配符匹配
2.题目描述:
给你一个输入字符串 ( s ) 和一个字符模式 ( p ) ,请你实现一个支持 ‘?’ 和 ‘*’ 匹配规则的通配符匹配:
‘?’ 可以匹配任何单个字符。
‘*’ 可以匹配任意字符序列(包括空字符序列)。
判定匹配成功的充要条件是:字符模式必须能够 完全匹配 输入字符串(而不是部分匹配)。
示例 1:
输入:s = “aa”, p = “a”
输出:false
解释:“a” 无法匹配 “aa” 整个字符串。
示例 2:
输入:s = “aa”, p = ""
输出:true
解释:'’ 可以匹配任意字符串。
示例 3:
输入:s = “cb”, p = “?a”
输出:false
解释:‘?’ 可以匹配 ‘c’, 但第二个 ‘a’ 无法匹配 ‘b’。
提示:
0 <= s.length, p.length <= 2000
s 仅由小写英文字母组成
p 仅由小写英文字母、‘?’ 或 ‘*’ 组成
3.问题分析:这道题用p字符串来遍历s字符串,其中p中含有 ’ ? ’ 和 ’ * ’ ,‘?’ 可以匹配任何单个字符。‘*’ 可以匹配任意字符序列(包括空字符序列),? 不能匹配空字符,所以可以将 ?当做一个万能字母,是需要占位的。
- 因为要对两个字符串进行分析,两个for循环可以将所有情况都遍历到,所以定义一个二维dp表,
dp[i][j] 表⽰: p 字符串 [0, j] 区间内的⼦串能否匹配字符串 s 的 [0, i] 区间内的⼦串。 - 状态转移方程:对符合条件的情况进行分析,其中有两大方向,一是当s[i] = p[j]或者p[i] = ‘?’,因为当s[i] = p[j]或者p[i] = '?'时,p[j]都能与s[i]进行匹配,然后只要s中0到 i - 1 与p中0到 j - 1 都匹配,那么s和p就可以匹配成功,因此当s[i] = p[j]或者p[i] = ‘?’,
dp[i][j] = dp[i - 1][j - 1];二是当p[j] = '*‘时,这种情况需要单独分析,因为’*‘可以匹配0个或多个字符,对s[i]位置以及p[j]进行分析,如果 j 位置的’*'匹配s中的空串,那么只要p(0, j - 1)与s(0, i)匹配即可,如果匹配一个、两个、三个…呢?那么就是p(0, j - 1)与s(0, i - 1)、p(0, j - 1)与s(0, i - 2)、p(0, j - 1)与s(0, i - 3) 等等,所以这里需要一个for循环来确定s中的某一个位置(只能由后往前遍历)到p[j - 1]是否匹配。因此dp[i][j] = dp[i][j - 1] || dp[i - 1][j - 1] || dp[i - 2][j - 1] || dp[i - 3][j - 1]… 这个表达式可以化简一下,对于dp中的i来说,每个位置的i为(i,i,i - 1,i - 2,i - 3…),而j为(j,j - 1,j - 1,j - 1…)要是给所有的j都减1,那么会构成新的项j - 2,如果给所有的 i 都减1,那么不会构成新项如(i,i - 1,i - 2,i - 3,i - 4…)看如下两个表达式dp[i][j] = dp[i][j - 1] ||dp[i - 1][j - 1] || dp[i - 2][j - 1] || dp[i - 3][j - 1]......给所有的 i - 1,dp[i - 1][j] =dp[i - 1][j - 1] || dp[i - 2][j - 1] || dp[i - 3][j - 1] || dp[i - 4][j - 1]......,红色字体所标识的表达式是相等的,因此dp[i][j] = dp[i][j - 1] || dp[i - 1][j]。 - 初始化:因为求dp i,j 位置的值需要知道 dp 的 i - 1,j - 1位置,以防越界,可以增加一行,一列;增加一行一列后需要对新增的一行一列初始化,对于第一列来说,只有当s,p都为空,即只有dp[0][0] = true,对于第一行来说,s是空串,而只有当p为 ‘*’ 时,p才能匹配空串,dp值才为true,要是有一个不为’*',那么之后的dp值为false。
- 填表顺序:从上到下,从左往右依次填写。
- 返回值:返回dp[m][n]的bool值即可。
4.代码如下:
lass Solution
{
public:
bool isMatch(string s, string p)
{
int m = s.size(), n = p.size();
vector<vector<bool>> dp(m + 1, vector<bool>(n + 1));
dp[0][0] = true; //初始化第一列
for (int j = 1; j <= n; ++j) //初始化第一行
{
if (p[j - 1] == '*')
dp[0][j] = true;
else
break;
}
for (int i = 1; i <= m; ++i)
{
for (int j = 1; j <= n; ++j)
{
if (s[i - 1] == p[j - 1] || p[j - 1] == '?')
dp[i][j] = dp[i - 1][j - 1];
if (p[j - 1] == '*') //因为新增一行一列,所以s,p对应的i,j应-1
{
for (int k = i; k >= 0; --k) //确定s中的某一个位置到p[j - 1]是否匹配
{
if (dp[k][j - 1])
{
dp[i][j] = true;
break;
}
}
}
}
}
return dp[m][n];
}
};
//化简后
class Solution
{
public:
bool isMatch(string s, string p)
{
int m = s.size(), n = p.size();
vector<vector<bool>> dp(m + 1, vector<bool>(n + 1));
dp[0][0] = true; //初始化第一列
for (int j = 1; j <= n; ++j) //初始化第一行
{
if (p[j - 1] == '*')
dp[0][j] = true;
else
break;
}
for (int i = 1; i <= m; ++i)
{
for (int j = 1; j <= n; ++j)
{
if (s[i - 1] == p[j - 1] || p[j - 1] == '?')
dp[i][j] = dp[i - 1][j - 1];
if (p[j - 1] == '*') //因为新增一行一列,所以s,p对应的i,j应-1
{
dp[i][j] = dp[i][j - 1] || dp[i - 1][j];
}
}
}
return dp[m][n];
}
};
4. 交错字符串
1.题目链接:交错字符串
2.题目描述:
给定三个字符串 s1、s2、s3,请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。
两个字符串 s 和 t 交错 的定义与过程如下,其中每个字符串都会被分割成若干 非空 子字符串:
s = s1 + s2 + … + sn
t = t1 + t2 + … + tm
|n - m| <= 1 交错 是 s1 + t1 + s2 + t2 + s3 + t3 + … 或者 t1 + s1 + t2 + s2 + t3 + s3 + …
注意:a + b 意味着字符串 a 和 b 连接。
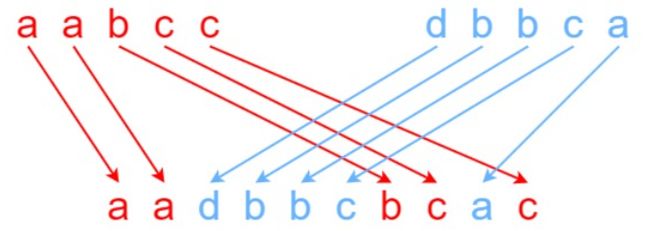
示例1:
示例 2:
输入:s1 = “aabcc”, s2 = “dbbca”, s3 = “aadbbbaccc”
输出:false
示例 3:
输入:s1 = “”, s2 = “”, s3 = “”
输出:true
提示:
0 <= s1.length, s2.length <= 100
0 <= s3.length <= 200
s1、s2、和 s3 都由小写英文字母组成
3.题目分析:
- 状态表示:和上述几道类似,
dp[i][j] 表⽰字符串 s1 中 [1, i] 区间内的字符串以及 s2 中 [1, j] 区间内的字符串,能否拼接成s3中 [1, i + j] 区间内的字符串。 - 状态转移方程:题⽬中交错后的字符串为s1 + t1 + s2 + t2 + s3 + t3… ,看似⼀个 s ⼀个 t 。实际上 s1 能够拆分成更⼩的⼀个字符,进⽽可以细化成s1 + s2 +s3 + t1 + t2 + s4… 。也就是说,并不是前⼀个⽤了s 的⼦串,后⼀个必须要⽤t 的⼦串。1.当 s3[i + j] = s1[i] 的时候,说明交错后的字符串的最后⼀个字符和s1 的最后⼀个字符匹配了。那么整个字符串能否交错组成,变成:s1中[1, i - 1]区间上的字符串以及s2中[1, j]区间上的字符串,能够交错形成s3 中 [1, i + j - 1] 区间上的字符串,也就是 dp[i - 1][j] ,此时dp[i][j] = dp[i - 1][j] 。2.当 s3[i + j] = s2[j] 的时候,与第一种情况类似,只要s1中的[1,i]区间和s2中的[1, j - 1] 区间能拼接s3[1, i + j - 1] 即可,此时dp[i][j] = dp[i][j - 1],所以状态转移方程为:
如果s1[i] = s3[i + j],dp[i][j] = dp[i - 1][j];如果s2[j] = s3[i + j],dp[i][j] = dp[i][j - 1]。 - 初始化:因为求dp i,j 位置的值需要知道 dp 的 i - 1,j - 1位置,所以对第一行和第一列初始化即可;第一行表示s1为空串,所以只考虑s2即可,相反第一列表示s2为空串,所以只考虑s1即可。
- 填表顺序:从上到下,从左往右依次填写。
- 返回值:返回dp[m][n]的bool值即可。
4.代码如下:
class Solution
{
public:
bool isInterleave(string s1, string s2, string s3)
{
int m = s1.size(), n = s2.size();
if (m + n != s3.size())
return false;
vector<vector<bool>> dp(m + 1, vector<bool>(n + 1));
dp[0][0] = true;
for (int i = 1; i <= m; ++i)
{
if (s1[i - 1] == s3[i - 1])
dp[i][0] = true;
else
break;
}
for (int j = 1; j <= n; ++j)
{
if (s2[j - 1] == s3[j - 1])
dp[0][j] = true;
else
break;
}
for (int i = 1; i <= m; ++i)
{
for (int j = 1; j <= n; ++j)
{
if (s1[i - 1] == s3[i + j - 1])
dp[i][j] = dp[i - 1][j];
if (s2[j - 1] == s3[i + j - 1])
dp[i][j] = dp[i][j] || dp[i][j - 1];
}
}
return dp[m][n];
}
};