算法通关村第十七关——贪心其实很简单(青铜)
算法通关村第十七关——贪心其实很简单(青铜)
-
- 1 难以解释的贪心算法
-
- 1.1 什么是贪心
- 1.2 常见使用场景
- 2 贪心问题举例
-
- 2.1 分发饼干
- 2.2 柠檬找水
- 2.3 分发糖果
1 难以解释的贪心算法
1.1 什么是贪心
贪心的本质是选择每一阶段的局部最优,从而达到全局最优。
那贪心是否一定能得到最优解呢?《算法导论》给出了最明确的答案——贪心算法不能保证一定能得到最优解,但是对很多问题确实可以得到最优解 。
既然不能保证 ,我怎么知道某个解法是不是最优解呢?很遗憾,笔者查阅大量材料,也没有谁给出定论,大部分的解释其实就是——看上去是就是了。
那我怎么知道什么时候该用贪心呢?这要求要解决的问题具有”最优子结构“,那什么是”最优子结构“呢?这个问题好比用高等数学证明”1+1=2“,解释不如不解释。
1.2 常见使用场景
贪心常见的经典应用场景有如下这些,这些算法很多与图有关,本身比较复杂,也难以实现 ,我们一般掌握其思想即可:
1.排序问题:选择排序、拓扑排序 2.优先队列:堆排序 3.赫夫曼压缩编码 4.图里的Prim、Fruskal和Dijkstra算法 5.硬币找零问题 6.分数背包问题 7.并查集的按大小或者高度合并问题或者排名 8.任务调度部分场景 9.一些复杂问题的近似算法
在力扣中,常见的贪心算法有以下几种:
- 零钱兑换(Coin Change)问题:给定一些不同面额的硬币和一个总金额,计算出能够凑成总金额所需的最少硬币数量。leetcode 322. 零钱兑换
- 买卖股票的最佳时机(Best Time to Buy and Sell Stock)问题:给定一个数组,表示每天的股票价格,计算出在最低价买入,最高价卖出的情况下能够获得的最大利润。leetcode 121. 买卖股票的最佳时机
- 分发饼干(Assign Cookies)问题:给定两个数组,分别表示孩子的胃口和每个饼干的大小,计算出最多能够满足的孩子数量。leetcode 455. 分发饼干
- 跳跃游戏(Jump Game)问题:给定一个非负整数数组,表示每个位置上的最大跳跃步数,判断是否能够到达最后一个位置。leetcode 55. 跳跃游戏
- 加油站(Gas Station)问题:给定两个数组,分别表示每个加油站的汽油量和到下一个加油站的距离,计算出从某个加油站出发,能够绕一圈回到原点的加油站的索引。leetcode 134. 加油站
2 贪心问题举例
2.1 分发饼干
455. 分发饼干
思路:
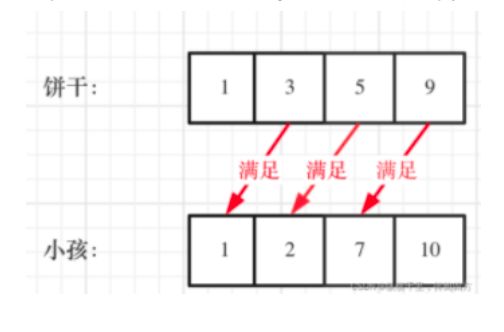
为了满足更多的小孩,就不要造成饼干尺寸的浪费。
大尺寸的饼干既可以满足胃口大的孩子也可以满足胃口小的孩子,那么就应该优先满足胃口大的。
这里的局部最优就是大饼干喂给胃口大的,充分利用饼干尺寸喂饱一个,全局最优就是喂饱尽可能多的小孩。
可以尝试使用贪心策略,先将饼干数组和小孩数组排序。
然后从后向前遍历小孩数组,用大饼干优先满足胃口大的,并统计满足小孩数量。
如图:
代码:
class Solution {
// 思路1:优先考虑饼干,小饼干先喂饱小胃口
public int findContentChildren(int[] g, int[] s) {
Arrays.sort(g);
Arrays.sort(s);
int start = 0;
int count = 0;
for (int i = 0; i < s.length && start < g.length; i++) {
if (s[i] >= g[start]) {
start++;
count++;
}
}
return count;
}
}
class Solution {
// 思路2:优先考虑胃口,先喂饱大胃口
public int findContentChildren(int[] g, int[] s) {
Arrays.sort(g);
Arrays.sort(s);
int count = 0;
int start = s.length - 1;
// 遍历胃口
for (int index = g.length - 1; index >= 0; index--) {
if(start >= 0 && g[index] <= s[start]) {
start--;
count++;
}
}
return count;
}
}
2.2 柠檬找水
leetcode 860. 柠檬水找零
这个题描述有点啰嗦,但是根据示例,不难看懂。这个题给小学生是不是也会做呢?然后当我们分析如何用代码实现时会有点懵,其实主要有三种情况:
-
如果给的是5,那么直接收下。
-
如果给的是10元,那么收下一个10,给出一个5,此时必须要有一个5才行。
-
如果给的是20,那么优先消耗一个10元,再给一个5元。假如没有10元,则给出3个5元。
上面情况三里,有10就先给10,没有才给多个5,这就是贪心选择的过程。为什么要优先消耗一个10和一个5呢?小学生都知道因为10只能给账单20找零,而5可以给账单10和账单20找零,5更万能!所以这里的局部最优就是遇到账单20,优先消耗美元10,完成本次找零。
class Solution {
public boolean lemonadeChange(int[] bills) {
if(bills[0] > 5){
return false;
}
int money1 = 0, money2 = 0;
for(int i=0; i < bills.length; i++){
if(bills[i] == 5){
money1++;
}
if(bills[i] == 10){
money1--;
money2++;
}
if(bills[i] == 20){
if(money2 > 0){
money1--;
money2--;
}else{
money1 -= 3;
}
}
if(money1 < 0 || money2 < 0) return false;
}
return true;
}
}
2.3 分发糖果
题目链接:leetcode 135. 分发糖果
学习链接:代码随想录 贪心 分发糖果
思路:
由题意可得两个要求:
-
每个孩子至少分配到 1 个糖果。
-
相邻两个孩子评分更高的孩子会获得更多的糖果。
则:这道题目一定是要确定一边之后,再确定另一边,例如比较每一个孩子的左边,然后再比较右边,如果两边一起考虑一定会顾此失彼。
所以:
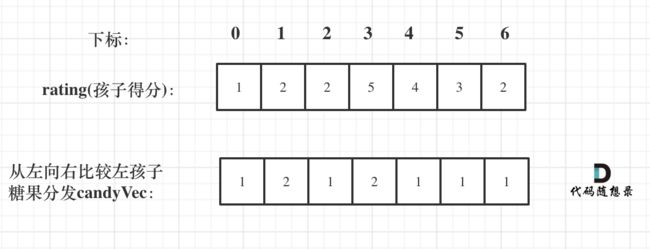
局部最优解,只要右边评分比左边大,右边的孩子就多一个糖果
if (ratings[i] > ratings[i - 1]) candyVec[i] = candyVec[i - 1] + 1;
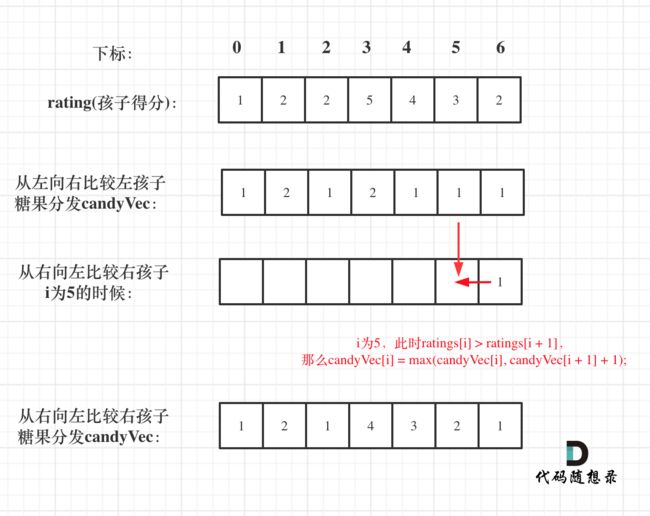
再确定左孩子大于右孩子的情况(从后向前遍历)
局部最优解:取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量,candyVec[i]只有取最大的才能既保持对左边candyVec[i - 1]的糖果多,也比右边candyVec[i + 1]的糖果多。
candyVec[i] = Math.max(candyVec[i], candyVec[i + 1] + 1);
则,代码:
class Solution {
public int candy(int[] ratings) {
int len = ratings.length;
int[] candyVec = new int[len];
candyVec[0] = 1; // 第一个人至少得到一个糖果
// 从左往右遍历,保证每个人满足第一个条件
for(int i=1; i<len; i++){
candyVec[i] = ratings[i] > ratings[i-1] ? candyVec[i-1] + 1 : 1;
}
// 从右往左遍历,保证每个人满足第二个条件
for(int i = len - 1 - 1; i>=0; i--){
if(ratings[i] > ratings[i+1]){
candyVec[i] = Math.max(candyVec[i], candyVec[i+1] + 1);
}
}
int ans = 0;
for(int num : candyVec){
ans += num;
}
return ans; // 返回所有人的糖果总数
}
}
over~~