【数字图像处理笔记】01-数字图像基础

01-数字图像基础

1. 图像类型

   1. 黑白(二值)图像

      只有黑白两种颜色的图像称为黑白图像或单色图像，图像的每个像素只能是黑或白，没有中间的过渡，故又称为二值图像。
      二值图像的像素值只能为0或1，图像中的每个像素值用1位存储。图像矩阵中用1表示白色，0表示黑色。
      

   2. 灰色图像

      在灰度图像中，像素灰度级用8位表示，所以每个像素都是介于黑色和白色之间的256（2^8=256）种灰度中的一种，灰度图像只有从黑到白的256种灰度色域而没有彩色。灰度取值范围为0～255，“0表示纯黑色，“255”表示纯白色，中间的数字表示黑白之间的过渡色。灰度值越小，图像颜色越黑，灰度值越大，图像颜色越白。

      

   3. 彩色图像

      ​ 彩色图像除有亮度信息外，还包含有颜色信息。彩色图像的表示与所采用的彩色空间，即彩色模型有关，同一幅彩色图像如果采用不同的彩色空间表示，则对其的描述可能会有很大的不同。常用的表示方法主要有真彩色图像和索引图像。
      ​ 真彩色图像又称为24位彩色图像。在真彩色图像中，每个像素由红、绿、蓝3个字节组成，每个字节为8位，表示0～255不同的亮度值。这3个字节的组合，可以产生1670万种不同的颜色。由于它所表达的颜色远远超出了人眼所能辨别的范围，故将其称为“真彩色”。

      ​ 在真彩色出现之前，由于技术上的原因，计算机在处理时并没有达到每个像素24位的真彩色水平，为此人们创造了索引颜色。**索引图像既包括存放图像数据的二维矩阵，还包括一个颜色索引矩阵（称为MAP），又称为映射图像。MAP矩阵也可以由二维数组表示，矩阵大小由存放图像的矩阵元素的灰度值范围决定。**若矩阵元素灰度值范围为0～255，则MAP矩阵的大小为256×3，矩阵的三列分别为R、G、B值。图像矩阵的每一个灰度值对应于MAP中的一行，例如，某一像素的灰度值为64，则表示该像素与MAP矩阵的第64行建立了映射关系，该像素在屏幕上的显示颜色由MAP矩阵第64行的R、G、B叠加而成。

      

2. 图像的统计特性

   ​ f(i,j)表示大小为M*N的数字图像

   1. 图像熵

      一幅图像如果共有个灰度值，并且各灰度值出现的概率分别为p1,p2,pk,根据香农定理，图像的平均信息量可以表示为：
      $$H=-\sum _{i=1}^k{p}_{i}lo{g}_2(p_i)$$
      H称为信息熵，当图像中的各灰度值出现的概率彼此相等时，图像的熵最大，对于一幅采用8bit表示的数字图像，则信息熵的为：
      $$H=-\sum _{i=0}^{255}{p}_{i}lo{g}_2(p_i)$$

      clc;clear;close all;
      
      I=imread('lena.jpg'); %  I数组大小 512x512
      imshow(I);title('Lena');
      img_entropy=entropy(I); %image_mean求出图像的信息熵
      disp(['img_entropy=',num2str(img_entropy)]);
      
      
      % 计算图像的信息熵
      % img为图像读入的矩阵，img_entropy返回值图像的信息熵
      function img_entropy=entropy(img)
          img=double(img);
          [M,N]=size(img);
          img=transpose(img(:));
          T=zeros(1,256);
          
          for i=1:256
              T(i)=sum(img==(i-1));
              T(i)=T(i)/(M*N);
          end
          img_entropy=-T(T>0)*transpose(log2(T(T>0)));
      end
      

   2. 图像灰度平均值

      灰度平均值是指一幅图像中所有的像素灰度值的算术平均值，根据算术平均值定义，灰度平均值计算公式如下：

      图像的灰度平均值反映了图像在物体不同部分的平均反射强度。
      $$\overline{f}=\frac{{\sum }_{i=0}^{M-1}{\sum }_{i=0}^{N-1}f(i,j)}{MN}$$

      function [result]=image_mean(img)
      %img为图像读入的矩阵，result返回的是这些数求得的均值
      	img=double(img);%影像矩阵的类型默认是uint8 （0~255） 如果不转换为double，在求和时会溢出
      	img=img(:);%将影像变为n行一列，采用单层循环就可以计算，加快计算速度
      	sum=0;%用于求和
      	for i=1:size(img,1)
          	sum=sum+img(i);%求出矩阵中所有数之和
      	end
      	result=sum/size(img,1);%求出均值
      end
      

      clc;clear;close all;
      
      % imread读取图片 imshow展示图片 %image_mean求出图像矩阵所有数值的均值
      I=imread('lena.jpg'); %  I数组大小 512x512
      imshow(I);title('Lena');
      image_mean=image_mean(I); 
      disp(image_mean);
      disp(['image_mean=',num2str(image_mean)]);
      

      在Matlab中，采用函数mean2()计算矩阵的均值。

      对于灰度图像，图像数据是二维矩阵，可以通过函数mean2()计算图像的平均灰度值。

      对于RGB彩色图像数据P，mean2()所有颜色值的平均值。如果要计算RGB彩色图像每种颜色的平均值，例如，红色的平均值，可
      以采用mean2(P(:,:,1))。

      clc;clear;close all;
      %leaa.jpg 灰色图像  %leaa.png 彩色图像 
      rgb_img  = imread('lena.png'); %  数组大小 512x512 
      gray_img = imread('lena.jpg'); %  数组大小 512x512 
      gray = mean2(gray_img); %灰度图像均值
      rgb  = mean2(rgb_img); %RGB图像均值
      disp(['gray_img_mean=',num2str(gray)]);
      disp(['rgb_img_mean=',num2str(rgb)]);
      
      r_mean = mean2(rgb_img(:,:,1));
      g_mean = mean2(rgb_img(:,:,2));
      b_mean = mean2(rgb_img(:,:,3));
      disp(['RGB图像 r_mean=',num2str(r_mean)]);
      disp(['RGB图像 g_mean=',num2str(g_mean)]);
      disp(['RGB图像 b_mean=',num2str(b_mean)]);
      

      注意点：
      ①图像矩阵的每个值都是uint8类型的，uint8的范围是0-255，在进行求和之前需要把图像矩阵转换成double类型，如果不转换，继续对uint8类型进行运算会产生溢出；
      ②将矩阵变为1×n或者n×1形式，求和时可以采用单层循环，加快计算速度。

   3. 图像灰度众数

      图像灰度众数是指图像中出现次数最大的灰度值，其物理意义是指一幅图像中面积占优的物体的灰度值信息。

      clc;clear;close all;
      
      % imread读取图片 imshow展示图片 %image_mode求出图像矩阵的众数
      I=imread('lena.jpg'); %  I数组大小 512x512
      imshow(I);title('Lena');
      image_mode=img_mode(I); 
      disp(['image_mode=',num2str(image_mode)]);
      

      function [result]=img_mode(img)
      %img为图像读入的矩阵，result返回的是众数的数组
      	img=img(:);
      	h=zeros(1,256);%定义一个数组用来几率每个数值出现的次数
      for i=1:size(img,1)
          h(img(i)+1)=h(img(i)+1)+1;%由于矩阵的值时0-255，所以加一以后才是索引值
      end
      	ma=h(1);
      for i=1:256
      %求出现的最大次数
          if(h(i)>ma)
              ma=h(i);
          end
      end
      	j=1;
      for i=1:256
      %得到所有出现次数最多的数
          if(ma==h(i))
             num(j)=i;
             j=j+1;
          end
      end
      	result=num;
      end
          
      
      

      注意点：
      ①众数可能有多个，在有多个众数的情况下不能只返回一个；
      ②我们读入的数组矩阵的数值范围是0-255。

   4. 图像灰度中位数

      图像灰度中值是指数字图像全部灰度级中处于中间的值(按照排序)，当灰度级数为偶数时，则取中间的两个灰度值的平均值。

      例如，若某一图像全部灰度级如下：188,176,171,166,160则灰度中值为171。

   5. 图像灰度方差

      灰度方差反映各像素灰度值与图像平均灰度值的离散程度，计算公式如式：
      $$S=\frac{{\sum }_{i=0}^{M-1}{\sum }_{i=0}^{N-1}[f(i,j)-\overline{f}{]}^2}{MN}$$
      与图像信息熵类似**，图像灰度方差同样是衡量图像信息量大小的主要度量指标**，是图像统计特性中最重要的统计量之一，方差越大，图像的信息量越大。

      图像的标准差

      对于向量来说，标准差s:
      $$s=\sqrt{\frac{1}{n-1}\sum _{i=1}^n(x_i-x{)}^2}$$
      其中x为向量的平均值
      $$x=\frac{1}{n}\sum _{i=1}^n{x}_i$$
      在Matlab中，std()计算向量的标准差，std2()计算矩阵的标准差。

      clc;clear;close all;
      
      % imread读取图片 imshow展示图片 %img_variance灰度图像方差
      I=imread('lena.jpg'); %  I数组大小 512x512
      % 默认输入图像为灰色图像，如果不是需要将图像灰度化 
      %I = rgb2gray(I);
      imshow(I);title('Lena');
      image_var=img_variance(I); 
      disp(['image_var=',num2str(image_var)]);
      
      s1 = std2(I); %计算原图像标准差
      disp(['s1 img_var=',num2str(s1)]);
      img_var = s1^2;
      disp(['img_var=',num2str(img_var)]);
      J = histeq(I);%图像直方图均衡化
      s2 = std2(J); %计算均衡化的图像标准差
      disp(['s2 img_var=',num2str(s2)]);
      

      自定义函数

      function [ result ] = img_variance(img)
      %img灰度图像数组 
      	img=img(:);%把行向量变成列向量
      	img=double(img);
      	length=size(img,1);%得到a的维数
      	sum=0;
      	img_mean=image_mean(img);%均值函数
      	for i=1:length
         		sum=sum+(img(i)-img_mean)*(img(i)-img_mean);
      	end
      	result=sum/length;
      end
      
      clc;clear;close all;
      
      % imread读取图片 imshow展示图片 %img_variance灰度图像方差
      I=imread('lena.jpg'); %  I数组大小 512x512
      imshow(I);title('Lena');
      image_var=img_variance(I); 
      disp(['image_var=',num2str(image_var)]);
      

   6. 图像灰度值域

      图像的灰度值域是指图像最大灰度值fmax和最小灰度值fmin之查，计算公式如下：
      $$f_{range}(i,j)=f_{max}(i,j)-f_{min}(i,j)$$

3. 数字图像直方图

   图像直方图描述了一张图片像素值分布的情况，我们知道，例如对于一张sRGB图像，我们可以看作是一个HW1的矩阵，矩阵中每个元素的取值范围为[0,255],图像直方图h(g)定义为像素值为g的元素的个数。同理，彩色图像中，需要计算每个通道的图像直方图。

   

   灰度直方图

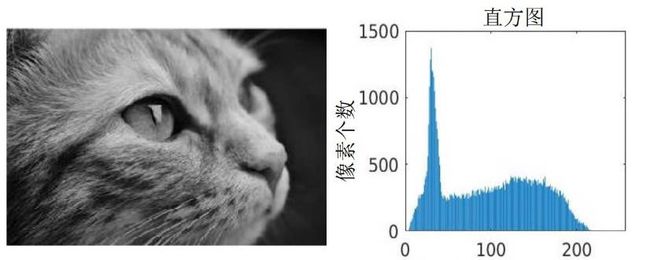
   灰度直方图是灰度级的函数，描述的是图像中具有该灰度级的像元的个数。确定图像像元的灰度值范围，以适当的灰度间隔为单位将其划分为若干等级，以横轴表示灰度级，以纵轴表示每一灰度级具有的像元数或该像元数占总像元数的比例值，做出的条形统计图即为灰度直方图。

   如下图所示，做直方图的过程：

直方图的性质：

1. 直方图反映了图像中的灰度分布规律。它描述每个灰度级具有的像元个数，但不包含这些像元在图像中的位置信息。
2. 任何一幅特定的图像都有唯一的直方图与之对应，但不同的图像可以有相同的直方图。
3. 如果一幅图像有两个不相连的区域组成，并且每个区域的直方图已知，则整幅图像的直方图是该两个区域的直方图之和

直方图的应用：

1. 对于每幅图像都可做出其灰度直方图。
2. 根据直方图的形态可以大致推断图像质量的好坏。由于图像包含有大量的像元，其像元灰度值的分布应符合概率统计分布规律。假定像元的灰度值是随机分布的，那么其直方图应该是正态分布。
3. 图像的灰度值是离散变量，因此直方图表示的是离散的概率分布。若以各灰度级的像元数占总像元数的比例值为纵坐标轴做出图像的直方图，将直方图中各条形的最高点连成一条外轮廓线，纵坐标的比例值即为某灰度级出现的概率密度，轮廓线可近似看成图像相应的连续函数的概率分布曲线。

灰色图像直方图Matlab代码实现 （在图像加密中，灰色直方图是一个重要的可视化分析指标）

clc;clear;close all;
% imread读取图片   imshow展示图片
% imhist直方图   histeq直方图均衡化
I=imread('lena.jpg');
subplot(2,2,1);imshow(I);title('原始图像')
subplot(2,2,2);imhist(I);title('直方图')
J=histeq(I);
subplot(2,2,3);imshow(J);title('直方图均衡化');
subplot(2,2,4);imhist(J);title('直方图');

4. 多维度图像的统计特性

   数字图像处理中，一幅RGB图像包含了三个波段的灰度图像。

   对于多维度图像处理，不仅要考虑单个维度图像的统计特性，还应考虑各个维度间存在的关联特性。图像维度之间的关联特性不仅是图像分析的重要参数，而且也是图像彩色合成方案的主要依据之一。在图像加密中，图像之间的关联特性是一个重要的指标。

   统计特性包括：协方差 相关系数

   协方差

   设f(i,j)和g(i,j)表示大小为M*N的两幅图像，则两者之间的协方差计算公式如下：

   其中N个维度的相互之间的协方差矩阵如下：
   ∑ = ( S 11 2 S 12 2 . . . S 1 N 2 S 11 2 S 12 2 . . . S 1 N 2 . . . . . . . . . . . . S N 1 2 S N 2 2 . . . S N N 2 ) \sum = \begin{pmatrix} S_{11}^{2}& S_{12}^{2}& ...& S_{1N}^{2}\\ S_{11}^{2}& S_{12}^{2}& ...& S_{1N}^{2}\\ ...& ...& ...& ...\\ S_{N1}^{2}& S_{N2}^{2}& ...& S_{NN}^{2} \end{pmatrix} ∑= ​S112​S112​...SN12​​S122​S122​...SN22​​............​S1N2​S1N2​...SNN2​​ ​

   $$S_{gf}^2=S_{fg}^2=\frac{1}{MN}\sum _{i=0}^{M-1}\sum _{j=0}^{N-1}\left[f(i,j)-\overline{f}\right]\left[g(i,j)-\overline{g}\right]$$

   clc;clear;close all;
   
   % imread读取图片 imshow展示图片 %img_variance灰度图像协方差
   I1=imread('lena.jpg'); %  I数组大小 512x512
   I2=imread('lena.jpg'); %  I数组大小 512x512
   % 默认输入图像为灰色图像，如果不是需要将图像灰度化 
   %I = rgb2gray(I);
   subplot(1,2,1);imshow(I1);title('Lena');
   subplot(1,2,2);imshow(I2);title('mandril');
   image_cov=img_cov(I1,I2); 
   disp(['image_cov=',num2str(image_cov)]);
   
   function [ result ] = img_cov(img_a,img_b)
   %a,b分布为两张不同的图像
   	img_a=img_a(:);
   	img_b=img_b(:);
   	img_a=double(img_a);
   	img_b=double(img_b);
       
   	mi1=image_mean(img_a);
   	mi2=image_mean(img_b);
       
   	sum=0;
       for i=1:size(img_a,1)
           sum=sum+(img_a(i)-mi1)*(img_b(i)-mi2);
       end
       
   	result=sum/size(img_a,1);
   end
   
   
   

   相关系数

   数字图像处理中的相关系数反映了两个不同维度图像所含信息的重叠程度，它是表示图像不同维度间相关程度的统计量。如果两个维度间的相关系数较大，则表示两个维度具有较高的相关性，一个维度与其本身的相关系数为1，表明相关程度达到最大值。当相关系数非常大时，仅选择其中的一个维度就可以表示两个维度的信息。相关系数表达式如下。

   Cov(f,g)为图像f(i,j),g(i,j)的协方差，dff为图像f(i,j)标准差，dgg为图像g(i,j)标准差.
   $$\frac{Co{v}_{fg}}{d_{ff}{d}_{gg}}$$

   $$Co{v}_{fg}=\sum _m\sum _n(f-\overline{f})(g-\overline{g})$$

   $$d_{ff}=\sqrt{\sum _m\sum _n(f-\overline{f}{)}^2}$$

   $$d_{gg}=\sqrt{\sum _m\sum _n(g-\overline{g}{)}^2}$$

   N个维度的相关系数矩阵如下：
   R = ( 1 r 12 r 13 . . . r 1 N 2 r 21 1 r 23 . . . r 2 N 2 . . . . . . . . . . . . . . . r N 1 r N 2 r N 3 . . . 1 ) R = \begin{pmatrix} 1 & r_{12}& r_{13}& ...& r_{1N}^{2}\\ r_{21}& 1& r_{23}& ...& r_{2N}^{2}\\ ...& ...& ...& ...& ...\\ r_{N1}& r_{N2}& r_{N3}& ...& 1 \end{pmatrix} R= ​1r21​...rN1​​r12​1...rN2​​r13​r23​...rN3​​............​r1N2​r2N2​...1​ ​
   Matlab 代码实现

   function [ result ] = img_correlation(img_a,img_b )
   %a,b分布为两张不同的图像
   	img_a=img_a(:);
   	img_b=img_b(:);
   	img_xie=img_cov(img_a,img_b);%协方差
   	img_var1=img_variance(img_a);%方差
   	img_var2=img_variance(img_b);%方差
   	result=img_xie/(sqrt(img_var1)*sqrt(img_var2));
   end
   
   
   clc;clear;close all;
   
   % imread读取图片 imshow展示图片 %image_corr相关系数
   I1=imread('lena.jpg'); %  I数组大小 512x512
   I2=imread('mandril.tif'); %  I数组大小 512x512
   % 默认输入图像为灰色图像，如果不是需要将图像灰度化 
   %I = rgb2gray(I);
   figure
   subplot(1,2,1);imshow(I1);title('Lena');
   subplot(1,2,2);imshow(I2);title('Mandril');
   image_corr=img_correlation(I1,I2); 
   disp(['image_corr=',num2str(image_corr)]);
   
   J1 = medfilt2(I1);%对灰色图像I1进行中值滤波
   r_corr = corr2(I1,J1);
   disp(['r_corr=',num2str(r_corr)]);
   figure
   subplot(1,2,1);imshow(I1);
   subplot(1,2,2);imshow(J1);
   
   

5. 图像类型转换