6 机器学习 IV与WOE 分箱 过抽样与欠抽样
机器学习
1 IV与WOE
1.1 IV
IV,Information Value,指的是信息价值或者信息量。
IV可以理解为特征筛选的量化指标, 用于衡量数据特征的预测能力或者在模型预测过程中对预测结果的影响程度。
关于衡量特征预测能力的理解
假设在一个分类问题中,数据集分为两种标签类别:Y1和Y2。对于一个待预测的样本A,要判断其属于类别Y1还是类别Y2,我们需要一定的信息,假设这个信息总量是I,而这些信息蕴含在待预测样本的所有特征C1,C2,…,Cn中。对于某个特征Ci,如果特征Ci包含的信息越多,那么它对于判断样本A的类别这个问题的贡献就越大,即特征Ci的信息价值就越大,等价于特征Ci的IV就越大,因此特征Ci就越应该优先选择出来并用于训练模型。
1.2 WOE介绍及计算公式
WOE,Weight of Evidence,指的是证据权重,WOE是对原始特征的一种编码形式。要对一个特征进行WOE编码,首先需要对这个变量进行分组处理,分组处理也称为离散化、分箱等。
WOE的计算公式
对于分组后的第i组
W O E i = l n ( P y i P n i ) = l n ( # y i / # y t # n i / # n t ) WOE_i = ln({{P_{y_i}} \over {P_{n_i}}}) = ln({{\# y_i / \# y_t} \over {\# n_i / \# n_t}}) WOEi=ln(PniPyi)=ln(#ni/#nt#yi/#yt)
P y i P_{y_i} Pyi表示组中正例样本数量占全部正例样本数量的比例;
P n i P_{n_i} Pni表示组中负例样本数量占全部负例样本数量的比例;
# y i \# y_i #yi表示组中正例样本数量, # y t \# y_t #yt表示全部正例样本数量;
# n i \# n_i #ni表示组中负例样本数量, # n t \# n_t #nt表示全部负例样本数量。
从公式中可以看出,WOE实际上表示
“指定组中正例样本数量占样本集中所有正例样本数量的比例”与“当前组中负例样本数量占样本集中所有负例样本数量的比例”之间的差异。
对于分组后的第i组,
W O E i = l n ( # y i / # y t # n i / # n t ) = l n ( # y i / # n i # y t / # n t ) WOE_i = ln({{\# y_i / \# y_t} \over {\# n_i / \# n_t}}) = ln({{\# y_i / \# n_i} \over {\# y_t / \# n_t}}) WOEi=ln(#ni/#nt#yi/#yt)=ln(#yt/#nt#yi/#ni)
- 对于给定的样本集, # y t / # n t {\# y_t / \# n_t} #yt/#nt 是固定值,因此WOE也可以反映出指定组中正例样本数量与负例样本数量的比值。WOE越大,这个组的正例样本占比就越大。
- WOE值可正可负,每一组的WOE值的正负由当前组中正例样本数量与负例样本数量的比例,与样本整体中正例样本数量与负例样本数量的比例的大小关系决定。
如果某一组的WOE值为正,与整体数据相比这个组更偏向于将样本划分到正例样本中,反之,如果某一组的WOE值为负,与整体数据相比这个组更偏向于将样本划分到负例样本中。 - 如果某一组的WOE值为0,则说明这个组中正负例样本数量的比例与整体情况相同。
1.3 IV计算公式
IV的计算公式是以WOE的计算公式为基础的。
对于分组后的第i组
I V i = ( P y i − P n i ) × W O E i I V i = ( P y i − P n i ) × l n ( P y i P n i ) I V i = ( # y i / # y t − # n i / # n t ) × l n ( # y i / # y t # n i / # n t ) \begin{aligned} IV_i =& (P_{y_i} - P_{n_i}) \times WOE_i \\ IV_i =& (P_{y_i} - P_{n_i}) \times ln({{P_{y_i}} \over {P_{n_i}}}) \\ IV_i =& ({\# y_i / \# y_t} - {\# n_i / \# n_t}) \times ln({{\# y_i / \# y_t} \over {\# n_i / \# n_t}}) \end{aligned} IVi=IVi=IVi=(Pyi−Pni)×WOEi(Pyi−Pni)×ln(PniPyi)(#yi/#yt−#ni/#nt)×ln(#ni/#nt#yi/#yt)
- 从IV的计算公式可以看出,如果某一组的正例样本数量与负例样本数量的比例,与整体数据的正例样本数量与负例样本数量的比例相差越大,则这个组的IV值就越大。
- 如果某一组的正例样本数量与负例样本数量的比例,与整体数据的正例样本数量与负例样本数量的比例相等,则IV值为0。
- IV值不可能为负数。
1.4 案例
1.4.1 案例介绍
某公司准备举行一个活动,举行活动前在小范围的客户群体中进行一次试点,收集一些用户对这次活动响应,然后希望利用这些数据构造模型,并预测假如举行这次的活动,是否能够得到很好的响应。
假设从公司的客户列表中随机抽取了100000名客户进行了营销活动测试,其中响应的客户有10000个,并且已经获取了这些响应客户的一些变量(特征),作为模型的候选变量集,包括:
- 最近一个月是否存在购买行为;
- 最近一次购买的金额;
- 最近一笔购买的商品类别;
- 是否是公司的VIP客户。
假设已经对这些变量进行了离散化处理,统计结果如下所示。
(1) 最近一个月是否存在购买行为

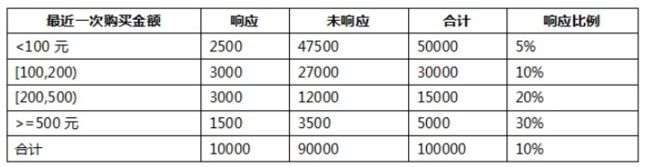
(2) 最近一次购买的金额

(3) 最近一笔购买的商品类别

(4) 是否是公司的VIP客户

1.4.2 计算WOE和IV
以最近一次的购买金额为例,将响应特征设为正例,未响应特征设为反例。
1.4.2.1 计算WOE
计算特征(最近一次的购买金额)的WOE。


将响应特征设为正例,未响应特征设为反例。
- 由上面的数据可以看出,WOE值反映了每个组内响应数据数量与未响应数据数量的占比情况。对于所有的分组,响应的比例越大,WOE值越大。
- 当某一组的WOE值为正时,与整体相比这个组的数据更偏向于响应,反之如果某一组的WOE值为负,与整体相比这个组的数据更偏向于不响应。
- 如果某一组的WOE值为0,则说明这个组的特征偏向与整体数据相同。
1.4.2.2 计算IV
1.4.3 比较IV,进行特征选择
| 特征 | IV |
|---|---|
| 最近一个月是否存在购买行为 | 0.250225 |
| 最近一次购买的金额 | 0.492706 |
| 最近一笔购买的商品类别 | 0.615276 |
| 是否是公司的VIP客户 | 1.565504 |
通过比较各个特征的IV值,发现特征(是否是公司的VIP客户)的IV值最高,说明这个特征的预测能力最强。
如果需要选择出某些特征去训练模型,则可以选择IV值较高的特征。
1.4.4 思考
进行特征选择时,为什么使用IV而不是直接使用WOE作为选择标准。
每个特征的IV和WOE都表示当前分组对这个特征的预测能力。
例如,基于某个特征A进行分组,A特征只有两个:0和1。

当特征A取1时,响应比例达到了90%,但是与另一组(A=0)相比,这个组(A=1)的样本数量在整体样本中的占比非常小,因此仅使用响应比例不能很好的进行特征选择。
与WOE相比,IV的计算公式是在WOE的基础上增加了系数( P y i − P n i P_{y_i} - P_{n_i} Pyi−Pni),这个系数中蕴含了这个分组样本在整体样本中的数量占比情况。因此,进行特征选择时,使用IV作为标准可以考虑到每个分组的样本数量的占比情况,更加严谨。
2 分箱
2.1 介绍
数据分箱,也称为离散分箱或者分段,是一种数据预处理技术,用于将连续型特征进行离散化处理,可以将多个连续值按照取值范围分别装入有限数量的箱子中,通过分箱操作可以减少次要观察误差的影响。
例如,有一组人员年龄统计数据。
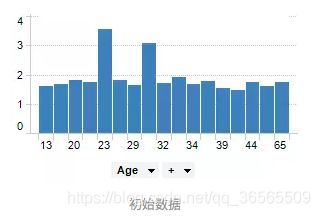
通过分箱操作,可以将每个箱子的范围扩大,将箱子的数量减少。

2.2 分箱的作用
- 分箱后易于增加或减少离散特征,易于模型的快速迭代,提升计算速度;
- 特征离散化后,模型会更稳定;
例如对用户年龄进行离散化处理后,以10年作为一个区间长度,当时间过了一年,不处于年龄区间边界的用户不会因为年龄长一岁就移动至其它区间中; - 特征离散化起到了简化模型的作用,可以适当降低了模型过拟合的风险。
2.3 代码实现
2.3.1 cut
cut根据样本数据的数值来确定箱子的均匀间隔,即每个箱子的间距尽量相等。
pd.cut(x, bins, right=True, labels=None, retbins=False, precision=3, include_lowest=False, duplicates='raise')
x - 待分箱的一维数据;
bins - 指定分隔区间;
若输入int数字则表示分箱后箱子数量;
若输入list或np.array则表示指定了每个箱子的范围,区间范围默认是左开右闭。
right - 布尔值,默认为True,表示区间范围是否包含右侧;
labels - 为分箱后的箱子设置标签,数量必须和箱子数量一致。
import numpy as np
import pandas as pd
from pandas import Series, DataFrame
score_list = np.linspace(0, 20, num=11)
print(score_list)
# [ 0. 2. 4. 6. 8. 10. 12. 14. 16. 18. 20.]
- 通过参数bins指定箱子数量。
bins = 3
score_cat = pd.cut(score_list, bins)
print(pd.value_counts(score_cat))
'''
(13.333, 20.0] 4
(-0.02, 6.667] 4
(6.667, 13.333] 3
'''
- 通过参数bins指定箱子范围。
bins=[0, 4, 8, 16, 20]
score_cat = pd.cut(score_list, bins)
print(pd.value_counts(score_cat))
'''
(8, 16] 4
(16, 20] 2
(4, 8] 2
(0, 4] 2
'''
- 通过参数labels为箱子设置标签。
bins = 3
score_cat = pd.cut(score_list, bins, labels=['A', 'B', 'C'])
print(score_cat.tolist()) # ['A', 'A', 'A', 'A', 'B', 'B', 'B', 'C', 'C', 'C', 'C']
print(pd.value_counts(score_cat))
'''
C 4
A 4
B 3
'''
2.3.2 qcut 等平分箱
qcut可以指定箱子数量,根据样本数据出现的次数选择箱子的间隔,分箱后在每个箱子内数据数量尽量相等。
import numpy as np
import pandas as pd
from pandas import Series, DataFrame
score_list = np.linspace(0, 18, num=10)
print(score_list)
# [ 0. 2. 4. 6. 8. 10. 12. 14. 16. 18.]
score_cat = pd.cut(score_list, 2)
print(pd.value_counts(score_cat))
'''
(9.0, 18.0] 5
(-0.018, 9.0] 5
'''
score_cat = pd.cut(score_list, 3)
print(pd.value_counts(score_cat))
'''
(-0.018, 6.0] 4
(12.0, 18.0] 3
(6.0, 12.0] 3
'''
score_cat = pd.cut(score_list, 4)
print(pd.value_counts(score_cat))
'''
(13.5, 18.0] 3
(-0.018, 4.5] 3
(9.0, 13.5] 2
(4.5, 9.0] 2
'''
2.3.3 分箱后计算WOE和IV
对数据进行分箱操作后可以计算每个分组(箱子)中数据的WOE和IV。
如果对连续型特征进行分箱处理,需要对分箱后的每组(箱)数据进行WOE编码或IV编码处理,然后才可以用于训练模型。
案例 乳腺癌数据
import sklearn.datasets as ds
import numpy as np
import pandas as pd
from pandas import Series, DataFrame
bc = ds.load_breast_cancer()
feature = bc.data
target = bc.target
观察特征数据,判断特征数据是属于离散型还是连续型。
feature[:, 1].min(), feature[:, 1].max()
# (9.71, 39.28)
特征数据属于连续型,进行分箱处理。
# 这里只考虑第一个特征feature[:, 1]。
fea_bins = pd.cut(feature[:, 1], bins=5)
fea_bins.value_counts()
'''
(9.68, 15.624] 113
(15.624, 21.538] 299
(21.538, 27.452] 129
(27.452, 33.366] 25
(33.366, 39.28] 3
'''
对于连续型特征,需要对分箱后的特征列进行WOE编码。
查看标签数据
pd.Series(data=target).value_counts()
'''
1 357
0 212
'''
标签数据分别为0和1,表示对象是否患有乳腺癌。
将标签0规定为正例样本,将标签1规定为负例样本。
gi = pd.crosstab(fea_bins, target) # 交叉表
'''
col_0 0 1
row_0
(9.68, 15.624] 8 105
(15.624, 21.538] 101 198
(21.538, 27.452] 90 39
(27.452, 33.366] 11 14
(33.366, 39.28] 2 1
'''
交叉表解读:
每行表示一个分组,每一列表示标签,包括0和1。
col_0 0 1
row_0
(9.68, 15.624] 8 105
表示对于分组(9.68, 15.624],标签0(正例样本)的样本数量为8,标签1的样本数量为105。
gb = pd.Series(data=target).value_counts()
'''
1 357
0 212
'''
# gi表示分组后每组中各个特征样本数量;
# gb表示整体样本中各个特征样本数量。
gbi = (gi[0] / gi[1]) / (gb[0] / gb[1])
'''
(9.68, 15.624] 0.128302
(15.624, 21.538] 0.858991
(21.538, 27.452] 3.886067
(27.452, 33.366] 1.323113
(33.366, 39.28] 3.367925
'''
woe = np.log(gbi)
'''
(9.68, 15.624] -2.053369
(15.624, 21.538] -0.151997
(21.538, 27.452] 1.357398
(27.452, 33.366] 0.279987
(33.366, 39.28] 1.214297
'''
计算iv
iv = ((gi[0] / gi[1]) - (gb[0] / gb[1])) * woe
'''
(9.68, 15.624] 1.062921
(15.624, 21.538] 0.012728
(21.538, 27.452] 2.326382
(27.452, 33.366] 0.053723
(33.366, 39.28] 1.707498
'''
iv.sum() # 5.163252023882779
进行映射,将样本中的特征数据替换成所属组的iv值。
iv_dict = iv.to_dict()
ivs_bins = fea_bins.map(iv_dict)
3 样本类别分布不均衡处理
3.1 介绍
如果样本中属于不同标签类别的样本数量的差异非常大,那么就称这个样本类别分布不均衡。
样本类别分布不均衡的危害
样本类别分布不均衡将导致样本量少的标签分类所包含的特征过少,难以从中提取规律。即使得到了分类模型,也容易过度依赖于有限的样本,产生过拟合问题。当模型处理未知数据时,输出结果的准确程度会很差。
3.2 解决方法
通过过抽样和欠抽样解决样本类别分布不均衡问题,也可以称为上采样和下采样。
3.2.1 过抽样
过抽样(over-sampling),通过增加分类中少数类样本的数量来实现样本均衡,比较好的方法有SMOTE算法。
SMOTE算法思想
目标是合成新的少数类样本,
合成策略是对每个少数类中的样本数据a,从它的最近邻中随机选一个样本b,然后在a与b之间的连线上随机选取一点作为新合成的少数类样本。
准备数据
import pandas as pd
import numpy as np
x = np.random.randint(0, 100, size=(100, 3))
y = pd.Series(data=np.random.randint(0, 1, size=(95,)))
y = y.append(pd.Series(data=[1, 1, 1, 1, 1]), ignore_index=False).values
y = y.reshape((-1, 1))
all_data_np = np.concatenate((x, y), axis=1)
np.random.shuffle(all_data_np)
df = pd.DataFrame(all_data_np)
df.head()
'''
0 1 2 3
0 68 86 28 0
1 13 55 88 0
2 49 21 46 0
3 86 49 97 1
4 26 13 63 0
'''
df.shape # (100, 4)
df[3].value_counts()
'''
0 95
1 5
'''
X = df[[0, 1, 2]]
y = df[3]
SMOTE类的参数k_neighbors表示找出少数类的样本点周围最近的k个近邻样本。
from imblearn.over_sampling import SMOTE
X.shape # (100, 3)
y.value_counts()
'''
0 95
1 5
'''
s = SMOTE(k_neighbors=3)
feature, target = s.fit_sample(X, y)
feature.shape # (190, 3)
target.value_counts()
'''
1 95
0 95
'''
3.2.2 欠抽样
欠抽样(under-sampling),通过减少分类中多数类样本的数量来实现样本均衡。
from imblearn.under_sampling import RandomUnderSampler
X.shape # (100, 3)
y.value_counts()
'''
0 95
1 5
'''
r = RandomUnderSampler()
a, b = r.fit_sample(X, y)
a.shape # (10, 3)
b.value_counts()
'''
1 5
0 5
'''

