回溯Backtracking(17. 电话号码的字母组合、93. 复原 IP 地址、79. 单词搜索、257. 二叉树的所有路径、47. 全排列 II、77.组合、39、40、216、90、131)
目录
一、17. 电话号码的字母组合
1.1 题目描述
1.2 代码
1.2.1 回溯法
二、93. 复原 IP 地址
2.1 题目描述
2.2 代码
2.2.1 回溯
三、79. 单词搜索
3.1 题目描述
3.2 代码
四、257. 二叉树的所有路径
4.1 题目描述
4.2 代码
4.2.1 回溯
五、46. 全排列
5.1 题目描述
5.2 代码
5.2.1 回溯
六、47. 全排列 II
6.1 题目描述
6.2 代码
6.2.1 回溯
七、77. 组合
7.1 题目描述
7.2 代码
八、39. 组合总和
8.1 题目描述
8.2 代码
九、40. 组合总和 II
9.1 题目描述
9.2 代码
十、216. 组合总和 III
10.1 题目描述
10.2 代码
十一、78. 子集
11.1 题目描述
11.2 代码
十二、90. 子集 II
12.1 题目描述
12.2 代码
十三、131. 分割回文串
13.1 题目描述
13.2 代码
十四、37. 解数独
14.1 题目描述
14.2 代码
十五、51. N 皇后
15.1 题目描述
15.2 代码
一、17. 电话号码的字母组合
1.1 题目描述
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。(难度中等)
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
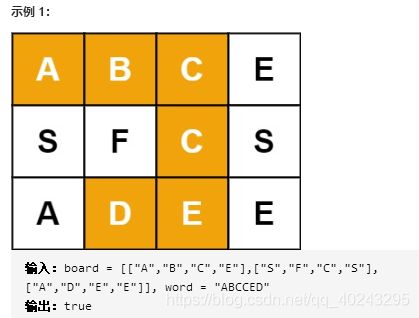
示例 1:输入:digits = "23"
输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]示例 2:输入:digits = ""
输出:[]示例 3:输入:digits = "2"
输出:["a","b","c"]
提示:0 <= digits.length <= 4
digits[i] 是范围 ['2', '9'] 的一个数字。
1.2 代码
1.2.1 回溯法
题解:力扣
/**
* 当对字符串进行修改的时候,需要使用 StringBuffer 和 StringBuilder 类。
*和 String 类不同的是,StringBuffer 和 StringBuilder 类的对象能够被多次的修改,并且不产生新的未使用对象。
* 它和 StringBuffer 之间的最大不同在于 StringBuilder 的方法不是线程安全的(不能同步访问)。
* 由于 StringBuilder 相较于 StringBuffer 有速度优势,所以多数情况下建议使用 StringBuilder 类。
**/
private static final String[] KEYS = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
public List letterCombinations(String digits) {
List combinations = new ArrayList<>();
if (digits == null || digits.length() == 0) {
return combinations;
}
doCombination(new StringBuilder(), combinations, digits);
return combinations;
}
//prefix前缀
private void doCombination(StringBuilder prefix, List combinations, final String digits) {
if (prefix.length() == digits.length()) {//说明此次组合成功,加入List
combinations.add(prefix.toString());
return;
}
int curDigits = digits.charAt(prefix.length()) - '0';//取出digits每位的值
String letters = KEYS[curDigits];//找到每一位对应字符的索引
for (char c : letters.toCharArray()) {//要将values转为数组,才可变量
prefix.append(c); // 添加
doCombination(prefix, combinations, digits);
prefix.deleteCharAt(prefix.length() - 1); // 删除,撤销你在这一步做的选择
}
} 补充:
当对字符串进行修改的时候,需要使用 StringBuffer 和 StringBuilder 类。
和 String 类不同的是,StringBuffer 和 StringBuilder 类的对象能够被多次的修改,并且不产生新的未使用对象。
它和 StringBuffer 之间的最大不同在于 StringBuilder 的方法不是线程安全的(线程安全:不能同步访问)。
由于 StringBuilder 相较于 StringBuffer 有速度优势,所以多数情况下建议使用 StringBuilder 类。
二、93. 复原 IP 地址
2.1 题目描述
给定一个只包含数字的字符串,用以表示一个 IP 地址,返回所有可能从 s 获得的 有效 IP 地址 。你可以按任何顺序返回答案。(难度中等)
有效 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 '.' 分隔。
例如:"0.1.2.201" 和 "192.168.1.1" 是 有效 IP 地址,但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是 无效 IP 地址。
提示:
0 <= s.length <= 3000s仅由数字组成
2.2 代码
2.2.1 回溯
使用回溯法判断,先加入若再剪枝
什么情况下剪枝呢?
ip地址由4段组成,k为现在确定的段数,若剩余的k-4段,每个都分配3为数字,s还有剩余的话,说明不能这样分ip,进行剪枝操作。
思路可参考:力扣
public static List restoreIpAddresses(String s) {
List addresses = new ArrayList<>();
StringBuilder tempAddress = new StringBuilder();
int len = s.length();
//若ip地址超过12或小于4不能凑成合法ip地址
if (len > 12 || len < 4) {
return addresses;
}
doRestore(0, tempAddress, addresses, s);
return addresses;
}
private static void doRestore(int k, StringBuilder tempAddress, List addresses, String s) {
//ip地址由4段组成,k为现在确定的段数,若剩余的4-k段,每个都分配3为数字,s还有剩余的话,说明不能这样分ip,进行剪枝操作
if ((s.length()-(4-k) * 3 >0 )){
return;
}
//k是有几段放好了,若四段都放好了,且无剩余ip地址,则成功,添加此分配方式
if (k == 4 && s.length() == 0) {
addresses.add(tempAddress.toString());
}
for (int i = 0; i < s.length() && i <= 2; i++) {//i代表小段中的数字
if (i != 0 && s.charAt(0) == '0') {
//i为0时,代表将截取1位,可以为0,若i!=0,说明将截取的是多位,则首字母不能为0
break;
}
String part = s.substring(0, i + 1);//截取s[0,i]
if (Integer.valueOf(part) <= 255) {
if (tempAddress.length() != 0) {
part = "." + part;
}
tempAddress.append(part);
doRestore(k + 1, tempAddress, addresses, s.substring(i + 1));
tempAddress.delete(tempAddress.length() - part.length(), tempAddress.length()); //删除区间[start,end)
}
} 三、79. 单词搜索
3.1 题目描述
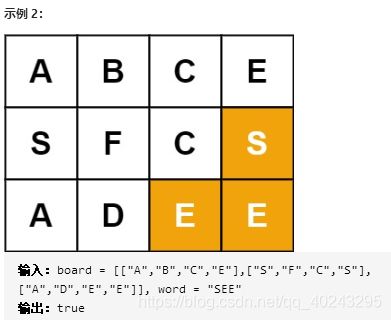
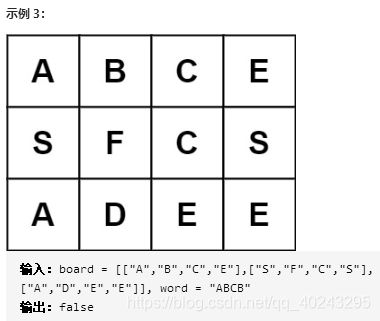
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。(难度中等)
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
3.2 代码
private final static int[][] direction = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
private int m;
private int n;
public boolean exist(char[][] board, String word) {
if (word == null || word.length() == 0) {
return true;
}
if (board == null || board.length == 0 || board[0].length == 0) {
return false;
}
m = board.length;
n = board[0].length;
boolean[][] hasVisited = new boolean[m][n];
for (int r = 0; r < m; r++) {
for (int c = 0; c < n; c++) {
if (backtracking(0, r, c, hasVisited, board, word)) {
return true;
}
}
}
return false;
}
private boolean backtracking(int curLen, int r, int c, boolean[][] visited, final char[][] board, final String word) {
if (curLen == word.length()) {
return true;
}
if (r < 0 || r >= m || c < 0 || c >= n
|| board[r][c] != word.charAt(curLen) || visited[r][c]) {
return false;
}
visited[r][c] = true;
for (int[] d : direction) {
if (backtracking(curLen + 1, r + d[0], c + d[1], visited, board, word)) {
return true;
}
}
visited[r][c] = false;
return false;
}四、257. 二叉树的所有路径
4.1 题目描述
给定一个二叉树,返回所有从根节点到叶子节点的路径。(难度简单)
说明: 叶子节点是指没有子节点的节点。
4.2 代码
4.2.1 回溯
遍历完左子树,构建出合格的路径,加入解集,遍历右子树之前,路径要撤销最末尾的选择,如果path用的是数组,就会弹出最后一项。
代码中用的字符串,pathStr保存了当前节点的路径,递归右子树时,传入它即可,它不包含在递归左子树所拼接的东西。
此处若为StringBuffer则不可以,因为它相当于一个全局变量,left修改后的,会传给right,不会消除
List res = new ArrayList<>();
String pathStr=null;
public List binaryTreePaths(TreeNode root) {
buildPath(root, "");
return res;
}
public void buildPath(TreeNode root, String pathStr) {
if (root == null) { // 遍历到null
return; // 结束当前递归分支
}
if (root.left == null && root.right == null) { // 遍历到叶子节点
pathStr += root.val; // 路径末尾了,不用加箭头
res.add(pathStr); // 加入解集
return;
}
pathStr = pathStr+ root.val + "->"; // 处理非叶子节点,要加箭头
buildPath(root.left, pathStr); // 基于当前的pathStr,递归左子树
buildPath(root.right, pathStr); // 基于当前的pathStr,递归右子树
}
} 五、46. 全排列
5.1 题目描述
给定一个 没有重复 数字的序列,返回其所有可能的全排列。(难度中等)
5.2 代码
5.2.1 回溯
private static List> permute(int[] nums) {
List> permutes = new ArrayList<>();
List perlist = new ArrayList<>();
if (nums == null || nums.length == 0)
return permutes;
boolean[] visited= new boolean[nums.length];
backtracking(nums,visited,perlist,permutes);
return permutes;
}
private static void backtracking(final int[] nums,boolean[] visited,List perlist,List> permutes){
if(perlist.size()== nums.length){//说明排列好一次,将其加入permutes
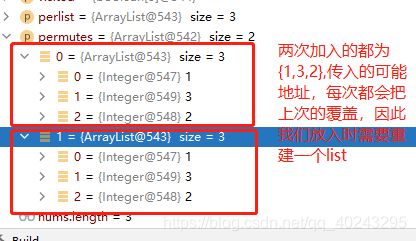
//permutes.add(perlist);//每次新加入会覆盖之前的值,循环两次变为了2个{1,3,2}
permutes.add(new ArrayList<>(perlist));//重新构建list
return;
}
for (int i = 0; i < nums.length; i++) {
if (visited[i]){
continue;
}
visited[i]=true;
perlist.add(nums[i]);
backtracking(nums, visited, perlist, permutes);
perlist.remove(perlist.size()-1);//回溯
visited[i]=false;
}
} 5.2.1 补充
1.ArrayList都是引用的地址
//permutes.add(perlist);//每次新加入会覆盖之前的值,循环两次变为了2个{1,3,2}
这说明list引用的都是地址。
修改代码:
// 重新构造一个 List,分步:
ArrayList integers = new ArrayList<>(perlist);
permutes.add(integers);
//合并,一步
permutes.add(new ArrayList<>(perlist)); 六、47. 全排列 II
6.1 题目描述
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。(难度中等)
6.2 代码
6.2.1 回溯
较46题代码只加入:
Arrays.sort(nums);
//backtracking中加入:
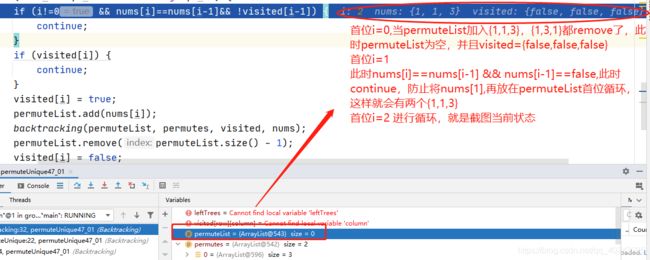
if (i!=0 && nums[i]==nums[i-1]&& !visited[i-1]) {
continue;
} public static List> permuteUnique(int[] nums) {
List> permutes = new ArrayList<>();
List perlist = new ArrayList<>();
if (nums == null || nums.length == 0)
return permutes;
Arrays.sort(nums);
boolean[] visited= new boolean[nums.length];
backtracking(nums,visited,perlist,permutes);
return permutes;
}
private static void backtracking(final int[] nums,boolean[] visited,List perlist,List> permutes){
if(perlist.size()== nums.length){//说明排列好一次,将其加入permutes
//permutes.add(perlist);//每次新加入会覆盖之前的值,循环两次变为了2个{1,3,2}
// ArrayList integers = new ArrayList<>(perlist);
// permutes.add(integers);// 重新构造一个 List
permutes.add(new ArrayList<>(perlist));
return;
}
for (int i = 0; i < nums.length; i++) {
if (visited[i]){
continue;
}
if (i!=0 && nums[i]==nums[i-1]&& !visited[i-1]) {
//为何!visited[i-1],博客下方有讲解
continue;
}
visited[i]=true;
perlist.add(nums[i]);
backtracking(nums, visited, perlist, permutes);
perlist.remove(perlist.size()-1);//回溯
visited[i]=false;
}
} 七、77. 组合
7.1 题目描述
7.2 代码
public List> combine(int n, int k) {
List> res=new ArrayList<>();
List cur=new ArrayList<>();
backing(n,k,res,cur,1);
return res;
}
//index为下次循环的起始标号
private void backing(int n, int k, List> res, List cur,int index) {
if (cur.size()==k){
res.add(new ArrayList<>(cur));
return;
}
for (int i = index; i <=n ; i++) {
cur.add(i);
backing(n,k,res,cur,i+1);
cur.remove(cur.size()-1);
}
} 但是我疑问的点是,为啥有时候回溯问题需要一个visited的标记已访问的数组,有时不需要?
都可以使用一个start来标记起始坐标,而不使用visited数组吗?
八、39. 组合总和
8.1 题目描述
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:所有数字(包括 target)都是正整数。解集不能包含重复的组合。
8.2 代码
public static List> combinationSum(int[] candidates, int target) {
List> combinationList = new ArrayList<>();
List list = new ArrayList<>();
backtracking(candidates,combinationList,list,0,target);
return combinationList;
}
public static void backtracking(int[] candidates, List> combinationList,
List list,int start,int target){
//target为现在所需的值
if (target==0) {
combinationList.add(new ArrayList<>(list));
return;
}
for (int i = start; i < candidates.length; i++) {
if (candidates[i]<=target){
list.add(candidates[i]);
backtracking(candidates,combinationList,list,i,target-candidates[i]);//每次循环还从当前开始
list.remove(list.size()-1);
}
}
} 九、40. 组合总和 II
9.1 题目描述
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的每个数字在每个组合中只能使用一次。
说明:所有数字(包括目标数)都是正整数。解集不能包含重复的组合。
9.2 代码
此题是八、47. 全排列 II和 六、39. 组合总和两题的结合
public static List> combinationSum2(int[] candidates, int target) {
Arrays.sort(candidates);
List> combinations = new ArrayList<>();
List tempCombination= new ArrayList<>();
boolean visited[] =new boolean[candidates.length];
backtracking(tempCombination, combinations, 0, target, candidates,visited);
return combinations;
}
public static void backtracking(List tempCombination,
List> combinations,
int start, int target,
final int[] candidates,boolean visited[]){
if (target==0){
combinations.add(new ArrayList<>(tempCombination));
return;
}
for (int i = start; i < candidates.length; i++) {
if (visited[i]){
continue;
}
if (i!=0 &&candidates[i]==candidates[i-1] && visited[i-1]==false){
continue;
}
if (candidates[i]<=target){
visited[i]=true;
tempCombination.add(candidates[i] );
backtracking(tempCombination, combinations, i+1, target-candidates[i], candidates,visited);
visited[i]=false;
tempCombination.remove(tempCombination.size()-1);
}
}
} 十、216. 组合总和 III
10.1 题目描述
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。
说明:所有数字都是正整数。解集不能包含重复的组合。
10.2 代码
public static List> combinationSum3(int k, int n) {
List> combinations = new ArrayList<>();
List tempCombination= new ArrayList<>();
int target=n;//n不变,target是剩余值
backtracking(tempCombination, combinations, 1, k, target,n);
return combinations;
}
public static void backtracking(List tempCombination,
List> combinations,
int start, int k, int target,int n){
if (target==0 && k==0){
combinations.add(new ArrayList<>(tempCombination));
return;
}
if (target==0 || k==0){
return;
}
for (int i = start; i < n && i<=9; i++) {
if (i<=target && k>0){
tempCombination.add(i);
//因为下一次从回溯从i+1开始,因此不需要visited数组标记
backtracking(tempCombination, combinations, i+1, k-1, target-i,n);
tempCombination.remove(tempCombination.size()-1);
}
}
} 十一、78. 子集
11.1 题目描述
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
11.2 代码
public static List> subsets(int[] nums) {
List> subsets = new ArrayList<>();
List tempSubset = new ArrayList<>();
for (int i = 0; i <= nums.length; i++) {//i是长度
backtracking(tempSubset, subsets, nums ,0, i);
}
return subsets;
}
public static void backtracking(List tempSubset,
List> subsets,int nums[],
int start, int size){//start 起始位置
if (tempSubset.size()==size){
subsets.add(new ArrayList<>(tempSubset));
return;
}
for (int j = start; j < nums.length; j++) {//j是遍历的地址
tempSubset.add(nums[j]);
backtracking(tempSubset,subsets,nums,j+1,size);
tempSubset.remove(tempSubset.size()-1);
}
} 十二、90. 子集 II
12.1 题目描述
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。
12.2 代码
public static List> subsetsWithDup(int[] nums) {
Arrays.sort(nums);
List> subsets = new ArrayList<>();
List tempSubset = new ArrayList<>();
boolean visited[] = new boolean[nums.length];
for (int len = 0; len <= nums.length; len++) {
backtracking(subsets, tempSubset, nums, 0, len,visited);
}
return subsets;
}
public static void backtracking(List> subsets,List tempSubset,
int[] nums,int start,int len,boolean[] visited){
if (tempSubset.size()==len) {
subsets.add(new ArrayList<>(tempSubset));
return;
}
for(int i = start; i < nums.length; i++) {
if (i!=0 && nums[i]==nums[i-1]&& visited[i-1]==false){
continue;
}
tempSubset.add(nums[i]);
visited[i]=true;
backtracking(subsets, tempSubset, nums, i+1, len,visited);
visited[i]=false;
tempSubset.remove(tempSubset.size()-1);
}
} 十三、131. 分割回文串
13.1 题目描述
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
回文串 是正着读和反着读都一样的字符串。
13.2 代码
s.substring(i+1):截取字符串,从索引i+1开始到结束 public static List> partition(String s) {
List> partitions =new ArrayList<>();
List tempartition =new ArrayList<>();
backtracking(partitions,tempartition,s);
return partitions;
}
public static void backtracking(List> partitions,List tempartition,String s){
if (s.length() == 0) {
partitions.add(new ArrayList<>(tempartition));
return;
}
for (int i = 0; i < s.length(); i++) {
//先判断前i是不是回文,若是再判断i之后的,i从0取到s.length()
if (isPalindrome(s,0,i))
tempartition.add(s.substring(0,i+1));
backtracking(partitions,tempartition,s.substring(i+1));//s.substring(i+1)索引从i+1开始到结束
tempartition.remove(tempartition.size()-1);
}
}
}
public static boolean isPalindrome(String s,int start,int end){
while (start
十四、37. 解数独
14.1 题目描述
编写一个程序,通过填充空格来解决数独问题。
数独的解法需 遵循如下规则:
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 '.' 表示。
14.2 代码
题解思路链接
思路:
最容易想到的方法是用一个数组记录每个数字是否出现。由于我们可以填写的数字范围为[1,9],而数组的下标从 0开始,因此在存储时,我们使用一个长度为 9 的布尔类型的数组,其中 i 个元素的值为True,当且仅当数字i+1 出现过。例如我们用line[2][3]=True 表示数字 4 在第 2 行已经出现过,那么当我们在遍历到第 2 行的空白格时,就不能填入数字 4。
并且设置一个vaild变量,若vaild==true时,代表全部填入成功,结束程序,不再遍历。
算法:
我们首先对整个数独数组进行遍历,当我们遍历到第 i行第 j 列的位置:
- 如果该位置是一个空白格,那么我们将其加入一个用来存储空白格位置的列表spaces中,方便后续的递归操作;
- 如果该位置是一个数字 digit,那么我们需要将line[i][digit−1],column[j][digit−1] 以及block[⌊i/3⌋][⌊j/3⌋][digit−1] 均置True。
当我们结束了遍历过程之后,就可以开始递归枚举。当递归到第 i 行第 j列的位置时,我们枚举填入的数字digit。根据题目的要求,数字digit 不能和当前行、列、九宫格中已经填入的数字相同,因此line[i][digit−1],column[j][digit−1] 以及block[⌊i/3⌋][⌊j/3⌋][digit−1] 必须均为False。
当我们填入了数字 digit 之后,我们要将上述的三个值都置为True,并且继续对下一个空白格位置进行递归。在回溯到当前递归层时,我们还要将上述的三个值重新置为 False。
private boolean[][] line=new boolean[9][9];
private boolean[][] column=new boolean[9][9];
private boolean[][][] block=new boolean[3][3][9];
private List spaces = new ArrayList<>();
boolean vaild=false;
public void solveSudoku(char[][] board) {
//遍历
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
if (board[i][j] == '.') {
spaces.add(new int[]{i, j});
} else {
int digit = board[i][j] - '0' - 1;
line[i][digit] = column[j][digit] = block[i / 3][j / 3][digit] = true;
}
}
}
backtracking(board,0);
}
private void backtracking(char[][] board, int pos) {
if (pos==spaces.size()){
vaild=true;
return;
}
int[] space = spaces.get(pos);
int i=space[0],j=space[1];
for (int digit = 0; digit <9 && !vaild ; digit++) {
if (!line[i][digit] && !column[j][digit]&& !block[i/3][j/3][digit]){
line[i][digit] = column[j][digit]=block[i/3][j/3][digit]=true;
board[i][j]= (char) (digit+'0'+1);
backtracking(board,pos+1);
line[i][digit]=column[j][digit]=block[i/3][j/3][digit]=false;
}
}
}
十五、51. N 皇后
15.1 题目描述
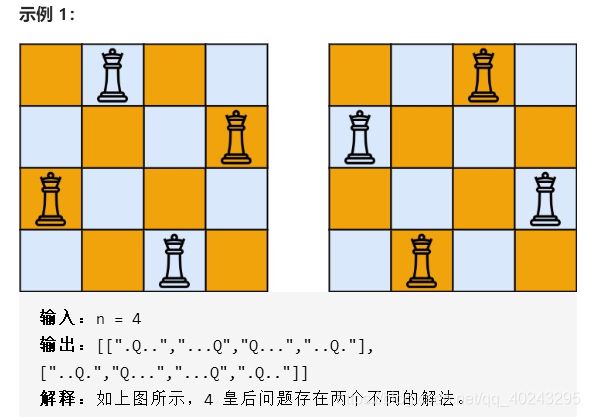
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
15.2 代码
题解链接
思路:
为了判断一个位置所在的列和两条斜线上是否已经有皇后,使用三个集合columns、diagonals 1、diagonals 2分别记录每一列以及两个方向的每条斜线上是否有皇后。列的表示法很直观,一共有 N 列,每一列的下标范围从 0 到 N-1,使用列的下标即可明确表示每一列。
如何表示两个方向的斜线呢?对于每个方向的斜线,需要找到斜线上的每个位置的行下标与列下标之间的关系。
从左上到右下方向斜线,行下标-列下标=固定值
从右上到左下方向斜线, 行下标+列下标=固定值
public List> solveNQueens(int n) {
List> solutions = new ArrayList>();
int[] queens = new int[n];//queens[i]是行?
Arrays.fill(queens, -1);
Set columns = new HashSet();//判断列位置
Set diagonals1 = new HashSet();
Set diagonals2 = new HashSet();
backtrack(solutions, queens, n, 0, columns, diagonals1, diagonals2);
return solutions;
}
public void backtrack(List> solutions, int[] queens, int n, int row, Set columns, Set diagonals1, Set diagonals2) {
if (row == n) {
List board = generateBoard(queens, n);
solutions.add(board);
} else {
for (int i = 0; i < n; i++) {
if (columns.contains(i)) {
continue;
}
int diagonal1 = row - i;//从左上到右下方向,行下标-列下标=固定值
if (diagonals1.contains(diagonal1)) {
continue;
}
int diagonal2 = row + i;//从右上到左下方向,行下标+列下标=固定值
if (diagonals2.contains(diagonal2)) {
continue;
}
queens[row] = i;
columns.add(i);
diagonals1.add(diagonal1);
diagonals2.add(diagonal2);
backtrack(solutions, queens, n, row + 1, columns, diagonals1, diagonals2);
queens[row] = -1;
columns.remove(i);
diagonals1.remove(diagonal1);
diagonals2.remove(diagonal2);
}
}
}
public List generateBoard(int[] queens, int n) {
List board = new ArrayList();
for (int i = 0; i < n; i++) {
char[] row = new char[n];
Arrays.fill(row, '.');
row[queens[i]] = 'Q';
board.add(new String(row));
}
return board;
}