计算机算法分析与设计（21）---回溯法(图着色问题)

---

一、背景知识

 1. 为地图或其他由不同区域组成的图形着色时，相邻国家/地区不能使用相同的颜色。 我们可能还想使用尽可能少的不同颜色进行填涂。一些简单的“地图”（例如棋盘）仅需要两种颜色（黑白），但是大多数复杂的地图需要更多的颜色。

 2. （1）每张地图包含四个相互连接的国家时，它们至少需要四种颜色。1852年，植物学专业的学生弗朗西斯·古思里（Francis Guthrie）于1852年首次提出“四色问题”。他观察到四种颜色似乎足以满足他尝试的任何地图填色问题，但他无法找到适用于所有地图的证明。这个问题被称为四色问题。
 （2）长期以来，数学家无法证明四种颜色就够了，或者无法找到需要四种以上颜色的地图。直到1976年德国数学家沃尔夫冈·哈肯（Wolfgang Haken，生于1928年）和肯尼斯·阿佩尔（Kenneth Appel，1932年-2013年）使用计算机证明了四色定理，他们将无数种可能的地图缩减为1936种特殊情况，每种情况都由一台计算机进行了总计超过1000个小时的检查。

 3. 四色定理是第一个使用计算机证明的著名数学定理，此后变得越来越普遍，争议也越来越小 更快的计算机和更高效的算法意味着今天您可以在几个小时内在笔记本电脑上证明四种颜色定理。

二、问题转换与描述

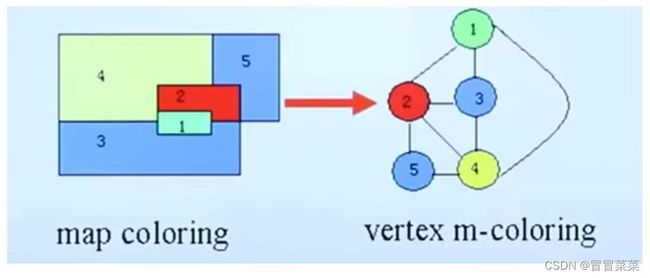
 1. 一个地图用一个平面图 $G$ 表示。将地图的每个区域用图 $G$ 的一个结点表示，若两个区域相邻，则相应的两个结点用一条边连接起来。

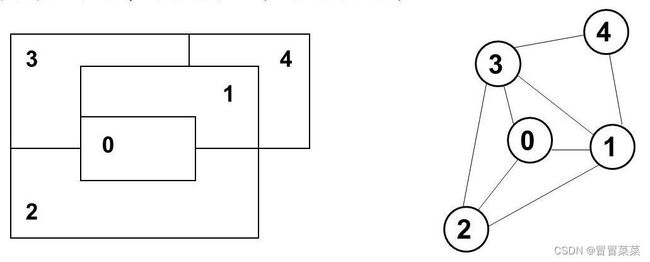
 2. 点 $m$–着色问题：给定一个无向图 $G=(V,E)$，需要对图 $G$ 中的每个顶点用 $m$ 种颜色中的一种着色，记为 $1,2,......m$，使得相邻的顶点不同色。

三、算法讲解

3.1 思路分析

 1. 采用 $n$ 元组 $(x_0,x_1,...x_{n-1})$ 表示图 $G$ 的 $m$–着色问题的解，并采用邻接矩阵表示无向图 $G=(V,E)$。

• $a[i][j]=1，(i,j)\in E$
• $a[i][j]=0，其他$

 2. 显示约束：$n$ 元组 $(x_0,x_1,...x_{n-1}),x_i\in [1,\mathrm{2...},m],1\le i\le n$ 表示节点的 $i$ 的颜色。$x_i=0$ 表示没有可用的颜色。因此解空间的大小为 $m^n$。
 隐式约束：如果边 $(i,j)\in E$，则 $x_i\ne x_j$，即此时 $a[i][j]=1$。

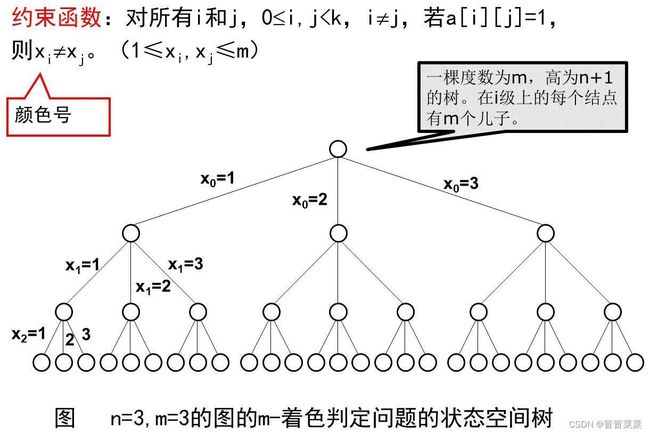
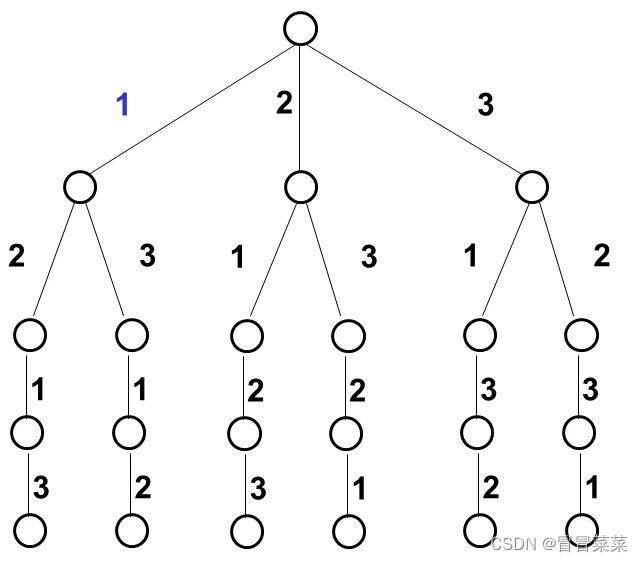
3.2 状态空间生成树

3.3 代码编写

时间复杂性 $O(n{m}^n)$
使用深度优先搜索（DFS）从解空间树的根节点开始搜索，并在每个分支结点处调用 $ok()$ 函数来剪枝。如果在整棵解空间树中找到了一组可行解，那么算法就停止搜索并输出结果。如果找不到任何一个可行解，则算法输出无解信息。
具体实现过程：
首先，需要定义一个二维数组 $G[][]$，用于存储图中的边。其中，$G[u][v]==1$ 表示节点 $u$ 和节点 $v$ 之间有边相连，反之为 $0$。同时，还需要定义一个一维数组 $color[]$，用于存储每个节点的颜色。
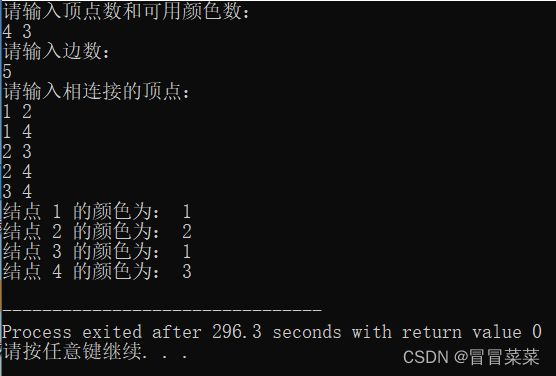
最初将所有边权赋值为 $0$，即不存在边。然后，读入所有边，将对应的边权赋值为 $1$。读入颜色数 $m$，并从节点 $1$ 开始做深度优先搜索，依次尝试给每个节点涂上不同的颜色。在每个分支结点处，使用 $ok()$ 函数来判断是否符合要求。如果染色成功，则继续对下一个节点做深度优先搜索。如果找到了一组可行解，则输出结果。

#include 
#include 
using namespace std;

const int maxn = 1005;
int G[maxn][maxn], color[maxn];//用于存储图中的边--用于存储每个节点的颜色 
int n, m;                      //n表示图中节点的数量，m表示可供选择的颜色数目。
 
bool ok(int u, int c){
    for (int i = 1; i <= n; i++)
	{
        if (G[u][i] == 1 && color[i] == c)
            return false;
    }
    return true;
}
 
bool dfs(int u){
    if (u > n)
        return true;
    for (int i = 1; i <= m; i++)
	{
        if (ok(u, i))
		{
            color[u] = i;
            if (dfs(u + 1))
                return true;
            color[u] = 0;
        }
    }
    return false;
}
 
int main(){
    memset(G, 0, sizeof(G));        //初始化邻接矩阵为0
    memset(color, 0, sizeof(color));//初始化颜色为0
    int e;                          //e表示图中边的数量
    cout << "请输入顶点数和可用颜色数：" << endl;
    cin >> n >> m;
    cout << "请输入边数：" << endl;
    cin >> e;
	cout << "请输入相连接的顶点：" << endl; //顶点从1开始
    for (int i = 0; i < e; i++)
	{
        int u, v;
        cin >> u >> v;
        G[u][v] = G[v][u] = 1;
    }
 
    if (dfs(1))
	{
        for (int i = 1; i <= n; i++) //顶点从1开始
		{
            cout << "结点 " << i << " 的颜色为： " << color[i] << endl;
        }
    }
    else
	{
        cout << "No solution" << endl;
    }
    return 0;
}