LeetCode - 刷题记录

LeetCode 203 移除链表元素

// 递归解法
class Solution {
    public ListNode removeElements(ListNode head, int val) {
        if(head == null) return null;
        ListNode tail = removeElements(head.next, val);
        if(head.val == val) return tail;
        head.next = tail;
        return head;
    }
}

// 迭代解法
class Solution {
    public ListNode removeElements(ListNode head, int val) {
        ListNode hh = new ListNode(0, head), pre = hh;
        while(pre.next != null) {
            if(pre.next.val == val) pre.next = pre.next.next;
            else pre = pre.next; 
        }
        return hh.next;
    }
}

LeetCode 200. 岛屿数量

图的遍历（DFS，BFS均可），或并查集进行集合合并

// dfs
class Solution {
    int[] dx = {1, -1, 0, 0};
    int[] dy = {0, 0, 1, -1};
    public int numIslands(char[][] grid) {
        int n = grid.length, m = grid[0].length;
        int ans = 0;
        for(int i = 0; i < n; i++) {
            for(int j = 0; j < m; j++) {
                if(grid[i][j] == '1') {
                    ans++;
                    dfs(grid, i, j);
                }
            }
        }
        return ans;
    }

    private void dfs(char[][] grid, int i, int j) {
        int n = grid.length, m = grid[0].length;
        if(i < 0 || i >= n || j < 0 || j >= m || grid[i][j] == '0') return;
        grid[i][j] = '0';
        for(int k = 0; k < 4; k++) dfs(grid, i + dx[k], j + dy[k]);
    }
}

LeetCode 92. 反转链表II

class Solution {
    public ListNode reverseBetween(ListNode head, int left, int right) {
        ListNode hh = new ListNode(0, head), pre = hh;
        for(int i = 1; i < left; i++) pre = pre.next;
        ListNode start = pre.next, cur = start , preCur = null;
        for(int i = left; i <= right; i++) {
            ListNode nextCur = cur.next;
            cur.next = preCur;
            preCur = cur;
            cur = nextCur;
        }
        start.next = cur;
        pre.next = preCur;
        return hh.next;
    }
}

LeetCode 54. 螺旋链表

解法一：朴素模拟

// 朴素模拟
class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> ans = new ArrayList<>();
        int n = matrix.length, m = matrix[0].length;
        int[][] direction = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
        int directionIndex = 0;
        boolean[][] st = new boolean[n][m];
        int x = 0, y = 0;
        for(int i = 0; i < n * m; i++) {
            ans.add(matrix[x][y]);
            st[x][y] = true;
            int nx = x + direction[directionIndex][0];
            int ny = y + direction[directionIndex][1];
            // 是否要换方向
            if(nx < 0 || nx >= n || ny < 0 || ny >= m || st[nx][ny]) directionIndex = (directionIndex + 1) % 4;
            x += direction[directionIndex][0];
            y += direction[directionIndex][1];
        }
        return ans;
    }
}

解法二：按层次模拟（设置上下左右边界，每次顺时针遍历最外一圈）

// 按层模拟
class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> ans = new ArrayList<>();
        int n = matrix.length, m = matrix[0].length;
        int top = 0, left = 0, right = m - 1, bottom = n - 1;
        while(bottom >= top && right >= left) {
            for(int i = left; i <= right; i++) ans.add(matrix[top][i]);
            top++;
            if(top > bottom) break; //最后一次遍历, 两个边界相交了, 要提前break
            for(int i = top; i <= bottom; i++) ans.add(matrix[i][right]);
            right--;
            if(right < left) break;
            for(int i = right; i >= left; i--) ans.add(matrix[bottom][i]);
            bottom--;
            if(bottom < top) break;
            for(int i = bottom; i >= top; i--) ans.add(matrix[i][left]);
            left++;
            if(left > right) break;
        }
        return ans;
    }
}

LeetCode 42. 接雨水

思路：

• 按行求（依次求高度1，高度2，高度3，…，那一行中的雨水）
• 按列求（一次求每一列，可能接到的雨水）

按行求会超时，现只考虑按列求，基本思路：每一列，先求出其左边高度最高的列，以及右边高度最高的列，这两个高度取一个最小值，若这个最小值大于当前列的高度，则当前列的位置能够接到雨水

• 暴力：$O(n^2)$
• 动态规划：$O(n)$，实际运算次数是3n，预处理出leftMost，rightMost数组
• 双指针（动规的优化）：$O(n)$，实际运算次数是n
• 单调栈：$O(n)$

暴力

从左到右依次遍历每个位置，遍历当前位置i时，向左求解出i左侧的最高高度leftMost，向右求出i右侧的最高高度rightMost。取leftMost和rightMost中的较小者min，当min大于当前位置的高度height[i] 时，则在位置i能接到雨水，接到雨水的量为 min - height[i]。由于第一个位置，和最后一个位置，都无法接到雨水，因为其左侧和右侧分别为空，所以遍历时我们可以从第二个位置，遍历到倒数第二个位置即可。

时间复杂度：外层循环是n次，每次循环时，向左遍历，向右遍历，总共遍历n-1个位置（除去当前位置），能够求出leftMost和rightMost，所以总的运算次数就是n * (n - 1)，复杂度为 $O(n^2)$

// 暴力
class Solution {
    public int trap(int[] height) {
        int n = height.length;
        int ans = 0;
        for (int i = 1; i < n - 1; i++) {
            int leftMost = 0, rightMost = 0;
            for (int j = i - 1; j >= 0; j--) leftMost = Math.max(leftMost, height[j]);
            for (int j = i + 1; j < n; j++) rightMost = Math.max(rightMost, height[j]);
            int h = Math.min(leftMost, rightMost);
            if (h > height[i]) ans += h - height[i];
        }
        return ans;
    }
}

动态规划

在暴力做法中，对每个位置求解leftMost和rightMost时，做了很多重复的运算。比如在位置i时，求解leftMost，我们已经遍历了i - 1到0 这些位置；在位置i + 1 时，会遍历 i 到0的位置，其中重复遍历了i - 1到0。其实我们可以复用先前的计算结果。
我们可以预处理出每个位置的leftMost和rightMost值。
设 leftMost[i] 表示第i个位置左侧的最高柱子的高度，则状态转移方程为：
leftMost[i] = max(leftMost[i - 1], height[i - 1])
即，第i个位置左侧的最高柱子高度，要么等于第i - 1个位置左侧的最高柱子高度，要么等于第i - 1个位置的柱子高度。
同理，有：
rightMost[i] = max(rightMost[i + 1], height[i + 1])
则我们从左往右遍历一次，能预处理出所有的leftMost[i]，从右往左遍历一次，能预处理出所有的rightMost[i]，最后再遍历一次，进行计算。总共的运算次数是 3n，所以时间复杂度为 $O(n)$

// 动规
class Solution {
    public int trap(int[] height) {
        int n = height.length;
        int[] leftMost = new int[n], rightMost = new int[n];
        for (int i = 1; i < n; i++) leftMost[i] = Math.max(height[i - 1], leftMost[i - 1]);
        for (int i = n - 2; i >= 0; i--) rightMost[i] = Math.max(height[i + 1], rightMost[i + 1]);
        int ans = 0;
        for (int i = 1; i <= n - 2; i++) {
            int h = Math.min(leftMost[i], rightMost[i]);
            if (h > height[i]) ans += h - height[i];
        }
        return ans;
    }
}

双指针

我们在从左往右进行计算时，其实可以同步处理出当前位置的leftMost，所以对leftMost数组的预处理，可以省掉，如下

class Solution {
    public int trap(int[] height) {
        int n = height.length;
        int[] rightMost = new int[n];
        int leftMost = 0;
        for (int i = n - 2; i >= 0; i--) rightMost[i] = Math.max(height[i + 1], rightMost[i + 1]);
        int ans = 0;
        for (int i = 1; i <= n - 2; i++) {
            leftMost = Math.max(leftMost, height[i - 1]);
            int h = Math.min(leftMost, rightMost[i]);
            if (h > height[i]) ans += h - height[i];
        }
        return ans;
    }
} 

但是我们的rightMost需要从右往左进行处理。

我们考虑用双指针来从左右两侧往中间遍历处理。
我们设如下变量：
leftMost： 记录左侧最大值，是从左到右找到的
rightMost ：记录右侧最大值，是从右往左找到的
i ：从左往右处理时的当前下标
j：从右往左处理时的当前下标

在处理i这个位置时，由于i是从左往右遍历的，i的左侧最大值是确定的，有iLeftMost = leftMost，而此时的rightMost并不是准确的，因为位置i到j中间的情况是未知的。若中间有柱子的高度大于此时的rightMost，那对位置i来说，iRightMost必然大于 rightMost。即，对于位置i来说，其左侧最大值iLeftMost就是leftMost，而其右侧最大值iRightMost >= rightMost。而如果此时leftMost < rightMost，由于rightMost <= iRightMost，那就能得出iLeftMost < iRightMost，则位置i能接到的雨水量，由iLeftMost决定，即由leftMost决定，此时可以对位置i能接到的雨水进行计算，并右移i。
同理，在处理j这个位置时，由于j是从右往左遍历的，jRightMost就等于rightMost，而jLeftMost >= leftMost。如果此时rightMost < leftMost，则有jRightMost = rightMost < leftMost <= jLeftMost，即jRightMost < jLeftMost。则此时位置j能接到的雨水，由jRightMost决定，即由rightMost决定，此时可以对位置j能接到的雨水进行计算，并左移j。
当i和j相遇并跨过对方时，结束循环即可。

class Solution {
    public int trap(int[] height) {
        int n = height.length;
        int leftMost = height[0], rightMost = height[n - 1];
        int i = 1, j = n - 2;
        int ans = 0;
        while (i <= j) {
            if (leftMost <= rightMost) {
                if (leftMost > height[i]) ans += leftMost - height[i];
                leftMost = Math.max(leftMost, height[i++]);
            } else {
                if (rightMost > height[j]) ans += rightMost - height[j];
                rightMost = Math.max(rightMost, height[j--]);
            }
        }
        return ans;
    }
}

单调栈

说到栈，我们肯定会想到括号匹配了。我们仔细观察蓝色的部分，可以和括号匹配类比下。每次匹配出一对括号（找到对应的一堵墙），就计算这两堵墙中的水。

我们用栈保存每堵墙。

当遍历墙的高度的时候，如果当前高度小于栈顶的墙高度，说明这里会有积水，我们将墙的高度的下标入栈。

如果当前高度大于栈顶的墙的高度，说明之前的积水到这里停下，我们可以计算下有多少积水了。计算完，就把当前的墙继续入栈，作为新的积水的墙。

class Solution {
    public int trap(int[] height) {
        Deque<Integer> stack = new LinkedList<>();
        int ans = 0;
        for (int i = 0; i < height.length; i++) {
            while (!stack.isEmpty() && height[stack.peek()] < height[i]) {
                int j = stack.pop();
                if (stack.isEmpty()) break;
                int h = Math.min(height[stack.peek()], height[i]);
                int dis = i - stack.peek() - 1;
                if (h > height[j]) ans += (h - height[j]) * dis;
            }
            stack.push(i);
        }
        return ans;
    }
}

LeetCode 93. 复原ip地址

简单dfs，注意要考虑边界条件，处理前缀0

class Solution {
    public List<String> restoreIpAddresses(String s) {
        int[] path = new int[4];
        List<String> ans = new ArrayList<>();
        dfs(0, 0, s, path, ans);
        return ans;
    }

    private void dfs(int x, int index, String s, int[] path, List<String> ans) {
        if (x == 4) {
            if (index != s.length()) return;
            StringBuilder sb = new StringBuilder();
            for (int i : path) sb.append(i).append('.');
            sb.deleteCharAt(sb.length() - 1);
            ans.add(sb.toString());
            return;
        }
        int sum = 0;
        for (int i = index; i < s.length(); i++) {
            sum = sum * 10 + s.charAt(i) - '0';
            if (sum > 255) return;
            path[x] = sum;
            dfs(x + 1, i + 1, s, path, ans);
            if (sum == 0) return; // 处理前缀0, 跳过后续
        }
    }
}

LeetCode 199. 二叉树的右视图

• 层序遍历BFS，插入每一层的最后一个节点
• 深搜DFS，额外维护节点的深度

// BFS
class Solution {
    public List<Integer> rightSideView(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        if (root == null) return ans;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            int size = queue.size();
            TreeNode x = null;
            while (size-- > 0) {
                x = queue.poll();
                if (x.left != null) queue.offer(x.left);
                if (x.right != null) queue.offer(x.right);
            }
            ans.add(x.val);
        }
        return ans;
    }
}

// DFS
class Solution {
    public List<Integer> rightSideView(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        int depth = 0;
        dfs(root, ans, depth);
        return ans;
    }

    private void dfs(TreeNode x, List<Integer> ans, int depth) {
        if (x == null) return;
        if (depth == ans.size()) ans.add(x.val);
        dfs(x.right, ans, ++depth);
        dfs(x.left, ans, depth);
    }
}

LeetCode 124. 二叉树中的最大路径和

解法一：自己想的，dfs + 动规

注意题目的描述，一条路径是从任意一个节点走到另一个节点，途中经过的节点的序列，且同一节点只能出现一次，即已经走过的路径无法往回走（一笔画，一笔就能把整条路径勾勒出来）。

则在这条路径上，若一个节点x在路径上，且x的左右儿子也都在路径上，则这样的节点x，最多只能有1个。其余的节点，其左右儿子，最多只能有1个在路径上。否则路径就会有多处分叉，无法通过一笔就画出路径。

初始的思路是这样的：联想到这道题：没有上司的舞会

通过动态规划的思想，设有如下的状态表示

f(x, 1) 表示，从节点x往下，所有经过x的路径中，最大的路径和

f(x, 0) 表示，从节点x往下，所有不经过x的路径中，最大的路径和

则最终的答案就是 max{ f(root, 1), f(root, 0) }

接下来考虑状态转移，先考虑f(x, 1)，f(x, 1) 一定要包含节点x，那么其向左右两边往下走。若其走到左儿子，则路径一定要包含左儿子，否则无法往下走；若其走到右儿子，则路径一定要包含右儿子。

从x的左儿子往下走，且经过左儿子的路径中，最大的路径和就是 f(x.leftSon, 1)

从x的右儿子往下走，且经过右儿子的路径中，最大的路径和就是 f(x.rightSon, 1)

对于 f(x, 1)，路径一定包含节点x本身，可以选择是否纳入x左侧的路径，和x右侧的路径。

若x左侧的路径 f(x.leftSon, 1) 为负数，纳入会降低总的路径和，则不纳入；对于x右侧的路径同理

所以，f(x, 1)就在以下几个情况下取最大值即

• 左右侧的路径都不纳入
• 只纳入左侧路径
• 只纳入右侧路径
• 左右侧路径都纳入

另外，由于分叉只能发送在x节点本身，即只有x节点可以同时往左右扩展。对于x一下的节点，则只能单向扩展（只能扩展左侧，或只能扩展右侧），所以我们还要加一个额外的参数，来控制允许扩展的分叉。

f(x, 1, 2) 表示，从节点x往下，且经过x节点，且允许x节点往两侧扩展，的最大路径和

f(x, 1, 1) 表示，从节点x往下，且经过x节点，且只允许x节点往单侧扩展，的最大路径和

则状态转移方程便是

设 f(x.leftSon, 1, 1)为 left，设f(x.rightSon, 1, 1) 为right

则

f(x, 1, 2) = max { x.val, x.val + left, x.val + right, x.val + left + right }

对于f(x, 0, 2)，其值为以下几个情况取最大值

• f(x.leftSon, 1, 2)
• f(x.leftSon, 0, 2)
• f(x.rightSon, 1, 2)
• f(x.rightSon, 0, 2)

根据这个思路， 写出代码如下（需要注意控制对于空节点的处理，需要跳过空节点）

// 202ms
// 43MB
class Solution {
    int ans;
    public int maxPathSum(TreeNode root) {
        ans = dfs(root, 1, 1); // 经过根节点的路径
        // 只有当其左右儿子至少存在其一时, 才计算不包含根节点的路径
        if (root.left != null || root.right != null) ans = Math.max(ans, dfs(root, 0, 1));
        return ans;
    }

    // u: 是否经过当前节点, 1 是, 0 否
    // dual 是否允许往两边扩展, 1 是, 0 否
    // 手动控制x不会为null
    private int dfs(TreeNode x, int u, int dual) {
        if (u == 1) {
            // 需要经过当前节点
            if (x.left == null && x.right == null) return x.val;
            int ans = x.val, temp = x.val;
            boolean hasL = false, hasR = false;
            if (x.left != null) {
                // 左侧单边
                int l = dfs(x.left, 1, 0);
                ans = Math.max(ans, x.val + l);
                hasL = true;
                temp += l;
            }
            if (x.right != null) {
                // 右侧单边
                int r = dfs(x.right, 1, 0);
                ans = Math.max(ans, x.val + r);
                hasR = true;
                temp += r;
            }
            // 若当前节点允许走双边
            if(dual == 1 && hasL && hasR) ans = Math.max(ans, temp);
            return ans;
        } else {
            // 不走当前节点
            // 取左右节点的最大值
            Integer ans = null;
            if(x.left != null) {
                int l = dfs(x.left, 1, 1); // 可双边扩展, 走左侧节点
                if (x.left.left != null || x.left.right != null) l = Math.max(l, dfs(x.left, 0, 1)); // 可以不走左侧节点
                ans = l;
            }
            if (x.right != null) {
                int r = dfs(x.right, 1, 1); // 可双边扩展, 走右侧节点
                if (x.right.left != null || x.right.right != null) r = Math.max(r, dfs(x.right, 0, 1));
                ans = ans == null ? r : Math.max(ans, r);
            }
            return ans;
        }
    }
}

解法二：dfs + 记录答案

每条路径，都有一个顶点，顶点是这条路径最高的点（最靠近根节点的点）。在顶点处，至多可以选择往两边扩展。

我们只要遍历这棵树，对每个点作为顶点，求一下该点作为顶点的最大路径即可。

class Solution {

    int ret = Integer.MIN_VALUE;

    public int maxPathSum(TreeNode root) {
        dfs(root);
        return ret;
    }

    private int dfs(TreeNode x) {
        if (x == null) return 0;
        int l = Math.max(0, dfs(x.left));
        int r = Math.max(0, dfs(x.right));
        ret = Math.max(ret, x.val + l + r);
        return Math.max(l, r) + x.val;
    }
}

LeetCode 82. 删除排序链表中的重复元素 II

class Solution {
    public ListNode deleteDuplicates(ListNode head) {
        ListNode hh = new ListNode(0, head), pre = hh, cur = head;
        while(cur != null) {
            ListNode next = cur.next;
            while(next != null && next.val == cur.val) next = next.next;
            if(cur.next == next) pre = cur;
            else pre.next = next;
            cur = next;
        }
        return hh.next;
    }
}

LeetCode 69. x的平方根

简单二分，需要注意，由于涉及到平方计算，int类型可能会溢出，可以强转为long进行比较。一种比较巧妙的做法是，将mid * mid <= x，转化成mid <= x / mid

class Solution {
    public int mySqrt(int x) {
        int l = 0, r = x;
        while(l < r) {
            int mid = l + r + 1 >> 1;
            if(mid <= x / mid) l = mid;
            else r = mid - 1;
        }
        return l;
    }
}

LeetCode 8. 字符串转换整数

简单题，注意溢出的判断，因为每次是乘10再加，判断溢出可以用当前的值和 MAX/10 进行比较

class Solution {
    public int myAtoi(String s) {
        int i = 0, end = s.length() - 1, sign = 1, sum = 0;
        while (i <= end && s.charAt(i) == ' ') i++; // 去除前导空格
        // 判断第一位是否是符号位
        if (i <= end) {
            if (s.charAt(i) == '-') {
                sign = -1;
                i++;
            } else if (s.charAt(i) == '+') i++;
        }
        // 处理每一位
        while (i <= end) {
            int c = s.charAt(i) - '0';
            if (c < 0 || c > 9) break; // 该位置不是数字, 直接结束
            // 是数字, 先判断是否溢出
            if (sign == 1 && (sum > Integer.MAX_VALUE / 10 || (sum == Integer.MAX_VALUE / 10 && c > 7))) return Integer.MAX_VALUE;
            if (sign == -1 && (sum < Integer.MIN_VALUE / 10 || (sum == Integer.MIN_VALUE / 10 && c > 8))) return Integer.MIN_VALUE;
            sum *= 10;
            if (sign == 1) sum += c;
            else sum -= c;
            i++;
        }
        return sum;
    }
}

LeetCode 4. 寻找两个正序数组的中位数

解法一：直接遍历

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int n = nums1.length, m = nums2.length;
        int len = n + m;
        int i = 0, j = 0, l = 0, r = 0;
        for (int k = 0; k <= len / 2; k++) {
            l = r;
            if (i < n && (j >= m || nums1[i] <= nums2[j])) r = nums1[i++];
            else r = nums2[j++];
        }
        if ((len & 1) == 1) return r;
        else return ((double) l + r) / 2;
    }
}

解法二：二分，每次排除一半

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int n = nums1.length, m = nums2.length;
        int len = n + m;
        int l = getKthNum(nums1, 0, nums2, 0, len + 1 >> 1);
        int r = getKthNum(nums1, 0, nums2, 0, len + 2 >> 1);
        return (l + r) / 2.0;
    }

    private int getKthNum(int[] nums1, int i, int[] nums2, int j, int k) {
        int n = nums1.length, m = nums2.length;
        if (i >= n) return nums2[j + k - 1];
        if (j >= m) return nums1[i + k - 1];
        if (k == 1) return Math.min(nums1[i], nums2[j]);
        int mid = k / 2;
        int ie = Math.min(i + mid - 1, n - 1);
        int je = Math.min(j + mid - 1, m - 1);
        if (nums1[ie] <= nums2[je]) return getKthNum(nums1, ie + 1, nums2, j, k - (ie - i + 1));
        else return getKthNum(nums1, i, nums2, je + 1, k - (je - j + 1));
    }
}

LeetCode.151 翻转字符串里的单词

解法一：手动模拟（Java由于String是不可变的，所以需要额外空间，C++的string是可变的，可以原地翻转）

1. 去除首尾空格，trim
2. 整体翻转
3. 翻转每个单词

class Solution {
    public String reverseWords(String s) {
        StringBuilder sb = trim(s);
        reverse(sb, 0, sb.length() - 1);
        reverseWords(sb);
        return sb.toString();
    }

    private StringBuilder trim(String s) {
        StringBuilder sb = new StringBuilder();
        int begin = 0, end = s.length() - 1;
        while (begin <= end && s.charAt(begin) == ' ') begin++;
        while (begin <= end && s.charAt(end) == ' ') end--;
        while (begin <= end) {
            if (s.charAt(begin) != ' ') sb.append(s.charAt(begin));
            else if (sb.charAt(sb.length() - 1) != ' ') sb.append(' ');
            begin++;
        }
        return sb;
    }

    private void reverse(StringBuilder sb, int begin, int end) {
        while (begin < end) {
            char t = sb.charAt(begin);
            sb.setCharAt(begin, sb.charAt(end));
            sb.setCharAt(end, t);
            begin++;
            end--;
        }
    }

    private void reverseWords(StringBuilder sb) {
        int begin = 0;
        for (int i = 0; i <= sb.length(); i++) {
            if (i == sb.length() || sb.charAt(i) == ' ') {
                reverse(sb, begin, i - 1);
                begin = i + 1;
            }
        }
    }
}

解法二：借助栈
按顺序从前到后遍历，将每个单词压入栈，最后依次从栈中弹出单词

class Solution {
    public String reverseWords(String s) {
        Deque<String> stack = new LinkedList<>();
        int begin = 0, end = 0;
        while (end < s.length()) {
            while (begin < s.length() && s.charAt(begin) == ' ') begin++; // 找到单词起点
            if (begin >= s.length()) break; // 起点越界
            end = begin + 1;
            while (end < s.length() && s.charAt(end) != ' ') end++;
            stack.push(s.substring(begin, end));
            begin = end;
        }
        StringBuilder sb = new StringBuilder();
        while (!stack.isEmpty()) {
            sb.append(stack.pop());
            sb.append(' ');
        }
        sb.deleteCharAt(sb.length() - 1);
        return sb.toString();
    }
}

105. 从前序和中序遍历序列构造二叉树

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int x = 0;
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        return build(preorder, inorder, 0, inorder.length - 1);
    }

    private TreeNode build(int[] pre, int in[], int i, int j) {
        if (i > j) return null;
        int root = pre[x++]; // 取出当前的根节点
        // 在中序遍历中寻找根节点的位置
        int k = i;
        while(k <= j) {
            if (in[k] == root) break;
            k++;
        }
        TreeNode node = new TreeNode(root);
        // 递归求解左右子节点
        TreeNode left = build(pre, in, i, k - 1);
        TreeNode right = build(pre, in, k + 1, j);
        node.left = left;
        node.right = right;
        return node;
    }
}

更易懂的递归

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        return build(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1);
    }

    private TreeNode build(int[] pre, int pl, int pr, int[] in, int il, int ir) {
        if (pl > pr) return null;
        int root = pre[pl];
        int k = il;
        for (;k <= ir; k++) {
            if (in[k] == root) break;
        }
        TreeNode node = new TreeNode(root);
        int llen = k - il;
        int rlen = ir - k;
        TreeNode left = build(pre, pl + 1, pl + llen, in, il, k - 1);
        TreeNode right = build(pre, pl + llen + 1, pr, in, k + 1, ir);
        node.left = left;
        node.right = right;
        return node;
    }
}

76. 最小覆盖子串

滑动窗口

class Solution {
    public String minWindow(String s, String t) {
        Map<Character, Integer> needMap = new HashMap<>();
        for (int i = 0; i < t.length(); i++) {
            char c = t.charAt(i);
            needMap.put(c, needMap.getOrDefault(c, 0) + 1);
        }
        int needCnt = t.length();
        int i = 0, j = 0;
        int begin = 0, end = 0;
        int len = Integer.MAX_VALUE;
        while (j < s.length()) {
            while (needCnt > 0 && j < s.length()) {
                char c = s.charAt(j);
                if (needMap.containsKey(c)) {
                    if (needMap.get(c) > 0) needCnt--;
                    needMap.put(c, needMap.get(c) - 1);
                }
                j++;
            }
            if (needCnt > 0) break;

            while (true) {
                char c = s.charAt(i);
                if (needMap.containsKey(c)) {
                    if (needMap.get(c) == 0) break;
                    needMap.put(c, needMap.get(c) + 1);
                }
                i++;
            }
            if (len > j - i) {
                len = j - i;
                begin = i;
                end = j;
            }
            
            char c = s.charAt(i);
            needMap.put(c, needMap.get(c) + 1);
            needCnt++;
            i++;
        }
        return s.substring(begin, end);
    }
}

31. 下一个排列

多列几个数组，进行观察。可以发现规律。
需要从数组末尾往前找，找到逆序的最大长度。
比如1, 4, 2, 5, 3, 1，那末尾的逆序的最大长度就是 5, 3, 1
那么需要将前一个数2，变大。则在后面逆序子数组中，找到第一个比2大的数，与2交换，并且把逆序子数组，从小到大排列（做一次逆序）。
先是2和3交换，变成了 1, 4, 3, 5, 2, 1，然后对后面的逆序数组进行翻转，变成了1, 4, 3, 1, 2, 5

class Solution {
    public void nextPermutation(int[] nums) {
        int last = nums.length - 1;
        int first = last - 1;
        while (first >= 0 && first + 1 <= last) {
            if (nums[first] >= nums[first + 1]) first--;
            else break;
        }
        if (first >= 0) {
            // 在逆序序列中找到第一个比这个数大的, 并交换之
            int i = first + 1;
            while (i <= last) {
                if (i == last || nums[i + 1] <= nums[first]) break;
                i++;
            }
            int t = nums[first];
            nums[first] = nums[i];
            nums[i] = t;
        }

        // 对 first + 1 到 last 进行逆序
        int i = first + 1, j = last;
        while (i < j) {
            int t = nums[i];
            nums[i] = nums[j];
            nums[j] = t;
            i++;
            j--;
        }
    }
}

239. 滑动窗口的最大值

单调队列的简单应用

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        int n = nums.length;
        int[] res = new int[n - k + 1];
        int resIndex = 0;
        int[] queue = new int[n];
        int hh = 0, tt = -1; // 队头和队尾
        for (int i = 0, j = 0; j < n; j++) {
            while (tt >= hh && nums[queue[tt]] <= nums[j]) tt--;
            queue[++tt] = j;
            if (j - queue[hh] + 1 > k) hh++;
            if (j >= k - 1) res[resIndex++] = nums[queue[hh]];
        }
        return res;
    }
}

104. 二叉树的最大深度

考察二叉树的遍历，用dfs或bfs均可，遍历时额外维护深度这个属性

class Solution {
    int ans = 0;
    public int maxDepth(TreeNode root) {
        dfs(root, 1);
        return ans;
    }
    private void dfs(TreeNode x , int d) {
        if (x == null) return;
        if (d > ans) ans = d;
        dfs(x.left, d + 1);
        dfs(x.right, d + 1);
    }
}

129. 求根节点到叶节点数字之和

简单dfs，可以考虑用一个path数组，来存dfs过程中的节点路径，并在到达叶节点时，就认为找到一个数字，将当前path表示的路径所对应的数字，累加到答案上。
也可以采用另一种思路，每个节点会对其子节点有一个贡献值，子节点只需要拿到父节点的贡献值 × 10 ，再加上自己节点的值，就得到自己的贡献值。若已经是子节点，就将自身的贡献值直接加到答案上，否则将自己的贡献值，通过dfs传递给自己的子节点。

class Solution {
    int ans = 0;
    public int sumNumbers(TreeNode root) {
        dfs(root, 0);
        return ans;
    }

    private void dfs(TreeNode x, int base) {
        int newBase = base * 10 + x.val;
        if (x.left == null && x.right == null) {
            ans += newBase;
            return;
        }
        if (x.left != null) dfs(x.left, newBase);
        if (x.right != null) dfs(x.right, newBase);
    }
}

41. 缺失的第一个正整数

要求$O(n)$的时间复杂度和常数级的空间复杂度。

解法一：原地哈希

对于长度为n的数组，缺失的最小正整数，要么在[1, n] 内，要么是n + 1。我们对出现过的正整数，在对应的下标的位置，打上标记，表示该下标对应的正数，出现过（将该下标位置的数置为负）。那么我们数组初始时，必须全为正数。那么原数组中本身存在的负数，由于不会对打标记起到任何作用，我们可以将其置为任意一个大于n的正数，比如n + 1。打完标记后，只需要遍历数组，找到第一个不为负数的位置，则说明该下标位置对应的正数，没有出现过。实际运算次数是 3n

class Solution {
    public int firstMissingPositive(int[] nums) {
        int n = nums.length;
        for (int i = 0; i < n; i++) {
            if (nums[i] <= 0) nums[i] = n + 1;
        }
        for (int i = 0; i < n; i++) {
            int c = Math.abs(nums[i]);
            if (c <= n && nums[c - 1] > 0) nums[c - 1] = -nums[c - 1]; // 已经为负的, 表示已打过标记, 不重复打
        }
        for (int i = 0; i < n; i++) {
            if (nums[i] > 0) return i + 1;
        }
        return n + 1;
    }
}

解法二：交换法
与解法一类似，关键在于如何表示某个正整数出现过。
这个思路是，将正整数，交换到其对应的位置上。比如将数字2，交换到数组中第2个位置的地方（下标为1的位置）。
交换完毕后，所有出现过的正整数，都与其下标一致。只需要遍历一次数组，找到第一个元素值与下标不一致的，其下标就是缺失的第一个正数。交换最多需要n次，遍历一次n，运算次数为2n。

class Solution {
    public int firstMissingPositive(int[] nums) {
        int n = nums.length;
        // 众神归位
        for (int i = 0; i < n; i++) {
            while (nums[i] > 0 && nums[i] <= n) {
                int pos = nums[i] - 1;
                // 交换 i 和 pos
                if (nums[i] == nums[pos]) break; // 已经在对应位置
                int t = nums[i];
                nums[i] = nums[pos];
                nums[pos] = t;
            }
        }
        // 找第一个
        for (int i = 0; i < n; i++) {
            if (nums[i] != i + 1) return i + 1;
        }
        return n + 1;
    }
}

22. 括号生成

dfs + 剪枝

下面第一个写法可以通过，是因为java中的String是不可变对象，每次用+做字符串拼接，生成的都是一个新的对象，所以在dfs回溯时不需要恢复现场。
为了更好的表示dfs和回溯的思想，另写一版使用StringBuilder的代码。

class Solution {
    public List<String> generateParenthesis(int n) {
        List<String> ans = new ArrayList<>();
        dfs("", n, n, ans);
        return ans;
    }

	/**
	* left 是剩余的可用的左括号数量, right 同理
	**/
    private void dfs(String s, int left, int right, List<String> ans) {
        if (left == 0 && right == 0) {
            ans.add(s);
            return ;
        }
        if (left > right) return ; // 当剩余左括号数量 大于 右括号, 剪枝
        if (left > 0) dfs(s + "(", left - 1, right, ans);
        if (right > 0) dfs(s + ")", left, right - 1, ans);
    }
}

class Solution {
    public List<String> generateParenthesis(int n) {
        List<String> ans = new ArrayList<>();
        dfs(new StringBuilder(), n, n, ans);
        return ans;
    }

    private void dfs(StringBuilder sb, int left, int right, List<String> ans) {
        if (left == 0 && right == 0) {
            ans.add(sb.toString());
            return ;
        }
        if (left > right) return ;
        if (left > 0) {
            sb.append('(');
            dfs(sb, left - 1, right, ans);
            sb.deleteCharAt(sb.length() - 1); // 恢复现场
        }
        if (right > 0) {
            sb.append(')');
            dfs(sb, left, right - 1, ans);
            sb.deleteCharAt(sb.length() - 1); // 恢复现场
        }
    }
}

110. 平衡二叉树

dfs求每个节点的高度即可

class Solution {
    boolean ans = true;
    public boolean isBalanced(TreeNode root) {
        return dfs(root) >= 0;
    }

    /**
    * @return -1 表示不平衡, 其他值表示当前节点高度
    **/
    private int dfs(TreeNode x) {
        if (x == null) return 0;
        int lh = dfs(x.left), rh = dfs(x.right);
        if (lh == -1 || rh == -1 || Math.abs(lh - rh) > 1) return -1;
        return Math.max(lh, rh) + 1;
    }
}

155. 最小栈

解法一：辅助栈，额外空间复杂度 $O(n)$

class MinStack {
    Deque<Integer> stack;
    Deque<Integer> min;
    public MinStack() {
        stack = new LinkedList<>();
        min = new LinkedList<>();
    }
    
    public void push(int val) {
        stack.push(val);
        if (min.isEmpty() || min.peek() > val) min.push(val);
        else min.push(min.peek());
    }
    
    public void pop() {
        stack.pop();
        min.pop();
    }
    
    public int top() {
        return stack.peek();
    }
    
    public int getMin() {
        return min.peek();
    }
}

解法二：差值法，额外空间复杂度$O(1)$
用一个栈，加一个min。栈中存的是原值和当前min的差值。
关键的点在于，可以依靠栈中存放的差值，和min，还原出原值，并在pop时，能还原出上一个min的值。

初始时，栈为空。假设push一个x1进来，则栈中存0，min为x1。
第二次push一个x2进来，栈中存x2 - min，若x2 < min，则更新min = x2。

当pop时，若栈顶元素小于0，说明当前元素就是最小值，即当前元素为min，在弹出当前元素后，需要将min还原为上一个值，则更新min = min - 栈顶元素。若栈顶元素大于0，说明当前元素比min大，则当前元素为栈顶元素+ min，且pop后min不变，无需更新。

class MinStack {

    Deque<Long> stack; // x - min
    long min;
    
    public MinStack() {
        stack = new LinkedList<>();
    }
    
    public void push(int val) {
        if (stack.isEmpty()) {
            min = val;
            stack.push(0L);
        } else {
            long d = val - min;
            stack.push(d);
            min = Math.min(min, val);
        }
    }
    
    public void pop() {
        long c = stack.peek();
        stack.pop();
        if (c < 0) min = min - c; 
    }
    
    public int top() {
        long c = stack.peek();
        if (c < 0) return (int) min;
        return (int) (c + min);
    }
    
    public int getMin() {
        return (int) min;
    }
}

112. 路径总和

简单dfs

class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if (root == null) return false;
        if (root.left == null && root.right == null) return targetSum == root.val;
        boolean left = hasPathSum(root.left, targetSum - root.val);
        boolean right = hasPathSum(root.right, targetSum - root.val);
        return left || right;
    }
}

113. 路径总和II

class Solution {
    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        List<List<Integer>> ans = new ArrayList<>();
        List<Integer> path = new ArrayList<>();
        dfs(root, targetSum, path, ans);
        return ans;
    }

    private void dfs(TreeNode x, int sum, List<Integer> path, List<List<Integer>> ans) {
        if (x == null) return;
        path.add(x.val);
        if (x.left == null && x.right == null && sum == x.val) ans.add(new ArrayList<>(path));
        dfs(x.left, sum - x.val, path, ans);
        dfs(x.right, sum - x.val, path, ans);
        path.remove(path.size() - 1);
    }
}

98. 验证二叉搜索树

class Solution {
    public boolean isValidBST(TreeNode root) {
        boolean left = check(root.left, Long.MIN_VALUE, root.val);
        boolean right = check(root.right, root.val, Long.MAX_VALUE);
        return left && right;
    }

    private boolean check(TreeNode x, long low, long high) {
        if (x == null) return true;
        if (x.val <= low || x.val >= high) return false;
        boolean left = check(x.left, low, x.val);
        boolean right = check(x.right, x.val, high);
        return left && right;
    }
}

543. 二叉树的直径

dfs，以每个点为中继点，经过这个点的最长路径，就是其左儿子能往下走的最长长度（左子树的深度），以及其右儿子能往下走的最长长度（右儿子的深度），两者之和。
只要将每个点看作中继节点，求出每个经过这个中继节点的最长长度，再求一个max即可。
（这题的分级是easy，但我感觉应该算个medium）

class Solution {
    int ans = 0;
    public int diameterOfBinaryTree(TreeNode root) {
        dfs(root);
        return ans;
    }

    private int dfs(TreeNode x) {
        if (x == null) return 0;
        int l = dfs(x.left), r = dfs(x.right);
        ans = Math.max(ans, l + r);
        return Math.max(l, r) + 1;
    }
}

43. 字符串相乘

解法一：模拟竖式乘法，耗时12ms

class Solution {
    public String multiply(String num1, String num2) {
        List<Integer> ans = new ArrayList<>();
        for (int i = num2.length() - 1; i >= 0; i--) {
            List<Integer> one = new ArrayList<>();
            for (int j = num2.length() - 1; j > i; j--) one.add(0);
            int c = 0;
            for (int j = num1.length() - 1; j >= 0; j--) {
                c += (num2.charAt(i) - '0') * (num1.charAt(j) - '0');
                one.add(c % 10);
                c /= 10;
            }
            if (c > 0) one.add(c);

            // 加和
            int x = 0, y = 0;
            c = 0;
            while (x < ans.size() && y < one.size()) {
                c += one.get(y) + ans.get(x);
                ans.set(x, c % 10);
                c /= 10;
                x++;
                y++;
            }
            while (y < one.size()) {
                c += one.get(y);
                ans.add(c % 10);
                c /= 10;
                y++;
            }
            if (c > 0) ans.add(c);
        }
        // 去掉前导0
        while (ans.get(ans.size() - 1) == 0 && ans.size() > 1) ans.remove(ans.size() - 1);
        // 转换为String
        StringBuilder sb = new StringBuilder();
        for (int i = ans.size() - 1; i >= 0; i--) {
            char ch = (char) ('0' + ans.get(i));
            sb.append(ch);
        }
        return sb.toString();
    }
}

解法二：直接相乘，耗时3ms

class Solution {
    public String multiply(String num1, String num2) {
        int n = num1.length(), m = num2.length();
        int[] ans = new int[n + m];
        for (int i = n - 1; i >= 0; i--) {
            int x1 = num1.charAt(i) - '0';
            for (int j = m - 1; j >= 0; j--) {
                int x2 = num2.charAt(j) - '0';
                ans[i + j + 1] += x1 * x2;
                ans[i + j] += ans[i + j + 1] / 10;
                ans[i + j + 1] = ans[i + j + 1] % 10;
            }
        }
        StringBuilder sb = new StringBuilder();
        int i = 0;
        while (i < n + m - 1 && ans[i] == 0) i++;
        while (i < n + m) sb.append(ans[i++]);
        return sb.toString();
    }
}

78. 子集

每个位置的数，都有选或者不选两种方案。
简单dfs，注意回溯时要恢复现场即可

class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> ans = new ArrayList<>();
        List<Integer> one = new ArrayList<>();
        dfs(0, nums, one, ans);
        return ans;
    }

    private void dfs(int x, int[] nums, List<Integer> one, List<List<Integer>> ans) {
        if (x == nums.length) {
            ans.add(new ArrayList<>(one));
            return ;
        }
        // 不选
        dfs(x + 1, nums, one, ans);
        // 选
        one.add(nums[x]);
        dfs(x + 1, nums, one, ans);
        one.remove(one.size() - 1);
    }
}

470. 用 rand7() 实现 rand10()

贴一个牛逼的万能题解（可以用rand7() 实现 randx()）：点这里

核心思想是扩大区间范围，首先让区间能覆盖1-10，然后再考虑如何做映射，让每个数字的概率相等。
怎么扩大区间范围呢，很简单的想法就是多次调用rand7()，并做加法（也可以做乘法，但本质上都是做乘法，比如我们调了2次rand7()，我们实际取的是两次数字的组合）。我的初始解法就是调用5次，并作相加，再取余映射到1-10，但每个数字的概率只能近似相等。实际还有更好的方法，只需要调用2次rand7()即可

我的题解

// 我的解法, 9ms
class Solution extends SolBase {
    public int rand10() {
        int sum = rand7() + rand7() + rand7() + rand7() + rand7();
        return 1 + (sum + 9) % 10;
    }
}

官方题解（保证概率绝对相等）

调用2次，组合起来就是一个 7 × 7 的矩阵, 每种组合的概率都是1/49， 只取前 40, 并映射到 1-10，对于 41 - 49, 拒绝，拒绝的概率为 9/49

class Solution extends SolBase {
    public int rand10() {
        int r, c, idx;
        do {
            r = rand7();
            c = rand7();
            idx = (r - 1) * 7 + c;
        } while(idx > 40);
        return 1 + (idx - 1) % 10;
    }
}

更好的题解（from上方的链接）

调用两次rand7，分别构造1/2和1/5的概率即可。
第一次调用，取1-6，拒绝7，按照奇偶分组，分为2组，构造出1/2的概率。
第二次调用，取1-5，拒绝6-7，每个数字单独为一个组，共5组，构造出1/5的概率。
两次组合就能构造出1/10。
拒绝的概率为 1/7 × 2/7 = 2/49

class Solution extends SolBase {
    public int rand10() {
        int first, second;
        do first = rand7(); while (first > 6);
        do second = rand7(); while (second > 5);
        return (first & 1) * 5 + second;
    }
}

（这种思路比较通用，可以解决用 rand_7 构造 rand_n）
比如想用 rand7 构造 rand11
同样是调用2次，第一次同样按奇偶分为2组，构造出1/2；第二次取1-6，拒绝7，分为6组，构造出1/6；两次组合就能组合出12组，拒绝掉最后一组，只取前11组即可。

再比如，想用rand7 构造 rand14
我们将14拆成2个数的乘积（2个数都在1-7范围内），则可以拆成 2×7
则调用2次，第一次取1-6，拒绝7，按奇偶分为2组；第二次取1-7，共7组；两次组合就是14组。

比如 rand7 构造 rand19
我们取 大于19的数，拆成2个数（2个数都在1-7内）的乘积，则 20 = 4 × 5
调用2次，第一次取1-4，拒绝5-7，4组；第二次取1-5，拒绝6-7，5组。也可以 20 = 2 × 10；10按照上面构造rand10 的方式来，一共需要调3次。

101. 对称二叉树

不能简单地用dfs或者bfs来做了。
之前自己的错误解法有：用bfs遍历每一层，保证每一层的序列都是回文（无法区分左右子节点的差异）。比如下图

正确做法：写一个函数，判断2个子树是否是镜像，然后递归的调用即可（下面借一下官方题解）

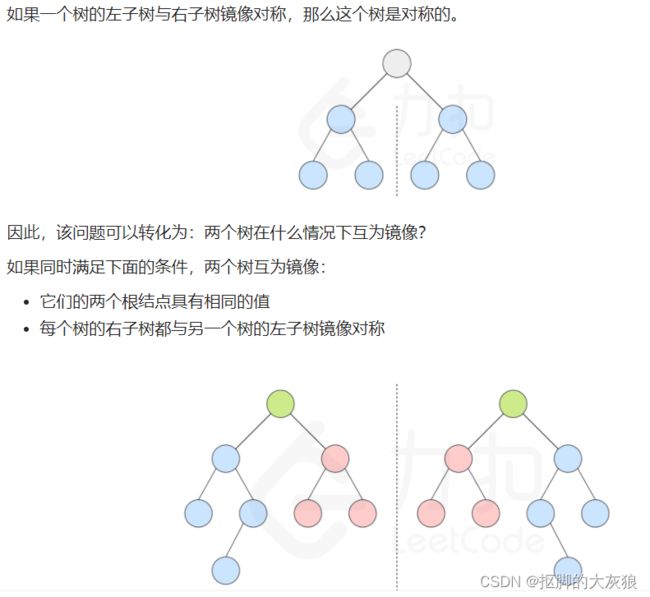
class Solution {
    public boolean isSymmetric(TreeNode root) {
        if (root == null) return true;
        return check(root.left, root.right);
    }

    private boolean check(TreeNode l, TreeNode r) {
        if (l == null && r == null) return true;
        if (l == null || r == null) return false;
        if (l.val != r.val) return false;
        return check(l.right, r.left) && check(l.left, r.right);
    }
}

同样的，上述递归写法也可以改成迭代，用一个队列来模拟即可

    public boolean isSymmetric(TreeNode root) {
        Deque<TreeNode> queue = new LinkedList<>();
        queue.offer(root.left);
        queue.offer(root.right);
        boolean ans = true;
        while (!queue.isEmpty()) {
            TreeNode l = queue.poll();
            TreeNode r = queue.poll();
            if (l == null && r == null) continue;
            if (l == null || r == null || l.val != r.val) {
                ans = false;
                break;
            }
            queue.offer(l.left);
            queue.offer(r.right);
            queue.offer(l.right);
            queue.offer(r.left);
        }
        return ans;
    }
}

64. 最小路径和

朴素动规

class Solution {
    public int minPathSum(int[][] grid) {
        int n = grid.length, m = grid[0].length;
        int[][] f = new int[n + 1][m + 1];
        for (int i = 1; i <= m; i++) f[1][i] = f[1][i - 1] + grid[0][i - 1];
        for (int i = 1; i <= n; i++) f[i][1] = f[i - 1][1] + grid[i - 1][0];
        for (int i = 2; i <= n; i++) {
            for (int j = 2; j <= m; j++) {
                f[i][j] = Math.min(f[i][j - 1], f[i - 1][j]) + grid[i - 1][j - 1];
            }
        }
        return f[n][m];
    }
}

用滚动数组的思想进行优化

class Solution {
    public int minPathSum(int[][] grid) {
        int n = grid.length, m = grid[0].length;
        int[] ans = new int[m + 1];
        for (int i = 1; i <= m; i++) ans[i] = ans[i - 1] + grid[0][i - 1];
        for (int i = 2; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                if (j == 1) ans[j] += grid[i - 1][0];
                else ans[j] = Math.min(ans[j - 1], ans[j]) + grid[i - 1][j - 1];
            }
        }
        return ans[m];
    }
}

322. 零钱兑换

动规，解题思路类似完全背包。
我的解法：耗时22ms，有点拉跨，晚点看下官方题解有无更优的解法

class Solution {
    public int coinChange(int[] coins, int m) {
        if (m == 0) return 0;
        // f(i,j) = min{ f(i-1,j), f(i,j-a)+1 }
        int n = coins.length;
        int[][] f = new int[n + 1][m + 1];
        // initiation
        for (int i = 0; i <= n; i++) {
            for (int j = 0; j <= m; j++) {
                f[i][j] = j == 0 ? 0 : -1;
            }
        }
        // calculate
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                int a = coins[i - 1];
                if (f[i - 1][j] == -1) {
                    if (j >= a && f[i][j - a] != -1) f[i][j] = f[i][j - a] + 1;
                } else {
                    f[i][j] = f[i - 1][j];
                    if (j >= a && f[i][j - a] != -1) f[i][j] = Math.min(f[i][j], f[i][j - a] + 1);
                }
            }
        }
        return f[n][m];
    }
}

只需要一维dp即可，14ms
F(s) 表示组成金额S需要的最少硬币数量

class Solution {
    public int coinChange(int[] coins, int amount) {
        int[] f = new int[amount + 1];
        Arrays.fill(f, -1);
        f[0] = 0;
        for (int i = 1; i <= amount; i++) {
            int min = Integer.MAX_VALUE;
            for (int c : coins) {
                if (i >= c && f[i - c] >= 0) min = Math.min(min, f[i - c] + 1);
            }
            if (min != Integer.MAX_VALUE) f[i] = min;
        }
        return f[amount];
    }
}

718. 最长重复子数组

先想个暴力解法，随后尝试对其进行优化

暴力解法：$O(n^3)$

public int findLength(int[] nums1, int[] nums2) {
        int ans = 0;
        for (int i = 0; i < nums1.length; i++) {
            for (int j = 0; j < nums2.length; j++) {
                int k = 0;
                while (i + k < nums1.length && j + k < nums2.length && nums1[i + k] == nums2[j + k]) k++;
                ans = Math.max(ans, k);
            }
        }
        return ans;
    }

解法一：动态规划

a[i]和b[j]，会被重复比较，最坏情况下，会被重复比较min(i + 1,j + 1)次。我们希望优化，使得a[i]和b[j]都最多被比较一次。设f[i][j]为以a[i]和b[j]为起始位置的最长公共前缀。我们发现，当a[i] == b[j] 时，那么f[i][j] = f[i + 1][j + 1] + 1，所以我们可以用动态规划的思想，从后往前进行状态转移的计算。
时间复杂度 $O(N\times M)$，空间复杂度$O(N\times M)$

class Solution {
    public int findLength(int[] a, int[] b) {
        int n = a.length, m = b.length;
        int[][] f = new int[n + 1][m + 1];
        int ans = 0;
        for (int i = n - 1; i >= 0 ; i--) {
            for (int j = m - 1; j >= 0 ; j--) {
                if (a[i] == b[j]) f[i][j] = f[i + 1][j + 1] + 1;
                ans = Math.max(ans, f[i][j]);
            }
        }
        return ans;
    }
}

解法二：滑动窗口

动图来自这里

class Solution {
    public int findLength(int[] a, int[] b) {
        int n = a.length, m = b.length;
        int total = n + m - 1;
        int ans = 0;
        int aBegin = 0, bBegin = 0, len = 0;
        for (int i = 0; i < total; i++) {
            if (i < m) {
                aBegin = 0;
                bBegin = m - 1 - i;
                len = Math.min(n, i + 1);
            } else {
                aBegin = i - m + 1;
                bBegin = 0;
                len = Math.min(m, n - aBegin);
            }
            ans = Math.max(ans, maxCommon(a, b, aBegin, bBegin, len));
        }
        return ans;
    }
    
    private int maxCommon(int[] a, int[] b, int aBegin, int bBegin, int len) {
        int c = 0, ans = 0;
        for (int i = 0; i < len; i++) {
            if (a[aBegin + i] == b[bBegin + i]) c++;
            else c = 0;
            ans = Math.max(ans, c);
        }
        return ans;
    }
}

48. 旋转图像

第(i, j) 个位置，旋转后的新位置是 (j , n - i - 1)，原地旋转，每次交换4个位置的数

class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        for (int i = 0; i < n / 2; ++i) {
            for (int j = 0; j < (n + 1) / 2; ++j) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n - j - 1][i];
                matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
                matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
                matrix[j][n - i - 1] = temp;
            }
        }
    }
}

169. 多数元素

这是一道Easy，但有很巧妙的做法

解法一：简单计数，借用Map，这里省略不写

解法二：排序后，直接取中间值（时间复杂度$O(nlogn)$，空间复杂度$O(1)$）

class Solution {
    public int majorityElement(int[] nums) {
        // 手写快排, 也可以直接调用Arrays.sort
        quickSort(nums, 0, nums.length - 1); 
        return nums[nums.length / 2];
    }

    private void quickSort(int[] nums, int l, int r) {
        if (l >= r) return;
        int x = nums[l + r >> 1], i = l - 1, j = r + 1;
        while (i < j) {
            do i++; while(nums[i] < x);
            do j--; while(nums[j] > x);
            if (i < j) {
                int t = nums[i];
                nums[i] = nums[j];
                nums[j] = t;
            }
        }
        quickSort(nums, l, j);
        quickSort(nums, j + 1 , r);
    }
}

解法三：摩尔投票。

基本思路：如果我们把众数记为 +1，把其他数记为 −1，将它们全部加起来，显然和大于 0，从结果本身我们可以看出众数比其他数多。

设两个变量candidate，count。初始化count = 0。遍历数组，先判断count是否等于0.若count=0，则先把当前数组元素赋值给candidate。再进行如下判断

• 若candidate 等于当前数组元素，则count + 1
• 若不等，则count - 1

最后的candidate就是众数。

由于众数出现的个数大于一半，而只有当count被减到0时，candidate才会被更换。所以最后留下的candidate就是众数

class Solution {
    public int majorityElement(int[] nums) {
        int candidate = 0, count = 0;
        for (int x : nums) {
            if (count == 0) candidate = x; // count 被减到0, 更换candidate
            if (candidate == x) count++;
            else count--;
        }
        return candidate;
    }
}

165. 比较版本号

简单模拟即可

朴素做法（不使用内置api）

class Solution {
    public int compareVersion(String version1, String version2) {
        int n = version1.length(), m = version2.length();
        int i = 0, j = 0;
        while (i < n || j < m) {
            int v1 = 0, v2 = 0;
            while (i < n && version1.charAt(i) != '.') v1 = v1 * 10 + version1.charAt(i++) - '0';
            while (j < m && version2.charAt(j) != '.') v2 = v2 * 10 + version2.charAt(j++) - '0';
            if (v1 > v2) return 1;
            if (v1 < v2) return -1;
            i++;
            j++;
        }
        return 0;
    }
}

226. 翻转二叉树

简单递归

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) return null;
        TreeNode left = invertTree(root.left), right = invertTree(root.right);
        root.left = right;
        root.right = left;
        return root;
    }
}

迭代：BFS(层序遍历)

class Solution {
    public TreeNode invertTree(TreeNode root) {
       Queue<TreeNode> queue = new LinkedList<>();
       if(root != null) queue.offer(root);
       while (!queue.isEmpty()) {
           TreeNode x = queue.poll();
           TreeNode t = x.left;
           x.left = x.right;
           x.right = t;
           if (x.left != null) queue.offer(x.left);
           if (x.right != null) queue.offer(x.right);
       }
       return root;
    }
}

迭代：DFS

class Solution {
    public TreeNode invertTree(TreeNode root) {
       Deque<TreeNode> stack = new LinkedList<>();
       if (root != null) stack.push(root);
       while (!stack.isEmpty()) {
           TreeNode x = stack.pop();
           TreeNode t = x.left;
           x.left = x.right;
           x.right = t;
           if (x.left != null) stack.push(x.left);
           if (x.right != null) stack.push(x.right);
       }
       return root;
    }
}

26. 删除有序数组中的重复元素

class Solution {
    public int removeDuplicates(int[] nums) {
        if (nums == null || nums.length == 0) return 0;
        int last = 1, prev = nums[0];
        for (int i = 1; i < nums.length; i++) {
            if (nums[i] == prev) continue; // 重复
            nums[last++] = nums[i];
            prev = nums[i];
        }
        return last;
    }
}

221. 最大正方形

解法一：动态规划
朴素版

class Solution {
    public int maximalSquare(char[][] matrix) {
        int n = matrix.length;
        int m = matrix[0].length;
        int ans = 0;
        int[][] f = new int[n + 1][m + 1];
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m ; j++) {
                if (matrix[i - 1][j - 1] == '0') continue;
                f[i][j] = Math.min(f[i][j - 1], f[i - 1][j]);
                f[i][j] = Math.min(f[i][j], f[i - 1][j - 1]) + 1;
                ans = Math.max(ans, f[i][j]);
            }
        }
        return ans * ans;
    }
}

滚动数组优化

class Solution {
    public int maximalSquare(char[][] matrix) {
        int n = matrix.length;
        int m = matrix[0].length;
        int ans = 0;
        int[] f = new int[m + 1];
        for (int i = 1; i <= n; i++) {
            int northWest = 0;
            for (int j = 1; j <= m ; j++) {
                int nextNorthWest = f[j];
                f[j] = Math.min(Math.min(f[j - 1], f[j]), northWest) + 1;
                if (matrix[i - 1][j - 1] == '0') f[j] = 0;
                ans = Math.max(ans, f[j]);
                northWest = nextNorthWest;
            }
        }
        return ans * ans;
    }
}

解法二：二进制（将相邻的两行做按位与操作），枚举所有i，j的组合

TODO

240. 搜索二维矩阵II

我的解法：二分+递归

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int n = matrix.length;
        int m = matrix[0].length;
        // 二维二分
        // 设置二分的边界
        // (li, lj) 到左上角 皆为不可选区域
        // (ri, rj) 到右下角 皆为不可选区域
        return binarySearch(matrix, target, 0, 0, n - 1, m - 1);
    }

    private boolean binarySearch(int[][] m, int target, int li, int lj, int ri, int rj) {
        if (li > ri || lj > rj) return false; // 没有可搜索的地方了
        if (li == ri && lj == rj) return target == m[li][lj]; // 最后一个地方
        
        if (li == ri) {
            // 同一行, 直接二分
            while (lj < rj) {
                int mid = lj + rj >> 1;
                if (m[li][mid] < target) lj = mid + 1;
                else rj = mid;
            }
            return m[li][lj] == target;
        }

        if (lj == rj) {
            // 同一列, 直接二分
            while (li < ri) {
                int mid = li + ri >> 1;
                if (m[mid][lj] < target) li = mid + 1;
                else ri = mid;
            }
            return m[li][lj] == target;
        }

        // 否则, 斜着二分
        int mi = li + ri >> 1;
        int mj = lj + rj >> 1;
        // 获取中点
        if (target == m[mi][mj]) return true; // 找到了提前返回
        if (target > m[mi][mj]) {
            // 中点的位置比 target 小, 递归地搜索两块区域
            return binarySearch(m, target, mi + 1, lj, ri, rj) || binarySearch(m, target, li, mj + 1, mi, rj);
        } else {
            // 中点的位置比 target 大, 递归地搜索两块区域
            return binarySearch(m, target, li, lj, mi - 1, rj) || binarySearch(m, target, mi, lj, ri, mj - 1);
        }
    }
}