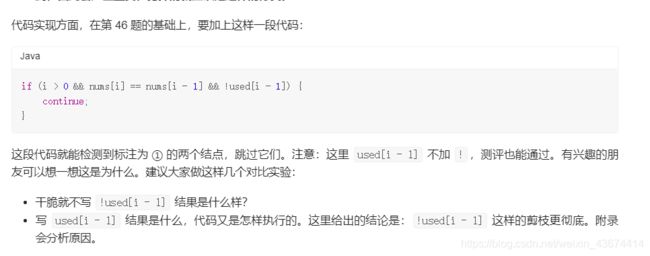
Leetcode_入门_回溯
Leetcode_入门_回溯
- Backtracking(回溯)
-
- 1、电话号码的字母组合(17、Medium)
-
- 1)题目要求
- 2)我的解法
- 3)其他解法
- 4)自己的优化代码
- 5)学到的东西
- 2、 复原IP地址(93、Medium)
-
- 1)题目要求
- 2)我的解法
- 3)其他解法
- 4)自己的优化代码
- 5)学到的东西
- 3、单词搜索(79、Medium)
-
- 1)题目要求
- 2)我的解法
- 3)其他解法
- 4)自己的优化代码
- 5)学到的东西
- 4、 二叉树的所有路径(257、Easy)
-
- 1)题目要求
- 2)我的解法
- 3)其他解法
- 4)自己的优化代码
- 5)学到的东西
- 5、 全排列(46、Medium)
-
- 1)题目要求
- 2)我的解法
- 3)其他解法
- 4)自己的优化代码
- 5)学到的东西
- 6、全排列 II(47、Medium)
-
- 1)题目要求
- 2)我的解法
- 3)其他解法
- 4)自己的优化代码
- 5)学到的东西
- 7、组合(77、Medium)
-
- 1)题目要求
- 2)我的解法
- 3)其他解法
- 4)自己的优化代码
- 5)学到的东西
- 8、组合总和(39、Medium)
-
- 1)题目要求
- 2)我的解法
- 3)其他解法
- 4)自己的优化代码
- 5)学到的东西
- 9、组合总和 II(40、Medium)
-
- 1)题目要求
- 2)我的解法
- 3)其他解法
- 4)自己的优化代码
- 5)学到的东西
- 10、组合总和 III(216、Medium)
-
- 1)题目要求
- 2)我的解法
- 3)其他解法
- 4)自己的优化代码
- 5)学到的东西
- 11、子集(78、Medium)
-
- 1)题目要求
- 2)我的解法
- 3)其他解法
- 4)自己的优化代码
- 5)学到的东西
- 12、子集 II(90、Medium)
-
- 1)题目要求
- 2)我的解法
- 3)其他解法
- 4)自己的优化代码
- 5)学到的东西
- 13、 分割回文串(131、Medium)
-
- 1)题目要求
- 2)我的解法
- 3)其他解法
- 4)自己的优化代码
- 5)学到的东西
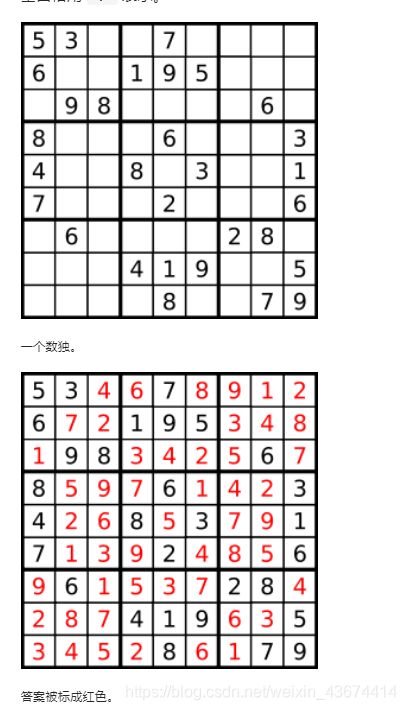
- 14、数独(37、Hard)
-
- 1)题目要求
- 2)我的解法
- 3)其他解法
- 4)自己的优化代码
- 5)学到的东西
- 15、N 皇后(51、Hard)
-
- 1)题目要求
- 2)我的解法
- 3)其他解法
- 4)自己的优化代码
- 5)学到的东西
Backtracking(回溯)
1、电话号码的字母组合(17、Medium)
1)题目要求
2)我的解法
class Solution {
List<String> result;
Map<Integer,String> map;
char[] temp;
public void backtrack(int i,String digits){
if(i>=digits.length())return;
String s=map.get(digits.charAt(i)-'0');
for(int j=0;j<s.length();j++){
temp[i]=s.charAt(j);
if(i==digits.length()-1)result.add(new String(temp));
backtrack(i+1,digits);
}
}
public List<String> letterCombinations(String digits) {
map=new HashMap<>();
result=new ArrayList<>();
temp=new char[digits.length()];
map.put(2,"abc");map.put(3,"def");map.put(4,"ghi");
map.put(5,"jkl");map.put(6,"mno");map.put(7,"pqrs");
map.put(8,"tuv");map.put(9,"wxyz");
backtrack(0,digits);
return result;
}
}
3)其他解法
1、回溯
class Solution {
//一个映射表,第二个位置是"abc“,第三个位置是"def"。。。
//这里也可以用map,用数组可以更节省点内存
String[] letter_map = {" ","*","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
public List<String> letterCombinations(String digits) {
//注意边界条件
if(digits==null || digits.length()==0) {
return new ArrayList<>();
}
iterStr(digits, new StringBuilder(), 0);
return res;
}
//最终输出结果的list
List<String> res = new ArrayList<>();
//递归函数
void iterStr(String str, StringBuilder letter, int index) {
//递归的终止条件,注意这里的终止条件看上去跟动态演示图有些不同,主要是做了点优化
//动态图中是每次截取字符串的一部分,"234",变成"23",再变成"3",最后变成"",这样性能不佳
//而用index记录每次遍历到字符串的位置,这样性能更好
if(index == str.length()) {
res.add(letter.toString());
return;
}
//获取index位置的字符,假设输入的字符是"234"
//第一次递归时index为0所以c=2,第二次index为1所以c=3,第三次c=4
//subString每次都会生成新的字符串,而index则是取当前的一个字符,所以效率更高一点
char c = str.charAt(index);
//map_string的下表是从0开始一直到9, c-'0'就可以取到相对的数组下标位置
//比如c=2时候,2-'0',获取下标为2,letter_map[2]就是"abc"
int pos = c - '0';
String map_string = letter_map[pos];
//遍历字符串,比如第一次得到的是2,页就是遍历"abc"
for(int i=0;i<map_string.length();i++) {
//调用下一层递归,用文字很难描述,请配合动态图理解
letter.append(map_string.charAt(i));
//如果是String类型做拼接效率会比较低
//iterStr(str, letter+map_string.charAt(i), index+1);
iterStr(str, letter, index+1);
letter.deleteCharAt(letter.length()-1);
}
}
}
2、
class Solution {
public List<String> letterCombinations(String digits) {
if(digits==null || digits.length()==0) {
return new ArrayList<String>();
}
//一个映射表,第二个位置是"abc“,第三个位置是"def"。。。
//这里也可以用map,用数组可以更节省点内存
String[] letter_map = {
" ","*","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"
};
List<String> res = new ArrayList<>();
//先往队列中加入一个空字符
res.add("");
for(int i=0;i<digits.length();i++) {
//由当前遍历到的字符,取字典表中查找对应的字符串
String letters = letter_map[digits.charAt(i)-'0'];
int size = res.size();
//计算出队列长度后,将队列中的每个元素挨个拿出来
for(int j=0;j<size;j++) {
//每次都从队列中拿出第一个元素
String tmp = res.remove(0);
//然后跟"def"这样的字符串拼接,并再次放到队列中
for(int k=0;k<letters.length();k++) {
res.add(tmp+letters.charAt(k));
}
}
}
return res;
}
}
作者:wang_ni_ma
链接: link
来源:力扣(LeetCode)
4)自己的优化代码
class Solution {
List<String> result;
Map<Integer,String> map;
char[] temp;
public void backtrack(int i,String digits){
if(i>=digits.length())return;
String s=map.get(digits.charAt(i)-'0');
for(int j=0;j<s.length();j++){
temp[i]=s.charAt(j);
if(i==digits.length()-1)result.add(new String(temp));
backtrack(i+1,digits);
}
}
public List<String> letterCombinations(String digits) {
map=new HashMap<>();
result=new ArrayList<>();
temp=new char[digits.length()];
map.put(2,"abc");map.put(3,"def");map.put(4,"ghi");
map.put(5,"jkl");map.put(6,"mno");map.put(7,"pqrs");
map.put(8,"tuv");map.put(9,"wxyz");
backtrack(0,digits);
return result;
}
}
5)学到的东西
当题目中出现 “所有组合” 等类似字眼时,我们第一感觉就要想到用回溯。
StringBuilder的API:append(), deleteCharAt()
2、 复原IP地址(93、Medium)
1)题目要求
给定一个只包含数字的字符串,复原它并返回所有可能的 IP 地址格式。
有效的 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 ‘.’ 分隔。
例如:“0.1.2.201” 和 “192.168.1.1” 是 有效的 IP 地址,但是 “0.011.255.245”、“192.168.1.312” 和 “[email protected]” 是 无效的 IP 地址。
示例 1:
输入:s = “25525511135”
输出:[“255.255.11.135”,“255.255.111.35”]
示例 2:
输入:s = “0000”
输出:[“0.0.0.0”]
示例 3:
输入:s = “1111”
输出:[“1.1.1.1”]
示例 4:
输入:s = “010010”
输出:[“0.10.0.10”,“0.100.1.0”]
示例 5:
输入:s = “101023”
输出:[“1.0.10.23”,“1.0.102.3”,“10.1.0.23”,“10.10.2.3”,“101.0.2.3”]
2)我的解法
class Solution {
List<String> result;
int cur=0;
public void backtrack(int i,int num,StringBuilder letter,String s){//num代表当前是第几个数
double remainLength=s.length()-i;//字符串剩余字符数
double remainNum=4-num+1;//剩余数字个数
if(remainLength/remainNum>3||remainLength/remainNum<1)return;//剩余的数符合要求
for(int j=1;j<=Math.min(3,remainLength);j++){
//1-3个数依次尝试
cur=0;
if(num==4){//最后一个数就不用试了
for(int k=0;k<remainLength;k++){letter.append(s.charAt(i+k));cur=cur*10+(s.charAt(i+k)-'0');}
if(!(cur>255||(remainLength==2&&cur<10)||(remainLength==3&&cur<100)))result.add(letter.toString());
for(int k=0;k<remainLength;k++)letter.deleteCharAt(letter.length()-1);
return ;
}
for(int k=0;k<j;k++){letter.append(s.charAt(i+k));cur=cur*10+(s.charAt(i+k)-'0');}
if(cur>255||(j==2&&cur<10)||(j==3&&cur<100)){//处理数据不合规范的情况(前缀有0或大于255)
for(int k=0;k<j;k++)letter.deleteCharAt(letter.length()-1);
return ;
}
letter.append(".");
backtrack(i+j,num+1,letter,s);
for(int k=0;k<j+1;k++)letter.deleteCharAt(letter.length()-1);
}
}
public List<String> restoreIpAddresses(String s) {
result=new ArrayList<>();
if(s.length()>12||s.length()<4)return result;
backtrack(0,1,new StringBuilder(),s);
return result;
}
}
3)其他解法
public List<String> restoreIpAddresses(String s) {
List<String> ret = new ArrayList<>();
StringBuilder ip = new StringBuilder();
for(int a = 1 ; a < 4 ; ++ a)
for(int b = 1 ; b < 4 ; ++ b)
for(int c = 1 ; c < 4 ; ++ c)
for(int d = 1 ; d < 4 ; ++ d)
{
if(a + b + c + d == s.length() )
{
int n1 = Integer.parseInt(s.substring(0, a));
int n2 = Integer.parseInt(s.substring(a, a+b));
int n3 = Integer.parseInt(s.substring(a+b, a+b+c));
int n4 = Integer.parseInt(s.substring(a+b+c));
if(n1 <= 255 && n2 <= 255 && n3 <= 255 && n4 <= 255)
{
ip.append(n1).append('.').append(n2)
.append('.').append(n3).append('.').append(n4);
if(ip.length() == s.length() + 3) ret.add(ip.toString());
ip.delete(0, ip.length());
}
}
}
return ret;
}
作者:reals
链接:link
来源:力扣(LeetCode)
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
import java.util.List;
public class Solution {
public List<String> restoreIpAddresses(String s) {
int len = s.length();
List<String> res = new ArrayList<>();
if (len > 12 || len < 4) {
return res;
}
Deque<String> path = new ArrayDeque<>(4);
dfs(s, len, 0, 4, path, res);
return res;
}
// 需要一个变量记录剩余多少段还没被分割
private void dfs(String s, int len, int begin, int residue, Deque<String> path, List<String> res) {
if (begin == len) {
if (residue == 0) {
res.add(String.join(".", path));
}
return;
}
for (int i = begin; i < begin + 3; i++) {
if (i >= len) {
break;
}
if (residue * 3 < len - i) {
continue;
}
if (judgeIpSegment(s, begin, i)) {
String currentIpSegment = s.substring(begin, i + 1);
path.addLast(currentIpSegment);
dfs(s, len, i + 1, residue - 1, path, res);
path.removeLast();
}
}
}
private boolean judgeIpSegment(String s, int left, int right) {
int len = right - left + 1;
if (len > 1 && s.charAt(left) == '0') {
return false;
}
int res = 0;
while (left <= right) {
res = res * 10 + s.charAt(left) - '0';
left++;
}
return res >= 0 && res <= 255;
}
}
作者:liweiwei1419
链接:link
来源:力扣(LeetCode)
4)自己的优化代码
class Solution {
List<String> result;
int cur=0;
public void backtrack(int i,int num,StringBuilder letter,String s){//num代表当前是第几个数
double remainLength=s.length()-i;//字符串剩余字符数
double remainNum=4-num+1;//剩余数字个数
if(remainLength/remainNum>3||remainLength/remainNum<1)return;//剩余的数符不合要求
for(int j=1;j<=Math.min(3,remainLength);j++){
//1-3个数依次尝试
cur=0;
if(num==4){//最后一个数就不用试了
for(int k=0;k<remainLength;k++){letter.append(s.charAt(i+k));cur=cur*10+(s.charAt(i+k)-'0');}
if(!(cur>255||(remainLength==2&&cur<10)||(remainLength==3&&cur<100)))result.add(letter.toString());
for(int k=0;k<remainLength;k++)letter.deleteCharAt(letter.length()-1);//细节:一定记得删
return ;
}
for(int k=0;k<j;k++){letter.append(s.charAt(i+k));cur=cur*10+(s.charAt(i+k)-'0');}
if(cur>255||(j==2&&cur<10)||(j==3&&cur<100)){//处理数据不合规范的情况(前缀有0或大于255)
for(int k=0;k<j;k++)letter.deleteCharAt(letter.length()-1);
return ;
}
letter.append(".");
backtrack(i+j,num+1,letter,s);
for(int k=0;k<j+1;k++)letter.deleteCharAt(letter.length()-1);
}
}
public List<String> restoreIpAddresses(String s) {
result=new ArrayList<>();
if(s.length()>12||s.length()<4)return result;
backtrack(0,1,new StringBuilder(),s);
return result;
}
}
5)学到的东西
回溯思想
先画出树,明确递归截至条件(一定一定要先确定好,比如本题中第四个数特殊处理)、什么时候截枝,再写
不管什么情况,在递归结束返回时(即回溯时)一定要记得在把当前结点再次标记为未访问(本题中即把它从letter中删掉)
3、单词搜索(79、Medium)
1)题目要求
给定一个二维网格和一个单词,找出该单词是否存在于网格中。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
示例:
board =
[
[‘A’,‘B’,‘C’,‘E’],
[‘S’,‘F’,‘C’,‘S’],
[‘A’,‘D’,‘E’,‘E’]
]
给定 word = “ABCCED”, 返回 true
给定 word = “SEE”, 返回 true
给定 word = “ABCB”, 返回 false
提示:
board 和 word 中只包含大写和小写英文字母。
1 <= board.length <= 200
1 <= board[i].length <= 200
1 <= word.length <= 10^3
2)我的解法
class Solution {
boolean[][] visit;
public boolean dfs(int i,int j,int num,char[][] board, String word){
if(i<0||i>=board.length||j<0||j>=board[0].length)return false;
if(board[i][j]!=word.charAt(num))return false;
if(visit[i][j])return false;
if(num==word.length()-1)return true;
visit[i][j]=true;
boolean tag=dfs(i-1,j,num+1,board,word)||dfs(i+1,j,num+1,board,word)||dfs(i,j-1,num+1,board,word)||dfs(i,j+1,num+1,board,word);
visit[i][j]=false;
return tag;
}
public boolean exist(char[][] board, String word) {
visit=new boolean[board.length][board[0].length];
for(int i=0;i<board.length;i++){
for(int j=0;j<board[0].length;j++){
if(board[i][j]==word.charAt(0)){
if(dfs(i,j,0,board,word))return true;
}
}
}
return false;
}
}
3)其他解法
class Solution {
public boolean exist(char[][] board, String word) {
int h = board.length, w = board[0].length;
boolean[][] visited = new boolean[h][w];
for (int i = 0; i < h; i++) {
for (int j = 0; j < w; j++) {
boolean flag = check(board, visited, i, j, word, 0);
if (flag) {
return true;
}
}
}
return false;
}
public boolean check(char[][] board, boolean[][] visited, int i, int j, String s, int k) {
if (board[i][j] != s.charAt(k)) {
return false;
} else if (k == s.length() - 1) {
return true;
}
visited[i][j] = true;
int[][] directions = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
boolean result = false;
for (int[] dir : directions) {
int newi = i + dir[0], newj = j + dir[1];
if (newi >= 0 && newi < board.length && newj >= 0 && newj < board[0].length) {
if (!visited[newi][newj]) {
boolean flag = check(board, visited, newi, newj, s, k + 1);
if (flag) {
result = true;
break;
}
}
}
}
visited[i][j] = false;
return result;
}
}
作者:LeetCode-Solution
链接:link
来源:力扣(LeetCode)
4)自己的优化代码
class Solution {
public boolean dfs(int i,int j,int num,char[][] board, String word){
if(i<0||i>=board.length||j<0||j>=board[0].length)return false;
if(board[i][j]!=word.charAt(num))return false;
if(num==word.length()-1)return true;
board[i][j]='0';
boolean tag=dfs(i-1,j,num+1,board,word)||dfs(i+1,j,num+1,board,word)||dfs(i,j-1,num+1,board,word)||dfs(i,j+1,num+1,board,word);
board[i][j]=word.charAt(num);
return tag;
}
public boolean exist(char[][] board, String word) {
for(int i=0;i<board.length;i++){
for(int j=0;j<board[0].length;j++){
if(board[i][j]==word.charAt(0)){
if(dfs(i,j,0,board,word))return true;
}
}
}
return false;
}
}
5)学到的东西
回溯思想
递归返回(回溯)时,一定记得把当前结点重新置为未访问
4、 二叉树的所有路径(257、Easy)
1)题目要求
给定一个二叉树,返回所有从根节点到叶子节点的路径。
说明: 叶子节点是指没有子节点的节点。
示例:
输入:
1
/
2 3
5
输出: [“1->2->5”, “1->3”]
解释: 所有根节点到叶子节点的路径为: 1->2->5, 1->3
2)我的解法
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
List<String> result;
StringBuilder s=new StringBuilder();
public void backtrack(TreeNode root){
if(root==null)return ;
if(root.left==null&&root.right==null){
s.append(root.val);
result.add(s.toString());
for(int i=0;i<getWei(root.val);i++)s.deleteCharAt(s.length()-1);
return;
}
s.append(root.val);
s.append("->");
backtrack(root.left);
for(int i=0;i<getWei(root.val);i++)s.deleteCharAt(s.length()-1);
s.deleteCharAt(s.length()-1);s.deleteCharAt(s.length()-1);
s.append(root.val);
s.append("->");
backtrack(root.right);
for(int i=0;i<getWei(root.val);i++)s.deleteCharAt(s.length()-1);
s.deleteCharAt(s.length()-1);s.deleteCharAt(s.length()-1);
}
public int getWei(int num){
int re=1;
if(num<0)re++;
if(num/10!=0)re++;
if(num/100!=0)re++;
return re;
}
public List<String> binaryTreePaths(TreeNode root) {
result=new ArrayList<>();
backtrack(root);
return result;
}
}
3)其他解法
class Solution {
public List<String> binaryTreePaths(TreeNode root) {
List<String> paths = new ArrayList<String>();
constructPaths(root, "", paths);
return paths;
}
public void constructPaths(TreeNode root, String path, List<String> paths) {
if (root != null) {
StringBuffer pathSB = new StringBuffer(path);
pathSB.append(Integer.toString(root.val));
if (root.left == null && root.right == null) { // 当前节点是叶子节点
paths.add(pathSB.toString()); // 把路径加入到答案中
} else {
pathSB.append("->"); // 当前节点不是叶子节点,继续递归遍历
constructPaths(root.left, pathSB.toString(), paths);
constructPaths(root.right, pathSB.toString(), paths);
}
}
}
}
class Solution {
public List<String> binaryTreePaths(TreeNode root) {
List<String> paths = new ArrayList<String>();
if (root == null) {
return paths;
}
Queue<TreeNode> nodeQueue = new LinkedList<TreeNode>();
Queue<String> pathQueue = new LinkedList<String>();
nodeQueue.offer(root);
pathQueue.offer(Integer.toString(root.val));
while (!nodeQueue.isEmpty()) {
TreeNode node = nodeQueue.poll();
String path = pathQueue.poll();
if (node.left == null && node.right == null) {
paths.add(path);
} else {
if (node.left != null) {
nodeQueue.offer(node.left);
pathQueue.offer(new StringBuffer(path).append("->").append(node.left.val).toString());
}
if (node.right != null) {
nodeQueue.offer(node.right);
pathQueue.offer(new StringBuffer(path).append("->").append(node.right.val).toString());
}
}
}
return paths;
}
}
作者:LeetCode-Solution
链接:link
来源:力扣(LeetCode)
4)自己的优化代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
List<String> result;
public void backtrack(TreeNode root,String path){
if(root==null)return ;
StringBuilder s=new StringBuilder(path);
if(root.left==null&&root.right==null){
s.append(root.val);
result.add(s.toString());
return;
}
s.append(root.val);
s.append("->");
backtrack(root.left,s.toString());
backtrack(root.right,s.toString());
}
public List<String> binaryTreePaths(TreeNode root) {
result=new ArrayList<>();
backtrack(root,"");
return result;
}
}
5)学到的东西
回溯思想
把备忘录作为backpack函数的形参,这样每次回溯时不必更新备忘录(不必把当前结点重新设为未访问)
5、 全排列(46、Medium)
1)题目要求
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
示例:
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
2)我的解法
class Solution {
List<List<Integer>> result;
List<Integer> temp=new ArrayList<>();
public void backpack(List<Integer> list){
if(list.size()==1){
temp.add(list.get(0));
List<Integer> l=new ArrayList<>();
for(int i=0;i<temp.size();i++)l.add(temp.get(i));
result.add(l);
temp.remove(temp.size()-1);
return;
}
for(int i=0;i<list.size();i++){
int tem=list.get(0);
temp.add(tem);
list.remove(0);
backpack(list);
temp.remove(temp.size()-1);
list.add(tem);
}
}
public List<List<Integer>> permute(int[] nums) {
result=new ArrayList<>();
List<Integer> list=new ArrayList<>();
for(int i=0;i<nums.length;i++)list.add(nums[i]);
backpack(list);
return result;
}
}
3)其他解法
class Solution {
public List<List<Integer>> permute(int[] nums) {
List<List<Integer>> res = new ArrayList<List<Integer>>();
List<Integer> output = new ArrayList<Integer>();
for (int num : nums) {
output.add(num);
}
int n = nums.length;
backtrack(n, output, res, 0);
return res;
}
public void backtrack(int n, List<Integer> output, List<List<Integer>> res, int first) {
// 所有数都填完了
if (first == n) {
res.add(new ArrayList<Integer>(output));
}
for (int i = first; i < n; i++) {
// 动态维护数组
Collections.swap(output, first, i);
// 继续递归填下一个数
backtrack(n, output, res, first + 1);
// 撤销操作
Collections.swap(output, first, i);
}
}
}
作者:LeetCode-Solution
链接:link
来源:力扣(LeetCode)
4)自己的优化代码
class Solution {
List<List<Integer>> result;
List<Integer> temp=new ArrayList<>();
public void backpack(List<Integer> list){
if(list.size()==1){
temp.add(list.get(0));
List<Integer> l=new ArrayList<>(temp);
result.add(l);
temp.remove(temp.size()-1);
return;
}
for(int i=0;i<list.size();i++){
int tem=list.get(0);
temp.add(tem);
list.remove(0);
backpack(list);
temp.remove(temp.size()-1);
list.add(tem);
}
}
public List<List<Integer>> permute(int[] nums) {
result=new ArrayList<>();
List<Integer> list=new ArrayList<>();
for(int i=0;i<nums.length;i++)list.add(nums[i]);
backpack(list);
return result;
}
}
5)学到的东西
回溯思想
构造:new ArrayList<>(另一个arraylist)
Collections.swap():参考 java.util.Collections.swap()方法实例
6、全排列 II(47、Medium)
1)题目要求
给定一个可包含重复数字的序列,返回所有不重复的全排列。
示例:
输入: [1,1,2]
输出:
[
[1,1,2],
[1,2,1],
[2,1,1]
]
2)我的解法
class Solution {
List<List<Integer>> result=new ArrayList<>();
List<Integer> temp=new ArrayList<>();
public void backpack(List<Integer> nums){
if(nums.size()==0)return;
if(nums.size()==1){
temp.add(nums.get(0));
result.add(new ArrayList<Integer>(temp));
temp.remove(temp.size()-1);
return;
}
for(int j=0;j<nums.size();j++){
if(j>0&&nums.get(j)==nums.get(j-1))continue;
temp.add(nums.get(j));
nums.remove(j);
backpack(nums);
nums.add(j,temp.get(temp.size()-1));
temp.remove(temp.size()-1);
}
}
public List<List<Integer>> permuteUnique(int[] nums) {
List<Integer> list=new ArrayList<>();
Arrays.sort(nums);
for(int i=0;i<nums.length;i++)list.add(nums[i]);
backpack(list);
return result;
}
}
3)其他解法
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Deque;
import java.util.List;
public class Solution {
public List<List<Integer>> permuteUnique(int[] nums) {
int len = nums.length;
List<List<Integer>> res = new ArrayList<>();
if (len == 0) {
return res;
}
// 排序(升序或者降序都可以),排序是剪枝的前提
Arrays.sort(nums);
boolean[] used = new boolean[len];
// 使用 Deque 是 Java 官方 Stack 类的建议
Deque<Integer> path = new ArrayDeque<>(len);
dfs(nums, len, 0, used, path, res);
return res;
}
private void dfs(int[] nums, int len, int depth, boolean[] used, Deque<Integer> path, List<List<Integer>> res) {
if (depth == len) {
res.add(new ArrayList<>(path));
return;
}
for (int i = 0; i < len; ++i) {
if (used[i]) {
continue;
}
// 剪枝条件:i > 0 是为了保证 nums[i - 1] 有意义
// 写 !used[i - 1] 是因为 nums[i - 1] 在深度优先遍历的过程中刚刚被撤销选择
if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
continue;
}
path.addLast(nums[i]);
used[i] = true;
dfs(nums, len, depth + 1, used, path, res);
// 回溯部分的代码,和 dfs 之前的代码是对称的
used[i] = false;
path.removeLast();
}
}
}
作者:liweiwei1419
链接:link
来源:力扣(LeetCode)
4)自己的优化代码
class Solution {
List<List<Integer>> result=new ArrayList<>();
List<Integer> temp=new ArrayList<>();
public void backpack(List<Integer> nums){
if(nums.size()==0)return;
if(nums.size()==1){
temp.add(nums.get(0));
result.add(new ArrayList<Integer>(temp));
temp.remove(temp.size()-1);
return;
}
for(int j=0;j<nums.size();j++){
if(j>0&&nums.get(j)==nums.get(j-1))continue;
temp.add(nums.get(j));
nums.remove(j);
backpack(nums);
nums.add(j,temp.get(temp.size()-1));
temp.remove(temp.size()-1);
}
}
public List<List<Integer>> permuteUnique(int[] nums) {
List<Integer> list=new ArrayList<>();
Arrays.sort(nums);
for(int i=0;i<nums.length;i++)list.add(nums[i]);
backpack(list);
return result;
}
}
5)学到的东西
先画树再写
分析重复原因,进行剪枝
尽量把int[]换成list,方便增删
7、组合(77、Medium)
1)题目要求
给定两个整数 n 和 k,返回 1 … n 中所有可能的 k 个数的组合。
示例:
输入: n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
2)我的解法
class Solution {
List<Integer> temp=new ArrayList<>();
int deep;
int N;
List<List<Integer>> result=new ArrayList<>();
public void backpack(int start,int ceng){
if(start>N)return;
if(ceng==deep){
for(int i=start;i<=N;i++){
temp.add(i);
result.add(new ArrayList<>(temp));
temp.remove(temp.size()-1);
}
return;
}
for(int i=start;i<=N;i++){
temp.add(i);
backpack(i+1,ceng+1);
temp.remove(temp.size()-1);
}
}
public List<List<Integer>> combine(int n, int k) {
deep=k;
N=n;
backpack(1,1);
return result;
}
}
3)其他解法
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
import java.util.List;
public class Solution {
public List<List<Integer>> combine(int n, int k) {
List<List<Integer>> res = new ArrayList<>();
if (k <= 0 || n < k) {
return res;
}
Deque<Integer> path = new ArrayDeque<>();
dfs(n, k, 1, path, res);
return res;
}
private void dfs(int n, int k, int index, Deque<Integer> path, List<List<Integer>> res) {
if (path.size() == k) {
res.add(new ArrayList<>(path));
return;
}
// 只有这里 i <= n - (k - path.size()) + 1 与参考代码 1 不同
for (int i = index; i <= n - (k - path.size()) + 1; i++) {
path.addLast(i);
dfs(n, k, i + 1, path, res);
path.removeLast();
}
}
}
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
import java.util.List;
public class Solution {
public List<List<Integer>> combine(int n, int k) {
List<List<Integer>> res = new ArrayList<>();
if (k <= 0 || n < k) {
return res;
}
// 为了防止底层动态数组扩容,初始化的时候传入最大长度
Deque<Integer> path = new ArrayDeque<>(k);
dfs(1, n, k, path, res);
return res;
}
private void dfs(int begin, int n, int k, Deque<Integer> path, List<List<Integer>> res) {
if (k == 0) {
res.add(new ArrayList<>(path));
return;
}
// 基础版本的递归终止条件:if (begin == n + 1) {
if (begin > n - k + 1) {
return;
}
// 不选当前考虑的数 begin,直接递归到下一层
dfs(begin + 1, n, k, path, res);
// 不选当前考虑的数 begin,递归到下一层的时候 k - 1,这里 k 表示还需要选多少个数
path.addLast(begin);
dfs(begin + 1, n, k - 1, path, res);
// 深度优先遍历有回头的过程,因此需要撤销选择
path.removeLast();
}
}
作者:liweiwei1419
链接: link
来源:力扣(LeetCode)
4)自己的优化代码
class Solution {
List<Integer> temp=new ArrayList<>();
int deep;
int N;
List<List<Integer>> result=new ArrayList<>();
public void backpack(int start,int ceng){
if(start>N)return;
if(ceng==deep){
for(int i=start;i<=N;i++){
temp.add(i);
result.add(new ArrayList<>(temp));
temp.remove(temp.size()-1);
}
return;
}
for(int i=start;i<=N-deep+ceng;i++){
temp.add(i);
backpack(i+1,ceng+1);
temp.remove(temp.size()-1);
}
}
public List<List<Integer>> combine(int n, int k) {
deep=k;
N=n;
backpack(1,1);
return result;
}
}
5)学到的东西
剪枝除了可以用来去重,还可以提高效率,比如本题去重后还可以继续剪枝
8、组合总和(39、Medium)
1)题目要求
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
所有数字(包括 target)都是正整数。
解集不能包含重复的组合。
示例 1:
输入:candidates = [2,3,6,7], target = 7,
所求解集为:
[
[7],
[2,2,3]
]
示例 2:
输入:candidates = [2,3,5], target = 8,
所求解集为:
[
[2,2,2,2],
[2,3,3],
[3,5]
]
提示:
1 <= candidates.length <= 30
1 <= candidates[i] <= 200
candidate 中的每个元素都是独一无二的。
1 <= target <= 500
2)我的解法
class Solution {
List<List<Integer>> result;
List<Integer> temp=new ArrayList<>();
public void backpack(int[] candidates, int target){
if(target==0){
result.add(new ArrayList<Integer>(temp));
return;
}
if(target<0)return;
for(int i=0;i<candidates.length;i++){
temp.add(candidates[i]);
backpack(candidates,target-candidates[i]);
temp.remove(temp.size()-1);
}
}
public void quchong(){
for(int i=0;i<result.size();i++){
for(int j=i+1;j<result.size();j++){
if(result.get(i).size()==result.get(j).size()){
result.get(i).sort((o1,o2)->o1-o2);
result.get(j).sort((o1,o2)->o1-o2);
if(result.get(i).equals(result.get(j))){
result.remove(j);
j--;
}
}
}
}
}
public List<List<Integer>> combinationSum(int[] candidates, int target) {
result=new ArrayList<>();
backpack(candidates,target);
quchong();
return result;
}
}
优化(排序后剪枝)
class Solution {
List<List<Integer>> result;
List<Integer> temp=new ArrayList<>();
public void backpack(int[] candidates,int start, int target){
if(target==0){
result.add(new ArrayList<Integer>(temp));
return;
}
if(target<0)return;
for(int i=start;i<candidates.length;i++){
temp.add(candidates[i]);
backpack(candidates,i,target-candidates[i]);
//之后不得访问当前结点之前的元素,但可以继续访问当前结点
temp.remove(temp.size()-1);
}
}
public List<List<Integer>> combinationSum(int[] candidates, int target) {
result=new ArrayList<>();
Arrays.sort(candidates);
backpack(candidates,0,target);
return result;
}
}
3)其他解法
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
import java.util.List;
public class Solution {
public List<List<Integer>> combinationSum(int[] candidates, int target) {
int len = candidates.length;
List<List<Integer>> res = new ArrayList<>();
if (len == 0) {
return res;
}
Deque<Integer> path = new ArrayDeque<>();
dfs(candidates, 0, len, target, path, res);
return res;
}
/**
* @param candidates 候选数组
* @param begin 搜索起点
* @param len 冗余变量,是 candidates 里的属性,可以不传
* @param target 每减去一个元素,目标值变小
* @param path 从根结点到叶子结点的路径,是一个栈
* @param res 结果集列表
*/
private void dfs(int[] candidates, int begin, int len, int target, Deque<Integer> path, List<List<Integer>> res) {
// target 为负数和 0 的时候不再产生新的孩子结点
if (target < 0) {
return;
}
if (target == 0) {
res.add(new ArrayList<>(path));
return;
}
// 重点理解这里从 begin 开始搜索的语意
for (int i = begin; i < len; i++) {
path.addLast(candidates[i]);
// 注意:由于每一个元素可以重复使用,下一轮搜索的起点依然是 i,这里非常容易弄错
dfs(candidates, i, len, target - candidates[i], path, res);
// 状态重置
path.removeLast();
}
}
}
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Deque;
import java.util.List;
public class Solution {
public List<List<Integer>> combinationSum(int[] candidates, int target) {
int len = candidates.length;
List<List<Integer>> res = new ArrayList<>();
if (len == 0) {
return res;
}
// 排序是剪枝的前提
Arrays.sort(candidates);
Deque<Integer> path = new ArrayDeque<>();
dfs(candidates, 0, len, target, path, res);
return res;
}
private void dfs(int[] candidates, int begin, int len, int target, Deque<Integer> path, List<List<Integer>> res) {
// 由于进入更深层的时候,小于 0 的部分被剪枝,因此递归终止条件值只判断等于 0 的情况
if (target == 0) {
res.add(new ArrayList<>(path));
return;
}
for (int i = begin; i < len; i++) {
// 重点理解这里剪枝,前提是候选数组已经有序,
if (target - candidates[i] < 0) {
break;
}
path.addLast(candidates[i]);
dfs(candidates, i, len, target - candidates[i], path, res);
path.removeLast();
}
}
}
作者:liweiwei1419
链接:link
来源:力扣(LeetCode)
4)自己的优化代码
class Solution {
List<List<Integer>> result;
List<Integer> temp=new ArrayList<>();
public void backpack(int[] candidates,int start, int target){
if(target==0){
result.add(new ArrayList<Integer>(temp));
return;
}
if(target<0)return;
for(int i=start;i<candidates.length;i++){//排序,并且之后不得访问当前结点之前的元素,但可以继续访问当前结点
temp.add(candidates[i]);
backpack(candidates,i,target-candidates[i]);
temp.remove(temp.size()-1);
}
}
public List<List<Integer>> combinationSum(int[] candidates, int target) {
result=new ArrayList<>();
Arrays.sort(candidates);
backpack(candidates,0,target);
return result;
}
}
5)学到的东西
回溯思想
尽量不在dfs之后去重,而是在搜索过程中剪枝
思想:指定下一层从哪个结点开始
9、组合总和 II(40、Medium)
1)题目要求
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。
说明:
所有数字(包括目标数)都是正整数。
解集不能包含重复的组合。
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
[1, 7],
[1, 2, 5],
[2, 6],
[1, 1, 6]
]
示例 2:
输入: candidates = [2,5,2,1,2], target = 5,
所求解集为:
[
[1,2,2],
[5]
]
2)我的解法
class Solution {
List<List<Integer>> result=new ArrayList<>();
List<Integer> temp=new ArrayList<>();
public void backpack(int[] candidates,int start, int target){
if(target==0){
result.add(new ArrayList<Integer>(temp));
return;
}
if(target<0)return;
for(int i=start;i<candidates.length;i++){
if(i>start&&candidates[i]==candidates[i-1])continue;
temp.add(candidates[i]);
backpack(candidates,i+1,target-candidates[i]);
temp.remove(temp.size()-1);
}
}
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
Arrays.sort(candidates);
backpack(candidates,0,target);
return result;
}
}
3)其他解法
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Deque;
import java.util.List;
public class Solution {
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
int len = candidates.length;
List<List<Integer>> res = new ArrayList<>();
if (len == 0) {
return res;
}
// 关键步骤
Arrays.sort(candidates);
Deque<Integer> path = new ArrayDeque<>(len);
dfs(candidates, len, 0, target, path, res);
return res;
}
/**
* @param candidates 候选数组
* @param len 冗余变量
* @param begin 从候选数组的 begin 位置开始搜索
* @param target 表示剩余,这个值一开始等于 target,基于题目中说明的"所有数字(包括目标数)都是正整数"这个条件
* @param path 从根结点到叶子结点的路径
* @param res
*/
private void dfs(int[] candidates, int len, int begin, int target, Deque<Integer> path, List<List<Integer>> res) {
if (target == 0) {
res.add(new ArrayList<>(path));
return;
}
for (int i = begin; i < len; i++) {
// 大剪枝:减去 candidates[i] 小于 0,减去后面的 candidates[i + 1]、candidates[i + 2] 肯定也小于 0,因此用 break
if (target - candidates[i] < 0) {
break;
}
// 小剪枝:同一层相同数值的结点,从第 2 个开始,候选数更少,结果一定发生重复,因此跳过,用 continue
if (i > begin && candidates[i] == candidates[i - 1]) {
continue;
}
path.addLast(candidates[i]);
// 调试语句 ①
// System.out.println("递归之前 => " + path + ",剩余 = " + (target - candidates[i]));
// 因为元素不可以重复使用,这里递归传递下去的是 i + 1 而不是 i
dfs(candidates, len, i + 1, target - candidates[i], path, res);
path.removeLast();
// 调试语句 ②
// System.out.println("递归之后 => " + path + ",剩余 = " + (target - candidates[i]));
}
}
public static void main(String[] args) {
int[] candidates = new int[]{10, 1, 2, 7, 6, 1, 5};
int target = 8;
Solution solution = new Solution();
List<List<Integer>> res = solution.combinationSum2(candidates, target);
System.out.println("输出 => " + res);
}
}
作者:liweiwei1419
链接: link
来源:力扣(LeetCode)
4)自己的优化代码
class Solution {
List<List<Integer>> result=new ArrayList<>();
List<Integer> temp=new ArrayList<>();
public void backpack(int[] candidates,int start, int target){
if(target==0){
result.add(new ArrayList<Integer>(temp));
return;
}
if(target<0)return;
for(int i=start;i<candidates.length;i++){
if(i>start&&candidates[i]==candidates[i-1])continue;
temp.add(candidates[i]);
backpack(candidates,i+1,target-candidates[i]);
temp.remove(temp.size()-1);
}
}
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
Arrays.sort(candidates);
backpack(candidates,0,target);
return result;
}
}
5)学到的东西
回溯思想
在去重时,分析重复原因,并据此在搜索过程中进行剪枝
10、组合总和 III(216、Medium)
1)题目要求
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。
说明:
所有数字都是正整数。
解集不能包含重复的组合。
示例 1:
输入: k = 3, n = 7
输出: [[1,2,4]]
示例 2:
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
2)我的解法
class Solution {
List<List<Integer>> result=new ArrayList<>();
int N;//目标值
int deep;//最大深度
int max;//每层最大结点
int remainCeng;//剩余层
List<Integer> temp=new ArrayList<>();
public void backpack(int start,int ceng,int target){
//start为本层开始结点,ceng为当前层数,target为目标数
if(ceng==deep){//最后一层不必遍历,直接找
if(target>9||target<start)return;
temp.add(target);
result.add(new ArrayList<Integer>(temp));
temp.remove(temp.size()-1);
return;
}
remainCeng=deep-ceng+1;
max=(target-((remainCeng-1)*(1+remainCeng-1)/2))/remainCeng;//每层不用把1-9都遍历一遍,找出最大结点,遍历到最大结点就停即可
//3*x+3<=7 x<=1
for(int i=start;i<=9&&i<=max;i++){
temp.add(i);
backpack(i+1,ceng+1,target-i);
temp.remove(temp.size()-1);
}
}
public List<List<Integer>> combinationSum3(int k, int n) {
N=n;
deep=k;
backpack(1,1,n);
return result;
}
}
3)其他解法
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
import java.util.List;
public class Solution {
public List<List<Integer>> combinationSum3(int k, int n) {
List<List<Integer>> res = new ArrayList<>();
// 一开始做一些特殊判断
if (k <= 0 || n <= 0 || k >= n) {
return res;
}
// 寻找 n 的上限:[9, 8, ... , (9 - k + 1)],它们的和为 (19 - k) * k / 2
// 比上限还大,就不用搜索了:
if (n > (19 - k) * k / 2) {
return res;
}
// 根据官方对 Stack 的使用建议,这里将 Deque 对象当做 stack 使用
// 注意只使用关于栈的接口
Deque<Integer> path = new ArrayDeque<>();
dfs(k, n, 1, path, res);
return res;
}
/**
* @param k 剩下要找 k 个数
* @param residue 剩余多少
* @param start 下一轮搜索的起始元素是多少
* @param path 深度优先遍历的路径参数(状态变量)
* @param res 保存结果集的列表
*/
private void dfs(int k, int residue, int start, Deque<Integer> path, List<List<Integer>> res) {
// 剪枝:[start, 9] 这个区间里的数都不够 k 个,不用继续往下搜索
if (10 - start < k) {
return;
}
if (k == 0) {
if (residue == 0) {
res.add(new ArrayList<>(path));
return;
}
}
// 枚举起点值 [..., 7, 8, 9]
// 找 3 个数,起点最多到 7
// 找 2 个数,起点最多到 8
// 规律是,起点上界 + k = 10,故起点上界 = 10 - k
for (int i = start; i <= 10 - k; i++) {
// if ((2 * i + k - 1) * k / 2 > residue) {
// break;
// }
// 剪枝
if (residue - i < 0) {
break;
}
path.addLast(i);
dfs(k - 1, residue - i, i + 1, path, res);
path.removeLast();
}
}
}
作者:liweiwei1419
链接:link
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
4)自己的优化代码
class Solution {
List<List<Integer>> result=new ArrayList<>();
int N;//目标值
int deep;//最大深度
int max;//每层最大结点
int remainCeng;//剩余层
List<Integer> temp=new ArrayList<>();
public void backpack(int start,int ceng,int target){
//start为本层开始结点,ceng为当前层数,target为目标数
if(ceng==deep){//最后一层不必遍历,直接找
if(target>9||target<start)return;
temp.add(target);
result.add(new ArrayList<Integer>(temp));
temp.remove(temp.size()-1);
return;
}
remainCeng=deep-ceng+1;
max=(target-((remainCeng-1)*(1+remainCeng-1)/2))/remainCeng;//每层不用把1-9都遍历一遍,找出最大结点,遍历到最大结点就停即可
//3*x+3<=7 x<=1
for(int i=start;i<=9&&i<=max;i++){
temp.add(i);
backpack(i+1,ceng+1,target-i);
temp.remove(temp.size()-1);
}
}
public List<List<Integer>> combinationSum3(int k, int n) {
N=n;
deep=k;
backpack(1,1,n);
return result;
}
}
5)学到的东西
画树,把能剪的枝条全剪掉
11、子集(78、Medium)
1)题目要求
给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例:
输入: nums = [1,2,3]
输出:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]
2)我的解法
class Solution {
List<List<Integer>> result=new ArrayList<>();
List<Integer> temp=new ArrayList<>();
public void backpack(int start,int[] nums){
for(int i=start;i<nums.length;i++){
temp.add(nums[i]);
result.add(new ArrayList<Integer>(temp));
backpack(i+1,nums);
temp.remove(temp.size()-1);
}
}
public List<List<Integer>> subsets(int[] nums) {
result.add(new ArrayList<Integer>());
backpack(0,nums);
return result;
}
}
3)其他解法
class Solution {
List<Integer> t = new ArrayList<Integer>();
List<List<Integer>> ans = new ArrayList<List<Integer>>();
public List<List<Integer>> subsets(int[] nums) {
int n = nums.length;
for (int mask = 0; mask < (1 << n); ++mask) {
t.clear();
for (int i = 0; i < n; ++i) {
if ((mask & (1 << i)) != 0) {
t.add(nums[i]);
}
}
ans.add(new ArrayList<Integer>(t));
}
return ans;
}
}
2、回溯
class Solution {
List<Integer> t = new ArrayList<Integer>();
List<List<Integer>> ans = new ArrayList<List<Integer>>();
public List<List<Integer>> subsets(int[] nums) {
dfs(0, nums);
return ans;
}
public void dfs(int cur, int[] nums) {
if (cur == nums.length) {
ans.add(new ArrayList<Integer>(t));
return;
}
t.add(nums[cur]);
dfs(cur + 1, nums);
t.remove(t.size() - 1);
dfs(cur + 1, nums);
}
}
作者:LeetCode-Solution
链接:link
来源:力扣(LeetCode)
4)自己的优化代码
class Solution {
List<List<Integer>> result=new ArrayList<>();
List<Integer> temp=new ArrayList<>();
public void backpack(int start,int[] nums){
for(int i=start;i<nums.length;i++){
temp.add(nums[i]);
result.add(new ArrayList<Integer>(temp));
backpack(i+1,nums);
temp.remove(temp.size()-1);
}
}
public List<List<Integer>> subsets(int[] nums) {
result.add(new ArrayList<Integer>());
backpack(0,nums);
return result;
}
}
5)学到的东西
不要钻牛角尖过于追求效率高
先画出最普通的回溯树,再在此基础上剪去不必要的枝条即可,不要想一些骚套路
以往都是回溯到最后一层记录,本题为在回溯过程中记录
12、子集 II(90、Medium)
1)题目要求
给定一个可能包含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例:
输入: [1,2,2]
输出:
[
[2],
[1],
[1,2,2],
[2,2],
[1,2],
[]
]
2)我的解法
class Solution {
List<List<Integer>> result=new ArrayList<>();
List<Integer> temp=new ArrayList<>();
public void backpack(int start,int[] nums){
for(int i=start;i<nums.length;i++){
if(i>start&&nums[i]==nums[i-1])continue;
temp.add(nums[i]);
result.add(new ArrayList<Integer>(temp));
backpack(i+1,nums);
temp.remove(temp.size()-1);
}
}
public List<List<Integer>> subsetsWithDup(int[] nums) {
result.add(new ArrayList<Integer>());
Arrays.sort(nums);
backpack(0,nums);
return result;
}
}
3)其他解法
public List<List<Integer>> subsetsWithDup(int[] nums) {
List<List<Integer>> ans = new ArrayList<>();
Arrays.sort(nums); //排序
getAns(nums, 0, new ArrayList<>(), ans);
return ans;
}
private void getAns(int[] nums, int start, ArrayList<Integer> temp, List<List<Integer>> ans) {
ans.add(new ArrayList<>(temp));
for (int i = start; i < nums.length; i++) {
//和上个数字相等就跳过
if (i > start && nums[i] == nums[i - 1]) {
continue;
}
temp.add(nums[i]);
getAns(nums, i + 1, temp, ans);
temp.remove(temp.size() - 1);
}
}
作者:windliang
链接:link
来源:力扣(LeetCode)
4)自己的优化代码
class Solution {
List<List<Integer>> result=new ArrayList<>();
List<Integer> temp=new ArrayList<>();
public void backpack(int start,int[] nums){
for(int i=start;i<nums.length;i++){
if(i>start&&nums[i]==nums[i-1])continue;
temp.add(nums[i]);
result.add(new ArrayList<Integer>(temp));
backpack(i+1,nums);
temp.remove(temp.size()-1);
}
}
public List<List<Integer>> subsetsWithDup(int[] nums) {
result.add(new ArrayList<Integer>());
Arrays.sort(nums);
backpack(0,nums);
return result;
}
}
5)学到的东西
回溯、剪枝
位操作
13、 分割回文串(131、Medium)
1)题目要求
给定一个字符串 s,将 s 分割成一些子串,使每个子串都是回文串。
返回 s 所有可能的分割方案。
示例:
输入: “aab”
输出:
[
[“aa”,“b”],
[“a”,“a”,“b”]
]
2)我的解法
按照截取位置,比如aab,其截取位置有两个,即a 1 a 2 b,然后此题就变成了找出[1,2]的所有子集,找出来之后再进行剪枝,剪去不是回文的即可
class Solution {
List<List<String>> result=new ArrayList<>();
List<String> temp=new ArrayList<>();
public void backpack(String s){
for(int i=0;i<s.length()-1;i++){
if(!isHuiWen(s.substring(0,i+1)))continue;
temp.add(s.substring(0,i+1));
if(isHuiWen(s.substring(i+1))){
temp.add(s.substring(i+1));
result.add(new ArrayList<String>(temp));
temp.remove(temp.size()-1);
}
backpack(s.substring(i+1));
temp.remove(temp.size()-1);
}
}
public boolean isHuiWen(String s){
for(int i=0;2*i+1<=s.length();i++){
if(s.charAt(i)!=s.charAt(s.length()-i-1))return false;
}
return true;
}
public List<List<String>> partition(String s) {
backpack(s);
if(isHuiWen(s)){temp.add(s);result.add(new ArrayList<>(temp));}//s本身单独判断
return result;
}
}
3)其他解法
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
import java.util.List;
public class Solution {
public List<List<String>> partition(String s) {
int len = s.length();
List<List<String>> res = new ArrayList<>();
if (len == 0) {
return res;
}
// Stack 这个类 Java 的文档里推荐写成 Deque stack = new ArrayDeque();
// 注意:只使用 stack 相关的接口
Deque<String> stack = new ArrayDeque<>();
backtracking(s, 0, len, stack, res);
return res;
}
/**
* @param s
* @param start 起始字符的索引
* @param len 字符串 s 的长度,可以设置为全局变量
* @param path 记录从根结点到叶子结点的路径
* @param res 记录所有的结果
*/
private void backtracking(String s, int start, int len, Deque<String> path, List<List<String>> res) {
if (start == len) {
res.add(new ArrayList<>(path));
return;
}
for (int i = start; i < len; i++) {
// 因为截取字符串是消耗性能的,因此,采用传子串索引的方式判断一个子串是否是回文子串
// 不是的话,剪枝
if (!checkPalindrome(s, start, i)) {
continue;
}
path.addLast(s.substring(start, i + 1));
backtracking(s, i + 1, len, path, res);
path.removeLast();
}
}
/**
* 这一步的时间复杂度是 O(N),因此,可以采用动态规划先把回文子串的结果记录在一个表格里
*
* @param str
* @param left 子串的左边界,可以取到
* @param right 子串的右边界,可以取到
* @return
*/
private boolean checkPalindrome(String str, int left, int right) {
// 严格小于即可
while (left < right) {
if (str.charAt(left) != str.charAt(right)) {
return false;
}
left++;
right--;
}
return true;
}
}
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
import java.util.List;
import java.util.Stack;
public class Solution {
public List<List<String>> partition(String s) {
int len = s.length();
List<List<String>> res = new ArrayList<>();
if (len == 0) {
return res;
}
// 预处理
// 状态:dp[i][j] 表示 s[i][j] 是否是回文
boolean[][] dp = new boolean[len][len];
// 状态转移方程:在 s[i] == s[j] 的时候,dp[i][j] 参考 dp[i + 1][j - 1]
for (int right = 0; right < len; right++) {
// 注意:left <= right 取等号表示 1 个字符的时候也需要判断
for (int left = 0; left <= right; left++) {
if (s.charAt(left) == s.charAt(right) && (right - left <= 2 || dp[left + 1][right - 1])) {
dp[left][right] = true;
}
}
}
Deque<String> stack = new ArrayDeque<>();
backtracking(s, 0, len, dp, stack, res);
return res;
}
private void backtracking(String s,
int start,
int len,
boolean[][] dp,
Deque<String> path,
List<List<String>> res) {
if (start == len) {
res.add(new ArrayList<>(path));
return;
}
for (int i = start; i < len; i++) {
// 剪枝
if (!dp[start][i]) {
continue;
}
path.addLast(s.substring(start, i + 1));
backtracking(s, i + 1, len, dp, path, res);
path.removeLast();
}
}
}
作者:liweiwei1419
链接:link
来源:力扣(LeetCode)
4)自己的优化代码
class Solution {
List<List<String>> result=new ArrayList<>();
List<String> temp=new ArrayList<>();
public void backpack(String s){
for(int i=0;i<s.length()-1;i++){
if(!isHuiWen(s.substring(0,i+1)))continue;
temp.add(s.substring(0,i+1));
if(isHuiWen(s.substring(i+1))){
temp.add(s.substring(i+1));
result.add(new ArrayList<String>(temp));
temp.remove(temp.size()-1);
}
backpack(s.substring(i+1));
temp.remove(temp.size()-1);
}
}
public boolean isHuiWen(String s){
for(int i=0;2*i+1<=s.length();i++){
if(s.charAt(i)!=s.charAt(s.length()-i-1))return false;
}
return true;
}
public List<List<String>> partition(String s) {
backpack(s);
if(isHuiWen(s)){temp.add(s);result.add(new ArrayList<>(temp));}//s本身单独判断
return result;
}
}
5)学到的东西
画树、剪枝
利用动态规划判断回文
14、数独(37、Hard)
1)题目要求
编写一个程序,通过填充空格来解决数独问题。
一个数独的解法需遵循如下规则:
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
空白格用 ‘.’ 表示。
提示:
给定的数独序列只包含数字 1-9 和字符 ‘.’ 。
你可以假设给定的数独只有唯一解。
给定数独永远是 9x9 形式的。
2)我的解法
1、严重超时,但能得出正确结果
class Solution {
int[][][] visited =new int[9][9][9];
int nexti=0,nextj=0;
public boolean backpack(int i,int j,char[][] board){
if(i>=9)return true;
if(board[i][j]!='.'){
if(visited[i][j][board[i][j]-'1']>0)return false;
makeVisited(i,j,board);
if(j<8){nexti=i;nextj=j+1;}
if(j==8){nexti=i+1;nextj=0;}
if(backpack(nexti,nextj,board))return true;
makeUnVisited(i,j,board);
return false;
}
else{
for(int k=0;k<9;k++){
if(visited[i][j][k]>0)continue;
board[i][j]=(char)(k+'1');
makeVisited(i,j,board);
System.out.println(i+" "+j+" "+board[i][j]);
if(j<8){nexti=i;nextj=j+1;}
if(j==8){nexti=i+1;nextj=0;}
if(backpack(nexti,nextj,board))return true;
makeUnVisited(i,j,board);
board[i][j]='.';
}
return false;
}
}
public void makeVisited(int i,int j,char[][] board){
for(int k=0;k<9;k++){
visited[i][k][board[i][j]-'1']++;
visited[k][j][board[i][j]-'1']++;
}
int x=i/3,y=j/3;
x*=3;y*=3;
for(int p=x;p<x+3;p++){
for(int q=y;q<y+3;q++){
visited[p][q][board[i][j]-'1']++;
}
}
}
public void makeUnVisited(int i,int j,char[][] board){
for(int k=0;k<9;k++){
visited[i][k][board[i][j]-'1']--;
visited[k][j][board[i][j]-'1']--;
}
int x=i/3,y=j/3;
x*=3;y*=3;
for(int p=x;p<x+3;p++){
for(int q=y;q<y+3;q++){
visited[p][q][board[i][j]-'1']--;
}
}
}
public void solveSudoku(char[][] board) {
backpack(0,0,board);
}
}
2、改进备忘录,用空间换时间:还是超时。。.。
class Solution {
boolean[][] Cvisited =new boolean[9][9];//行
boolean[][] Rvisited =new boolean[9][9];//列
boolean[][][] CRvisited =new boolean[3][3][9];//3*3
int nexti=0,nextj=0;
public boolean backpack(int i,int j,char[][] board){
if(i>=9)return true;
if(board[i][j]!='.'){
if(IsVisited(i,j,board[i][j]-'1'))return false;
makeVisited(i,j,board);
if(j<8){nexti=i;nextj=j+1;}
if(j==8){nexti=i+1;nextj=0;}
if(backpack(nexti,nextj,board))return true;
makeUnVisited(i,j,board);
return false;
}
else{
for(int k=0;k<9;k++){
if(IsVisited(i,j,k))continue;
board[i][j]=(char)(k+'1');
makeVisited(i,j,board);
if(j<8){nexti=i;nextj=j+1;}
if(j==8){nexti=i+1;nextj=0;}
if(backpack(nexti,nextj,board))return true;
makeUnVisited(i,j,board);
board[i][j]='.';
}
return false;
}
}
public boolean IsVisited(int i,int j,int k){
return Cvisited[i][k]||Rvisited[j][k]||CRvisited[i/3][j/3][k];
}
public void makeVisited(int i,int j,char[][] board){
Cvisited[i][board[i][j]-'1']=true;
Rvisited[j][board[i][j]-'1']=true;
CRvisited[i/3][j/3][board[i][j]-'1']=true;
}
public void makeUnVisited(int i,int j,char[][] board){
Cvisited[i][board[i][j]-'1']=false;
Rvisited[j][board[i][j]-'1']=false;
CRvisited[i/3][j/3][board[i][j]-'1']=false;
}
public void solveSudoku(char[][] board) {
backpack(0,0,board);
}
}
3、再次改进,先进行初始化:通过
class Solution {
boolean[][] Cvisited =new boolean[9][9];//行
boolean[][] Rvisited =new boolean[9][9];//列
boolean[][][] CRvisited =new boolean[3][3][9];//3*3
int nexti=0,nextj=0;
public boolean backpack(int i,int j,char[][] board){
if(i>=9)return true;
if(board[i][j]!='.'){
if(j<8){nexti=i;nextj=j+1;}
if(j==8){nexti=i+1;nextj=0;}
if(backpack(nexti,nextj,board))return true;
return false;
}
else{
for(int k=0;k<9;k++){
if(IsVisited(i,j,k))continue;
board[i][j]=(char)(k+'1');
makeVisited(i,j,board);
if(j<8){nexti=i;nextj=j+1;}
if(j==8){nexti=i+1;nextj=0;}
if(backpack(nexti,nextj,board))return true;
makeUnVisited(i,j,board);
board[i][j]='.';
}
return false;
}
}
public boolean IsVisited(int i,int j,int k){
return Cvisited[i][k]||Rvisited[j][k]||CRvisited[i/3][j/3][k];
}
public void makeVisited(int i,int j,char[][] board){
Cvisited[i][board[i][j]-'1']=true;
Rvisited[j][board[i][j]-'1']=true;
CRvisited[i/3][j/3][board[i][j]-'1']=true;
}
public void makeUnVisited(int i,int j,char[][] board){
Cvisited[i][board[i][j]-'1']=false;
Rvisited[j][board[i][j]-'1']=false;
CRvisited[i/3][j/3][board[i][j]-'1']=false;
}
public void solveSudoku(char[][] board) {
for(int i=0;i<9;i++){
for(int j=0;j<9;j++){
if(board[i][j]!='.'){
makeVisited(i,j,board);
}
}
}
backpack(0,0,board);
}
}
3)其他解法
解数独思路:
类似人的思考方式去尝试,行,列,还有 3*3 的方格内数字是 1~9 不能重复。
我们尝试填充,如果发现重复了,那么擦除重新进行新一轮的尝试,直到把整个数组填充完成。
算法步骤:
数独首先行,列,还有 3*3 的方格内数字是 1~9 不能重复。
声明布尔数组,表明行列中某个数字是否被使用了, 被用过视为 true,没用过为 false。
初始化布尔数组,表明哪些数字已经被使用过了。
尝试去填充数组,只要行,列, 还有 3*3 的方格内 出现已经被使用过的数字,我们就不填充,否则尝试填充。
如果填充失败,那么我们需要回溯。将原来尝试填充的地方改回来。
class Solution {
public void solveSudoku(char[][] board) {
// 三个布尔数组 表明 行, 列, 还有 3*3 的方格的数字是否被使用过
boolean[][] rowUsed = new boolean[9][10];
boolean[][] colUsed = new boolean[9][10];
boolean[][][] boxUsed = new boolean[3][3][10];
// 初始化
for(int row = 0; row < board.length; row++){
for(int col = 0; col < board[0].length; col++) {
int num = board[row][col] - '0';
if(1 <= num && num <= 9){
rowUsed[row][num] = true;
colUsed[col][num] = true;
boxUsed[row/3][col/3][num] = true;
}
}
}
// 递归尝试填充数组
recusiveSolveSudoku(board, rowUsed, colUsed, boxUsed, 0, 0);
}
private boolean recusiveSolveSudoku(char[][]board, boolean[][]rowUsed, boolean[][]colUsed, boolean[][][]boxUsed, int row, int col){
// 边界校验, 如果已经填充完成, 返回true, 表示一切结束
if(col == board[0].length){
col = 0;
row++;
if(row == board.length){
return true;
}
}
// 是空则尝试填充, 否则跳过继续尝试填充下一个位置
if(board[row][col] == '.') {
// 尝试填充1~9
for(int num = 1; num <= 9; num++){
boolean canUsed = !(rowUsed[row][num] || colUsed[col][num] || boxUsed[row/3][col/3][num]);
if(canUsed){
rowUsed[row][num] = true;
colUsed[col][num] = true;
boxUsed[row/3][col/3][num] = true;
board[row][col] = (char)('0' + num);
if(recusiveSolveSudoku(board, rowUsed, colUsed, boxUsed, row, col + 1)){
return true;
}
board[row][col] = '.';
rowUsed[row][num] = false;
colUsed[col][num] = false;
boxUsed[row/3][col/3][num] = false;
}
}
} else {
return recusiveSolveSudoku(board, rowUsed, colUsed, boxUsed, row, col + 1);
}
return false;
}
}
作者:I_use_java
链接:link
来源:力扣(LeetCode)
4)自己的优化代码
class Solution {
boolean[][] Cvisited =new boolean[9][9];//行
boolean[][] Rvisited =new boolean[9][9];//列
boolean[][][] CRvisited =new boolean[3][3][9];//3*3
int nexti=0,nextj=0;
public boolean backpack(int i,int j,char[][] board){
if(i>=9)return true;
if(board[i][j]!='.'){
if(j<8){nexti=i;nextj=j+1;}
if(j==8){nexti=i+1;nextj=0;}
if(backpack(nexti,nextj,board))return true;
return false;
}
else{
for(int k=0;k<9;k++){
if(IsVisited(i,j,k))continue;
board[i][j]=(char)(k+'1');
makeVisited(i,j,board);
if(j<8){nexti=i;nextj=j+1;}
if(j==8){nexti=i+1;nextj=0;}
if(backpack(nexti,nextj,board))return true;
makeUnVisited(i,j,board);
board[i][j]='.';
}
return false;
}
}
public boolean IsVisited(int i,int j,int k){
return Cvisited[i][k]||Rvisited[j][k]||CRvisited[i/3][j/3][k];
}
public void makeVisited(int i,int j,char[][] board){
Cvisited[i][board[i][j]-'1']=true;
Rvisited[j][board[i][j]-'1']=true;
CRvisited[i/3][j/3][board[i][j]-'1']=true;
}
public void makeUnVisited(int i,int j,char[][] board){
Cvisited[i][board[i][j]-'1']=false;
Rvisited[j][board[i][j]-'1']=false;
CRvisited[i/3][j/3][board[i][j]-'1']=false;
}
public void solveSudoku(char[][] board) {
for(int i=0;i<9;i++){
for(int j=0;j<9;j++){
if(board[i][j]!='.'){
makeVisited(i,j,board);
}
}
}
backpack(0,0,board);
}
}
5)学到的东西
回溯思想 1-9一个个试
改进思路:
(1)用空间换时间,每行、每列、每个小方块做备忘录,大大提高效率
(2)先初始化,之后遇到不是’.'的直接跳过即可
15、N 皇后(51、Hard)
1)题目要求
示例:
输入:4
输出:[
[".Q…", // 解法 1
“…Q”,
“Q…”,
“…Q.”],
["…Q.", // 解法 2
“Q…”,
“…Q”,
“.Q…”]
]
解释: 4 皇后问题存在两个不同的解法。
提示:
皇后彼此不能相互攻击,也就是说:任何两个皇后都不能处于同一条横行、纵行或斜线上。
2)我的解法
class Solution {
List<List<String>> result=new ArrayList<>();
boolean[] Rvisited;//列
boolean[] LXvisited;//左斜线
boolean[] RXvisited;//右斜线
int N=0;
StringBuilder s=new StringBuilder();
List<String> temp=new ArrayList<>();
public void backpack(int i){
if(i>=N){
result.add(new ArrayList<String>(temp));
return;
}
for(int j=0;j<N;j++){
if(isVisited(i,j))continue;
for(int k=0;k<N;k++){
if(k==j)s.append("Q");
else s.append(".");
}
temp.add(s.toString());
for(int k=0;k<N;k++)s.deleteCharAt(s.length()-1);
Rvisited[j]=true;
RXvisited[j-i+N-1]=true;
LXvisited[i+j]=true;
backpack(i+1);
Rvisited[j]=false;
RXvisited[j-i+N-1]=false;
LXvisited[i+j]=false;
temp.remove(temp.size()-1);
}
return ;
}
public boolean isVisited(int i,int j){
return Rvisited[j]||LXvisited[i+j]||RXvisited[j-i+N-1];
}
public List<List<String>> solveNQueens(int n) {
N=n;
Rvisited=new boolean[n];
RXvisited=new boolean[2*n-1];
LXvisited=new boolean[2*n-1];
backpack(0);
return result;
}
}
3)其他解法
1、
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
import java.util.List;
public class Solution {
private int n;
// 记录某一列是否放置了皇后
private boolean[] col;
// 记录主对角线上的单元格是否放置了皇后
private boolean[] sub;
// 记录了副对角线上的单元格是否放置了皇后
private boolean[] main;
private List<List<String>> res;
public List<List<String>> solveNQueens(int n) {
res = new ArrayList<>();
if (n == 0) {
return res;
}
// 设置成员变量,减少参数传递,具体作为方法参数还是作为成员变量,请参考团队开发规范
this.n = n;
this.col = new boolean[n];
this.sub = new boolean[2 * n - 1];
this.main = new boolean[2 * n - 1];
Deque<Integer> path = new ArrayDeque<>();
dfs(0, path);
return res;
}
private void dfs(int row, Deque<Integer> path) {
if (row == n) {
// 深度优先遍历到下标为 n,表示 [0.. n - 1] 已经填完,得到了一个结果
List<String> board = convert2board(path);
res.add(board);
return;
}
// 针对下标为 row 的每一列,尝试是否可以放置
for (int j = 0; j < n; j++) {
if (!col[j] && !sub[row + j] && !main[row - j + n - 1]) {
path.addLast(j);
col[j] = true;
sub[row + j] = true;
main[row - j + n - 1] = true;
dfs(row + 1, path);
main[row - j + n - 1] = false;
sub[row + j] = false;
col[j] = false;
path.removeLast();
}
}
}
private List<String> convert2board(Deque<Integer> path) {
List<String> board = new ArrayList<>();
for (Integer num : path) {
StringBuilder row = new StringBuilder();
row.append(".".repeat(Math.max(0, n)));
row.replace(num, num + 1, "Q");
board.add(row.toString());
}
return board;
}
}
2、HashSet
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
import java.util.HashSet;
import java.util.List;
import java.util.Set;
public class Solution {
private Set<Integer> col;
private Set<Integer> sub;
private Set<Integer> main;
private int n;
private List<List<String>> res;
public List<List<String>> solveNQueens(int n) {
this.n = n;
res = new ArrayList<>();
if (n == 0) {
return res;
}
col = new HashSet<>();
sub = new HashSet<>();
main = new HashSet<>();
Deque<Integer> path = new ArrayDeque<>();
dfs(0, path);
return res;
}
private void dfs(int row, Deque<Integer> path) {
if (row == n) {
List<String> board = convert2board(path);
res.add(board);
return;
}
// 针对每一列,尝试是否可以放置
for (int i = 0; i < n; i++) {
if (!col.contains(i) && !sub.contains(row + i) && !main.contains(row - i)) {
path.addLast(i);
col.add(i);
sub.add(row + i);
main.add(row - i);
dfs(row + 1, path);
main.remove(row - i);
sub.remove(row + i);
col.remove(i);
path.removeLast();
}
}
}
private List<String> convert2board(Deque<Integer> path) {
List<String> board = new ArrayList<>();
for (Integer num : path) {
StringBuilder row = new StringBuilder();
row.append(".".repeat(Math.max(0, n)));
row.replace(num, num + 1, "Q");
board.add(row.toString());
}
return board;
}
}
作者:liweiwei1419
链接:link
来源:力扣(LeetCode)
4)自己的优化代码
class Solution {
List<List<String>> result=new ArrayList<>();
boolean[] Rvisited;//列
boolean[] LXvisited;//左斜线
boolean[] RXvisited;//右斜线
int N=0;
StringBuilder s=new StringBuilder();
List<String> temp=new ArrayList<>();
public void backpack(int i){
if(i>=N){
result.add(new ArrayList<String>(temp));
return;
}
for(int j=0;j<N;j++){
if(isVisited(i,j))continue;
for(int k=0;k<N;k++){
if(k==j)s.append("Q");
else s.append(".");
}
temp.add(s.toString());
for(int k=0;k<N;k++)s.deleteCharAt(s.length()-1);
Rvisited[j]=true;
RXvisited[j-i+N-1]=true;
LXvisited[i+j]=true;
backpack(i+1);
Rvisited[j]=false;
RXvisited[j-i+N-1]=false;
LXvisited[i+j]=false;
temp.remove(temp.size()-1);
}
return ;
}
public boolean isVisited(int i,int j){
return Rvisited[j]||LXvisited[i+j]||RXvisited[j-i+N-1];
}
public List<List<String>> solveNQueens(int n) {
N=n;
Rvisited=new boolean[n];
RXvisited=new boolean[2*n-1];
LXvisited=new boolean[2*n-1];
backpack(0);
return result;
}
}
5)学到的东西
回溯思想
多弄点备忘录、找规律