ALS推荐算法简介

ALS(交替最小二乘法)

ALS (Alternating Least Squares) 交替最小二乘法。ALS 的核心是：打分矩阵R是近似低秩的。换句话说，一个打分矩阵 R 可以用两个小矩阵和的乘积来近似。其基本原理是如果有两个变量需要确定，那ALS先固定第一个变量，然后求解第二个变量。之后固定第二个变量，求解第一个变量。如此交替迭代直至收敛或者达到最大迭代次数。
ALS属于混合CF,同时考虑了user和item两个方面

1.1 原理推导

在推荐系统中，以淘宝为例，在建立用户-物品矩阵的时候，我们会发现物品种类异常丰富，在数据挖掘中，体现为数据的维度非常高，那么把所有的这些用户-物品数据建立一个评分矩阵，将其全部载入内存，然后计算用户vs用户的相似度，或者计算物品vs物品的相似度，导致计算量非常庞大。
那么如何给我们高维的数据降维呢？
ALS假设我们的评分矩阵能分解为两个小矩阵的乘积，“打分矩阵R(mn)”就可以由“用户喜好特征矩阵U(mk)”和“产品特征矩阵V(n*k)
$$R=U\ast V^T$$

M是用户数，n是物品数，k为隐含特征数

2.1.1 ALS

了解ALS的原理后，我们定义ALS的损失函数, 使得目标最小化：
$$L=(R-U{V}^T{)}^2$$
那么有两个未知变量该如何求解呢？
假设在这里只有一个未知变量，我们可以通过给未知参数求导，使得导数为0，便可求解。那么在这里，我们假设其中一个变量已知V，求解出另一个参数U后，然后假设U已知，然后求解V，如此不断迭代，直到满足阈值条件为止。这就是所谓的交替最小二乘法
首先，我们固定变量V, 对U进行求导，有：
$$\frac{\partial L}{\partial U}=-2\ast (R-U{V}^T{)}^2$$
$$=>U{V}^{T}V=RV$$
$$=>U=RV\ast (V^{T}V{)}^{-1}$$
同理，我们固定变量U, 对V进行求导，有：
$$\frac{\partial L}{\partial V}=-2\ast U^T\ast (R-U\ast V^T{)}^2=0$$
$$=>U^{T}R=U^{T}U{V}^T$$
$$=>V^T=(U^{T}U{)}^{-}1U^{T}R$$
$$=>V=R^{T}U(U^{T}U{)}^{-1}$$
是实对称矩阵，实对称阵的转置等于本身( $A^T=A$)，所以( U^TU)直接去掉转置符号。

2.1.2 ALS-L2正则化

加入正则化项是为了防止过拟合，正则化项对参数进行惩罚，缩小参数范围，从而提高模型的泛化能力。
在基础的ALS代价函数上上加入一个L2正则化项，那么ALS-L2为：
$$L_{ALS-L2}=(R-U{V}^T{)}^2+\lambda (|U{|}^2+|V{|}^2)$$

按照7.1.1中推导算法原则，对U,V进行求解
首先，我们固定变量V, 对U进行求导，有：
$$\frac{\partial L}{\partial U}=-2\ast (R-U{V}^T)V+2\lambda U=0$$
$$=>U{V}^{T}V+\lambda U=RV$$
$$=>U=RV(V^{T}V+\lambda I)$$
$$U(i,:)=R(i,:)\ast V\ast (V^{T}V+\lambda {)}^{-1}i是用户数$$

同理，我们固定变量U, 对V进行求导，有：
$$\frac{\partial L}{\partial V}=-2\ast U^T(R-U\ast V^T)+2\lambda V^T=0$$
$$=>U^{T}R=U^{T}U{V}^T+\lambda V^T$$
$$=>V^T=(U^{T}U+\lambda {)}^{-}1U^{T}R$$
$$=>V=R^{T}U(U^{T}U+\lambda {)}^{-1}$$
$$=>V(i,:)=R(i,:{)}^T\ast U\ast (U^{T}U+\lambda {)}^T$$

2.1.3 Stochastic Gradient ALS

$$R=G_u+b_u+b_v+U^{T}V$$
Gu是全局的偏置，bu是U的偏置向量，bv是V的偏置向量
定义损失函数
$$L=(R-G_u+b_u+b_v+U^{T}V)2+{\lambda }_1||b_v|{|}^2+{\lambda }_2\ast ||b_u|{|}^2+{\lambda }_3\ast ||U|{|}^2+{\lambda }_4\ast ||V|{|}^2$$
$$L=\sum _{u,i}(r_{ui}-(u+b_u+b_i+x{}_u{}^t{y}_i){)}^2$$
$$+{\lambda }_{xb}\sum _u||b_u|{|}^2+{\lambda }_{yb}\sum _i||b_i|{|}^2$$
$$+{\lambda }_{xf}\sum _u||x_u|{|}^2+{\lambda }_{yf}\sum _u||y_i|{|}^2$$

$$b_u=b_u-\eta \frac{\partial L}{\partial b_u}$$
令
$$e_{ui}=r_{ui}-(\mu +b_u+b_i+x_u^T\ast y_i)$$
则
$$\frac{\partial L}{\partial b_u}=2e_{ui}(-1)+2{\lambda }_{xb}{b}_u$$
以此类推
$$b_u=b_u+\eta (e_{ui}-{\lambda }_{xb}{b}_u)$$
$$b_i=b_i+\eta (e_{ui}-{\lambda }_{yb}{b}_i)$$
$$x_u=x_u+\eta (e_{ui}{y}_i-{\lambda }_{xf}{x}_u)$$
$$y_i=y_i+\eta (e_{ui}{x}_u-{\lambda }_{yf}{y}_i)$$

=

2.1.4 隐式反馈(Implicit Feedback )

用户给商品评分是个非常简单粗暴的用户行为。在实际的电商网站中，还有大量的用户行为，同样能够间接反映用户的喜好，比如用户的购买记录、搜索关键字，甚至是鼠标的移动。我们将这些间接用户行为称之为隐式反馈（implicit feedback），以区别于评分这样的显式反馈（explicit feedback）。
隐式反馈有以下几个特点：
1.没有负面反馈（negative feedback）。用户一般会直接忽略不喜欢的商品，而不是给予负面评价。
2.隐式反馈包含大量噪声。比如，电视机在某一时间播放某一节目，然而用户已经睡着了，或者忘了换台。
3.显式反馈表现的是用户的喜好（preference），而隐式反馈表现的是用户的信任（confidence）。比如用户最喜欢的一般是电影，但观看时间最长的却是连续剧。大米购买的比较频繁，量也大，但未必是用户最想吃的食物。
4.隐式反馈非常难以量化。
(1) ALS-WR算法
ALS with Weighted-λ-Regularization，加权正则化交替最小二乘法
首先将用户反馈(喜好)分类：

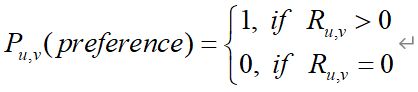
表示原始量化值，比如观看电影的时间。
但是喜好是有程度差异的，因此需要定义程度系数：
$$C_{u,v}=1+\alpha R_{u,v}$$
这里，1表示最低信任度， 表示根据用户行为所增加的信任度(confidence)。
那么，可以定义损失函数如下：
$$mi{n}_{u,v}L=C_{u,v}(P_{u,v}-U_u{V}_v^T{)}^2+\lambda (|U_u{|}^2+|V_v{|}^2)$$

其中， $u\in (1,2,3,4,...,m),v\in (1,2,3,...,n)$
经过计算有：
$$U_u=(V^T{C}^{u}V+\lambda I{)}^{-}1V^T{C}^u{R}_U$$
$$V_v=(U^T{C}^{v}U+\lambda I{)}^{-}1U^T{C}^v{R}_v$$

其中Cu是n×n的对角矩阵，Cv是m×m的对角矩阵；
注：
除此之外，我们还可以使用指数函数来定义
$$C_{u,v}=1+\alpha log(1+R_{u,v}/ϵ)$$

参考链接：
[1] 原理介绍：https://github.com/ceys/jdml/wiki/ALS
[2] 针对wiki中的公式显示整理：http://www.fuqingchuan.com/2015/03/812.html
[3] spark mllib及代码实例:https://spark.apache.org/docs/latest/mllib-collaborative-filtering.html
[4]http://xueshu.baidu.com/usercenter/paper/show?paperid=976d8536bd832358b4cd6a26f3c624be&site=xueshu_se
[5] https://blog.csdn.net/wguangliang/article/details/51539710
[6] https://www.cnblogs.com/zlslch/p/7478395.html

2. 优缺点

• 优点：

1. 它是一个离线算法。
2. ALS适合大数据并发场景，效率非常高。
3. 无法准确评估新加入的用户或商品。依然存在冷启动问题
4. ALS是一个凸优化问题
5. 较SVD分解而言，可解决数据稀疏问题

• 缺点：
  在对于隐变量个数选择比较敏感(k越大越精确，但同时会导致计算时间变长)。

---

edited by ：Eshter YUU
date:2020/04/12 22:29