弗洛伊德算法Floyd

全知识整理目录

数据结构整理的目录包括了许多的数据结构相关知识。

---

目录

概述

算法过程

关键代码的实现 

总结

参考 

---

概述

Floyd算法是什么？

Floyd算法也是动态规划的求最短路径，但不同于Dijkstra算法，Floyd算法可以求权值为负的边，其主要代码的思想是三层for循环，所以时间复杂度为O()。

算法过程

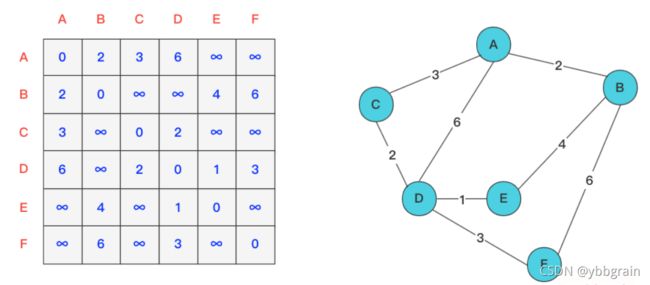
首先floyd算法，是将所有顶点都当成一个独立的个体，只能访问到相临的结点。以此绘制一张表，初始表，仅仅表示的是相临边之间的距离。

然后插入第一个顶点。例如插入A，然后C-B，D-B，B-C,B-D，的距离就会发生变化，更新表。

之后再插入第二顶点。例如插入B，按表中的行列依次对比，是否发生变化，变化的可能比原来的小，也可能比原来的大，比原来小的更新表。

后续插入C,D,E,F都是遵循次规律，依次更新表，而插入最后一个顶点之后，得到的表就是最终的最短路径。

关键代码的实现 

int dist[][] = {
				{ 0, 2, 3, 6, max, max }, 
				{ 2, 0, max, max,4, 6 }, 
				{ 3, max, 0, 2, max, max },
				{ 6, max, 2, 0, 1, 3 }, 
				{ max, 4, max, 1, 0, max }, 
				{ max, 6, max, 3, max, 0 } };//图

for (int k = 0; k < 6; k++)// 加入第k个节点进行计算
		{
			for (int i = 0; i < 6; i++)// 每加入一个点都要枚举图看看有没有可以被更新的
			{
				for (int j = 0; j < 6; j++)
				{
					dist[i][j] = Math.min(dist[i][j], dist[i][k] + dist[k][j]);
				}
			}
		}

总结

• Floyd算法，的核心就是不断地插入顶点，在每次插入之后更新表。
• 关键代码是3个for循环，可以得到时间复杂度为 O()。

参考 

多源最短路径算法—Floyd算法