快速入门深度学习1（用时1h）——MXNet版本

写在最前面

之前计划一天看一点，还是高估了自己，断断续续的看到啥时候去了，干脆花一天快速入门

学习资料（《动手学深度学习》文档）：http://zh.gluon.ai/chapter_how-to-use/how-to-use.html

0.内容与结构

最基础的概念和技术：第1章至第3章
现代深度学习技术：第4章至第6章
根据兴趣选择阅读：第7章至第10章

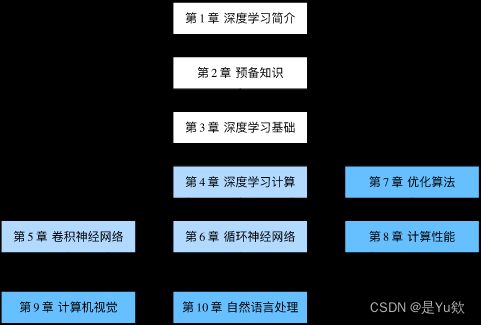
1.深度学习简介

1.1 问题引入

问题：判断图片是否有猫

简化：
① 假设所有图像的高和宽都是同样的400像素大小，一个像素由红绿蓝三个值构成，那么一张图像就由近50万个数值表示。
② 哪些数值隐藏着我们需要的信息呢？是所有数值的平均数，还是四个角的数值，抑或是图像中的某一个特别的点？
③ 事实上，要想解读图像中的内容，需要寻找仅仅在结合成千上万的数值时才会出现的特征，如边缘、质地、形状、眼睛、鼻子等，最终才能判断图像中是否有猫。

1.2 思路：逆向思考

与其设计一个解决问题的程序，不如从最终的需求入手来寻找一个解决方案。

机器学习和深度学习应用共同的核心思想：“用数据编程”。

收集一些已知包含猫与不包含猫的真实图像
目标：转化成如何从这些图像入手，得到一个可以推断出图像中是否有猫的函数。
这个函数的形式通常通过我们的知识来针对特定问题选定。
例如，我们使用一个二次函数来判断图像中是否有猫，但是像二次函数系数值这样的函数参数的具体值则是通过数据来确定。

机器学习：一门讨论各式各样的适用于不同问题的函数形式，以及如何使用数据来有效地获取函数参数具体值的学科。
深度学习：机器学习中的一类函数，它们的形式通常为多层神经网络，复杂高维度数据的主要方法。

1.3 跳过

起源、发展、成功案例

1.4 特点

机器学习：研究如何使计算机系统利用经验改善性能。表征学习关注如何自动找出表示数据的合适方式，以便更好地将输入变换为正确的输出
深度学习：具有多级表示的表征学习方法。在每一级（从原始数据开始），深度学习通过简单的函数将该级的表示变换为更高级的表示。
可以看作是由许多简单函数复合而成的函数。当这些复合的函数足够多时，深度学习模型就可以表达非常复杂的变换。

深度学习可以逐级表示越来越抽象的概念或模式。
以图像为例，它的输入是一堆原始像素值。深度学习模型中，图像可以逐级表示为特定位置和角度的边缘、由边缘组合得出的花纹、由多种花纹进一步汇合得到的特定部位的模式等。
最终，模型能够较容易根据更高级的表示完成给定的任务，如识别图像中的物体。
值得一提的是，作为表征学习的一种，深度学习将自动找出每一级表示数据的合适方式。

因此，深度学习的一个外在特点是端到端的训练。也就是说，并不是将单独调试的部分拼凑起来组成一个系统，而是将整个系统组建好之后一起训练。
自动优化的逐级过滤器。

从含参数统计模型转向完全无参数的模型。
当数据非常稀缺时，需要通过简化对现实的假设来得到实用的模型。
当数据充足时，能更好地拟合现实的无参数模型来替代这些含参数模型。可以得到更精确的模型，尽管需要牺牲一些可解释性。

深度学习：对非最优解的包容、对非凸非线性优化的使用，以及勇于尝试没有被证明过的方法。

1.5 小结

机器学习研究如何使计算机系统利用经验改善性能。它是人工智能领域的分支，也是实现人工智能的一种手段。
作为机器学习的一类，表征学习关注如何自动找出表示数据的合适方式。
深度学习是具有多级表示的表征学习方法。它可以逐级表示越来越抽象的概念或模式。

深度学习使用场景：虽有许多展示如何解决问题的样例，但缺少自动解决问题的算法

2.预备知识（MXNet版本，学错了。。。。）

2.1 获取和运行本书的代码

http://zh.gluon.ai/chapter_prerequisite/install.html

2.2 数据操作

2.2.1 略过

基础的python，略过
http://zh.gluon.ai/chapter_prerequisite/ndarray.html

2.2.1. 创建NDArray

之前创建的向量和矩阵都是特殊的张量

2.2.2. 运算

2.2.3. 广播机制
当对两个形状不同的NDArray按元素运算时，可能会触发广播（broadcasting）机制：先适当复制元素使这两个NDArray形状相同后再按元素运算。

解析：由于A和B分别是3行1列和1行2列的矩阵，如果要计算A + B，那么A中第一列的3个元素被广播（复制）到了第二列，而B中第一行的2个元素被广播（复制）到了第二行和第三行。如此，就可以对2个3行2列的矩阵按元素相加。

A
 [[0.]
  [1.]
  [2.]]
 <NDArray 3x1 @cpu(0)>
 
 B
 [[0. 1.]]
 <NDArray 1x2 @cpu(0)>
 
A + B
[[0. 1.]
 [1. 2.]
 [2. 3.]]
<NDArray 3x2 @cpu(0)>

2.2.4. 索引
2.2.5. 运算的内存开销
Python自带的id函数：如果两个实例的ID一致，那么它们所对应的内存地址相同；反之则不同。

2.2.6. NDArray和NumPy相互变换
可以通过array函数和asnumpy函数令数据在NDArray和NumPy格式之间相互变换。

import numpy as np

P = np.ones((2, 3))
D = nd.array(P)
D

D.asnumpy()

2.2.2 小结

NDArray是MXNet中存储和变换数据的主要工具。
可以轻松地对NDArray创建、运算、指定索引，并与NumPy之间相互变换。

2.3 自动求梯度

在深度学习中，我们经常需要对函数求梯度（gradient）。本节将介绍如何使用MXNet提供的autograd模块来自动求梯度。

2.3.1 简单例子

对函数 $y=2{\mathbf{x}}^{\top }\mathbf{x}$ 求关于列向量 $\mathbf{x}$ 的梯度。我们先创建变量$x$，并赋初值。

In [2]:

x = nd.arange(4).reshape((4, 1))
x

Out[2]:

[[0.]
 [1.]
 [2.]
 [3.]]
<NDArray 4x1 @cpu(0)>

为了求有关变量x的梯度，我们需要先调用attach_grad函数来申请存储梯度所需要的内存。

In [3]:

x.attach_grad()

下面定义有关变量x的函数。为了减少计算和内存开销，默认条件下MXNet不会记录用于求梯度的计算。我们需要调用record函数来要求MXNet记录与求梯度有关的计算。

In [4]:

with autograd.record():
    y = 2 * nd.dot(x.T, x)

由于x的形状为（4, 1），y是一个标量。接下来我们可以通过调用backward函数自动求梯度。需要注意的是，如果y不是一个标量，MXNet将默认先对y中元素求和得到新的变量，再求该变量有关x的梯度。

In [5]:

y.backward()

函数 y = $2{\mathbf{x}}^{\top }\mathbf{x}$ 关于$\mathbf{x}$ 的梯度应为$4\mathbf{x}$。现在我们来验证一下求出来的梯度是正确的。

In [6]:

assert (x.grad - 4 * x).norm().asscalar() == 0
x.grad

Out[6]:

[[ 0.]
 [ 4.]
 [ 8.]
 [12.]]
<NDArray 4x1 @cpu(0)>

2.3.2 训练模式和预测模式

从上面可以看出，在调用record函数后，MXNet会记录并计算梯度。此外，默认情况下autograd还会将运行模式从预测模式转为训练模式。这可以通过调用is_training函数来查看。

In [7]:

print(autograd.is_training())
with autograd.record():
    print(autograd.is_training())

False
True

在有些情况下，同一个模型在训练模式和预测模式下的行为并不相同。我们会在后面的章节（如“丢弃法”一节）详细介绍这些区别。

2.3.3 对Python控制流求梯度

使用MXNet的一个便利之处是，即使函数的计算图包含了Python的控制流（如条件和循环控制），我们也有可能对变量求梯度。

考虑下面程序，其中包含Python的条件和循环控制。需要强调的是，这里循环（while循环）迭代的次数和条件判断（if语句）的执行都取决于输入a的值。

对输入的a不断的乘以2直到大于1000输出，其实就是一个类似线性函数。（评论大佬解读）

In [8]:

def f(a):
    b = a * 2
    while b.norm().asscalar() < 1000:
        b = b * 2
    if b.sum().asscalar() > 0:
        c = b
    else:
        c = 100 * b
    return c

我们像之前一样使用record函数记录计算，并调用backward函数求梯度。

In [9]:

a = nd.random.normal(shape=1)
a.attach_grad()
with autograd.record():
    c = f(a)
c.backward()

我们来分析一下上面定义的f函数。事实上，给定任意输入a，其输出必然是 f(a) = x * a的形式，其中标量系数x的值取决于输入a。由于c = f(a)有关a的梯度为x，且值为c / a，我们可以像下面这样验证对本例中控制流求梯度的结果的正确性。

In [10]:

a.grad == c / a

Out[10]:

[1.]
<NDArray 1 @cpu(0)>

2.3.4. 小结

MXNet提供autograd模块来自动化求导过程。
MXNet的autograd模块可以对一般的命令式程序进行求导。
MXNet的运行模式包括训练模式和预测模式。我们可以通过autograd.is_training()来判断运行模式。

2.4. 查阅文档（跳过）

http://zh.gluon.ai/chapter_prerequisite/lookup-api.html