【EI复现】基于元模型优化算法的主从博弈多虚拟电厂动态定价和能量管理(Matlab代码实现)
欢迎来到本博客❤️❤️
博主优势:博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
本文目录如下:
目录
1 概述
2 运行结果
3 参考文献
4 Matlab代码、数据、文章
1 概述
目前,国内外学者从单利益主体出发,针对虚拟电厂的发电调度[2-3]、竞价模式[4-5]等方面已经做
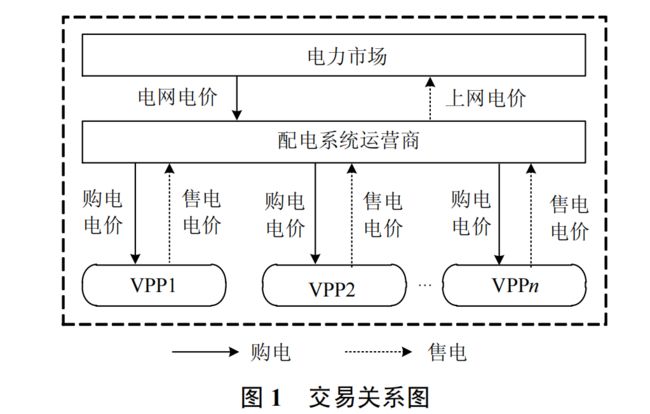
了不少研究。如果有更多社会资本参与电力市场,各 VPP 都将可能隶属于不同的利益主体。在个体理性的驱使下,各利益主体追求自身利益最大化,传统的单一主体的优化调度方法将很难适用[6]。基于上述考虑,目前已有研究利用博弈论分析 VPP 之间以及内部不同主体的利益均衡关系[7-11]。然而上述文献多数集中在给定交易电价的前提下,研究 VPP之 间 的 博 弈 关 系 。 本 文 引 入 配 电 网 运 营 商(distribution system operator,DSO),建立 DSO 与多VPP 的一主多从博弈优化模型,研究 DSO 动态定价与 VPP 运行策略的相互影响,实现多虚拟电厂的能量管理。
主从博弈模型为一类均衡约束均衡优化问题,其中下层博弈问题为上层优化问题的一个约束条
件,因此该模型呈复杂性、非线性、非凸性[12]。目前主从博弈均衡解的求解方法主要有基于 KarushKuhn-Tucker (KKT)条件的数值优化方法[13-15]和启发式智能算法[16-19]。KKT 条件法能够简化模型,但要求下层模型为凸规划问题,且上层需要下层所有的参数信息,涉及到隐私问题。而启发式智能算法上下层之间仅需交换少量信息,能够保护下层隐私,但其需要大量调用下层博弈模型,计算繁复,效率低下。
为应对上述问题,本文提出一种基于元模型的优化算法,首次将 Kriging 元模型引入求解主从博
弈均衡解,以期在保护 VPP 隐私的同时,提高计算效率。基于元模型的优化算法是一种基于历史数据来驱动样本点的加入从而逼近局部或全局最优解的优化机制,能够改善传统启发式智能算法需要繁复数值模拟的缺陷,目前在飞行器设计等航空航天领域的应用[20]最为广泛,在电力系统方面也有初步的应用。文献[21]用 Kriging 元模型拟合随机风速和电力系统暂态仿真随机响应。文献[22]和[23]用Kriging 元模型代替潮流计算,分别研究主动配电网的最优经济运行和无功优化。
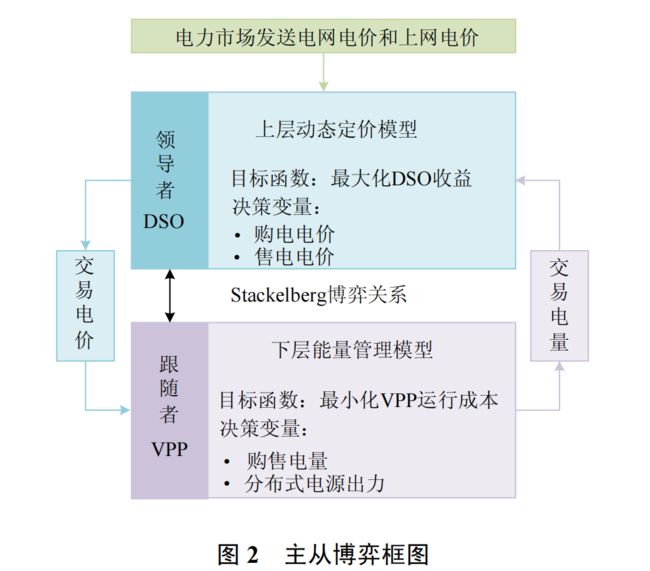
综上,本文考虑 DSO 和 VPP 具有不同的利益需求,建立基于主从博弈多 VPP 动态定价和能量管
理模型。提出基于 Kriging 元模型的博弈均衡算法,在求解过程中建立 Kriging 元模型替代 VPP 内部的能量管理模型,利用粒子群优化算法搜索优异采样点,更新修正 Kriging 模型,避免对下层博弈模型的繁复计算,提高寻优效率。最后通过算例分析,验证本文所建模型和所提算法的有效性。
详细文章讲解见第4部分。
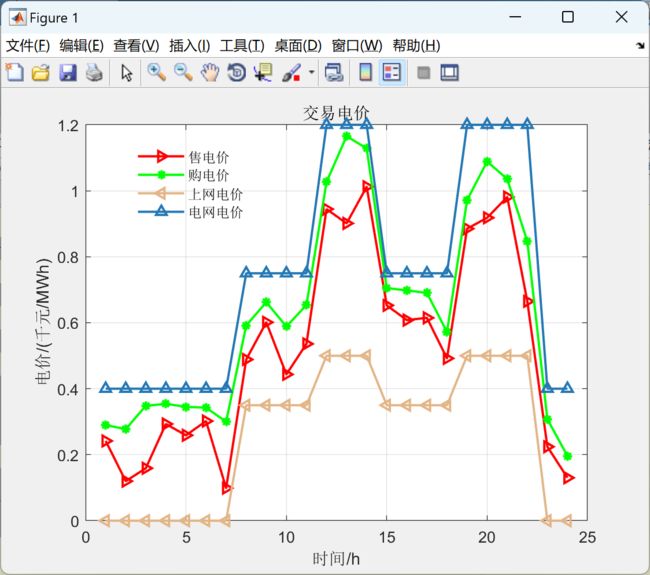
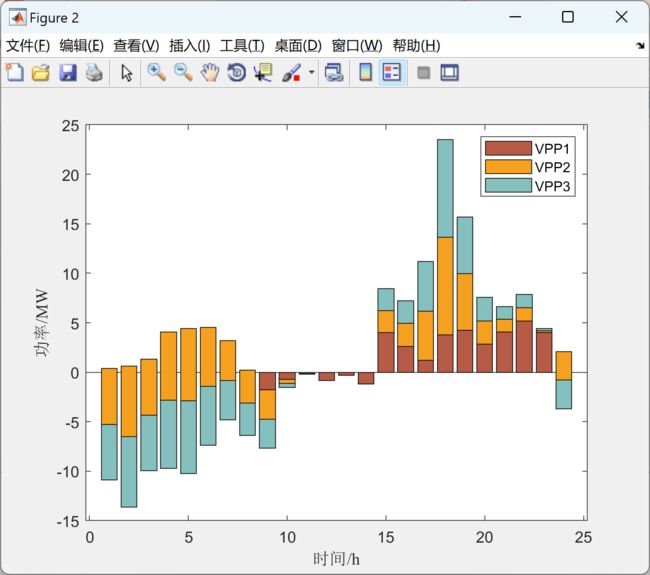
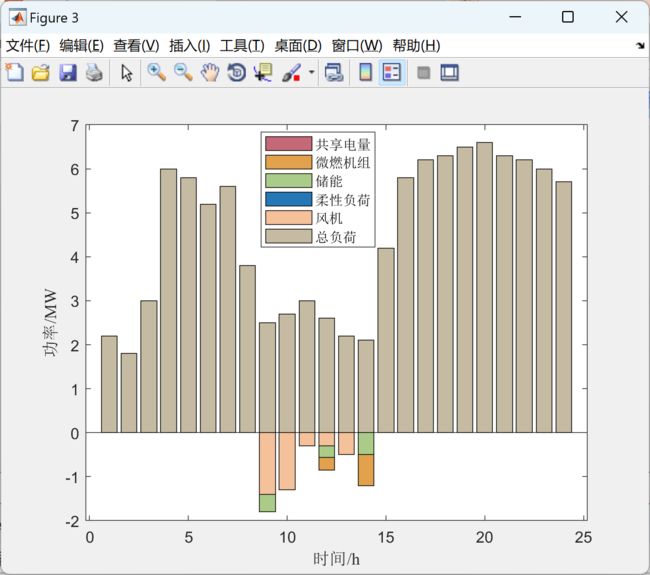
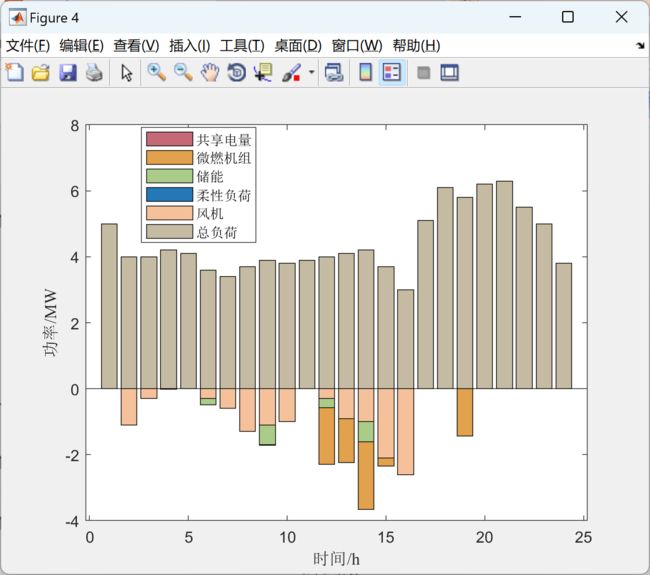
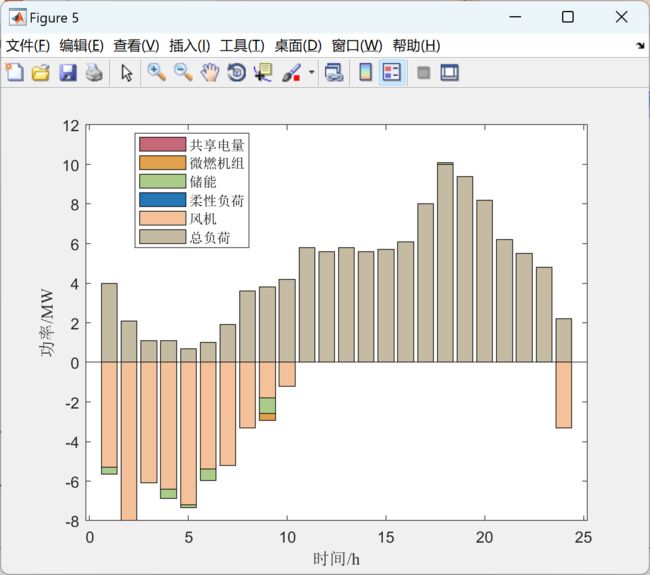
2 运行结果
部分代码:
function [P_VPP_s,P_VPP_b,Out]=Fun_VPP1(lambda_DAb,lambda_DAs)
%计算下层VPP交易子流程
%% 决策变量初始化
P_VPP_b=sdpvar(1,24); %VPP向运营商的购电量
P_VPP_s=sdpvar(1,24); %VPP向运营商的售电量
P_VPP=sdpvar(1,24); %VPP与运营商的交易电量
P_MT=sdpvar(1,24); %VPP中的MT的发电功率
P_ES=sdpvar(1,24); %VPP中的储能充放电功率,正时为放电
P_IL=sdpvar(1,24); %VPP中的可中断负荷
P_W=sdpvar(1,24); %VPP中的实际风电出力
S_ES=sdpvar(1,24); %VPP中的储电设备的荷电状态
theta=binvar(1,24); %VPP与运营商的交易电量状态变量
%% 导入电负荷和风电出力
P_LD=[2.2,1.8,3,6,5.8,5.2,5.6,3.8,2.5,2.7,3,2.6,2.2,2.1,4.2,5.8,6.2,6.3,6.5,6.6,6.3,6.2,6,5.7];
P_Wmax=[2,1.5,1.6,1.8,1.3,0.6,2.8,3.3,3.9,4,3.3,2.9,2.7,2,0.2,3.2,5.1,3.1,1.8,2,1.3,1 2,3.8];
%% 导入约束条件
C=[];
C=[C,
P_VPP==P_VPP_b-P_VPP_s, %VPP与运营商的交易电量,正时为购买电量,负时为售卖电量
P_VPP+P_MT+P_ES+P_IL+P_W==P_LD, %VPP的内部电功率平衡约束
0<=P_VPP_s<=theta*10, %设定VPP与运营商的最大售卖电量为10MW
0<=P_VPP_b<=(1-theta)*10, %设定VPP与运营商的最大购买电量为10MW
0<=P_MT<=6, %MT的输出功率上下限限制
-3.5<=P_MT(2:24)-P_MT(1:23)<=3.5, %MT的爬坡约束
-0.6<=P_ES<=0.6, %储能的充放电上下限功率约束
S_ES(1)==0.4-P_ES(1)/1, %储能设备的0-1时段的SoC约束,取初始SoC为0.4
S_ES(2:24)==S_ES(1:23)-P_ES(2:24)/1, %储能设备的1-24时段的SoC约束
0.2<=S_ES<=0.9, %SoC状态上下限约束
S_ES(24)==0.4, %储能的末态SoC和初态值相等
0<=P_IL<=0.1*P_LD, %可中断负荷的上下限约束
0<=P_W<=P_Wmax, %风电机组出力上下限约束
];
%% 设定目标函数
C_MT=0.08*P_MT.^2+0.9*P_MT+1.2; %微型燃气轮机的发电成本
C_ES=0.05*P_ES.^2; %储能成本
C_IL=1.4*P_IL; %可中断负荷成本
C_VPP=sum(lambda_DAb.*P_VPP_b-lambda_DAs.*P_VPP_s)+sum(C_MT+C_ES+C_IL); %VPP的总运行成本
%% 求解器配置与求解
ops=sdpsettings('solver','cplex','verbose',0,'usex0',0);
ops.cplex.mip.tolerances.mipgap=1e-6;
result=solvesdp(C,C_VPP,ops);
%% 数据输出
P_VPP_b=double(P_VPP_b);
P_VPP_s=double(P_VPP_s);
Out = [P_VPP;P_MT;P_ES;P_IL;P_W;-P_LD];
end
function [P_VPP_s,P_VPP_b,Out]=Fun_VPP1(lambda_DAb,lambda_DAs)
%计算下层VPP交易子流程
%% 决策变量初始化
P_VPP_b=sdpvar(1,24); %VPP向运营商的购电量
P_VPP_s=sdpvar(1,24); %VPP向运营商的售电量
P_VPP=sdpvar(1,24); %VPP与运营商的交易电量
P_MT=sdpvar(1,24); %VPP中的MT的发电功率
P_ES=sdpvar(1,24); %VPP中的储能充放电功率,正时为放电
P_IL=sdpvar(1,24); %VPP中的可中断负荷
P_W=sdpvar(1,24); %VPP中的实际风电出力
S_ES=sdpvar(1,24); %VPP中的储电设备的荷电状态
theta=binvar(1,24); %VPP与运营商的交易电量状态变量
%% 导入电负荷和风电出力
P_LD=[2.2,1.8,3,6,5.8,5.2,5.6,3.8,2.5,2.7,3,2.6,2.2,2.1,4.2,5.8,6.2,6.3,6.5,6.6,6.3,6.2,6,5.7];
P_Wmax=[2,1.5,1.6,1.8,1.3,0.6,2.8,3.3,3.9,4,3.3,2.9,2.7,2,0.2,3.2,5.1,3.1,1.8,2,1.3,1 2,3.8];
%% 导入约束条件
C=[];
C=[C,
P_VPP==P_VPP_b-P_VPP_s, %VPP与运营商的交易电量,正时为购买电量,负时为售卖电量
P_VPP+P_MT+P_ES+P_IL+P_W==P_LD, %VPP的内部电功率平衡约束
0<=P_VPP_s<=theta*10, %设定VPP与运营商的最大售卖电量为10MW
0<=P_VPP_b<=(1-theta)*10, %设定VPP与运营商的最大购买电量为10MW
0<=P_MT<=6, %MT的输出功率上下限限制
-3.5<=P_MT(2:24)-P_MT(1:23)<=3.5, %MT的爬坡约束
-0.6<=P_ES<=0.6, %储能的充放电上下限功率约束
S_ES(1)==0.4-P_ES(1)/1, %储能设备的0-1时段的SoC约束,取初始SoC为0.4
S_ES(2:24)==S_ES(1:23)-P_ES(2:24)/1, %储能设备的1-24时段的SoC约束
0.2<=S_ES<=0.9, %SoC状态上下限约束
S_ES(24)==0.4, %储能的末态SoC和初态值相等
0<=P_IL<=0.1*P_LD, %可中断负荷的上下限约束
0<=P_W<=P_Wmax, %风电机组出力上下限约束
];
%% 设定目标函数
C_MT=0.08*P_MT.^2+0.9*P_MT+1.2; %微型燃气轮机的发电成本
C_ES=0.05*P_ES.^2; %储能成本
C_IL=1.4*P_IL; %可中断负荷成本
C_VPP=sum(lambda_DAb.*P_VPP_b-lambda_DAs.*P_VPP_s)+sum(C_MT+C_ES+C_IL); %VPP的总运行成本
%% 求解器配置与求解
ops=sdpsettings('solver','cplex','verbose',0,'usex0',0);
ops.cplex.mip.tolerances.mipgap=1e-6;
result=solvesdp(C,C_VPP,ops);
%% 数据输出
P_VPP_b=double(P_VPP_b);
P_VPP_s=double(P_VPP_s);
Out = [P_VPP;P_MT;P_ES;P_IL;P_W;-P_LD];
end
3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
[1]董雷,涂淑琴,李烨等.基于元模型优化算法的主从博弈多虚拟电厂动态定价和能量管理[J].电网技术,2020,44(03):973-983.DOI:10.13335/j.1000-3673.pst.2019.2244.