【零基础学习机器学习】线性回归
目录
线性回归介绍
求W值方法一:最小二乘法之正规方程
求W值方法二:最小二乘法之梯度下降
sklearn线性回归正规方程、梯度下降API
回归性能评估
sklearn回归评估API
线性回归实例
算法API使用建议
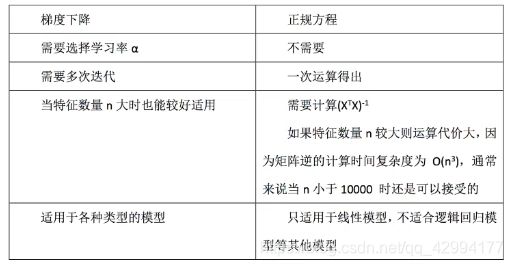
正规方程和梯度下降总结
过拟合以及欠拟合
定义
欠拟合原因及解决办法
过拟合原因及解决办法
回归问题解决过拟合的方式 - 岭回归(带有正则化的线性回归)
岭回归 - 带有正则化的线性回归
API
案例
线性回归LinearRegression与Ridge对比
回归算法 - 线性回归分析
线性回归实例
回归性能评估
线性回归介绍
回归问题的判定?
目标值是连续的
回归、神经网络属于迭代的算法。预测的时候有误差,所以每次都会一次次迭代,一次次减少误差。
那么优化的时候,尽量减少损失函数的值。要损失函数最小,就要寻找最优化的W值(权重)
求W值方法一:最小二乘法之正规方程
当特征数量很多,样本多的时候,不通用,求不到W。
求W值方法二:最小二乘法之梯度下降
梯度下降这种算法,是随机给出w值,通过梯度下降,调整到损失最小,取损失最小时的w值 。
sklearn线性回归正规方程、梯度下降API
回归系数就是w值(权重)
回归性能评估
sklearn回归评估API
sklearn.metrics.mean_squared_error
线性回归实例
1、sklearn线性回归正规方程、梯度下降API
2、波士顿放假数据集分析流程
数据特征:
案例分析流程:
案例演示:
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression, SGDRegressor
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error
def mylinear():
"""
线性回归直接预测房子价格
:return:
"""
# TODO 获取数据
lb = load_boston()
# TODO 分割数据集到训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)
# TODO 进行标准化处理,目标值处理。
# 特征值和目标值都必须进行标准化处理,实例化两个标准化API
std_x = StandardScaler()
x_train = std_x.fit_transform(x_train)
x_test = std_x.transform(x_test)
# 目标值
std_y = StandardScaler()
y_train = std_y.fit_transform(y_train.reshape(-1,1))
y_test = std_y.transform(y_test.reshape(-1,1))
# sklearn版本若是0.19的,std_y.fit_transform(y_train) 传入的y_train值必须是二维的
# sklearn版本若是0.19的,转换器,estimator(估计器),要求数据必须是二维 .reshape(-1,1)行不确定就填-1,列有一列
# sklearn版本若是0.18的,一维、二维都可以
# TODO estimator预测
# 方法一:正规方程求解方式预测结果
lr = LinearRegression()
lr.fit(x_train, y_train)
print("权重参数(回归系数)为:", lr.coef_)
# 预测测试集的房子价格,inverse_transform 转换为标准化之前的数据
y_lr_predict = lr.predict(x_test)
y_lr_predict = std_y.inverse_transform(y_lr_predict)
print("正规方程测试集中每个房子的预测价格:", y_lr_predict)
print("正规方程的均方误差:", mean_squared_error(std_y.inverse_transform(y_test), y_lr_predict))
# 方法二:梯度下降进行房价预测
sgd = SGDRegressor()
sgd.fit(x_train, y_train)
print("权重参数(回归系数)为:", sgd.coef_)
# 预测测试集的房子价格,inverse_transform 转换为标准化之前的数据
y_sgd_predict = sgd.predict(x_test)
y_sgd_predict = std_y.inverse_transform(y_sgd_predict)
print("梯度下降测试集中每个房子的预测价格:", y_sgd_predict)
print("梯度下降的均方误差:", mean_squared_error(std_y.inverse_transform(y_test), y_sgd_predict))
return None
if __name__ == '__main__':
mylinear()算法API使用建议
当数据量少的时候,数据较简单,用正规方程求解会更好。
当数据量大,几十万以上,用梯度下降求解会更好。
以下图是官网给的建议:
正规方程和梯度下降总结
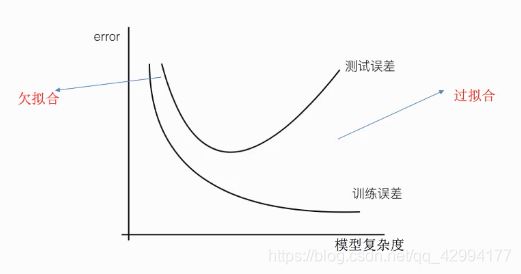
过拟合以及欠拟合
问题:
训练数据训练的很好啊,误差也不大,为什么在测试集上面有问题呢?
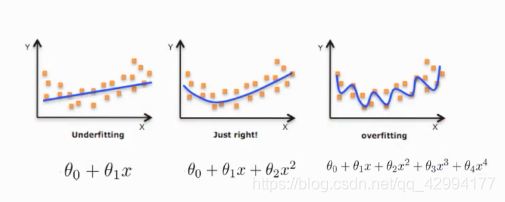
定义
对线性模型进行训练学习会变成复杂模型
现实数据,绝大部分是非线性的,这样最后训练出来的模型就变成了复杂模型。
模型复杂的原因是数据的特征和目标值之间的关系不仅仅是线性关系。
欠拟合原因及解决办法
原因:学习到的数据的过少
解决办法:增加数据的特征数量
过拟合原因及解决办法
交叉验证(让所有数据都有过训练)结合测试结果,可以检验出是否过拟合或欠拟合。
原因:原始特征过多,存在一些嘈杂特征。模型过于复杂是因为模型尝试去兼顾各个测试数据点。
解决办法:
1、进行特征选择,消除关联性大的特征(就是消除特征值是3次方之类的,但是又不能确定哪些特征是3次方)(很难做)
2、正则化(了解)
PS:特征选择分为过滤式和嵌入式。
过滤式:低方差特征
嵌入式:正则化、决策树、神经网络 都有特征选择的概念
回归问题解决过拟合的方式 - 岭回归(带有正则化的线性回归)
线性回归LinearRegression容易出现过拟合。
L2正则化:Ridge岭回归,是带有正则化的线性回归,可以解决过拟合
- L2正则化
正则化 :通过减小特征值的权重,把高次方的特征的权重减小到趋近于0,不断去尝试调整,可以使模型变简单。
岭回归 - 带有正则化的线性回归
API
sklearn.linear_model.Ridge
正则化力度的取值可以通过网格搜索来取一个效果好的值。取值的范围一般在0~1、1~10等。
正则化力度对权重的影响,如下图所示。
正则化力度越大,权重就越趋于0。
案例
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression, SGDRegressor, Ridge
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error
def mylinear():
"""
线性回归直接预测房子价格
:return:
"""
# TODO 获取数据
lb = load_boston()
# TODO 分割数据集到训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)
# TODO 进行标准化处理,目标值处理。
# 特征值和目标值都必须进行标准化处理,实例化两个标准化API
std_x = StandardScaler()
x_train = std_x.fit_transform(x_train)
x_test = std_x.transform(x_test)
# 目标值
std_y = StandardScaler()
y_train = std_y.fit_transform(y_train.reshape(-1,1))
y_test = std_y.transform(y_test.reshape(-1,1))
# sklearn版本若是0.19的,std_y.fit_transform(y_train) 传入的y_train值必须是二维的
# sklearn版本若是0.19的,转换器,estimator(估计器),要求数据必须是二维 .reshape(-1,1)行不确定就填-1,列有一列
# sklearn版本若是0.18的,一维、二维都可以
# TODO estimator预测
# 方法一:正规方程求解方式预测结果
lr = LinearRegression()
lr.fit(x_train, y_train)
print("权重参数(回归系数)为:", lr.coef_)
# 预测测试集的房子价格,inverse_transform 转换为标准化之前的数据
y_lr_predict = lr.predict(x_test)
y_lr_predict = std_y.inverse_transform(y_lr_predict)
print("正规方程测试集中每个房子的预测价格:", y_lr_predict)
print("正规方程的均方误差:", mean_squared_error(std_y.inverse_transform(y_test), y_lr_predict))
# 方法二:梯度下降进行房价预测
sgd = SGDRegressor()
sgd.fit(x_train, y_train)
print("权重参数(回归系数)为:", sgd.coef_)
# 预测测试集的房子价格,inverse_transform 转换为标准化之前的数据
y_sgd_predict = sgd.predict(x_test)
y_sgd_predict = std_y.inverse_transform(y_sgd_predict)
print("梯度下降测试集中每个房子的预测价格:", y_sgd_predict)
print("梯度下降的均方误差:", mean_squared_error(std_y.inverse_transform(y_test), y_sgd_predict))
# 方法三:岭回归进行房价预测
rd = Ridge(alpha=1.0)
rd.fit(x_train, y_train)
print("权重参数(回归系数)为:", rd.coef_)
# 预测测试集的房子价格,inverse_transform 转换为标准化之前的数据
y_rd_predict = rd.predict(x_test)
y_rd_predict = std_y.inverse_transform(y_rd_predict)
print("岭回归测试集中每个房子的预测价格:", y_rd_predict)
print("岭回归的均方误差:", mean_squared_error(std_y.inverse_transform(y_test), y_rd_predict))
return None
if __name__ == '__main__':
mylinear()线性回归LinearRegression与Ridge对比
岭回归:
回归得到的回归系数更符合实际,更可靠。另外,能让估计参数的波动范围变小,变的更稳定。在存在病态数据偏多的研究中有较大的实用价值。