C语言浮点型在内存中的存储
目录
前言:
引言:
浮点数存储规则
举个栗子:
TIP:
单精度浮点数存储的模型(float)
双精度浮点数存储的模型(double)
IEEE对 M 的特殊规定
IEEE对 E 的特殊规定
小试牛刀
先看第一段代码
再看第二段代码
前言:
我们首先需要知道什么是浮点型,以下是两种常见的浮点型。
3.14159 ------------- 这是最常见的浮点型,也就是小数。
1E10 ------------- 这个也表示浮点型,E表示底数10,而E后面的数表示指数,所以E10就是10^10,而E前面的1是数量级,综上,1E10就是1*10^10。
引言:
我们先看一段代码
int main()
{
int n = 9;
float* pFloat = (float*)&n;
printf("n的值为:%d\n", n);
printf("*pFloat的值为:%f\n", *pFloat);
*pFloat = 9.0;
printf("n的值为:%d\n", n);
printf("*pFloat的值为:%f\n", *pFloat);
return 0;
}输出结果:
我们不难发现,当n以整型的方式存进去,然后分别以整型和浮点型的方式取出,发现以浮点型的方式打印结果有问题;对应的,当n以浮点型的方式存进去,再以整型的方式取出,结果也是跟我们想象的不一样。
由此,可以得出一个结论,浮点型在内存中的存储和整型在内存中的存储是不一样的。
浮点数存储规则
根据国际标准IEEE,任意一个二进制浮点数V可以表示成下面的形式:
- (-1)^ S * M * 2 ^ E
- (-1) ^ S表示符号位,当S=0,V是正数,当S=1,V是负数。
- M表示有效数字,大于等于1,小于2
- 2^E表示指数位。
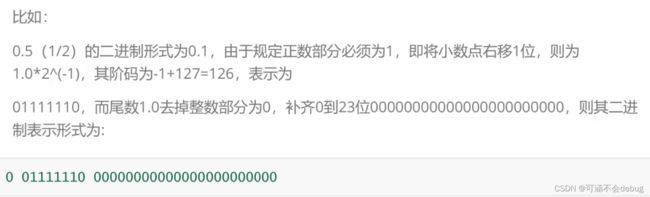
举个栗子:
十进制表示的5.5
首先5的二进制位就是101,而小数部分0.5我们就用1来表示,最终结果就是101.1
为何小数部分用1表示就可以呢?
因为整数部分个位数的权重是2^0,十位数的权重是2^1,百位数的权重是2^2,以此类推,小数部分的第一位表示2^(-1),也就是0.5,小数部分的第二位就是2^(-2)……
因此我们用IEEE表示就是
(-1)^ 0 * 1.011 * 2 ^ 2
所以S=0,M=1.011,E=2
TIP:
理论上任何一个浮点型都可以用IEEE表达形式表示,但如果浮点数过于复杂,就不能精准的表示出来。
比如3.14,小数部分想要表示出0.14,需要我们一直凑,但大概率是凑不出来,会有一些误差!
单精度浮点数存储的模型(float)
对于32位的浮点数,最高的1位是符号位S,接着的8位是指数E,剩下的23位比特位是有效数字M
双精度浮点数存储的模型(double)
对于64位的浮点数,最高的1位是符号位S,接着的11位是指数E,剩下的52位为有效数字M
IEEE对 M 的特殊规定
前面说过,1<=M<2,所以,M可以写成1.xxxxxxxx的形式,其中xxxxxxxxx表示小数部分。
IEEE规定,在计算机内部保存M时,默认这个数的第一位总是1,因此可以被舍去,只保存后面的xxxxxxx小数部分。
比如保存1.01时,只保存01,等到读取的时候,再把第一位的1加上去。这样做的目的是,节省1位有效数字,是的表达小数部分更精确。
IEEE对 E 的特殊规定
首先,E作为一个无符号整数(unsigned int)
这意味着,如果E为8位,它的取值范围是0~255,如果是11位,他的取值范围是0~2047。
但是,我们知道,科学技术法中是可以出现负数的。
所以IEEE规定,存入内存时E的真实值必须加上一个中间数,对于8位的E来说,这个中间数的值就是127,对于11位的E来说,这个中间值就是1023。
我们取出来时,还是需要减去中间数的。
上面讲的内容是讲E如何存储到内存中的,下面开始讲解如何把E取出来。
- E不为全0或不全为1
这是最普遍的情况,我们将指数E的值减去127(或1023),得到真实值,再将有效数字M前加上第一位的1
- E全为0
表示原有的真实值是-127,2^-127是一个非常小的数字,无限接近于0,所以有效数字M不再加上第一位的1,而是还原0.xxxxxxxx的小数,使得接近于0。
- E全为1
表示是2^128次方,是一个非常大的数字,所以表示正负无穷大(正负取决于符号位S)。
小试牛刀
我们现在已经大致掌握了浮点型在内存如何存储和取出,让我们来解决一下引言的问题吧!
int main()
{
int n = 9;
float* pFloat = (float*)&n;
printf("n的值为:%d\n", n);
printf("*pFloat的值为:%f\n", *pFloat);
//分为两段,我们一段一段去解决
*pFloat = 9.0;
printf("n的值为:%d\n", n);
printf("*pFloat的值为:%f\n", *pFloat);
return 0;
}先看第一段代码
9在整型n中的存储形式是
00000000000000000000000000001001
然后我们照搬,将其存储在浮点型
0 00000000 00000000000000000001001
S E M
可以看出E是全0,根据IEEE规定,当E为全0时,我们对于M不需要补数字1,而现在的M也是一个非常小的数字,当我们用%f打印时,只能保留6位有效数字,因此打印结果就是0.000000
再看第二段代码
我们首先是将9.0存储再一个浮点型中
9.0在浮点型中存储的二进制位表达形式是
1001.0
1.001*2^3 (注意一定要表示成科学技术法的形式!再找S、M、E)
S=0 M=1.001(存储在内存就是001) E=3(3+127)
0 10000010 0010000000000000000000
注意M = 001存储直接放在最前面
而将这一部分照搬到整型,发现结果就是一个非常大的数字!1091567616