高级数据结构——红黑树
目录
- 红黑树
-
- 红黑树定义
- 红黑树节点实现
- 红黑树插入实现
- 红黑树删除实现
红黑树
红黑树定义
在之前介绍AVL树时,我们知道AVL树是高度平衡的二叉搜索树,而高度平衡意味着在对AVL树中的节点作更新操作时,我们需要花费较大的时间去动态调整树的结构.而红黑树相当于是对AVL树的一种改善.
红黑树不像AVL树那样保持高度平衡(左右子树的高度差不超过1),而是通过给每个节点添加颜色标志(红/黑)这种限制来保证任意一条路径(从根节点到叶子结点)的长度不会超过其他路径长度的2倍,所以红黑树是一种接近平衡的二叉搜索树.
红黑树具有4个性质
- 每个节点的着色方式只有两种:红色或黑色
- 根节点的着色为黑色
- 如果一个节点的颜色是红色的,那么它的左右子节点(如果存在)其颜色一定是黑色的(即不存在两个连续的红色节点出现)
- 对于每个节点,其从该节点到任意一个叶子结点的路径中黑色节点的个数是相同的
通过红黑树的4个性质我们可以得到对于一棵红黑树而言,最短路径就是全为黑色节点组成的路径,最长节点就是黑红节点交替排列的路径.因此对于含有n个节点的红黑树,其查询的时间复杂度为O(log(n/2))~O(log(n)),因此总的时间复杂度为O(logn)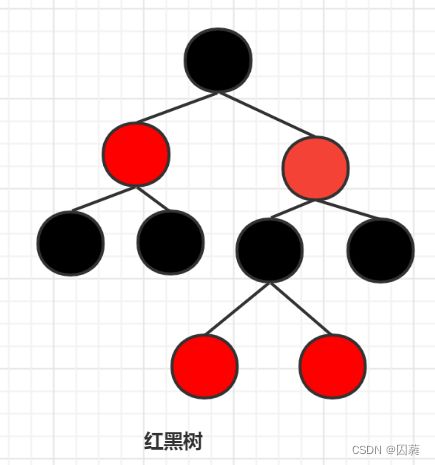
红黑树节点实现
在上面的介绍过程中,我们知道红黑树的每个节点是在二叉搜索树节点的基础上添加了一个颜色标志,因此红黑树的节点实现
static class RBTreeNode{
public int val;
public RBTreeNode left;
public RBTreeNode right;
public RBTreeNode parent;
// COLOR是一个枚举类,其中有两个实例:BLACK,RED
public COLOR color;
public RBTreeNode(int val){
this.val = val;
// 之所以将新插入的节点的颜色默认设置为红色的原因是
// 红黑树要保证任意一条路径上黑色节点的个数相同,而如果设置新插入的节点的颜色是黑色,那么就需要在其他所有路径上添加黑色节点.
this.color = RED;
}
}
public enum COLOR{
BLACK,RED
}
红黑树插入实现
首先我们知道插入的节点的颜色是红色,因此它不会影响插入路径上黑色节点的个数.而当插入节点的父亲节点的颜色为黑色时,此时我们其实无须作任何处理(因为插入的节点是红色唯一可能造成的影响就是两个红色节点相连),如图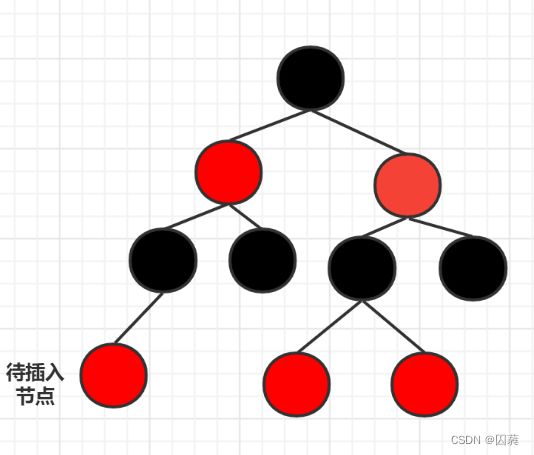
因此我们需要考虑的是待插入节点的父亲节点的颜色为红色.这种情况下待插入节点的爷爷节点一定是黑色,此时我们需要考虑如何将两个连续的红色节点分开且不影响红黑树本身,此时我们需要考虑父亲节点的兄弟节点(叔叔节点)的颜色.
如果叔叔节点的颜色为红色,那么此时只能将父亲节点和叔叔节点的颜色变为黑色,然后爷爷节点的颜色变为红色,然后从爷爷节点开始继续向上遍历调整红黑树的结构.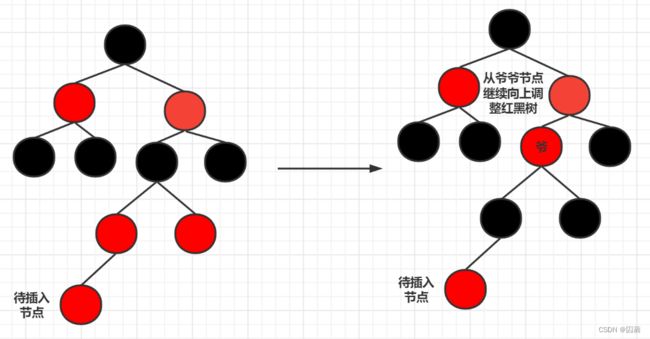
如果叔叔节点的颜色为黑色,那么此时我们只需要通过旋转即可分开连续的两个红色节点,具体的旋转操作请参考高级数据结构——AVL树
此时分为两种情况,第一种情况是待插入节点是父亲节点的左子节点,此时只需右旋爷爷节点,然后交换爷爷节点和父亲节点的颜色
第二种情况是待插入节点是父亲节点的右子节点,此时需要先将第二种情况转化为第一种情况,即左旋父亲节点并交换父亲节点和待插入节点的指针,然后和第一种情况的处理方式类似
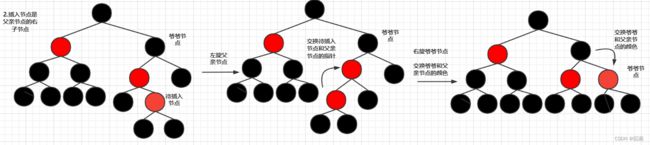
以上讨论的情况是父亲节点是爷爷节点的左子节点,而当父亲节点是爷爷节点的右子节点时,实现逻辑是一致的,就是将左右对调即可.
在对红黑树的结构调整完后,需要注意将根节点的颜色设置为黑色,因为红黑树的结构调整的过程中很有可能会改动到根节点
public class RBTree {
static class RBTreeNode {
public int val;
public RBTreeNode left;
public RBTreeNode right;
public RBTreeNode parent;
public COLOR color;
public RBTreeNode(int val) {
this.val = val;
//默认插入的节点的颜色是红色,如果是黑色会造成插入的麻烦:
//由于要满足任意一条路径上的黑色节点的个数相同,所以要在其他路径上新添加一些没有意义的黑色节点
//而插入的节点是红色节点,我们只需要调节该路径上节点的颜色
this.color = COLOR.RED;
}
}
public RBTreeNode root;
public boolean insert(int val) {
if(root == null){
// 插入第一个节点时直接给根节点赋值即可
root = new RBTreeNode(val);
root.color = COLOR.BLACK;
return true;
}
RBTreeNode node = new RBTreeNode(val);
RBTreeNode cur = root;
RBTreeNode p = null;
// 寻找待插入节点的位置
while (cur != null) {
if (cur.val < val) {
p = cur;
cur = cur.right;
} else if (cur.val == val) {
return false;
} else {
p = cur;
cur = cur.left;
}
}
if (p.val < val) {
p.right = node;
} else if (p.val > val) {
p.left = node;
}
node.parent = p;
cur = node;
// 调整红黑树结构
while (p != null && p.color == COLOR.RED) {
RBTreeNode pp = p.parent;
if (pp.left == p) {
RBTreeNode uncle = pp.right;
// 叔叔节点为红色
if (uncle != null && uncle.color == COLOR.RED) {
p.color = COLOR.BLACK;
uncle.color = COLOR.BLACK;
pp.color = COLOR.RED;
cur = pp;
p = cur.parent;
} else {
// 叔叔节点不存在或为黑色
if (cur == p.right) {
rotateLeft(p);
RBTreeNode tmp = cur;
cur = p;
p = tmp;
}
rotateRight(pp);
pp.color = COLOR.RED;
p.color = COLOR.BLACK;
}
} else {
RBTreeNode uncle = pp.left;
if (uncle != null && uncle.color == COLOR.RED) {
p.color = COLOR.BLACK;
uncle.color = COLOR.BLACK;
pp.color = COLOR.RED;
cur = pp;
p = cur.parent;
} else {
if (cur == p.left) {
rotateRight(p);
RBTreeNode tmp = cur;
cur = p;
p = tmp;
}
rotateLeft(pp);
pp.color = COLOR.RED;
p.color = COLOR.BLACK;
}
}
}
//这个必须加,因为在插入的过程中,红黑树的根是在变化的,而变化则导致根节点的颜色得不到保证
//尤其是遇见第一种青光将pp的颜色设置为红.
root.color = COLOR.BLACK;
return true;
}
private void rotateRight(RBTreeNode p) {
RBTreeNode pp = p.parent;
RBTreeNode newRoot = p.left;
p.left = newRoot.right;
if (p.left != null) {
p.left.parent = p;
}
newRoot.right = p;
p.parent = newRoot;
if (pp != null) {
if (pp.left == p) {
pp.left = newRoot;
newRoot.parent = pp;
} else if (pp.right == p) {
pp.right = newRoot;
newRoot.parent = pp;
}
} else {
newRoot.parent = null;
root = newRoot;
}
}
private void rotateLeft(RBTreeNode p) {
RBTreeNode pp = p.parent;
RBTreeNode subR = p.right;
RBTreeNode subRL = subR.left;
p.right = subRL;
if (subRL != null) {
subRL.parent = p;
}
subR.left = p;
p.parent = subR;
if (pp != null) {
if (pp.left == p) {
pp.left = subR;
subR.parent = pp;
} else if (pp.right == p) {
pp.right = subR;
subR.parent = pp;
}
} else {
subR.parent = null;
root = subR;
}
}
红黑树删除实现
红黑树的删除的主要思路和二叉搜索树的删除思路相似,都是先找到待删除的节点,然后通过找该节点的前驱节点或后继节点来找到替罪羊节点,然后删除替罪羊节点,将替罪羊节点的值赋给待删除节点.
因此我们主要关心的是删除红黑树的叶子节点时会对红黑树的结构造成什么影响.首先如果删除的叶子节点是红色,那么很显然直接删除掉即可,因为红色节点的去除不会影响该路径下黑色节点的个数.如图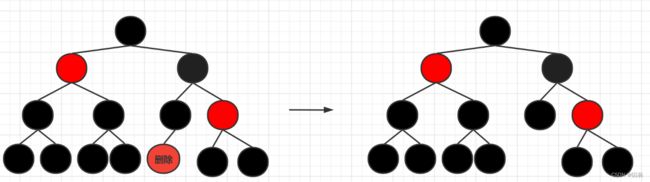
而要删除的叶子节点是黑色时,由于该路径下黑色节点的个数减少,所以需要对红黑树进行调整.
首先我们要考虑的是尽可能的减少调整红黑树的结构,因此我们首先应该调整的是以待删除节点的父亲节点为根节点的子树的结构.首先规定待删除节点的父亲为父亲节点,其相邻兄弟节点为兄弟节点,兄弟的孩子节点为侄子节点,以父亲节点为根节点的子树称为p树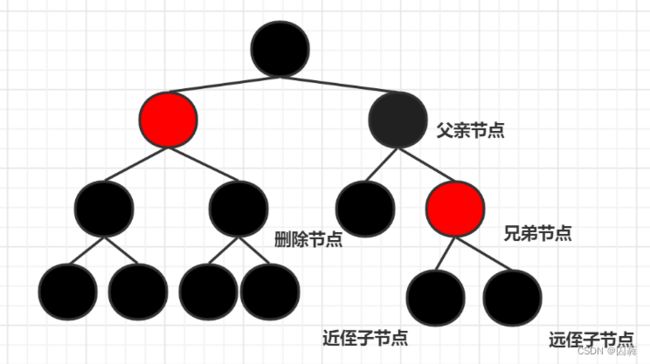
p树的节点情况大致可以分为5种
-
父亲节点为红色节点,兄弟节点和侄子节点为黑色节点(或为null)
这种情况下删除节点后删除节点所在路径上黑色节点个数-1,因此我们可以将父亲节点和兄弟节点的颜色对换.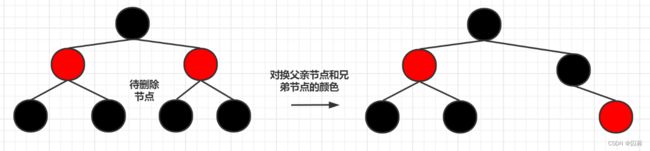
-
父亲节点,兄弟节点和侄子节点均为黑色(或为null)
这种情况下只需要将兄弟节点的颜色置位红色即可,然后p树的所有路径下黑色节点个数均少1个,因此以父亲节点为基础向上继续调整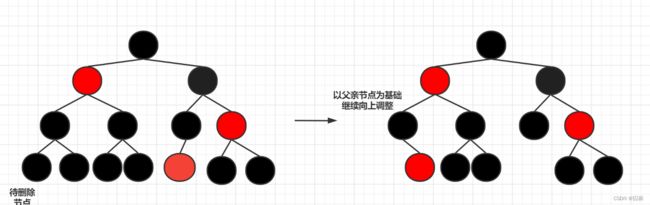
-
兄弟节点为红色
这种情况下父亲节点和侄子节点的颜色均为黑色(不允许两个连续的红色节点出现).此时删除节点后,该路径下黑色节点个数-1,此时我们将p树左旋,并交换父亲节点和兄弟节点的颜色,此时p树就变成了第1种情况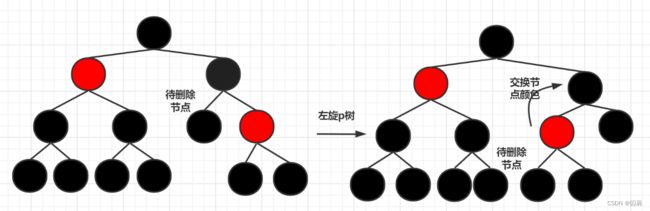
-
兄弟节点为黑色,远侄子节点为红色
此时我们可以想到将远侄子节点移动到待删除一侧的路径上并置为黑色.所以首先左旋p树,将父亲节点和兄弟节点颜色对换,然后将远侄子节点的颜色置位黑色
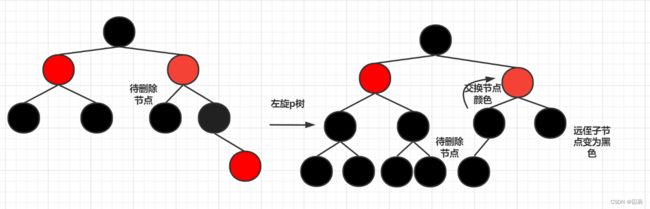
-
兄弟节点为黑色,近侄子节点为红色,远侄子节点为黑色
这种情况和第4种情况类似,因此我们考虑先将第5种情况转换成第4种情况,然后按照第4种情况进行处理.所以首先对兄弟节点右旋,然后交换兄弟节点和近侄子节点的颜色变成第4种情况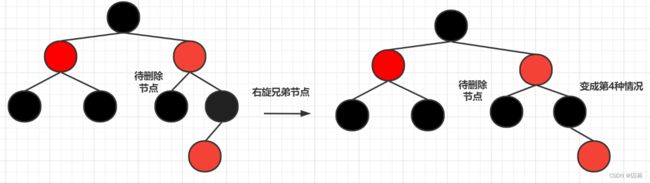
综上我们已经讨论了删除节点为父亲节点的左子节点时的所有情况,而当删除节点为父亲节点的右子节点时,只需要将left和right对调即可
和二叉搜索树的删除节点一样,我们首先需要找到替罪羊节点,然后将替罪羊节点的值赋给待删除节点.(寻找替罪羊节点可以参考高级数据结构——AVL树)然后以替罪羊节点为待删除节点进行红黑树结构的调整.
public int remove(int val){
RBTreeNode replaced = getNode(val);
if(replaced == null){
throw new RuntimeException("没有要删除的节点");
}
RBTreeNode removed = replaced;
if(removed.left != null && removed.right != null){
removed = getNextNode(removed);
}
RBTreeNode moved;
RBTreeNode parent = removed.parent;
if(removed.left != null){
moved = removed.left;
}else{
moved = removed.right;
}
if(moved != null){
moved.parent = parent;
}
if(parent.left == removed){
parent.left = moved;
}else{
parent.right = moved;
}
int oldVal = replaced.val;
if(removed.val != replaced.val){
replaced.val = removed.val;
}
adjustStructure(parent,moved,removed.color);
root.color = COLOR.BLACK;
return replaced.val;
}
private void adjustStructure(RBTreeNode parent,RBTreeNode removed,COLOR color){
RBTreeNode uncle;
do {
if(parent.left == removed){
if(color == COLOR.BLACK){
uncle = parent.right;
RBTreeNode near = null;
RBTreeNode far = null;
if(uncle != null){
near = uncle.left;
far = uncle.right;
}
if (parent.color == COLOR.RED && (first(uncle)) && first(near) && first(far)) {
// 1.父亲为红,兄弟和侄子为黑
if(uncle != null) {
uncle.color = COLOR.RED;
}
parent.color = COLOR.BLACK;
break;
} else if (first(parent) && first(uncle) && first(near) && first(far)) {
// 2.父亲,兄弟和侄子都为黑色
if(uncle != null){
uncle.color = COLOR.RED;
}
removed = parent;
parent = removed.parent;
} else if (uncle != null && uncle.color == COLOR.RED) {
// 3.兄弟为红色
rotateLeft(parent);
COLOR color1 = parent.color;
parent.color = uncle.color;
uncle.color = color1;
// 变成第一种情况
} else if (uncle != null && uncle.color == COLOR.BLACK && far != null && far.color == COLOR.RED) {
// 4.兄弟为黑色,远侄子为红色
rotateLeft(parent);
COLOR color1 = parent.color;
parent.color = uncle.color;
uncle.color = color1;
far.color = COLOR.BLACK;
break;
} else if (uncle != null && uncle.color == COLOR.BLACK
&& near != null && near.color == COLOR.RED
&& (far == null || far.color == COLOR.BLACK)) {
// 5.兄弟为黑色,近侄子为红色,远侄子为黑色
rotateRight(uncle);
uncle.color = COLOR.RED;
near.color = COLOR.BLACK;
rotateLeft(parent);
COLOR color1 = parent.color;
parent.color = uncle.color;
uncle.color = color1;
near.color = COLOR.BLACK;
break;
}
}
}else{
if(color == COLOR.BLACK){
while(parent != null) {
uncle = parent.left;
RBTreeNode near = null;
RBTreeNode far = null;
if(uncle != null){
near = uncle.right;
far = uncle.left;
}
if (parent.color == COLOR.RED && (first(uncle)) && first(near) && first(far)) {
// 1.父亲为红,兄弟和侄子为黑
if(uncle != null) {
uncle.color = COLOR.RED;
}
parent.color = COLOR.BLACK;
break;
} else if (first(parent) && first(uncle) && first(near) && first(far)) {
// 2.父亲,兄弟和侄子都为黑色
if(uncle != null){
uncle.color = COLOR.RED;
}
removed = parent;
parent = removed.parent;
} else if (uncle != null && uncle.color == COLOR.RED) {
// 3.兄弟为红色
rotateRight(parent);
COLOR color1 = parent.color;
parent.color = uncle.color;
uncle.color = color1;
// 变成第一种情况
} else if (uncle != null && uncle.color == COLOR.BLACK && far != null && far.color == COLOR.RED) {
// 4.兄弟为黑色,远侄子为红色
rotateRight(parent);
COLOR color1 = parent.color;
parent.color = uncle.color;
uncle.color = color1;
far.color = COLOR.BLACK;
break;
} else if (uncle != null && uncle.color == COLOR.BLACK
&& near != null && near.color == COLOR.RED
&& (far == null || far.color == COLOR.BLACK)) {
// 5.兄弟为黑色,近侄子为红色,远侄子为黑色
rotateLeft(uncle);
rotateRight(parent);
COLOR color1 = parent.color;
parent.color = uncle.color;
uncle.color = color1;
near.color = COLOR.BLACK;
break;
}
}
}
}
}while(parent != null);
}
private boolean first(RBTreeNode node){
return node == null || node.color == COLOR.BLACK;
}
private RBTreeNode getNode(int val){
if(root == null){
return null;
}
RBTreeNode cur = root;
while(cur.val != val){
if(cur.val < val){
cur = cur.right;
}else if(cur.val > val){
cur = cur.left;
}
}
return cur;
}
private RBTreeNode getNextNode(RBTreeNode node){
if(node == null || root == null){
return null;
}
RBTreeNode cur = node;
if(node.right != null){
node = node.right;
while(node.left != null){
node = node.left;
}
return node;
}else{
RBTreeNode parent = cur.parent;
while(parent != null && parent.right == cur){
cur = parent;
parent = cur.parent;
}
return parent;
}
}