数据结构算法与应用-C++语言描述 stack的应用
//数据结构算法与应用-C++语言描述 stack链表的实现
//链表描述
#include ::trimToSize,它使数组的长度等于 max{listSize,1}。
//这个方法的复杂度是多少?” 测试你的代码。
arrayList<T>& trimToSize();
//ex6. 编写方法 arrayList::setSize,它使线性表的大小等于指定的大小。若线性表开始的大小
//小于指定的大小,则不增加元素。若线性表开始的大小大于指定的大小,则删除多余的元
//素。这个方法的复杂度是多少? 测试你的代码。
arrayList<T>& setSize(int length);
//ex7. 重载操作符[],使得表达式 x加返回对线性表第i个元素的引用。
//若线性表没有第i个元则抛出异常语句 x[i]=y 和 y= x[i]] 按以往预期的方式执行。
//测试你的代码。
T& operator[](int i);
//ex8. 重载操作符 ==,使得表达式 x==y 返回 true,当上且仅当两个用数组描述的线性表x
//和y 相等(即对所有的 i,两个线性表的第i 个元素相等 )。测试你的代码。
bool operator==(const arrayList<T>& right) const;
//ex9.
bool operator!=(const arrayList<T>& right) const;
//ex10. 重载操作符 <,使得表达式 x
//于用数组描述的线性表v ( 见练习 8 )。测试你的代码。
bool operator<(const arrayList<T>& right) const;
//ex11. 编写方法 arrayList::push_back,它把元素 theElement 插到线性表的右端。不要利用
//insert 方法。方法的时间复杂度是多少?测试你的代码。
void push_back(const T& theElement);
//ex12. 编写方法 arrayList::pop_back,它把线性表右端的元素删除。不要利用 erase 方法。方
//法的时间复杂度是多少? 测试你的代码。
T& pop_back();
//ex13. 编写方法 arrayList::swap(theLisb,它交换线性表的元素 *this 和 theList。方法的时间
//复杂度是多少? 测试你的代码。
arrayList<T>& swap(arrayList<T>& theList);
//ex14. 编写方法 arrayList::reserve(theCapacity),它把数组的容量改变为当前容量和 theCapacity
//的较大者。测试你的代码。
arrayList<T>& reserve(int theCapacity);
//ex15. 编写方法 arrayList::set(theIndex,theElement),它用元素 theElement 替换索引为 theIndex
//的元素。若索引 theIndex 超出范围,则抛出异常。返回原来索引为 theIndex 的元素。测试
//你的代码。
T set(int theIndex, const T& theElement);
//ex16. 编写方法 arrayList::clear,它使线性表为空。方法的复杂度是多少?” 测试你的代码。
arrayList<T>& clear();
//ex17. 编写方法 arrayList::removeRange,它删除指定索引范围内的所有元素。方法的复杂度
//是多少?测试你的代码。
arrayList<T>& removeRange(int startIndex,int endIndex);
//ex18. 编写方法 arrayList::lastInexOf,它的返回值是指定元素最后出现时的索引。如果这样
//的元素不存在,则返回 -1。方法的复杂度是多少? 测试你的代码。
int lastIndexOf(const T& theElement) const;
//ex20. 类 arrayList ( 程序 5-1 ) 的缺点是,它不减少数组 element 的长度。
//1: 编写类 arrayList 的一个新版本。如果在删除之后,线性表的大小降至 arrayLength/4 以
// 下,就创建一个新的数组,长度为 max{arrayLength/2,initialCapacity}。然后将老表
// 中的元素复制到新表。
//2 ( 选择性练习 ) 从空表开始,考察大小为地的线性表的操作序列。假设当初始容量等于
// 或超过线性表大小的最大值时,总的执行步数是f(n)。证明,如果起始容量为1,而且
// 在插入和删除操作中,可以按照上面和 5.3 节所述的方式改变数组长度,那么执行步
// 数最多为 cf(n),其中 c 是某个常数。
arrayList<T>& decreaseArray(int capacity);
///ex33. 1 ) 编写方法 arrayList::reverse,它原地颠倒线性表元素的顺序 ( 即在数组 element 中
// 完成操作,不创建新的数组 )。颠倒顺序之前,线性表的第 k 个元素是 element[k],站
// 倒之后,线性表的第 k 个元素是 element[listSize-k-1]。不要利用 STL 函数 reverse。
// 2 ) 方法应具有 listSize 的线性复杂度。证明这个性能。
// 3 ) 设计测试数据,测试方法的正确性。
// 4 ) 编写另一个原地颠倒 arrayList 对象的方法。它不是 arrayList 的成员函数,不能访问
// arrayList 的数据成员。不过,这个方法可以调用 arrayList 的成员函数。
// 5 ) 计算方法的复杂度
// 6 ) 使用大小分别为 1000、5000 和 10 000 的线性表,比较两个颠倒顺序算法的运行时间
arrayList<T>& reverse();
//ex23.1) 编写方法 arrayList::leftShift(i),它将线性表的元素向左移动i个位置。如果
// x=[0,1,2,3,4],那么 x.leftShift(2) 的结果是 x=[2,3,4]。
// 2 ) 计算方法的复杂度。
// 3 ) 测试你的代码-
arrayList<T>& leftShift(int shift);
//ex24. 在一个循环移动的操作中,线性表的元素根据给定的值,按顺时针方向移动。例如,
//x=[0,1,2,3,4],循环移动 2 的结果是 x=[2,3,4,0,1]。
// 1 ) 描述一下如何利用 3 次逆转操作完成循环移动。每一次逆转操作都可以将线性表的一
// 部分或全部逆转。
// 2 ) 编写方法 arrayList::circularShiftt),它将线性表的元素循环移动i个位置。方法应
// 具有线性表长度的线性复杂度。
// 3 ) 测试你的代码。
arrayList<T>& circularShift(int shift);
//ex25. 调用语句 x.half,可以将 x 的元素隔一个删除一个。如果 xsize() 是 7, xelement[]=[2,13,4.5,17,8,29],
// 那么 x.half() 的结果是 x.size() 是 4,x.element[]=[2,4.17,9]。如果 x.size() 是 4,x.element[]=[2,13,4.5],
// 那么 x.half() 的结果是 x.size() 是 2,x.element[]=[2,4]。如果 x 为空,那么 x.half() 的结果也是X 为空。
// 1 ) 编写方法 arrayList::half()。不能利用类 arrayList 的其他方法。复杂度应该为O(listSize)
// 2 ) 证明方法的复杂度为 O(listSize)。
// 3 ) 测试你的代码。
arrayList<T>& half();
///ex34.令 a 和b 是类 arrayList 的两个对象。
// 1 ) 编写方法 arrayList::meld(ab),它生成一个新的线性表,从 a 的第 0 个元素开始,
// 交替地包含a 和 b的元素。如果一个表的元素取完了,就把另一个表的剩余元素附加
// 到新表中。调用语句 c.meld(a,b) 使 成为合并后的表。方法应具有两个输入线性表大
// 小的线性复杂度。
// 2 ) 证明方法具有 a 和b 大小之和的线性复杂度。
// 3 ) 测试你的代码。
arrayList<T>& meld(arrayList<T>& a, arrayList<T>& b);
///ex35.令a 和b 是类 arrayList 的两个对象。假设它们的元素从左到右非递减有序。
// 1 ) 编写方法 arrayList::merge(a,b),它生成一个新的有序线性表,包含a 和 的所有元
// 素。归并后的线性表是调用对象 *this。不要利用 STL 本数 merge。
// 2 ) 计算方法的复杂度。
// 3 ) 测试你的代码。
arrayList<T>& merge(arrayList<T>& a, arrayList<T>& b);
///ex36. 1 ) 编写方法 arrayList::split(lab),它生成两个线性表a 和b。a 包含 *this 中索引为偶
// 数的元素,b 包含其余的元素。
// 2 ) 计算方法的复杂度。
// 3 ) 测试你的代码。
arrayList<T>& split(arrayList<T>& a, arrayList<T>& b);
//ex31. 假设用公式 ( 5-3 ) 来表示线性表。分别用变量 first 和 last 表示线性表首元素和尾元素的
// 位置。
// 1 ) 开发一个类 circularArrayList,它与 arrayList 类似。实现所有的方法。在删除和插人方
// 法中,对位于删除或插和人元素的左面或右面的元素,有选择地决定向左移动或向右移
// 动,以此提高方法的性能。
// 2 ) 计算每一个方法的复杂度。
// 3 ) 测试你的代码。
public:
class iterator
{
public:
// C++ 的typedef 语句实现双向迁代器
typedef bidirectional_iterator_tag iterator_category;
typedef T value_type;
typedef ptrdiff_t difference_type;
typedef T* pointer;
typedef T& reference;
//构造函数
iterator(T* thePosition = 0){ position = thePosition; }
//解引用操作符
T& operator*() const{ return *position; }
T* operator->() const{ return &*position; }
//迭代器的值增加
iterator& operator++() //前加
{
++position;
return *this;
}
iterator operator++(int) //后加
{
iterator old = *this;
++position;
return old;
}
//迭代器的值减少
iterator& operator--() //前减
{
--position;
return *this;
}
iterator operator--(int) //后减
{
iterator old = *this;
--position;
return old;
}
//测试是否相等
bool operator!=(const iterator right) const
{
return position != right.position;
}
bool operator==(const iterator right) const
{
return position == right.position;
}
//27. 扩展迭代器类 arrayList::iterator ( 程序 5-11 ),使得它成为随机访问迭代器。利用 STL 的
// 排序函数对一个线性表排序,以测试这个和迭代器类。
T& operator[](int i)
{
return *(position + i);
}
ptrdiff_t operator-(const arrayList<T>::iterator & right) const
{
return position - right.position;
}
T& operator-(const ptrdiff_t & diff) const
{
return *(position - diff);
}
T& operator+(const ptrdiff_t & diff) const
{
return *(position + diff);
}
protected:
T* position; //指向表元素的指针
};
iterator begin(){ return iterator(element); }
iterator end(){ return iterator(element+listSize); }
protected:
//索引 theIndex 无效,则抛出异常
void checkIndex(int theIndex) const;
//扩容
void increaseArray(int capacity);
//存储线性表元素的一维数组
T* element = NULL;
//一维数组的容量
int arrayLength = 0;
//线性表的元素个数
int listSize = 0;
//初始容量
int initialCapacity = 10;
};
//类 arrayList 的构造函数
template<class T>
arrayList<T>::arrayList(int initialCapacity)
{
//构造函数
if(initialCapacity < 1)
{
ostringstream s;
s<<"Initial capacity = "<<initialCapacity<<" must be > 0";
throw logic_error(s.str());
}
arrayLength = initialCapacity;
initialCapacity = initialCapacity;
element = new T[arrayLength];
listSize = 0;
}
template<class T>
arrayList<T>::arrayList(const arrayList<T>& theList)
{
//复制构造函数
arrayLength = theList.arrayLength;
listSize = theList.listSize;
element = new T[arrayLength];
//利用了 STL 的算法copy
copy(theList.element,theList.element + listSize,element);
}
//方法 checkIndex的时间复杂度是 (1),
template<class T>
void arrayList<T>::checkIndex(int theIndex) const
{
//确定索引theIndex在0 和 listSize - 1之间
if(theIndex < 0 || theIndex >= listSize)
{
//字符串输出流对象
ostringstream s;
s<<"index = "<<theIndex<<" size = "<<listSize;
throw logic_error(s.str());
}
}
//方法 get的时间复杂度是 (1),
template<class T>
T& arrayList<T>::get(int theIndex) const
{
//返回索引为 theIndex 的元素
//若此元素不存在,则抛出异常
checkIndex(theIndex);
return element[theIndex];
}
//indexOf 的时间复杂度是 O(max{listSize,1})
template<class T>
int arrayList<T>::indexOf(const T& theElement) const
{
//返回元素 theElement 第一次出现时的索引
//该元素不存在,则返回 -1
//查找元素 theElement
int theIndex = (int)(find(element,element+listSize,theElement) - element);
//确定元素 theElement 是否找到
if(theIndex == listSize)
{
//没有找到
return -1;
}
else
{
return theIndex;
}
}
/*
删除一个元素为了从线性表中删除索引为 theIndex 的元素,
首先要确定线性表包含这个元素,然后删除这个元素。
若没有这个元素,则抛出类型为异常
如果没有索引 theIndex 的元素,
就抛出异常,erase 时间复杂度是 O(1)。如果有这个元素,
那么要移动的元素个数是 listSize-theIndex
时间复杂度是 O(listSize-theIndex)
*/
template<class T>
void arrayList<T>::erase(int theIndex)
{
//删除其索引为 theIndex 的元素
//如果该元素不存在,则抛出异常
checkIndex(theIndex);
//有效索引,移动其索引大于 theIndex 的元素
copy(element+theIndex+1,element+listSize,element+theIndex);
//调用析构函数
element[--listSize].~T();
}
/*
插入一个元素
要在线性表中索引为 theIndex 的位置上插和人一个新元素,
首先把索引从 theIndex 到listSize-1的元素向右移动一个位置
然后将新元素插人索引为 theIndex 的位置最后将变量listSize 的值增 1。
向右移动元素的操作是利用 STL 函数 copy_backward 来完成的
而没有利用 copy 函数该函数是从最右端的元素开始移动。
*/
template<class T>
void arrayList<T>::insert(int theIndex,const T& theElement)
{
//在索引 theIndex 处插入元素 theElement
//确定索引theIndex在0 和 listSize 之间
if(theIndex < 0 || theIndex > listSize)
{
//字符串输出流对象
ostringstream s;
s<<"index = "<<theIndex<<" size = "<<listSize;
throw logic_error(s.str());
}
//有效索引,确定数组是否已满
if(listSize == arrayLength)
{
//数组空间已满,数组长度倍增
changeLength1D(element,arrayLength,2*arrayLength);
arrayLength *= 2;
}
//把元素向右移动一个位置
copy_backward(element + theIndex,
element + listSize,
element + listSize + 1);
element[theIndex] = theElement;
listSize++;
}
//输出函数 output 和重载 <<
template<class T>
void arrayList<T>::output(ostream& out) const
{
//把线性表插入输出流
copy(element, element + listSize,ostream_iterator<T>(cout," "));
}
//重载 <<
template<class T>
ostream& operator<<(ostream& out,const arrayList<T>& x)
{
x.output(out);
return out;
}
//扩容
template<class T>
void arrayList<T>::increaseArray(int capacity)
{
if(capacity <= arrayLength)
{
cout<<"input capacity <= arrayLength";
return;
}
changeLength1D(element,arrayLength,capacity);
arrayLength = capacity;
}
//ex5. 编写一个方法 arrayList::trimToSize,它使数组的长度等于 max{listSize,1}。
//这个方法的复杂度是多少?” 测试你的代码。
template<class T>
arrayList<T>& arrayList<T>::trimToSize()
{
if(listSize == arrayLength) return *this;
int oldLength = arrayLength;
arrayLength = max(listSize,1);
changeLength1D(element,oldLength,arrayLength);
return *this;
}
//ex6. 编写方法 arrayList::setSize,它使线性表的大小等于指定的大小。若线性表开始的大小
//小于指定的大小,则不增加元素。若线性表开始的大小大于指定的大小,则删除多余的元
//素。这个方法的复杂度是多少? 测试你的代码。
template<class T>
arrayList<T>& arrayList<T>::setSize(int length)
{
if(length < 0 || length > listSize)
return *this;
listSize = length;
return *this;
}
//ex7. 重载操作符[],使得表达式 x加返回对线性表第i个元素的引用。
//若线性表没有第i个元则抛出异常语句 x[i]=y 和 y= x[i] 按以往预期的方式执行。
//测试你的代码。
template<class T>
T& arrayList<T>::operator[](int i)
{
checkIndex(i);
return element[i];
}
//ex8. 重载操作符 ==,使得表达式 x==y 返回 true,当上且仅当两个用数组描述的线性表x
//和y 相等(即对所有的 i,两个线性表的第i 个元素相等 )。测试你的代码。
template<class T>
bool arrayList<T>::operator==(const arrayList<T>& right) const
{
if(right.listSize != listSize) return false;
for(int i = 0;i < listSize;i++)
{
if(element[i] != right.element[i]) return false;
}
return true;
}
//ex9.
template<class T>
bool arrayList<T>::operator!=(const arrayList<T>& right) const
{
if(*this == right)
{
return false;
}
else
{
return true;
}
}
//ex10. 重载操作符 <,使得表达式 x
//于用数组描述的线性表v ( 见练习 8 )。测试你的代码。
template<class T>
bool arrayList<T>::operator<(const arrayList<T>& right) const
{
int minSize = min(size(),right.size());
for(int i = 0;i<size();i++)
{
if(element[i] < right.element[i]) return true;
}
if(size() < right.size()) return true;
return false;
}
//ex11. 编写方法 arrayList::push_back,它把元素 theElement 插到线性表的右端。不要利用
//insert 方法。方法的时间复杂度是多少?测试你的代码。
template<class T>
void arrayList<T>::push_back(const T& theElement)
{
if(arrayLength == listSize)
increaseArray(2*arrayLength);
element[listSize++] = theElement;
}
//ex12. 编写方法 arrayList::pop_back,它把线性表右端的元素删除。不要利用 erase 方法。方
//法的时间复杂度是多少? 测试你的代码。
template<class T>
T& arrayList<T>::pop_back()
{
if(listSize == 0)
{
throw logic_error("arrayList is empty");
}
T& theElement = element[--listSize];
if(listSize < arrayLength/4)
decreaseArray(arrayLength/2);
return theElement;
}
//ex13. 编写方法 arrayList::swap(theLisb,它交换线性表的元素 *this 和 theList。方法的时间
//复杂度是多少? 测试你的代码。
template<class T>
arrayList<T>& arrayList<T>::swap(arrayList<T>& theList)
{
std::swap(listSize, theList.listSize);
std::swap(arrayLength,theList.arrayLength);
std::swap(element,theList.element);
return *this;
}
//ex14. 编写方法 arrayList::reserve(theCapacity),它把数组的容量改变为当前容量和 theCapacity
//的较大者。测试你的代码。
template<class T>
arrayList<T>& arrayList<T>::reserve(int theCapacity)
{
if(theCapacity <= arrayLength) return *this;
changeLength1D(element,arrayLength,theCapacity);
arrayLength = theCapacity;
return *this;
}
//ex15. 编写方法 arrayList::set(theIndex,theElement),它用元素 theElement 替换索引为 theIndex
//的元素。若索引 theIndex 超出范围,则抛出异常。返回原来索引为 theIndex 的元素。测试
//你的代码。
template<class T>
T arrayList<T>::set(int theIndex, const T& theElement)
{
checkIndex(theIndex);
T tmp = element[theIndex];
element[theIndex] = theElement;
return tmp;
}
//ex16. 编写方法 arrayList::clear,它使线性表为空。方法的复杂度是多少?” 测试你的代码。
template<class T>
arrayList<T>& arrayList<T>::clear()
{
for(int i = 0; i < size(); i++)
{
element[i].~T();
}
listSize = 0;
decreaseArray(initialCapacity);
arrayLength = initialCapacity;
return *this;
}
//ex17. 编写方法 arrayList::removeRange,它删除指定索引范围内的所有元素。方法的复杂度
//是多少?测试你的代码。
template<class T>
arrayList<T>& arrayList<T>::removeRange(int startIndex,int endIndex)
{
checkIndex(startIndex);
checkIndex(endIndex);
int count = endIndex - startIndex + 1;
copy(element+endIndex, element+listSize, element+startIndex);
for(int i = startIndex+count;i<listSize;i++)
element[i].~T();
listSize -= count;
if(listSize < arrayLength/4)
{
decreaseArray(arrayLength/2);
}
return *this;
}
//ex18. 编写方法 arrayList::lastInexOf,它的返回值是指定元素最后出现时的索引。如果这样
//的元素不存在,则返回 -1。方法的复杂度是多少? 测试你的代码。
template<class T>
int arrayList<T>::lastIndexOf(const T& theElement) const
{
for(int i = listSize - 1;i>=0;i--)
{
if(element[i] == theElement)
return i;
}
return -1;
}
//ex20. 类 arrayList ( 程序 5-1 ) 的缺点是,它不减少数组 element 的长度。
//1: 编写类 arrayList 的一个新版本。如果在删除之后,线性表的大小降至 arrayLength/4 以
// 下,就创建一个新的数组,长度为 max{arrayLength/2,initialCapacity}。然后将老表
// 中的元素复制到新表。
//2 ( 选择性练习 ) 从空表开始,考察大小为地的线性表的操作序列。假设当初始容量等于
// 或超过线性表大小的最大值时,总的执行步数是f(n)。证明,如果起始容量为1,而且
// 在插入和删除操作中,可以按照上面和 5.3 节所述的方式改变数组长度,那么执行步
// 数最多为 cf(n),其中 c 是某个常数。
template<class T>
arrayList<T>& arrayList<T>::decreaseArray(int capacity)
{
if(capacity >= arrayLength || capacity < 0)
{
return *this;
}
changeLength1D(element, arrayLength, capacity);
arrayLength = capacity;
return *this;
}
///ex33. 1 ) 编写方法 arrayList::reverse,它原地颠倒线性表元素的顺序 ( 即在数组 element 中
// 完成操作,不创建新的数组 )。颠倒顺序之前,线性表的第 k 个元素是 element[k],站
// 倒之后,线性表的第 k 个元素是 element[listSize-k-1]。不要利用 STL 函数 reverse。
// 2 ) 方法应具有 listSize 的线性复杂度。证明这个性能。
// 3 ) 设计测试数据,测试方法的正确性。
// 4 ) 编写另一个原地颠倒 arrayList 对象的方法。它不是 arrayList 的成员函数,不能访问
// arrayList 的数据成员。不过,这个方法可以调用 arrayList 的成员函数。
// 5 ) 计算方法的复杂度
// 6 ) 使用大小分别为 1000、5000 和 10 000 的线性表,比较两个颠倒顺序算法的运行时间
template<class T>
arrayList<T>& arrayList<T>::reverse()
{
for(int i = 0;i < listSize / 2; i++)
{
std::swap(element[i],element[listSize - i - 1]);
}
return *this;
}
//ex23.1) 编写方法 arrayList::leftShift(i),它将线性表的元素向左移动i个位置。如果
// x=[0,1,2,3,4],那么 x.leftShift(2) 的结果是 x=[2,3,4]。
// 2 ) 计算方法的复杂度。
// 3 ) 测试你的代码-
template<class T>
arrayList<T>& arrayList<T>::leftShift(int shift)
{
if(shift < 0 || shift > listSize)
{
ostringstream s;
s << "shift shift < 0 || shift > listSize";
throw logic_error(s.str());
}
copy(element + shift,element + listSize, element);
listSize -= shift;
for (int i = listSize - shift; i < listSize; i++)
{
element[i].~T();
}
if (listSize < arrayLength / 4)
{
changeLength1D(element, arrayLength, arrayLength / 2);
}
return *this;
}
//ex24. 在一个循环移动的操作中,线性表的元素根据给定的值,按顺时针方向移动。例如,
//x=[0,1,2,3,4],循环移动 2 的结果是 x=[2,3,4,0,1]。
// 1 ) 描述一下如何利用 3 次逆转操作完成循环移动。每一次逆转操作都可以将线性表的一
// 部分或全部逆转。
// 2 ) 编写方法 arrayList::circularShiftt),它将线性表的元素循环移动i个位置。方法应
// 具有线性表长度的线性复杂度。
// 3 ) 测试你的代码。
template<class T>
arrayList<T>& arrayList<T>::circularShift(int shift)
{
if(shift < 0)
{
ostringstream s;
s <<"circularShift shift < 0";
throw logic_error(s.str());
}
shift %= listSize;
reverse();
std::reverse(element, element + listSize - shift);
std::reverse(element + listSize - shift, element + listSize);
return *this;
}
//ex25. 调用语句 x.half,可以将 x 的元素隔一个删除一个。如果 xsize() 是 7, xelement[]=[2,13,4.5,17,8,29],
// 那么 x.half() 的结果是 x.size() 是 4,x.element[]=[2,4.17,9]。如果 x.size() 是 4,x.element[]=[2,13,4.5],
// 那么 x.half() 的结果是 x.size() 是 2,x.element[]=[2,4]。如果 x 为空,那么 x.half() 的结果也是X 为空。
// 1 ) 编写方法 arrayList::half()。不能利用类 arrayList 的其他方法。复杂度应该为O(listSize)
// 2 ) 证明方法的复杂度为 O(listSize)。
// 3 ) 测试你的代码。
template<class T>
arrayList<T>& arrayList<T>::half()
{
if(listSize <= 1) return *this;
for(int i = 1;i < (listSize + 1) / 2; i++)
{
element[i] = element[i*2];
}
int oldSize = listSize;
listSize = (listSize + 1) / 2;
for(int i = listSize; i < oldSize; i++)
{
element[i].~T();
}
if(listSize < arrayLength / 4)
{
changeLength1D(element, arrayLength, arrayLength / 2);
}
return *this;
}
///ex34.令 a 和b 是类 arrayList 的两个对象。
// 1 ) 编写方法 arrayList::meld(ab),它生成一个新的线性表,从 a 的第 0 个元素开始,
// 交替地包含a 和 b的元素。如果一个表的元素取完了,就把另一个表的剩余元素附加
// 到新表中。调用语句 c.meld(a,b) 使 成为合并后的表。方法应具有两个输入线性表大
// 小的线性复杂度。
// 2 ) 证明方法具有 a 和b 大小之和的线性复杂度。
// 3 ) 测试你的代码。
template<class T>
arrayList<T>& arrayList<T>::meld(arrayList<T>& a, arrayList<T>& b)
{
if(a.listSize == 0 && b.listSize == 0) return *this;
int minSize = a.listSize < b.listSize ? a.listSize:b.listSize;
int maxSize = a.listSize > b.listSize ? a.listSize:b.listSize;
int newLength = a.listSize > b.listSize ? a.arrayLength : b.arrayLength;
T* maxElement = a.listSize > b.listSize ? a.element:b.element;
if(maxSize + minSize > arrayLength)
{
newLength = a.arrayLength + b.arrayLength;
}
increaseArray(newLength);
listSize = maxSize + minSize;
for(int i = 0;i<minSize;i++)
{
element[i*2] = a.element[i];
element[i*2 + 1] = b.element[i];
}
copy(maxElement + minSize, maxElement + maxSize,element+2*minSize);
return *this;
}
///ex35.令a 和b 是类 arrayList 的两个对象。假设它们的元素从左到右非递减有序。
// 1 ) 编写方法 arrayList::merge(a,b),它生成一个新的有序线性表,包含a 和 的所有元
// 素。归并后的线性表是调用对象 *this。不要利用 STL 本数 merge。
// 2 ) 计算方法的复杂度。
// 3 ) 测试你的代码。
template<class T>
arrayList<T>& arrayList<T>::merge(arrayList<T>& a, arrayList<T>& b)
{
if(a.listSize == 0 && b.listSize == 0) return *this;
int minSize = a.listSize < b.listSize ? a.listSize:b.listSize;
int maxSize = a.listSize > b.listSize ? a.listSize:b.listSize;
int newLength = a.listSize > b.listSize ? a.arrayLength : b.arrayLength;
T* maxElement = a.listSize > b.listSize ? a.element:b.element;
if(minSize == 0) return *this;
if(maxSize + minSize > arrayLength)
{
newLength = a.arrayLength + b.arrayLength;
}
listSize = maxSize + minSize;
increaseArray(newLength);
int index = 0,aindex = 0,bindex = 0;
cout<<listSize<<endl;
for(int i = 0;i<listSize;i++)
{
if(aindex < a.size() && bindex < b.size())
{
if(a.element[aindex]<=b.element[bindex])
element[index] = a.element[aindex++];
else
element[index] = b.element[bindex++];
}
else
{
if(aindex < a.size() && bindex >= b.size())
element[index] = a.element[aindex++];
else if(aindex >= a.size() && bindex < b.size())
element[index] = b.element[bindex++];
}
}
return *this;
}
//30. 1 ) 编写方法 arrayList::split(lab),它生成两个线性表a 和b。a 包含 *this 中索引为偶
// 数的元素,b 包含其余的元素。
// 2 ) 计算方法的复杂度。
// 3 ) 测试你的代码。
template<class T>
arrayList<T>& arrayList<T>::split(arrayList<T>& a, arrayList<T>& b)
{
if(listSize == 0)
{
cout<<"listSize == empty";
return *this;
}
a.increaseArray(listSize);
b.increaseArray(listSize);
int index,aindex = 0,bindex = 0;
for(int i = 0;i < listSize; i++)
{
if(i % 2 == 0)
{
a.element[aindex++] = element[i];
}
else
{
b.element[bindex++] = element[i];
}
}
a.listSize = (listSize + 1) / 2;
b.listSize = listSize / 2;
return *this;
}
template<class T>
class stack
{
public:
virtual ~stack(){}
//返回true ,当且仅当栈为空
virtual bool empty() const = 0;
//返回栈中元素个数
virtual int size() const = 0;
//返回栈顶元素的引用
virtual T& top() = 0;
//删除栈顶元素
virtual void pop() = 0;
//将元素 theElement 压入栈顶
virtual void push(const T& theElement) = 0;
};
//从类 arrayList 和 stack 派生的类 derivedArrayStack。
//类 derivedArrayStack 的构造函数直接调用类 arrayList 的构造函数,动态创建一维数组,
//数组容量 ( 长度 ) 是参数 initialCapaticy 的值。initialCapaticy 的缺省值是 10。其他成员函数
//的代码也是直接调用基类的成员函数来实现的。
template <class T>
class derivedArrayStack : public arrayList<T>,
public stack<T>
{
public:
derivedArrayStack(int initialCapacity = 10)
:arrayList<T>(initialCapacity){}
bool empty() const
{
return arrayList<T>::empty();
}
int size() const
{
return arrayList<T>::size();
}
//函数top和pop都在类方法get和erase之前检查栈是否为空
//因为基类的方法get和erase在遇到空栈时将抛出异常
//所以我们可以从top和pop中删除对空栈的检查
//而不会影响程序结果。
T& top()
{
if(arrayList<T>::empty())
throw logic_error("空栈");
return arrayList<T>::get(arrayList<T>::size() - 1);
}
void pop()
{
if(arrayList<T>::empty())
throw logic_error("空栈");
arrayList<T>::erase(arrayList<T>::size() - 1);
}
void push(const T& theElement)
{
arrayList<T>::insert(arrayList<T>::size(),theElement);
}
};
//类 arrayStack
template<class T>
class arrayStack : public stack<T>
{
public:
arrayStack(int initialCapacity = 10);
~arrayStack(){delete [] stack;}
bool empty() const {return stackTop == -1;}
int size() const
{
return stackTop+1;
}
T& top()
{
if(stackTop == -1)
throw logic_error("stack empty");
return stack[stackTop];
}
void pop()
{
if(stackTop == -1)
throw logic_error("stack empty");
stack[stackTop--].~T(); //T的析构函数
}
void push(const T& theElement);
T* stack; //元素数组
private:
int stackTop;//当前栈顶
int arrayLength;//栈容量
};
template<class T>
arrayStack<T>::arrayStack(int initialCapacity)
{
//构造函数
if(initialCapacity < 1)
{
ostringstream s;
s << "Initial capacity = "<<initialCapacity<<"must be > 0";
throw logic_error(s.str());
}
arrayLength = initialCapacity;
stack = new T[arrayLength];
stackTop = -1;
}
template<class T>
void arrayStack<T>::push(const T& theElement)
{
//将元素 theElement 压入栈
if(stackTop == arrayLength - 1)
{
//空间已满,容量加们
changeLength1D(stack,arrayLength,2*arrayLength);
arrayLength *= 2;
}
//在栈顶插入
stack[++stackTop] = theElement;
}
//复杂度
//程序 8-6 的时间复杂度是 O(0),其中 )为输入表达式的长度。要理解这个结果需要注意,
//程序执行了 O(n) 次入栈和 O(n) 次出栈。尽管个别人栈操作时间的复杂度为 O( 容量 ) ( 因为
//数组容量加倍 ),但 O(n) 次入栈操作的时间复杂度依然是 O(n)。每一次出栈操作的时间复杂
//度是 O(1),因此 O(n) 次出栈操作的时间复杂度是 O(n)。
//列车车厢重排
//1. 问题描述
//一列货运列车有壮节车厢,每节车厢要停靠在不同的车站。假设 n个车站从1到n编号,
//而且货运列车按照从n到1的顺序经过车站。和车厢的编号与它们要停靠的车站编号相同。为
//了便于从列车上御掉相应的车厢,必须按照从前至后、从 1 到n 的顺序把车厢重新排列。这
//样排列之后,在每个车站只需印掉最后一节车厢即可。和车厅重排工作在一个转轨站 ( shunting
//yard ) 上进行,转轨站上有一个入轨道(input track )、一个出轨道(output track ) 和大个缓冲
//轨道 (holding track )。缓冲轨道位于入轨道和出轨道之间。图a 显示了一个转轨站,其中
//有3个缓冲轨道H1 、H2 和H3,即k=3。开始时,挂有半节车厢的货车开始在入轨道,而最
//后在出轨道上的顺序是从右到左,从 1 至 n。 在图a 中,n=9,和车厢从后至前的初始顺序为
//5,8,1,7,4,2,9,6,3。图b 是按要求的顺序重新排列的结果。
/*
[581742963] [897654321]
———————————————————————— ————————————————————————
入轨道 | | | 出轨道 | | |
H1 H2 H3 H1 H2 H3
*/
//2. 求解策略
//为了重排车厢,我们从前至后检查人轨道上的车厢。如果正在检查的车厢是满足排列要
//求的下一节车厢,就直接把它移到出轨道上。如果不是,就把它移到一个缓冲轨道上,直到
//它满足排列要求时才将它移到出轨道上。缓冲轨道是按照 LIFO 的方式管理的,车厢的进出
//都在缓冲轨道的顶部进行。在重排车厢过程中,仅允许以下移动:
//车厢可以从人轨道的前端 ( 即右端 ) 移动到一个缓冲轨道的顶部或出轨道的后端 ( 即左端)。
//车厢可以从一个缓冲轨道的顶部移到出轨道的后端。
//考虑图 a 的人轨道上的车厢排列。3 号车厢在人轨道上的前端
//但是不能将它移到出轨道上.因为1号和2 号车厢必须排在它前面
//因此,3号车厢被卸下,移到缓冲轨道
//入轨道上的下一节车厢是6号,也必须移到缓冲轨道。
//。如果把6号车厢移到H1,那么重排过程无法完成,因为3号车厢在6号车厢的下面
//它无法在6号车厢之前从H1进入出轨道
//于是要把6号车厢移到H2,入轨道上的下一节车厢是9号它被移到H3
//因为如果把它移到H1或H2,重排过程也无法完成。
//。请注意 : 当任何一条缓冲轨道上的车厢不是从顶到底按
//照递增序排列时,重排过程都无法完成。绥冲轨道的当前状态如图a 所示。
//接下来考虑2号车。它可以进入任何一个缓冲轨道,但是要优先选择H1。因为如果它
//进到H3那么缓冲负道就无法按排列要求容纳7号和8号车,如果2号车进入H2那么
//接下来的4号车而就必须进到H3这样一来缓冲轨道将无法按排列要求容纳5号、7号和8号车厢。
//对缓冲轨道选择的最基本的要求是编号为u的车应该进入的缓冲轨道,其顶部车厢编号是大于u的最小者
//我们将依据这条分配规则来选择缓冲轨道。
//当考虑4号车箱时,三个缓冲轨道顶部的车厢分别是2号、6号和9号。根据分配规则,
//4号车厢进到H2。然后7号车厢进到H3。图b 给出了缓冲轨道的当前布局。接下来是1
//号车厢,它直接进入出轨道。现在把 2 号车厢从 局1 移到出轨道。然后把 3 号车厢从 万1 移到
//出轨道,接着把4号车厢从H2移到出轨道。至此,没有可以立即进入出轨道的车厢了。
//接下来要进入缓冲站的是 8 号车,它被调人。然后是 5 号车厢,它从入轨道直接进入
//出轨道。然后依次把6号、7 号、8 号和 9 号车厢从它们所在的缓冲轨道移到出轨道。
//初始排列如图a所示的车厢,只需三个缓冲轨道就可以进行车啉重排,而按照其他初
//始顺序排列的车厢,可能需要更多的缓冲轨道才能重排。例如,初始排列为 1,m,m-1,2 的车厢需要 -1 个缓冲轨道。
//c++实现
//用k个数组栈来表示k个缓冲轨道。之所以使用数组栈,是因为它比链栈要快。程序是我们要
//使用的全局变量
arrayStack<int> *track; ///缓冲轨道数组
int numberOfCars;
int numberOfTracks;
int smallestCar; //在缓冲轨道中编号最小的车厢
int itsTrack; //停靠着最小编号车厢的缓冲轨道
//函数 railroad 计算一个车厢的移动序列,以此完成车厢的重排。车厢初始
//顺序为 inputOrder[l:theNumberOfCars],缓冲轨道最多为 theNumberOfTracks。如果移动序列
//不存在,railroad 的返回值是 false,和否则是 true。
//函数 railroad 从创建栈track开始,track[i] 代表缓冲轨道i,1 <= i <= numberOfTracks。
//for循环开始时,编号为 nextCarToOutput 的车厢并没有在缓冲轨道上。
//在for循环的第i次迭代中,人轨道上的车厢 inputOrder[i] 被调出。若 inputOrder[i]=
//nextCarToOutput,则该车厢直接被移到出轨道,然后 nextCarToOutput 的值增1。这时,绥
//冲轨道可能有若干节车厢可以进入出轨道,把这些车厢移到出轨道的过程由 while 循环完成。
//如果车厢 inputOrder[i] 不能移到出轨道,那么就没有车厢可以移到出轨道。这时,按照已经
//确定的轨道分配规则,把车是 inputOrder[i] 移到一个缓冲轨道。
//分别给出函数railroad中所调用的函数outputFromHoldingTrack和
//putInHoldingTrack。函数 outputFromHoldingTrack 用于把一节车厢从缓冲轨道移到出轨道,而
//上且修改 smallestCar 和 itsTrack 的值。函数 putInHoldingTrack 根据车厢分配规则把车厢 c 移到
//某个缓冲轨道,它也修改 smallestCar 和 itsTrack 的值。
//函数 outputFromHoldingTrack
void outputFromHoldingTrack()
{
// 将编号最小的车厢从缓冲轨道移到出轨道
//从栈 itsTrack 中删除编号最小的车顺
track[itsTrack].pop();
cout<<"Move car "<<smallestCar<<" from holding "
<<"track "<<itsTrack<<" to output track "<<endl;
//检查所有栈的栈顶,寻找编号最小的车和它所属的模itsTrack
smallestCar = numberOfCars + 2;
for(int i = 1; i <= numberOfCars; i++)
{
if(!track[i].empty() && (track[i].top() < smallestCar))
{
smallestCar = track[i].top();
itsTrack = i;
}
}
}
bool putInHoldingTrack(int c)
{
//将车厢c移到一个缓冲轨道。返回 false,当且仅当没有可用的缓冲轨道
//为车厢 c 寻找最适合的缓冲轨道
//初始化
int bestTrack = 0; //目前最合适的缓冲轨道
int bestTop = numberOfCars + 1; //取bestTrack 中顶部的车厢
//扫描缓冲轨道
for(int i = 1; i <= numberOfTracks; i++)
{
//缓冲轨道不空
if(!track[i].empty())
{
int topCar = track[i].top();
if(c < topCar && topCar < bestTop)
{
//缓冲轨道 i 的栈项具有编号更小的车厢
bestTop = topCar;
bestTrack = i;
}
}
else //缓冲轨道i为空
{
if(bestTrack == 0)
bestTrack = i;
}
if(bestTrack == 0)
return false;//没有可用的缓冲轨道
//把车c移到轨道bestTrack
track[bestTrack].push(c);
cout<<"Move car "<<c<<" from input track "
<<"to holding track "<<bestTrack<<endl;
//如果需要,更新 smallestCar 和 itsTrack
if(c < smallestCar)
{
smallestCar = c;
itsTrack = bestTrack;
}
return false;
}
}
bool railroad(int inputOrder[],int theNumberOfCars, int theNumberOfTracks)
{
//从初始顺序开始重排车箱
//如果重排成功,返回 true,否则返回 false
numberOfCars = theNumberOfCars;
numberOfTracks = theNumberOfTracks;
//创建用于缓冲轨道的栈
track = new arrayStack<int> [numberOfTracks + 1];
int nextCarToOutput = 1;
smallestCar = numberOfCars + 1;//缓冲轨道中无车厢
//重排车箱
for(int i = 1; i <= numberOfCars; i++)
{
if(inputOrder[i] == nextCarToOutput)
{
outputFromHoldingTrack();
nextCarToOutput++;
//从缓冲轨道移到出轨道
while(smallestCar == nextCarToOutput)
{
outputFromHoldingTrack();
nextCarToOutput++;
}
}
else
{
//将车箱 inputOorder[i] 移到一个缓冲轨道
if(!putInHoldingTrack(inputOrder[i]))
return false;
}
return true;
}
}
//开关盒布线
//1. 问题描述
//在开关盒布线问题中,给定一个矩形布线区域,其外围有若干管脚。两个管脚之间通过
//布设一条金属线路来连接。这条金属线路称为电线,它被限制在矩形区域内。两条电线交叉
//会发生电流短路。因此,电线不许交叉。每对要连接的管脚称为一个网组。对于给定的一些
//网组,我们需要确定,它们能否连接而又不发生交叉。图 a 是一个布线的示例,其中有8
//个管脚和4个网组。四个网组分别是(1, 4), (2, 3), (5,6) 和(7,, 8)。图 b 的布线
//在网组 (1,4) 和 (2,3 ) 之间有交叉,而图 c 的布线没有交叉。因为这 4个网组的布线
//可以没有交叉,所以这个开关盒称为可布线开关盒 ( routable switch box )。( 在现实问题中,
//两个相邻的电线之间还要求保留一个最小的间隙,但是我们忽略这个额外的要求。) 我们的问
//题是,输入一个开关盒布线实例,然后确定它是否可以布线。
/*
*/
//2. 求解策略
//为了解决开关售布线问题,我们注意到,当一个网组互连时,连线把布线区域分隔成两
//个分区。分区边界上的管脚属于哪一个分区与连线无关,而与互连网组的管肢有关。例如,
//当网组 (1,4 ) 互连时,就有两个分区。一个分区包含管脚 2 和3,另一个分区包含管脚
//5 ~ 8。现在如果有一个网组,其两个管脚分别属于两个不同的分区,那么这个网组是不可布
//线的,进而整个开关盒布线实例也是不可布线的。如果没有出现这样的网组,那么我们就可
//以根据连线不能跨区的原则,对每个分区是否可独立布线的问题做出判断。如果从一个分区
//中选择一个网组,这个网组把其所属分区分成两个子分区,而其余任一个网组的两个管脚都
//分属不同的子分区,那么就可以判断,这个分区是可布线的。
//为了实现这个策略,可以从任意一个管脚开始,按顺时针或逆时针方向沿着开关盒的边
//界进行遍历。如果从管脚 1 开始沿顺时针方向遍历图a的管脚,那么遍历的管脚顺序是 1,
//2,…,8。管脚 1 和4是一个网组,于是管脚 1 至4之间出现的所有管脚构成第一个分区
//管脚4至 1 之间出现的所有管脚构成另一个分区。把管脚 1 插入栈,然后继续处理,直到管
//脚 4。这个过程使我们仅在处理完一个分区之后才能进入下一个分区。下一个是管脚2,它
//与管脚 3 是一个网组,它们把当前分区分成两个分区。与前面的做法一样,把管脚 2 插入栈,
//然后继续处理,直到管脚 3。由于管脚 3 和管脚 2 是一个网组,而管脚 2 正处在栈顶,因此这
//表明已经处理完一个分区,可将管脚 2 从栈顶删除。接下来将遇到管脚 4,而与它同是一个网
//组的管脚 1 正处在栈项。现在,对一个分区的处理已经完毕,可从栈顶删除管脚 1。按照这种
//方法继续下去,我们可以完成对所有分区的处理,而且当 8 个管脚都检查之后,栈为空。
//当我们处理不可布线的开关盒时,将会出现什么样的情况呢? 假定图 a 的网组是 ( 1,
//5), (2,3), (4,7) 和(6, 8)。开始时,管脚 1 和 2 入栈。当检查到管脚 3 时,管脚 2 出栈。
//下一个是管脚 4,因为它与栈项的管脚不能构成一个网组,所以它人栈。当检查到管脚 5 时,
//它也人栈。尽管已经扫描到管靶 1 和管脚 5,但还不能结束由这两个管脚所定义的第一个分
//区的处理过程,因为管脚 4 的网组布线将不得不跨越这个分区的边界。结果是,当检查了所
//有的管脚时,栈不是空的。
//3. C++ 实现和时间复杂度
//一个网组编号。对于图 8-8c 的示例,输入数组 net 的值是 [1, 2, 2, 1, 3, 3, 4. 4]。该程序的复杂
bool checkBox(int net[], int n)
{
//确定开关盒是否可布线
///数组 net[0..n-1] 管角数组,用以形成网组n 是管脚个数
arrayStack<int>* s = new arrayStack<int>(n);
//按顺时针时针扫描网组
for(int i = 0; i < n; i++)
{
//处理管脚i
if(!s->empty())
{
//检查栈的顶部管脚
if(net[i] == net[s->top()])
{
//管脚 net [i] 是可布线的,从栈中删除
s->pop();
}
else
{
s->push(i);
}
}
else
{
s->push(i);
}
}
//是否有剩余的不可布线的管肢
if(s->empty())
{
//没有剩余的管脚
cout<<"Switch box is routable"<<endl;
return true;
}
cout<<"Switch box is not routable"<<endl;
return false;
}
//7.
//1 ) 对栈的 ADT 进行扩充,增加以下函数:
//i. 输入栈。
//将一个栈转变为一个适合输出的串。
//将一个栈分裂为两个栈。第一个栈包含从栈底开始的一半元素,第二个栈包含剩余元素。
//iv. 将两个栈合并,把第二个栈的所有元素置于第一个栈的顶部。不改变第二个栈中元素
//的相对顺序。
//2 ) 定义抽象类 extendedStack,它扩展抽象类 stack,而且包含与 1) 中函数对
//应的方法。
//4) 测试你的代码的正确性。
template<class T>
class extendedStack : public virtual stack<T>
{
public:
virtual std::istream& input(std::istream& in) = 0;
virtual std::string toString() const = 0;
virtual void split(extendedStack<T>& st1,
extendedStack<T>& st2) = 0;
virtual void merge(extendedStack<T>& st2) = 0;
};
template<class T>
class extendedArrayStack : public arrayStack<T>,
public extendedStack<T>
{
template<class U>
friend std::istream& operator>>(std::istream& in,
extendedArrayStack<U>& st);
template<class U>
friend std::ostream& operator<<(std::ostream& out,
const extendedArrayStack<U>& st);
public:
extendedArrayStack<T>(int initialCapacity = 10)
:arrayStack<T>(initialCapacity)
{
}
virtual std::istream& input(std::istream& in) override;
virtual std::string toString() const override;
virtual void split(extendedStack<T>& st1,
extendedStack<T>& st2);
virtual void merge(extendedStack<T>& st2);
virtual bool empty() const override
{
return arrayStack<T>::empty();
}
virtual int size() const override
{
return arrayStack<T>::size();
}
virtual T& top() override
{
return arrayStack<T>::top();
}
virtual void pop() override
{
arrayStack<T>::pop();
}
virtual void push(const T& theElement) override
{
arrayStack<T>::push(theElement);
}
std::ostream& output(std::ostream& out) const
{
out<<toString();
return out;
}
};
template<class T>
std::istream& extendedArrayStack<T>::input(std::istream& in)
{
T t;
while(in >> t)
{
push(t);
}
return in;
}
template<class U>
std::istream& operator>>(std::istream& in, extendedArrayStack<U>& st)
{
st.input(in);
return in;
}
template<class U>
std::ostream& operator<<(std::ostream& out,
const extendedArrayStack<U>& st)
{
st.output(out);
return out;
}
template <class T>
std::string extendedArrayStack<T>::toString() const
{
std::string s = "";
for(int i = 0; i < size(); i++)
{
s += std::to_string(arrayStack<T>::stack[i]);
s += " ";
}
return s;
}
template<class T>
void extendedArrayStack<T>::split(extendedStack<T>& st1,
extendedStack<T>& st2)
{
auto& st1_t = dynamic_cast<extendedArrayStack<T>&>(st1);
auto& st2_t = dynamic_cast<extendedArrayStack<T>&>(st2);
int i = 0;
for(;i < size() / 2;i++)
{
st1_t.push(arrayStack<T>::stack[i]);
}
for(;i<size();i++)
{
st2_t.push(arrayStack<T>::stack[i]);
}
}
template<class T>
void extendedArrayStack<T>::merge(extendedStack<T>& st2)
{
auto& st_t = dynamic_cast<extendedArrayStack<T>&>(st2);
for(int i = 0; i < st_t.size();i++)
{
push(arrayStack<T>::stack[i]);
}
}
//离线等价类问题
//1. 问题描述
//离线等价类问题的定义见 6.5.4 节。这个问题的输入是元素数目n、关系对数目r以及r
//个关系对。目标是把元素划分为等价类。
//2. 求解策略
//求解分为两个阶段。在第一个阶段,我们输入数据,建立n表以表示关系对。对每一
//个关系对(i,j),守放在list[j],j放在 list[i]。
//例 8-3 假定n=9, r=11,且11个关系对是 (1,3),(1,6),(3,7),(4,8),(5,2),(6,3),(4.9),
//(9,7),(7,8),(3,4),(6,2)。9 个表是
/*
list[1] = [5,6]
list[2] = [5,6]
list[3] = [7,4]
list[4] = [8,9,3]
list[5] = [1,2,6]
list[6] = [1,2,5]
list[7] = [3,9,8]
list[8] = [4,7]
list[9] = [4,7]
*/
//表中元素的顺序不重要。
//在第二个阶段是寻找等价类。为寻找一个等价类,首先要找到该等价类中第一个没有
//输出的元素。这个元素作为该等价类的种子。该种子作为等价类的第一个成员输出。从这个
//种子开始, 我们找出该等价类的所有其他成员。种子被加到一个表 unprocessedList 中。从表
//unprocessedLis 中删除一个元素i,然后处理表list[i]。list[i]中所有元素和种子同属一个等价
//类;将list[i]中还没有作为等价类成员的元素输出,然后加入 unprocessedList 中。这是一个
//过程 : 从表 unprocessedLis 中删除一个元素,然后把表list[i]中还没有输出的元素输出,并
//且加入 unprocessedList 中。这个过程持续进行到 unprocessedList 为空。这时我们就找到了一
//个等价类,然后继续寻找下一个等价类的种子。
//例8-4 考虑例 8-3 令 1 是第一个种子,作为一个等价类的成员被输出,然后加入表
//unprocessedList 中。接下来把 1 从 unprocessedList 中删除,然后处理 list[1]。元素5和6属
//list[1],与1同属一个等价类,它们被输出,然后加入 unprocessedList 中。 将5或6从
//unprocessedList 中删除,然后处理它们所在的表。假定删除的是5。考察 list[5] 中的元素
//1、2和6。因为1和6已经输出,所以被忽略。把元素2输出,然后加入 unprocessedList
//中。当 unprocessedList 中的剩余元素 (6 和2 ) 被删除和处理,没有其他元素被输出或加入
//unprocessedList 时,unprocessedList 成为空表,这时我们便找到了一个等价类。
//为找到另一个等价类,我们要寻找一个种子,它是还没有输出的元素。元素 3 还没有给
//出,因此可以作为下一个等价类得种子。元素3、4、7、8 和 9 作为这个等价类的元素被输出
//这时不再有种子,因此我们找到了所有等价类。
//C++ 实现
//为了实现上述算法,我们必须选择表 list 和 unprocessedList 的描述方法。表 list 上的操作
//是插入和检查所有元素。因为元素在 list 中的插入位置并不重要,所以用任何线性表或栈来
//描述都可以。选择的标准是空间和时间性能最优。
//在个表 list[1:m] 中,元素总数为 2r。所以,就空间需求而言,数组线性表和栈类需要
//的空间所能容纳的元素个数为 2 和 4r ( 因为数组容量加倍,所以数组长度最多可以达到数组
//元素个数的两倍 )。链表类需要的空间要能容纳 27 个元素和 2r个指针。我们对线性表和栈的
//时间性能研究表明,这些结构的链表实现比数组
//实现要慢。因此,我们在对离线等价类问题做进一步研究时,不考虑链表表示法。
//如果在表的右端插入新元素,那么应用 arrayList将有更好的时间性能。然
//而,使用 arrayStack 性能会更好一点。从性能上考虑,线性表 unprocessedList 也用 arrayStack
//来实现。
//程序 给出了解决离线等价类问题的 C++ 程序,它由两部分组成。在程序的第
//一部分,输入n,r和r对关系,对于每个元素都建立了一个相应的栈。栈 list[i]相对应元素i,
//它包含所有这样的元素j:(i,j) 或 (j,i) 是输入的关系对。如果通过检验可以保证对每一个
//输入对 (a,b),a和b都属于 [1,h],那么代码会更易维护。练习 31 要求改进代码,增加对
//程序的第二部分是输出等价类。其中使用了数组 out,而且 out[i] = true,当且仅当i
//已经作为某个等价类的元素而输出。栈 unprocessedList 辅助寻找一个等价类的所有元素。这
//个栈中的元素都作为当前等价类的元素被输出,并且用来寻找当前等价类的其他元素。为寻
//找下一个等价类的种子,我们扫描数组 out 以寻找一个尚未输出的元素。如果没有这样的元
//素,就没有下一个等价类。如果有,则开始寻找下一个等价类。
/*
int main()
{
int n;//元素的个数
int r;//关系个数
cout<<"Enter number of elements"<>n;
if(n<2)
{
cout<<"Too few elements"<>r;
if(r<1)
{
cout<<"Too few relations"<* list = new arrayStack[n+1];
///输入r个关系,存储在表中
int a,b; //(a,b) 是一个关系
for(int i = 1; i<=r;i++)
{
cout<<"Enter next relations/pair"<>a>>b;
list[a].push(b);
list[b].push(a);
}
//初始化以输出等价类
arrayStack unprocessedList;
bool *out = new bool[n+1];
for(int i = 1;i <= n;i++)
{
out[i] = false;
}
//输出等价类
for(int i = 1;i <= n; i++)
{
if(!out[i])
{
//启动一个新类
cout<<"Next class is:"<
//复杂度分析
//为了分析等价类程序的复杂度,我们假设没有异常抛出。程序第一部分用时O(n+r)
//在程序的第二部分,每个元素只输出一次,只入栈unpdrocessedList一次,只从栈
//unpdrocessedList中出栈一次,因此,入栈和出栈操作所需要的总时间为O(n)。最后,当一个
//元素从栈 unpdrocessedList 中出栈时,list[i]中的所有元素要出栈接受检查。
//每个list[j]中的每一个元素只出栈一次。所以,在所有 list[1:m] 中的所有元素出栈接受检查所需要的时间为
//O(r) (注意,在输入阶段之后,所有 list[1:mq] 中的元素总数是 2*r )。对于程序的总时间
//因为解决离线等价类问题的每一个程序对每一个关系和元素都至少考察一次,所以用时
//迷宫老鼠
//问题描述
//迷宫是一个矩形区域,有一个人口和一个出口。迷宫内部包含不能穿
//越的墙壁或障碍物。这些障碍物沿着行和列放置,与迷宫的边界平行。迷宫的和人口在左上角,
//出口在右下角。
//假定用nxm的矩阵来描述迷宫,和矩阵的位置 (1,1) 表示人口,(n,m) 表示出口
//n和m分别代表迷宫的行数和列数。迷宫的每个位置都可用其行号和列号表示。在矩阵中,当且
//仅当在位置(i,j)处有一个障碍时,其值为1,否则其值为 0。图给出了图中的迷宫
//所对应的矩阵表示。
//迷宫老鼠 ( rat in a maze ) 问题是要寻找一条从人口到出口的路径。路径
//是一个由位置组成的序列,每一个位置都没有障碍,而且除入口之外,路径上的每个位置都
//是前一个位置在东、南 、西或北方向上相邻的一个位置 ( 如图所示 )。
/*
0 1 1 1 1 1 0 0 0 0
0 0 0 0 0 1 0 1 0 0
0 0 0 1 0 1 0 0 0 0
0 1 0 1 0 1 0 1 1 0
0 1 0 1 0 1 0 1 0 0
0 1 1 1 0 1 0 1 0 1
0 1 0 0 0 1 0 1 0 1
0 1 0 0 1 1 1 0 1 0
1 0 0 0 0 0 0 1 0 0
0 0 0 0 0 1 1 1 1 0
N
|
W<-------->E
|
S
*/
//我们要编写程序来解决迷宫老鼠问题。 假设迷宫是一个方阵 ( 即 m=n ) 旦足够小,能够
//整个存储在目标计算机的内存中。程序应是独立的,一个用户可以输入自己选择的迷宫来直
//接寻找迷宫路径。
//2. 设计
//我们将采用自顶向下的模块化方法来设计这个程序。不难理解,这个程序有三个部分 ;
//输入迷宫、寻找路径和输出路径。每个部分都用一个程序模块来实现。还有一部分用于显示
//欢迎信息、软件名称及作者信息,这部分用第四个模块来实现,这个模块主要是为了增强程
//序界面的友好性,它与我们要编写的程序没有任何直接关系。
//寻找路径的模块不直接与用户打交道,因此没有提供帮助机制,也不是由菜单驱动的。
//其他三个模块都与用户进行交互,因此应多花一些精力来设计用户接口。友好的用户接口能
//让用户更喜欢你的程序。
//外此处是函数 welcome
//此处是函数 inputMaze
//此处是函数 findPath
//由此处是函数 outputPath
/*
void main()
{
welcome();
inputMaze();
if(findPath())
{
outputPath();
}
else
{
cout<<"No path"<
/*
bool findPath()
{
寻找迷宫中到达出口的一条路径
if(路径找到)
return true;
else
return false;
}
*/
//C++ 代码之前,首先要明白如何寻找迷宫路
//径。首先把迷宫的入口作为当前位置。如果
//当前位置是迷宫出口,那么已经找到了一条路径,寻找工作结束。如果当前位置不是迷
//富出口,则在当前位置上放置障碍物,以阻
//止寻找过程又绕回到这个位置。然后检查相邻位置是否有空闲 ( 即没有障碍物 ),如果有,就
//移动到一个空闲的相邻位置上,然后从这个位置开始寻找通往出口的路径。如果不成功,就
//选择另一个空闲的相邻位置,并从它开始寻找通往出口的路径。为了方便移动,在进入新的
//相邻位置之前,把当前位置保存在一个栈中。如果所有空闲的相邻位置都已经被探索过,但
//还未能找到路径,则表明迷宫不存在从人口到出口的路径。
//让我们使用上述策略来考察图 8-9 的迷宫。首先把位置 (1,1 ) 插入栈,并从它开始进
//行寻找,移到与它相邻的唯一的空闲位置 (2,1 ),并在位置( 1,1 ) 上放置障碍物,以防止
//以后的寻找过程再经过这个位置。从位置 (2,1 ) 可以移动到(3,1 ) 或 (2,2 )。假定移动
//到位置(3,1 )。在移动之前,先在位置 (2,1 ) 上放置障碍物并将 (2,1 ) 插入栈。从位置
//(3,1 ) 可以移到(4,1 ) 或(3,2 )。如果移到 (4,1 ), 那么要在 (3,1 ) 处放置障碍物,
//并把 (3,1 ) 插入栈。从 (4, 1 ) 依次移动到(5, 1)、(6, 1)、(7, 1) 和(8, 1 )。移到 (8,
//1 ) 以后无路可走。此时的栈包含着从 (1,1 ) 至 (8,1 ) 的路径。为了寻找其他路径,从栈
//中删除(8,1 ),回退至 (7,1 ),由于(7,1 ) 也没有新的空闲的相邻位置,因此从栈中删
//除位置 (7,1 ),回退至 (6,1 )。按照这种方式,一直要回退到 (3,1 ),然后才可以继续移
//动 (即移动到 (3,2 ))。注意,在栈中始终有一条从人口到当前位置的路径。如果最终到达
//到当前位置的路径。如果最终到达了出口,那么栈中的路径就是从入口到出口的路径。
//为了细化图 8-14,我们需要把迷宫 (一个0和 1 的矩阵 )、迷宫的每个位置以及栈都表
//示出来。首先考虑迷宫。迷宫一般被描述成一个 int 类型的二维数组 maze。( 由于每个数组
//的位置仅有0或 1 两种取值,因此可以用 bool 型二维数组,true 代表 1,false 代表 0。这样,
//表示迷宫的数组空间就被减少了。 ) 迷宫和矩阵的位置 (i,j ) 对应于数组 maze 的位置 [中。
//从迷宫的内部位置 ( 非边界位置 ) 开始,有 4 种可能的移动方向 : 右、下、左和上。从
//迷富的边界位置开始,只有两种或三种可能的移动方向。为了避免在处理内部位置和边界位置时存在差别,
//可以在迷宫的周围增加一圈障碍物。对于一个mxm的数组 maze,这一圈障碍物将占据数组 maze 的第0行、
//第m+1行、第0列和第m+1列 (如图8-15 所示)
//现在,迷宫的所有位置都处在一圈障碍物所围成的边界之内,从迷宫的每个位置开始,都有4种可能
//的移动方向 ( 可能每个方向都有障碍物 )。因为给迷宫围上了一圈障碍物,所以程序不再需要处理边界条件,图
// 设有一圈障碍物的的迷宫
//这就大大简化了代码设计。这种简化的代价是迷宫数组的空间稍稍增加了。
//每个迷宫位置都可以用行和列的下标来表示,分别称为迷宫位置的行坐标和列坐标。可
//以定义一个带有数据成员 row 和 col 的类 position,使用它的对象来跟踪记录迷宫位置。用数
//组表示栈,栈用来保存从人口到当前位置的路径。一个没有障碍物的mxm迷宫,最长的路
//径可包含m^2个位置。
//因为路径包含的位置没均不相同,而且迷宫仅有 m^2 个位置,所以一条路径所包含的位置
//最多不超过 m^2。又因为路径的最后一个位置不必存储到栈中,所以在栈中存储的位置最多是
//注意,在一个没有障碍物的迷宫中,在人口和出口之间,总有一条最多包含 2m个位
//置的路径。不过,我们现在无法保证寻找路径的程序模块能够找到最短
/*
bool findPath()
{
//找一条从入口 (1,1) 到出口 (mxm) 的路径
//初始化迷宫四周的围墙
//初始化变量,以记录我们在迷宫的当前位置
here.row = 1;
here.col = 1;
maze[1][1] = 1;
//防止返回到入口
//寻找通向出口的路径
while(不是出口) do
{
//寻找可以移动的下一步
if(下一步存在)
{
//把下一步的位置压进路径栈
//走到下一步,然后在这一步加上障碍物
here = neighbor;
maze[here.row][here.col] = 1;
}
else
{
//不能继续往下走,退回
if(路径为空) return false;
//退回的位置在路径栈的顶部
}
}
return true;
}
*/
//现在的问题是,要确定从位置 here 开始向哪一个相邻位置移动。如果用一种系统方式来
//选择,那么问题就简化了。例如,首先尝试向右移动,然后向下和向左,最后向上。一旦选
//择了要移动的位置,就要知道该位置的坐标。而利用一个如图 8-18 所示的偏移量表,就很容
//offset[i].row 和 offset[il.col 分别是从当前位置沿方向i 移动到下一个相邻位置时,row 和 col 坐
//标的增量。 例如,如果当前位置是 (3,4),则其右边相邻位置的行坐标为 3 + offset[0].row=3,
//列坐标为 4+offset[0].col=5。
/*
移动 方向 行偏移 列偏移
0 右 0 1
1 下 1 0
2 左 0 -1
3 上 -1 0
*/
//为了不重蹈已经走过的位置,我们在每一个走过的位置 maze[i][j] 上设置障碍物 ( 即令
//maze[i][j] = 1
//把上述细化工作并入图 8-17 的代码中,就得到了程序 8-15 的 C++ 代码。在程序 8-15 的
//代码中,变量 size 存储着迷宫的行和列的大小。
struct position
{
int row;
int col;
};
/*
bool findPath()
{
arrayStack* path;
// 寻找一条从入口 (1,1) 到达出口 (size,size) 的路径
//如果找到,返回 true,否则返回 false
path = new arrayStack;
//初始化偏移量
position offset[4];
offset[0].row = 0;offset[0].col = 1; //右
offset[1].row = 1;offset[1].col = 0; //下
offset[2].row = 0;offset[2].col = -1; //左
offset[3].row = -1;offset[3].col = 0; //上
//初始化迷宫外围的障碍墙
for(int i = 0; i <= size + 1;i++)
{
maze[0][i] = maze[size-1][i] = 1; //底部和顶部
maze[i][0] = maze[i][size + 1] = 1; //左和右
}
position here;
here.row = 1;
here.col = 1;
maze[1][1] = 1; //防止回到入口
int option = 0; //下一步
//寻找一条路径
while(here.row != size || here.col != size)
{
//没有到达出口
//找到要移动的相邻的一步
int r,c;
while(option <= lastOption)
{
r = here.row + offset[option].row;
c = here.col + offset[option].col;
if(maze[r][c] == 0) break;
option++; //下一个选择
}
//相邻的一步是否找到
if(option <= lastOption)
{
//移到maze[r][c]
path->push(here);
here.row = r;
here.col = c;
maze[r][c] = 1; // 设置 1 ,以防重复访问
option = 0;
}
else
{
//没有叙近的一步可走,返回
if(path->empty())
return false; //没有位置可返回
position next = path->top();
path->pop();
if(next.row == here.row)
option = 2 + next.col - here.col;
else
option = 3 + next.row - here.row;
here = next;
}
}
return true; //到达出口
}
*/
//函数 findPath 首先创建一个空栈。然后对偏移量数组进行初始化,并在迷宫周于设置一
//圈障碍物。在 while 循环中,从当前位置 here 出发,按右、下、左、上的顺序选择下一个移
//动位置。如果存在下一个移动位置,则将当前位置插入栈,然后移动到下一个位置。如果不
//存在下一个移动位置,则退回到前一个位置。如果无路可退 ( 即栈为空 ),则表明不存在通往
//出口的路径。如果可以退,那么当退到栈的顶部元素所表示的位置 (next) 时,就从 next 和
//here 来计算下一个移动位置。注意 here 与 next 相邻。实际上,在程序前面某一时刻,我们从
//next 移到 here,而且是最后一次移动。对下一个移动位置的选择可用以下代码来实现:
/*
if(next.row == here.row)
option=2+next.col - here.col;
else
option = 3+next.row - here.row;
*/
//现在分析程序的时间复杂度。在最坏情况下,可能要饥历每一个空闲位置,而每个空闲
//位置进入栈的机会最多有 3 次。( 每次从一个位置移动时,该位置都要插入栈,而从任何一个
//位置开始,最多有 3 种移动选择。 ) 因而每个位置从栈中被删除的机会也最多有 3 次。在每个
//位置上,检查相邻位置所需要的时间是O(1)。因此,程序的时间复杂度应为 O(unblocked),
//其中 unblocked 是迷宫的空闲位置数目。这个复杂度是 O(size^2)= O(m^2)。
//括号匹配
//问题描述 0 1 2 3 4 5 6 7 8 9
//我们要做的是: 对一个字符串的左右括号进行匹配。例如,字符串( a * ( b + c ) + d)在位
//置0和3有左括号,在位置7和10有右括号。位置0的左括号与位置10的右括号匹配,位置 3 的左括号
//与位置7的右括号匹配。在字符串 ( a + b )) (中,位置 5 的右括号没有与之匹配的左括号,
//位置6的左括号没有与之匹配的右括号。我们的目标是编写一个C++程序,其输入是一个字符串,
//输出是匹配的括号以及不匹配的括号。注意,括号匹配问题等价于 C++ 程序中的纯匹配问题。
//2. 求解策略
//通过观察可以发现,如果从左至右地扫描一个字符串,那么每一个右括号都与最近扫描
//的那个未匹配的左括号相匹配。这种观察结果促使我们在从左至右的扫描过程中,将扫描到
//的左括号保存到栈中。每当扫描都一个右括号,就将它与栈顶的左括号 ( 如果存在 ) 相匹配,
//并将匹配的左括号从栈顶删除。
//3. C++ 实现
//输出匹配的括号
void printMatchedPairs(const string& expr)
{
//括号匹配
arrayStack<int> s;
int length = (int)expr.size();
ostringstream oss;
// 扫描表达式 expr 寻找左括号和右括号
for(int i = 0; i < length; i++)
{
if(expr.at(i) == '(')
s.push(i);
else if(expr.at(i) == ')')
try
{
// 从栈中删除匹配的左括号
oss<<s.top()<<' '<<i<<endl;
s.pop();//没有栈匹配
}
catch(...)
{
//栈为空 没有匹配的左括号
cout<<"No match for right parentheis"<<" at "<<i<<endl;
}
}
//栈不为空。剩余在栈中的左括号是不匹配的
while(!s.empty())
{
cout<<"No match for left parentheis at "<<s.top()<<endl;
s.pop();
}
cout<<"matched '(' and ')' found at "<<oss.str()<<endl;
}
//15. 编写一个程序,判定字符串中是否有不匹配的括号,不许使用栈。测试你的程序。计算时
//间复杂度。
bool unmatchedParen(std::string& expr)
{
int count = 0;
for(int i = 0; i < expr.size(); ++i)
{
if(expr[i] == '(')
++count;
else if(expr[i] == ')')
--count;
if(count < 0)
return false;
}
if(count > 0)
return false;
return true;
}
void printMatchedParentsNoStack(const std::string& expr)
{
std::string s(expr);
ostringstream oss;
for(int i = 0; i < s.size(); ++i)
{
bool leftFound = false;
for(int j = 0; j < s.size(); ++j)
{
if(s[j] == '(')
{
leftFound = true;
bool rightFound = false;
int k = j + 1;
for(;k < s.size();++k)
{
if(s[k] == '(')
{
j = k;
}
else if(s[k] == ')')
{
rightFound = true;
break;
}
}
if(rightFound)
{
oss<<'(' << j <<','<<k<<')';
s[j] = ' ';
s[k] = ' ';
cout<<s<<endl;
break;
}
else
{
cout<<"unmatched '(' found at "<<j<<endl;
s[j] = ' ';
}
}
else if(s[j] == ')' && !leftFound)
{
cout<<"unmatched ')' found at "<<j<<endl;
s[j] = ' ';
}
}
if(!leftFound) break;
}
cout<<"matched '(' and ')' found at "<<oss.str()<<endl;
}
//ex16. 编写程序 8-6 的另一个版本,寻找匹配的圆括号和匹配的方括号。在字符串
//(a+[b*(c-d)+f]) 中,匹配的结果是 (0,14),(3,13),(6,10);
//在字符串 (a+[b*(c-d)+f)) 中,却存在一个嵌套问题
//内套问题 : 位置6的左圆括号应该在其后的右方括号出现之前和一个右圆括号匹配。测试
//你的代码。
void printMatchedPairs2(const std::string& expr)
{
arrayStack<int> st;
arrayStack<char> st2;
int length = expr.size();
ostringstream oss;
for(int i = 0; i < length; ++i)
{
switch(expr[i])
{
case '(':
case '{':
st.push(i);
st2.push(expr[i]);
break;
case ')':
if(!st.empty() && st2.top() == '(')
{
oss << '(' <<st.top()<<','<<i<<") ";
st.pop();
st2.pop();
}
else if(!st.empty() && st2.top() == '[')
{
cout<<"unmatched '[' and ')' found at "<<'[' <<st.top()<<','<<i<<").both of them will be dropped"<<endl;
st.pop();
st2.pop();
}
else
{
cout<<"unmatched "<<expr[i]<<" found at "<<i<<endl;
}
break;
case ']':
if(!st.empty() && st2.top() == '[')
{
oss<<'['<<st.top()<<','<<i<<"] ";
st.pop();
st2.pop();
}
else if(!st.empty() && st2.top() == '(')
{
cout<<"unmatched '(' and ']' found at "<<'('<<st.top()<<','<<i<<"],both of them will be dropped "<<endl;
st.pop();
st2.pop();
}
else
{
cout<<"unmatched "<<expr[i]<<" found at "<<i<<std::endl;
}
}
}
while(!st.empty())
{
cout<<"unmatched "<<st2.top()<<" found at "<<st.top()<<endl;
st.pop();
st2.pop();
}
cout<<"matched ' '(/[' and ')/]' found at '"<<oss.str()<<endl;
}
//ex17. 对一个包含圆括号、方括号和花括号的表达式完成练习 16。
void printMatchedPairs3(const std::string& expr)
{
arrayStack<int> st;
arrayStack<char> st2;
int length = expr.size();
ostringstream oss;
for(int i = 0; i < length; ++i)
{
switch(expr[i])
{
case '(':
case '[':
case '{':
st.push(i);
st2.push(expr[i]);
break;
case ')':
if(!st.empty() && st2.top() == '(')
{
oss << '(' <<st.top()<<','<<i<<") ";
st.pop();
st2.pop();
}
else if(!st.empty() && st2.top() == '[')
{
cout<<"unmatched '[' and ')' found at "<<'[' <<st.top()<<','<<i<<").both of them will be dropped"<<endl;
st.pop();
st2.pop();
}
else if(!st.empty() && st2.top() == '{')
{
cout<<"unmatched '{' and ')' found at "<<'{' <<st.top()<<','<<i<<").both of them will be dropped"<<endl;
st.pop();
st2.pop();
}
else
{
cout<<"unmatched "<<expr[i]<<" found at "<<i<<endl;
}
break;
case ']':
if(!st.empty() && st2.top() == '[')
{
oss<<'['<<st.top()<<','<<i<<"] ";
st.pop();
st2.pop();
}
else if(!st.empty() && st2.top() == '(')
{
cout<<"unmatched '(' and ']' found at "<<'('<<st.top()<<','<<i<<"],both of them will be dropped "<<endl;
st.pop();
st2.pop();
}
else if(!st.empty() && st2.top() == '{')
{
cout<<"unmatched '{' and ']' found at "<<'{'<<st.top()<<','<<i<<"],both of them will be dropped "<<endl;
st.pop();
st2.pop();
}
else
{
cout<<"unmatched "<<expr[i]<<" found at "<<i<<std::endl;
}
case '}':
if(!st.empty() && st2.top() == '{')
{
oss<<'{'<<st.top()<<','<<i<<"} ";
st.pop();
st2.pop();
}
else if(!st.empty() && st2.top() == '(')
{
cout<<"unmatched '(' and '}' found at "<<'('<<st.top()<<','<<i<<"},both of them will be dropped "<<endl;
st.pop();
st2.pop();
}
else if(!st.empty() && st2.top() == '[')
{
cout<<"unmatched '[' and ')' found at "<<'[' <<st.top()<<','<<i<<").both of them will be dropped"<<endl;
st.pop();
st2.pop();
}
else
{
cout<<"unmatched "<<expr[i]<<" found at "<<i<<std::endl;
}
}
}
while(!st.empty())
{
cout<<"unmatched "<<st2.top()<<" found at "<<st.top()<<endl;
st.pop();
st2.pop();
}
cout<<"matched ' '{(/[' and ')/]}' found at '"<<oss.str()<<endl;
}
//一个简洁的解决方法是递归。为了把最大的碟子移到塔 2 的底部,必须把其余n-1个蝶
//子移到塔 3,然后把最大的碟子移到塔 2。接下来是把塔3上的n-1个碟子移到塔2。为此可
//以利用塔 2 和塔 1。可以完全忽略塔 2 上已有的一个碟子,因为这个碟子比塔 3 上将要移过
//来的所有碟子都大,在它顶上可以堆放任何一个碟子。
//第一种实现方法
//程序给出了按递归方式求解汉诺塔的 C++ 代码。初始调用语句是
//towersOfHanoi(n,1,2,3)
void towersOfHanoi(int n, int x,int y, int z)
{
//把塔x顶部的n个蝶子移到塔y
if(n > 0)
{
towersOfHanoi(n-1,x,z,y);
cout<<"Move top disk from tower "<<x<<" to top of tower "<<y<<endl;
towersOfHanoi(n-1,z,y,x);
}
}
//5. 第二种实现方法
//程序1的输出是把碟子从塔1移到塔2的移动次序。假定我们要显示出每次移动之后
//三座塔的布局 (即塔上的碟子和它们从底到项的次序 ),那就必须在内存中保留这些布局,并
//在每次移动碟子之后对塔的布局进行修改。这样每移动一个碟子,就可以在一个输出设备
//(如计算机屏幕、打印机、录像机 ) 上输出塔的布局。
//从每个塔上移走碟子是按照 LIFO 方式进行的,因此可以把每个塔表示成一个栈。三座
//塔在任何时候都总共有n个碟子,因此,如果使用链表形式的栈,只需申请n个元素空间 ;
//如果使用数组形式的栈,那么因为塔 1 和塔 2 的容量都必须是m,塔 3 的容量必须是n-1,因
//此所需要的总空间为 3n-1。前面的分析已经指出,汉诺塔问题的复杂度是以二为指数的函数,
//因此,在可以接受的时间范围内,只能解决值比较小(如半和30 ) 的汉诺塔问题。对于这
//些比较小的n值,数组形式的栈和链表形式的栈在空间需求上差别相当小,因此用哪一种都
//可以。但是,数组形式的栈比链表形式的栈运行速度要快,因此我们还是用数组形式的栈。
//使用了数组描述的栈。towersOfHanoi(n) 仅仅是递归 moveAndShow 的预处
//理程序,moveAndShow 是以程序1为模式来设计的。预处理程序创建三个堆栈 tower[1:3]
//用来储存 3 座塔的布局。所有碟子从 1 ( 最小的碟子 ) 到n ( 最大的碟子 ) 编号。因为碟子用
//整数来模拟,所以栈元素类型为int。初始布局是所有碟子在 tower[1] 中,其他两座塔为空。
//构建好初始布局之后,预处理程序调用函数 moveAndShow。
//全局变量 ,tower[1:3] 表示三个塔
extendedArrayStack<int> tower[4];
void showState()
{
for(int i = 1;i < 4; i++)
{
std::cout<<"tower "<<i<<":"<<tower[i]<<endl;
}
}
void moveAndShow(int n,int x,int y,int z)
{
//把塔x 顶部的 n 个碟子移到塔 y,显示移动后的布局
//用塔 z 作为中转站
if(n > 0)
{
moveAndShow(n-1,x,z,y);
int d = tower[x].top(); //把一个碟子
tower[x].pop(); //从塔x 的顶部移到
tower[y].push(d); //塔Y的顶部
showState();
moveAndShow(n-1,z,y,x);
}
}
void towersOfHanoi(int n)
{
// 函数 moveandshow 的预处理程序
for(int d = n; d > 0; d--) //初始化
{
tower[1].push(d); //把碟子d加到塔1
}
//把 个碟子从塔 1 移到塔 3,用塔 2 作为中转站
moveAndShow(n,1,2,3);
}
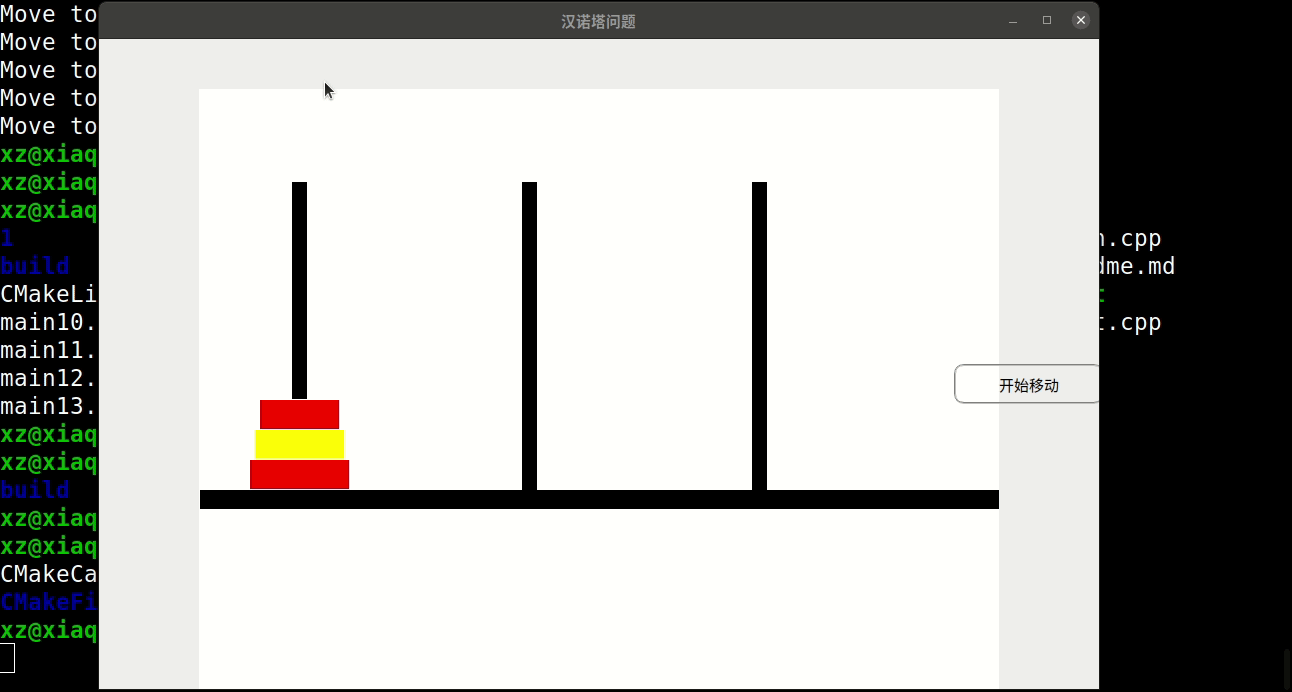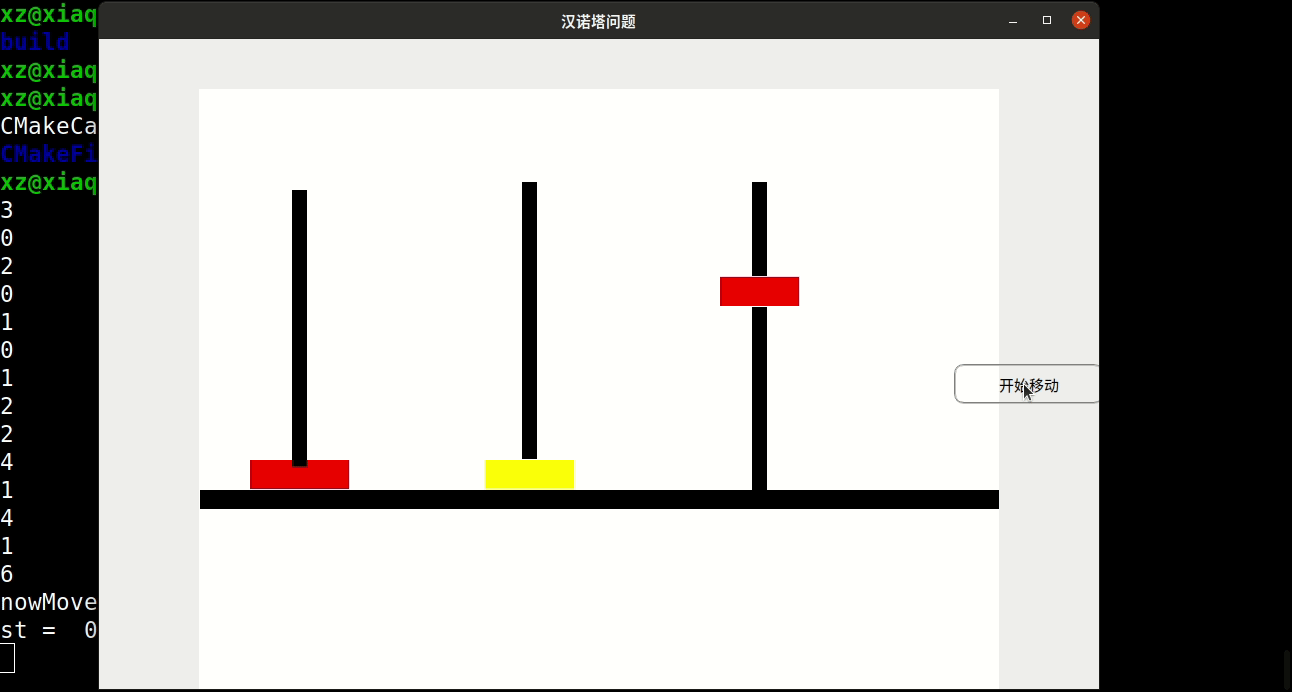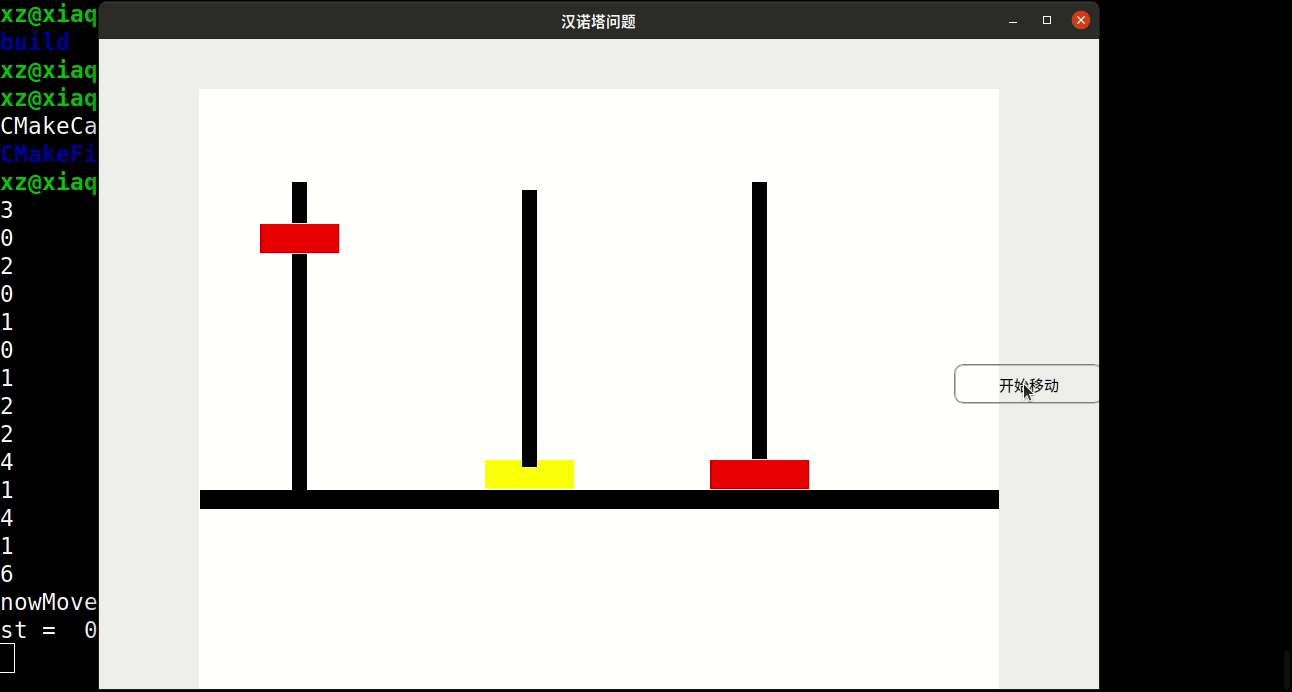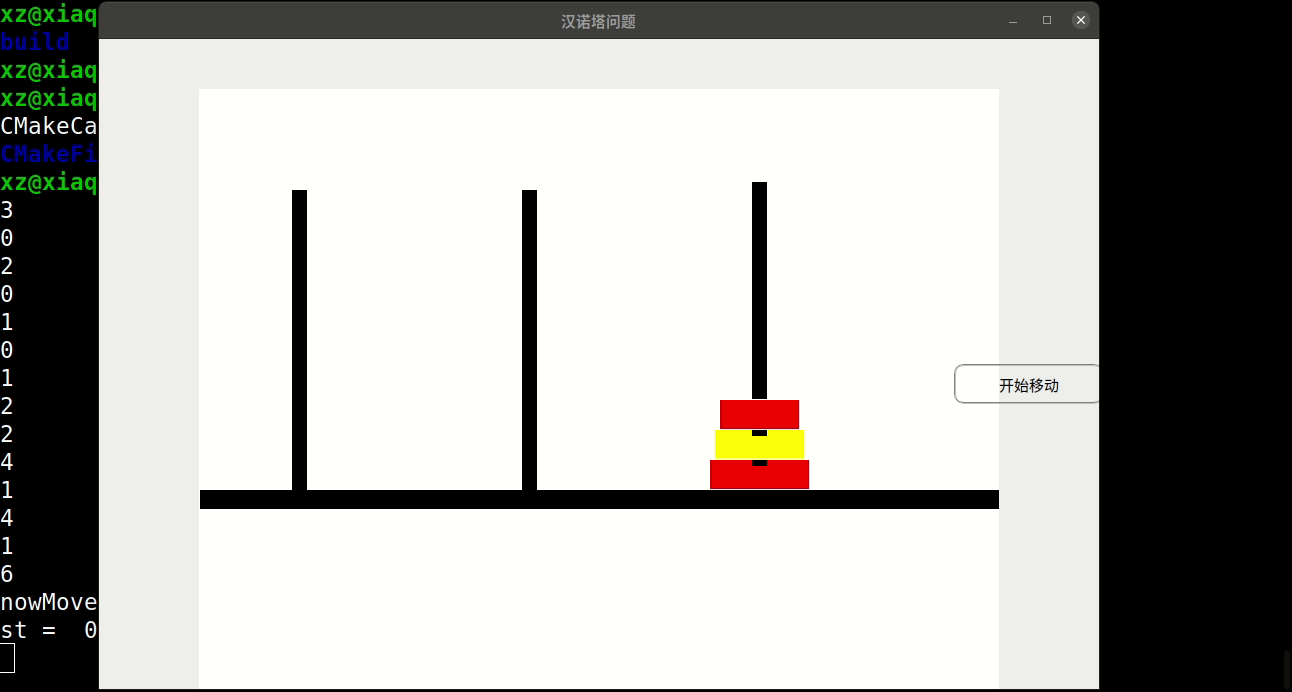
//ex22. 哈哈塔与汉诺塔类似。碟子从 1~n编号 ; 奇数号碟子是红色,偶数号碟子是黄色。碟子
//最初在 1 号塔,从项到底按照 1 ~ n堆放。碟子要移到2号塔,任何时候,同色的碟子不
//能上下挨着。碟子的最后次序和最初次序相同。
//1 ) 编写一个程序,把碟子从 1 号塔移到 2 号塔,可以用 3 号塔作为中转站。
//2 ) 你的程序需要碟子移动多少次?
int main()
{
string str1("(a*(b+c)+d)()");
string str2("(a*(b+c)+d)(");
string str3("(a*[(b+c)+d])");
string str4("(a*[(b+c)+d]){}");
cout<<str1<<endl;
printMatchedPairs(str1);
cout<<str2<<endl;
printMatchedPairs(str2);
cout<<str3<<endl;
printMatchedPairs(str3);
cout<<str4<<endl;
printMatchedPairs(str4);
cout<<unmatchedParen(str1)<<endl;
cout<<unmatchedParen(str2)<<endl;
printMatchedParentsNoStack(str1);
printMatchedPairs2(str3);
printMatchedPairs3(str4);
towersOfHanoi(3,1,2,3);
return 0;
}
测试输出
xz@xiaqiu:~/study/algorithm/c++/1/build$ ./test
(a*(b+c)+d)()
matched '(' and ')' found at 3 7
0 10
11 12
(a*(b+c)+d)(
No match for left parentheis at 11
matched '(' and ')' found at 3 7
0 10
(a*[(b+c)+d])
matched '(' and ')' found at 4 8
0 12
(a*[(b+c)+d]){}
matched '(' and ')' found at 4 8
0 12
1
0
(a* b+c +d)()
a* b+c +d ()
a* b+c +d
matched '(' and ')' found at (3,7)(0,10)(11,12)
unmatched '(' and ']' found at (0,11],both of them will be dropped
unmatched ) found at 12
matched ' '(/[' and ')/]' found at '(4,8)
unmatched '(' and '}' found at (0,11},both of them will be dropped
unmatched ) found at 12
matched ' '{(/[' and ')/]}' found at '(4,8) [3,11] {13,14}
Move top disk from tower 1 to top of tower 2
Move top disk from tower 1 to top of tower 3
Move top disk from tower 2 to top of tower 3
Move top disk from tower 1 to top of tower 2
Move top disk from tower 3 to top of tower 1
Move top disk from tower 3 to top of tower 2
Move top disk from tower 1 to top of tower 2
xz@xiaqiu:~/study/algorithm/c++/1/build$
main.cpp
//ex21. 编写程序中的 showState 方法,假设输出设备是计算机屏幕。如果必要,可以给类
//arrayStack 增加方法,使其能够方便地访问塔上的碟子。需要添加时间延迟,以防显示太
//快而看不清。不同的碟子用不同的颜色显示。
#include "hanoi.h"
#include hanoi.h
#ifndef HANOI_H
#define HANOI_H
#include hanoi.cpp
#include "hanoi.h"
#include