图神经网络及其在知识图谱的应用
一 应用领域
道路交通,动态预测
自动驾驶,无人机场景
化学,医疗等场景
物理模型相关
二 图基本模块定义
V Vertex点
E Edge 边(向量)
U Global 图 (例如:全局向量)
无论事多么复杂,我们利用图神经网络的目的就是整合特征
有向图 出度,入度
无向图 度 Degree
邻接矩阵
子图:所有边和点都在原图中
连通图:对于一个无向图,如果任何的节点i能够通过一些边到达节点j,则称之为连通图
连通分量:无向图G的一个极大联通子图陈伟G的一个联通分量(或连通分支)。连通图只有一个连通分量,即其自身;非连通的无向图有多个连通分量。
有向图连通性
强连通图:强连通图(Strongly Connected Graph)是指在有向图G中,如果对于每一对vi、vj,vi≠vj,从vi到vj和从vj到vi都存在路径,则称G是强连通图。有向图中的极大强连通子图称做有向图的强连通分量。
弱连通图:将有向图的所有的有向边替换为无向边,所得到的图称为原图的基图。如果一个有向图的基图是连通图,则有向图是弱连通图。
最短路径:在一个带权有向图中,从某一顶点到另一顶点可能有很多条路径,最短路径即权值之和最小的那条路径。
图直径:图论中, 图的直径是指任意两个顶点间距离的最大值.(距离是两个点之间的所有路的长度的最小值) 所有最短路径中的最大值
度中心性
度中心性= ![]() =度/总节点-1
=度/总节点-1
特征向量中心性Eigenvector Centrality
一个节点的重要性既取决于其邻居节点的数量(即该节点的度),也取决于其邻居节点的重要性。
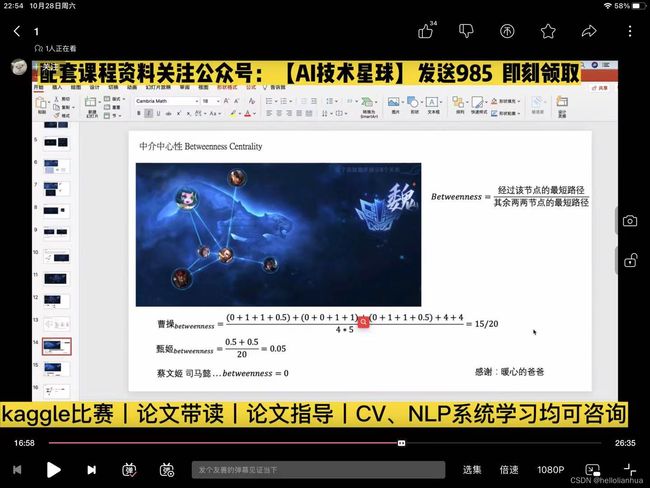
中介中心性Betweenness Centrality
Betweenness=经过该节点的最短路径/其余两两节点的最短路径
连接中心性 Closeness
PageRank
阻尼系数
import numpy as np
import pandas as pd
import networkx as nx
edges=pd.DataFrame()
#edges['sources']代表起始节点
edges['sources']=[1,1,1,2,2,3,3,4,4,5,5,5]
#edges['targets']代表终止节点
edges['targets']=[2,4,5,3,1,2,5,1,5,1,3,4]
#权值
edges['weights']=[1,1,1,1,1,1,1,1,1,1,1,1]
#具体解释为
# 1节点指向2节点权重为1
# 1节点指向4节点权重为1
# 1节点指向5节点权重为1
#定义图
G=nx.from_pandas_edgelist(edges,source='sources',target='targets',edge_attr='weights')
#degree
print(nx.degree(G))
#连通分量
print(list(nx.connected_components(G)))
#图直径
print(nx.diameter(G))
#度中心性
print(nx.degree_centrality(G))
#特征向量中心性
print(nx.eigenvector_centrality(G))
#betweenness
print(nx.betweenness_centrality(G))
#closeness
print(nx.closeness_centrality(G))
#pagerank
print(nx.pagerank(G))
#HITS
print(nx.hits(G))
结果
[(1, 3), (2, 2), (4, 2), (5, 3), (3, 2)]
[{1, 2, 3, 4, 5}]
2
{1: 0.75, 2: 0.5, 4: 0.5, 5: 0.75, 3: 0.5}
{1: 0.5298988890761731, 2: 0.35775191431708964, 4: 0.4271316779596084, 5: 0.5298988890761731, 3: 0.35775191431708964}
{1: 0.25, 2: 0.08333333333333333, 4: 0.0, 5: 0.25, 3: 0.08333333333333333}
{1: 0.8, 2: 0.6666666666666666, 4: 0.6666666666666666, 5: 0.8, 3: 0.6666666666666666}
{1: 0.24369622576677996, 2: 0.17225629712058638, 4: 0.16809495422526693, 5: 0.2436962257667799, 3: 0.17225629712058638}
({1: 0.24059715195481507, 2: 0.1624345647450478, 4: 0.19393656660027417, 5: 0.2405971519548151, 3: 0.1624345647450478}, {1: 0.2405971522393837, 2: 0.1624345646565165, 4: 0.19393656620819955, 5: 0.2405971522393837, 3: 0.1624345646565165})三 邻接矩阵
图像可以作为邻居矩阵 ,A表示邻居之间的关系
GNN(A,X)
文本数据也可以表示图的形式,零阶矩阵表示连接关系
Graphs ->are ->all ->around ->us
| Graphs | are | all | around | us | |
|---|---|---|---|---|---|
| Graphs | 1 | ||||
| are | 1 | ||||
| all | 1 | ||||
| around | 1 | ||||
| us |
GNN要求所有图的格式是一样的,考虑GCN
四 Graph embedding图嵌入
结合第2章的代码可以知道表示图,节点数和边数决定了维度。
4.1 DeepWalk(无向图)
简化了节点的长度
DeepWalk给出的方法是使用随机游走(RandomWalk)的方式在图中进行节点采样。
RandomWalk是一种可重复访问已访问节点的深度优先遍历算法。给定当前访问起始节点,从其邻居中随机采样节点作为下一个访问节点,重复此过程,直到访问序列长度满足预设条件。
获取足够数量的节点访问序列后,使用skip-gram model 进行向量学习。
【Graph Embedding】DeepWalk:算法原理,实现和应用 - 知乎 (zhihu.com)
4.2 Line(有向图)
大规模的图上,表示节点之间的结构信息。
一阶:局部的结构信息 (连接的节点很相似)
二阶:节点的邻居。共享邻居的节点可能是相似的 (不连接的节点A和B,但是A和B分别的连接点很相似,那么A和B也相似)邻居节点多的比较适用此办法
联合概率分布
经验概率分布
4.3 node2Vec
homophily:同质性
structural equivalence:结构等价性
BFS广度优先搜索
DFS深度优先搜索
4.3
四 消息传递
Source,Target
五 多层GCN的作用
GNN也可以有多层
GNN的本质就是更新各部分特征
其中输入是特征,输出也是特征,邻接矩阵也不会变的
(感受野)
六 图卷积GCN
图卷积和卷积有什么不同?
看起来都是利用周围的特征,但是在图中每个点的邻居是不确定的
节点分类,对每个结点进行预测,不同点是否有连接预测
整个图分类,部分图分类等,不同子图是否相似,异常检测等
GCN归根到底还是要完成特征提取操作,只不过输入对象不是固定格式
如何获取特征呢?
通常交给GCN两个东西就行:1.各节点输入特征 2.网络结构图(邻接矩阵)
很多文章,半监督任务也能解决
GCN的基本思想:
争对橙色节点,计算他的特征:平均其邻居特征(包括自身)后传入神经网络
网络层数
这个跟卷积类似,GCN也可以做多层,每一层输入的还是节点特征,然后将当前特征与网络结构图继续传入下层就可以不断算下去
A,D,F
七 知识图谱结合图神经网络的模型模型
7.1 KGCN
KGCN提出于2019年。中心思想就是利用图神经网络的消息传递机制与基本推荐思想结合训练。在做KGCN模型时候,我们就把知识图谱是作为有权图,也就是关系会通过某种方式变为权重,而这个权重可被理解为是该关系影响用户行为的偏好程度。
计算过程
消息传递机制“Embedding”,Embedding 应该是一种映射,就像 Unicode 对应了某一个字符。在某种程度上,就是用来降维的,降维的原理就是矩阵乘法通俗讲解pytorch中nn.Embedding原理及使用 - 简书 (jianshu.com)
lKGCN:推荐系统的知识图谱卷积神经网络(Hongwei et al.,2019) - 知乎
7.2 KGAT
7.3 KGNN-LS
7.4KNI
7.5 AKGE
7.6 KGIN