地震数据去噪

目录

1、经典去噪方法

1）基于滤波的地震数据去噪方法

2）基于稀疏变换的地震数据去

 3）基于模态分解的地震数据去噪方法

4）基于矩阵降秩的地震数据去噪方法

2、深度地震数据去噪方法

3、深度学习全波形反演去噪

4、陆上低信噪反演

1）从数据采集角度

2）从数据预处理角度

3)  从深度网络先验去噪角度

5、如何将陆上去噪方法与我们的深度反演网络结合？

6、参考文献

---

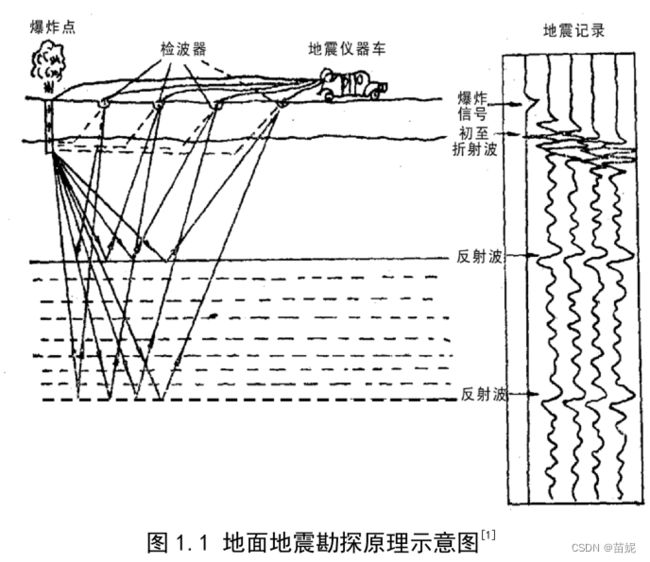
背景：随着油气资源的不断开采，油气地震勘探目标逐渐转向复杂型、隐蔽型、深层和非常规油气藏，这就对地震数据质量有着更高的要求。受复杂自然环境等因素的影响，野外采集到的地震数据不可避免地会受到噪声的干扰，进而影响地下结构成像和地震资料的解释。因此压制地震数据中的噪声，提高地震数据的信噪比，在地震数据处理领域有着极为重要的意义。

噪声分类：在地震勘探中，根据噪声传播规律的不同，通常将噪声分为：相干噪声和不相干噪声这两大类。相干噪声一般包括面波、折射波、多次波等，这是一类具有特定频率和特定视速度的噪声。而不相干噪声没有特定频率和特定传播方向，通常会在地震记录上形成杂乱无章的干扰。不相干噪声通常等同随机噪声。由于噪声会影响后续的地震资料处理，压制地震记录中的噪声是地震数据处理过程中至关重要的一步。

1、经典去噪方法

人们通常根据地震记录中有用信号和噪声之间的特性差异，设计相应的噪声压制算法来实现地震信号去噪。

相干噪声：根据有效信号与相干噪声在频谱、视速度以及到达时间之间的差异，相干噪声通常可以通过各种滤波的方法来压制，例如，截距时间-慢度变换、频率-波数滤波、Karhunen-Loeve 变换、小波域方法等。

非相干噪声：传统的地震数据不相干噪声压制算法通常根据有效信号的相关性和不相干噪声的随机性特性来最大程度地压制噪声，例如频率-空间域滤波算法、中值滤波、奇异值分解、基于 Radon 变换和基于 Curvelet 变换的方法等。

1）基于滤波的地震数据去噪方法

基于滤波的地震数据去噪方法利用有效信号和噪声在时间-空间域、频率域或频率-波数域等中具有较好的分选性，通过设计滤波器来滤去噪声所对应的成分实现去噪的目的。地震中常见的滤波有中值滤波、频域滤波和频率-波数域滤波等，这些滤波方法通常对应着不同的噪声，例如，频域滤波用于去除低频和高频的噪声。另一类滤波方法为预测滤波法，这种方法通过地震信号在时间-空间域和频率域中的可预测性构造出预测滤波器实现噪声去除和信号增强，例如，F-X 反褶积滤波(Gulunay, 1986)和 T-X 预测滤波(Abma and Claerbout, 1995)。基于滤波的去噪方法依赖于有效信号和噪声在某个域中的分选性，当分选性变差时就无法筛选出有效的信号成分。 

2）基于稀疏变换的地震数据去

基于稀疏变换的地震数据去噪是近些年十分流行的方法，这种方法利用有效信号和噪声在变换域中系数幅值差异的特点，通常有效信号对应为大值系数而噪声对应的为小值系数，在变换域中通过硬阈值或软阈值法来滤去噪声所对应的小值系数保留信号相应的大值系数，在通过反变换得到去噪后的信号。基于稀疏变换的去噪效果依赖于稀疏变换对数据表达的稀疏程度，一般认为稀疏程度越高
则去噪的效果要越好，因此多种用于信号分析的数学变换被应用于地震数据的去噪研究中，例如，傅立叶变换(Sacchi et al., 1998; Zhai, 2014)，小波变换(Chen and  Song,  2018;  Gaci,  2014;  Shan  et  al.,  2009),Curvelet 变换(Górszczyk  et  al., 2014;  Lari  and  Gholami,  2014;  张博,  2013),  Radon 变换(Xue  et  al.,  2017)和Seislet 变换(Dalai et al., 2019; Tang et al., 2018)等。基于稀疏变换的方法虽能取得不错的去噪效果，然而由于基函数的特性有时会在去噪结果中带入新的噪声，例如，残留的基函数系数等。另一方面，多尺度多方向的变换通常可以取得比单一尺度和方向变换更好的去噪效果，但多尺度多方向的变换计算量更大以及变换域中的系数高度冗余。

 
3）基于模态分解的地震数据去噪方法

这类方法认为信号是由不同“模态”的子信号叠加而成。若信号中还有噪声，则有效信号的模态要接近于原始信号而噪声信号的模态与原始信号相差较大，因此通过模态分解来分离出信号中的噪，例
如，通过经验模态分解（Empirical Mode Decomposition，EMD）和变分模态分解（Variational  Mode  Decomposition，VMD）对地震数据中的随机噪声进行衰减(Chen, 2016; Liu et al., 2017; Yu and Ma, 2018; Zhou and Zhu, 2019)。模态分解方法依据数据本身在时空域中的特征来进行分解而不需要通过基函数， 但 EMD在分解的过程中基本模态分量的个数不能人为设定。VMD 虽可以人为设定基本模态数，但当 VMD 分解过多时信号则会不连续。 

4）基于矩阵降秩的地震数据去噪方法

基于矩阵降秩的地震数据去噪方法(Anvari et al., 2019b, 2019a; Huang et al., 2016; Li et al., 2020)是根据数据中的噪声会增加数据在频率切片 Hankel 矩阵的秩这一特征，通过降低频率切片 Hankel 矩阵的秩来得到矩阵的近似，从而实现去噪的目的。通过对频率切片 Hankel 矩阵进行降秩然后沿降秩后的对角线做平均处理。因此，基于矩阵降秩的去噪方法也是比较适用于二维等低维地震数据，当处理三维、四维或五维地震数据时的计算量和数据量都将是较大的。

 几种常用地震去噪算法详解：

(1) 中值滤波 
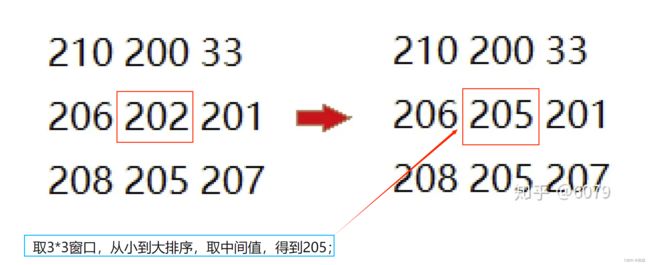
中值滤波是一种经典的非线性滤波方法；该方法基于统计排序理论利用地震资料中某点临域采样点的中值来替代该点的真实值，从而缩小邻域中采样点的值与真实值的差距，最终压制孤立的噪声点，原理如下图所示。中值滤波操作流程简单，消噪效果接近于一个具有平滑功能的低通滤波器。相比线性滤波方法，它可以较好地保留地震资料的边缘信息，但是中值滤波会导致地震资料中高频成分的丢失，影响整个地震资料的分辨率。

(2) F-X 反褶积 
     F-X 反褶积是实际地震勘探中常用的随机噪声压制方法，该方法可以显著增强同相轴的连续性。在地震记录中，有效信号的相干性较强可以被预测，而随机噪声相干性较弱、难以预测。F-X 反褶积利用这一差异预测近似双曲线的同相轴信息，进而实现有效信号和噪声的完整剥离。但是 F-X 反褶积存在两方面的缺陷；其一，F-X 反褶积只能压制随机噪声，在增强信号的同时也可能增强相干噪声，进而导致有效信号的波形畸变以及一些虚假同相轴的出现，降低了地震资料的分辨率和保真度；其二，在复杂地质条件下，同相轴难以满足局部线性，而这正是 F-X 滤波应用的前提条件，因此 F-X 反褶积难以满足一些复杂地震资料的消噪要求。

以下图片参考自地震数据处理第三章：反褶积 

反褶积理想情况下是求解反射系数，但实际的得到的结果是大地滤波器、接收滤波器和相干噪声的综合系统冲击响应。

尽管这些传统的方法在过去几十年取得了不错的效果，但仍然存在一定的局限性，例如，预测速度慢，模型需要反复试验参数（依赖先验信息）；在噪声干扰大或者是地震数据结构复杂的情况下，降噪表现并不令人满意，容易导致有用信号能量的损失或噪声残留。在实际的地震数据去噪问题中，去除噪声及保护细节信息往往是一对矛盾体。对低信噪比或具有复杂结构的地震数据，如何在有效地压制噪声的同时，尽可能的避免有用信号的损失，并且不产生伪吉布斯现象（振铃效应），是地震数据处理领域亟需解决的核心问题之一，有待研究人员们继续研究。

2、深度地震数据去噪方法

由于深度学习方法不需要数据满足特定的先验条件，例如，无空间假频、稀疏性和低秩性等，因此在地震数据处理中也得到了一些初步的应用研究。

可参考：基于深度学习的复杂陆地地震数据噪声压制方法研究_董新桐

3、深度学习全波形反演去噪

4、陆上低信噪反演

例如在通常情况下，面波被认定为干扰波，但是面波的传播运动学以及动力学特征也包含了丰富的
浅层地下介质信息，因此也有专门基于面波的勘探方法。

面波(地滚波)在震源激发后沿着地面与空气之间的分界面进行传播。面波的传播速度相对固定，持续时间长，垂直方向能量衰减快、水平方向能量衰减慢。面波在整个地震记录中呈现为一个近似三角形的形状，振幅较大，有时甚至将有效信号完全截断。 

1）从数据采集角度

针对塔里木盆地缝洞型碳酸盐岩储层，为了得到更高的信噪比和分辨率的串珠成像和更加清晰的属性特征，采用单点高密度地震勘探技术，基本没有假频信息，有利于信噪分离和保幅去噪处理，基于面波反演的压噪技术、稳健地表一致性反褶积技术、ＯＶＴ域处理技术等，从而更加有利于提高最终处理成果质量[3]。

2）从数据预处理角度

针对东濮凹陷砂泥岩薄互储层，进行了叠前地震反演的储层表征，通过自主编程实现了倾角扫描去噪提高叠前 CRP 道集信噪比算法以及道集校平处理，实现了稀疏脉冲法提频处理算法，结合井控提高分辨率技术有效提高了地震资料的频宽，为后续反演提供了较好的基础资料[4]。 

3)  从深度网络先验去噪角度

即插即用先验（PnP）[7]和去噪正则化（RED）[8]是通过利用预训练的深度网络作为先验来成像逆问题的两种最新方法。与传统的正则化子不同，PnP和RED寻求使用去噪引擎来构造正则化子。一些优秀的去噪器，如块匹配和三维滤波器（BM3D）[9]、非局部均值[10]和去噪CNN（DnCNN）[11]，已被采用，并在各种成像应用中表现出出色的性能[12]，[13]。

由于其固有性质，PnP和RED可以避免对正则化子进行微分，从而使该子问题的计算负担在大多数情况下几乎可以忽略不计。PnP的动机是近端算子与去噪运算的数学等价性，因此该方法仅限于近端算法[14]。相反，RED是基于图像自适应拉普拉斯算子的形式提出的，该算子从图像本身构造有用的先验，可以应用于任何通用梯度下降算法，其中梯度包括与数据保真度和正则化项相关的两个项。RED这一优势使RED在选择优化方式时更加灵活。PnP和RED也被用于处理FWI。Aghamary等人[15]提出了两种基于PnP的算法，其中包括牛顿型近似算法，以解决波场重建反演问题。Anagaw和Sachi[16]应用改进的TV构建了一个基于RED的正则化子，然后将其与多尺度频率反演相结合，以验证其有效性。

1) 即插即用PnP正则化不需要显式正则化函数来表示模型的先验信息。利用TV（Total Variation）、BM3D（Block matching and 3D filtering）、FFDNet（Fast and Flexible Denoising convolutional neural network）去噪器，提出了一种基于交替方向乘法器（ADMM）方法的迭代正则化算法。TV正则化子和BM3D正则化子的结合可以利用反问题解的稀疏性和非局部相似性[5]。

2）使用即插即用块匹配（BM3D）正则化求解 FWI ，该算法自适应地确定经验先验，而无需任何优化公式，并且表现出 更快的收敛速度[15]。 

3）针对盐模型的反演问题，提出了一种灵活的无监督学习FWI框架，其中去噪正则化RED为学习梯度提供动力。为了进一步缓解局部极小问题，将Wasserstein距离作为数据域中的一种度量。集成波动方程的物理约束和深度卷积神经网络（CNN）的模型先验，证明在自由表面情况下处理高对比度介质反演任务的有效性。非常适合于地质结构难以使用传统正则化子进行估计的地震成像问题[6]。

4) 二次正则化方法通常用来稳定逆问题，但不能充分保留边缘和尖锐的不连续性。正则化去噪（RED）的框架，通过一个图像去噪引擎，解决高对比度模型中的 FWI 问题，并且其数值实现和平衡参数选择简单。

5、如何将陆上去噪方法与我们的深度反演网络结合？

深度学习方法具有特征快速提取、自主学习、快速求解最优解、精准拟合复杂非线性映射等诸多优点。地震资料中有效信号通常会排列为近似双曲线的形状，具有较强的纹理特性，地震资料可以被视为一种更加复杂的含噪图像。因此我们可以尝试利用 CNN 来建立从含噪地震数据到有效信号的非线性复杂映射关系。此外，CNN 是通过学习海量数据的内在特征信息，进而构建映射关系，因此训练后基于 CNN 的去噪模型可以智能化处理“海量”地震资料，而无需手动参数调节。

基于上述优势，CNN 具有较强潜力完成现代地震勘探中的噪声压制和有效信号恢复的任务。针对“弱信号、强复杂噪声”的地震资料消噪问题，根据实际地球物理问题，构建基于 CNN 的智能降噪网络，建立针对地震资料的智能消噪系，为后期反演、成像以及解释等工作打下坚实的基础。

1）去噪网络（预处理）+  DL-FWI网络 

2）DL-FWI网络 + 正则化去噪器（PnP/RED）

3）多任务DL-FWI网络 （用多任务去替代正则化）

6、参考文献

[1] 基于非局部自相似性和低秩近理论的地震数据去噪方法研究

[2] 基于深度学习的地震数据去噪和重建方法的研究

[3] 碳酸盐岩储层单点高密度采集三维地震勘探实例

[4] 基于叠前地震反演的储层表征技术研究

[5] 2023_Journal of Geophysics and Engineering_An Efficient Plug-and-Play Regularization Method for Full Waveform Inversion

[6] 2023_IEEE_Wasserstein_Distance-Based_Full-Waveform_Inversion_With_a_Regularizer_Powered_by_Learned_Gradient

[7] S. V . V enkatakrishnan, C. A. Bouman, and B. Wohlberg, “Plug-and-play priors for model based reconstruction,” in Proc. IEEE Global Conf.Signal Inf. Process., Dec. 2013, pp. 945–948.
[8] Y . Romano, M. Elad, and P . Milanfar, “The little engine that could:Regularization by denoising (RED),” SIAM J. Imag. Sci., vol. 10, no. 4, pp. 1804–1844, Oct. 2017.
[9] K. Dabov, A. Foi, V . Katkovnik, and K. Egiazarian, “Image denoising by sparse 3D transform-domain collaborative filtering,” IEEE Trans. Image Process., vol. 16, no. 8, pp. 2080–2095, Aug. 2007.
[10] A. Buades, B. Coll, and J.-M. Morel, “Non-local means denoising,”Image Process. Line, vol. 1, pp. 208–212, Sep. 2011.
[11] K. Zhang, W. Zuo, Y . Chen, D. Meng, and L. Zhang, “Beyond a Gaussian Denoiser: Residual learning of deep CNN for image denoising,”IEEE Trans. Image Process., vol. 26, no. 7, pp. 3142–3155, Jul. 2017.
[12] S. Sreehari et al., “Plug-and-play priors for bright field electron tomography and sparse interpolation,” IEEE Trans. Comput. Imag., vol. 2, no. 4, pp. 408–423, Dec. 2016.
[13] S. H. Chan, X. Wang, and O. A. Elgendy, “Plug-and-play ADMM for image restoration: Fixed-point convergence and applications,” IEEE Trans. Comput. Imag., vol. 3, no. 1, pp. 84–98, Mar. 2016.
[14] N. Parikh and S. Boyd, “Proximal algorithms,” F ound. Trends Optim., vol. 1, no. 3, pp. 127–239, Nov. 2014.
[15] H. S. Aghamiry, A. Gholami, and S. Operto, “Full waveform inversion by proximal Newton method using adaptive regularization,” Geophys. J.Int., vol. 224, no. 1, pp. 169–180, Nov. 2020.
[16] A. Anagaw and M. D. Sacchi, “A regularization by denoising (RED) scheme for 3-D FWI model updates in large-contrast media,” Geophys.J. Int., vol. 229, no. 2, pp. 814–827, Jan. 2022.