李宏毅2023机器学习作业HW02解析和代码分享

ML2023Spring - HW2 相关信息：
课程主页
课程视频
Kaggle link
Sample code
HW02 视频
HW02 PDF
个人完整代码分享: GitHub | GitCode | Gitee

P.S. 即便 kaggle 上的时间已经截止，你仍然可以在上面提交和查看分数。但需要注意的是：在 kaggle 截止日期前你应该选择两个结果进行最后的Private评分。
每年的数据集size和feature并不完全相同，但基本一致，过去的代码仍可用于新一年的 Homework。

任务目标（分类）

• Phoneme Classification 音素分类（识别）
  
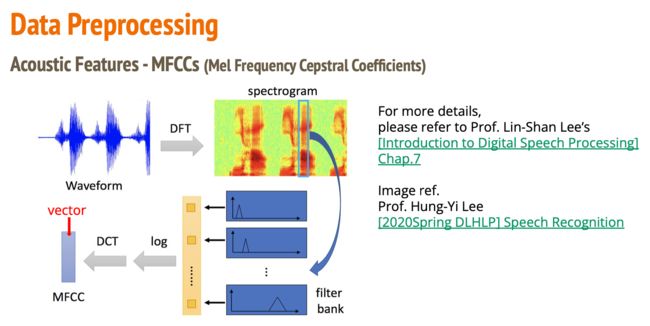
• 训练/测试数据大小：3429/857（2116794/527364 frames）每个 frames 25ms，相邻 frames 间隔 10ms，1s 可以划分出 100 个frames，单个 frames 最后被处理为 39 维的 MFCC (Mel Frequency Cepstral Coefficients)
  
• Label：41，对应 phoneme

Metric

分类精度

数据解析

• train_split.txt: 其中每一行对应一个训练数据，其所对应的文件在feat/train/中
  
• train_labels.txt: 由训练数据和labels组成，格式为: filename labels。其中，label 为 frame 对应的 phoneme
  
• test_split.txt: 其中每一行对应一个训练数据，其所对应的文件在feat/test/中
• feat/train/{id}.pt 和 feat/test/{id}.pt: 音频对应的 MFCC w/ CMVN，维度为39，这些文件可以通过torch.load()直接导入，导入后的shape为(T, 39)。
  

数据来源于 LibriSpeech ASR corpus (subset of train-clean-100): 100小时 “clean” 的演讲训练数据集子集（数据源对应的论文）

数据下载

To use the Kaggle API, sign up for a Kaggle account at https://www.kaggle.com. Then go to the ‘Account’ tab of your user profile (https://www.kaggle.com//account) and select ‘Create API Token’. This will trigger the download of kaggle.json, a file containing your API credentials. Place this file in the location ~/.kaggle/kaggle.json (on Windows in the location C:\Users\\.kaggle\kaggle.json - you can check the exact location, sans drive, with echo %HOMEPATH%). You can define a shell environment variable KAGGLE_CONFIG_DIR to change this location to $KAGGLE_CONFIG_DIR/kaggle.json (on Windows it will be %KAGGLE_CONFIG_DIR%\kaggle.json).

-- [Official Kaggle API]https://github.com/Kaggle/kaggle-api

gdown 的链接总是挂，可以考虑使用 kaggle 的 api，流程非常简单，替换为你自己的用户名，https://www.kaggle.com//account，然后点击 Create New API Token，将下载下来的文件放去应该放的位置：

• Mac 和 Linux 放在 ~/.kaggle
• Windows 放在 C:\Users\\.kaggle

pip install kaggle
# 你需要先在 Kaggle -> Account -> Create New API Token 中下载 kaggle.json
# mv kaggle.json ~/.kaggle/kaggle.json
kaggle competitions download -c ml2023spring-hw2
unzip ml2023spring-hw2

Report

注意到 HW02 有写报告的要求：

1. 实现两个参数量大致相同的模型，(A) 一个深窄的（例如，隐藏层数=6，隐藏维度=1024），(B) 一个浅宽的（例如，隐藏层数=2，隐藏维度=1750）。报告两个模型的训练/验证准确率。
2. 添加dropout层，并分别报告dropout率为(A) 0.25/(B) 0.5/© 0.75时的训练/验证准确率。

1

这个视频片段能够让你更好的了解 Deep Network 和 Shallow network 的差异：Why Deep Learning?

计算神经网络的参数量

先看看如何计算参数。

对于全连接层来说，其单层的参数量为 (输入维度 + 1) * 该层神经元个数。这是因为全连接层的每个神经元都需要一个 权重向量 和一个 偏置值 来计算其输出，权重向量 的长度就是 输入维度，偏置值 是一个标量。

若当前 network 有 hidden_layers 层 hidden layer，其中每层 hidden_layer 有 hidden_dim 维，则有：

$Total\_params=(input\_dim+1)\ast hidden\_dim+(hidden\_dim+1)\ast hidden\_dim\ast (hidden\_layers-1)+(hidden\_dim+1)\ast output\_dim$

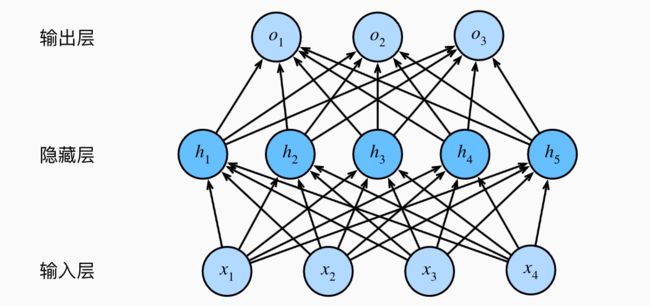
对于一个神经网络来说，其总参数量就是所有全连接层的参数量之和。例如，如果我们有一个神经网络，它有一个输入层（输入维度为 4），一个隐藏层（隐藏层神经元个数为 5），和一个输出层（输出维度为 3），那么它的总参数量就是：

输入层到隐藏层的全连接层：$(4+1)\ast 5=25$
隐藏层到输出层的全连接层：$(5+1)\ast 3=18$
总参数量：$25+18=43$

如下图所示：

这里再举个例子说明：

import torch.nn as nn

input_dim = 8
hidden_dim = 16
hidden_layers = 2
output_dim = 8

# 为了简洁，舍去了 Relu()
network = nn.Sequential(
            nn.Linear(input_dim, hidden_dim),
            # 在函数的调用中，一个 * 表示将一个序列展开为单独的位置参数，这一行代码是列表推导，最终的表现是重复生成多个 hidden layer
            *[nn.Linear(hidden_dim, hidden_dim) for _ in range(hidden_layers-1)], 
            nn.Linear(hidden_dim, output_dim)
        )
# 打印总参数量
total_params = (
    (input_dim+1) * hidden_dim +
    (hidden_dim + 1) * hidden_dim * (hidden_layers - 1) +
    (hidden_dim + 1) * output_dim
)
print(f'Total params: {total_params}')

>> Total params: 552

当然，实际上你可以直接使用 pytorch 中的函数进行打印

total_params = sum(param.numel() for param in network.parameters())
print(f'Total params: {total_params}')

>> Total params: 552

进一步的，如果你想查看各层分别的参数量，你可以使用以下代码

for name, param in network.named_parameters():
    print(name, param.numel())

0.weight 128
0.bias 16
1.weight 256
1.bias 16
2.weight 128
2.bias 8

其中 weight 对应的是权重，bias是偏差。

若concat_nframes = 3, input_dim = 39 * concat_nframe = 117, hidden_layers = 6, hidden_dim = 64, output_dim = 41，则总参数量为31017。

hidden_layers = 2 的情况下，最接近的总参数量为：30890，对应的hidden_dim为113。

但你需要注意的是，concat_nframes 是一个 hyper-parameter，需要根据实际情况调整，所以你也需要相应的对整个网络架构进行改变。

构建总参数量接近的神经网络

已知神经网络的总参数量由下式给出：
$$Total\_params=(input\_dim+1)\ast hidden\_dim+(hidden\_dim+1)\ast hidden\_dim\ast (hidden\_layers-1)+(hidden\_dim+1)\ast output\_dim$$

为了符号简便，做以下简写：

• $i=input\_dim$
• $o=output\_dim$
• $l=hidden\_layers$
• $d=hidden\_dim$

有：
$$Total\_params=(i+1)\ast d+(d+1)\ast d\ast (l-1)+(d+1)\ast o$$
进一步的，将其化成一元二次方程的形式，其中 $d$ 为自变量：
$$Total\_params=(l-1)\ast d^2+(i+o+l)\ast d+o$$

假设 $i,o,l,d$ 均为已知量，现在需要求：在输入输出维度不变的情况下，当 $dest\_hidden\_layers$ 给定时，隐藏层的维数等于多少才能让两个网络的总参数量接近？（$dest$ 代指我们要计算的目标网络）

同样的，做以下简写：

• $l_d=dest\_hidden\_layers$
• $d_d=dest\_hidden\_dim$

则有：
$$dest\_Total\_params=(l_d-1)\ast d_d^2+(i+o+l_d)\ast d_d+o$$

令 $dest\_Total\_params=Total\_params$：
$$\begin{gathered} (l_d-1)\ast d_d^2+(i+o+l_d)\ast d_d+o=(l-1)\ast d^2+(i+o+l)\ast d+o \\ \Downarrow \\ (l_d-1)\ast d_d^2+(i+o+l_d)\ast d_d-(l-1)\ast d^2-(i+o+l)\ast d=0 \end{gathered}$$

这实际上是一个一元二次方程，其中 $d_d$ 为自变量，其余均已知，可当作常数看待。令
$$\begin{gathered} a=l_d-1， \\ b=i+o+l_d， \\ c=-(l-1)\ast d^2-(i+o+l)\ast d \end{gathered}$$
则上式可化成
$$a\ast d_d^2+b\ast d_d+c=0$$
由一元二次方程的求根公式
$$y=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$
有
$$d_d=\frac{-(i+o+l_d)\pm \sqrt{(i+o+l_d{)}^2-4(l_d-l)(-((l-1)\ast d^2-(i+o+l)\ast d))}}{2(l_d-l)}$$

你可以通过调用下方代码中的 get_dest_dim() 获取目标网络隐藏层应该设置的维度。

def get_dest_dim(input_dim, output_dim, hidden_layers, dest_hidden_layers, hidden_dim):
	'''获取目标网络隐藏层的维度（总参数量接近于原网络）'''
    # 计算一元二次方程的系数 a,b,c
    a = dest_hidden_layers - 1  # a = l_d - 1
    b = input_dim + output_dim + dest_hidden_layers  #  b = i + o + l_d
    c = - (hidden_layers - 1) * (hidden_dim ** 2) - (input_dim + output_dim + hidden_layers) * hidden_dim  # c = - (l - 1) * (d ** 2) - (i + o + l) * d
    
    # 计算分子中的平方根部分，即 b^2-4ac
    sqrt_part = (b ** 2) - 4 * a * c
    
    # 计算两个解，一个是加号，一个是减号，即(-b±√(b^2-4ac))/(2a)
    d_d_plus = (-b + sqrt_part**(0.5)) / (2 * a)
    d_d_minus = (-b - sqrt_part**(0.5)) / (2 * a)
    
    # 返回两个解的元组
    return (d_d_plus, d_d_minus)

# 设置你想要的目标网络隐藏层数量
dest_hidden_layers = 2

# 获取对应的维数
dest_hidden_dim, _ = get_dest_dim(input_dim, output_dim, hidden_layers, dest_hidden_layers, hidden_dim)
print(f"若将隐藏层网络层数改为: {dest_hidden_layers}，则维数应当改为: {round(dest_hidden_dim)}",)

2

nn.Dropout(p=) 在激活函数前/后增加都可以。

Sample code 部分解析

Model

这里你可以随意的修改 model 的架构以达到 strong baseline。（原代码中有bug，我进行了修正）

import torch.nn as nn

class BasicBlock(nn.Module):
    def __init__(self, input_dim, output_dim):
        super(BasicBlock, self).__init__()

        # TODO: apply batch normalization and dropout for strong baseline.
        # Reference: https://pytorch.org/docs/stable/generated/torch.nn.BatchNorm1d.html (batch normalization)
        #       https://pytorch.org/docs/stable/generated/torch.nn.Dropout.html (dropout)
        self.block = nn.Sequential(
            nn.Linear(input_dim, output_dim),
            # nn.BatchNorm1d()
            nn.ReLU(),
            # nn.Dropout()
        )

    def forward(self, x):
        x = self.block(x)
        return x


class Classifier(nn.Module):
    def __init__(self, input_dim, output_dim=41, hidden_layers=1, hidden_dim=256):
        super(Classifier, self).__init__()

        self.fc = nn.Sequential(
            BasicBlock(input_dim, hidden_dim),
            # 在函数的调用中，一个 * 表示将一个序列展开为单独的位置参数，这一行代码是列表推导，最终的表现是重复生成多个 hidden layer
            #（原来的整段代码实际上生成了 hidden_layers+1 个隐藏层，所以我修改了一下代码，让其符合定义）
            *[BasicBlock(hidden_dim, hidden_dim) for _ in range(hidden_layers-1)], 
            nn.Linear(hidden_dim, output_dim)
        )

    def forward(self, x):
        x = self.fc(x)
        return x

Hyper-parameters

在这个模块中修改超参数，完成 medium baseline。

# data prarameters
# TODO: change the value of "concat_nframes" for medium baseline
concat_nframes = 3   # 拼接的总数量，应当为奇数，左右各拼接 concat_nframes/2 个 frames（非常重要的参数）
train_ratio = 0.75   # 训练集的比例，

# training parameters
seed = 1213          # random seed
batch_size = 512        # batch size
num_epoch = 10         # the number of training epoch
learning_rate = 1e-4      # learning rate
model_path = './model.ckpt'  # the path where the checkpoint will be saved

# model parameters
# TODO: change the value of "hidden_layers" or "hidden_dim" for medium baseline
input_dim = 39 * concat_nframes  # the input dim of the model, you should not change the value
hidden_layers = 2          # the number of hidden layers
hidden_dim = 64           # the hidden dim

''' 以下是为了完成 report 所添加的代码 '''

# 提前输出模型参数数量，以便调整网络架构
total_params = (
    (input_dim+1) * hidden_dim +
    (hidden_dim + 1) * hidden_dim * (hidden_layers - 1) +
    (hidden_dim + 1) * 41
)
print(f'Total params: {total_params}')
    
def get_dest_dim(input_dim, output_dim, hidden_layers, dest_hidden_layers, hidden_dim):
    '''获取目标网络隐藏层的维度（总参数量接近于原网络）'''
    # 计算一元二次方程的系数 a,b,c
    a = dest_hidden_layers - 1  # a = l_d - 1
    b = input_dim + output_dim + dest_hidden_layers  #  b = i + o + l_d
    c = - (hidden_layers - 1) * (hidden_dim ** 2) - (input_dim + output_dim + hidden_layers) * hidden_dim  # c = - (l - 1) * (d ** 2) - (i + o + l) * d
    
    # 计算分子中的平方根部分，即 b^2-4ac
    sqrt_part = (b ** 2) - 4 * a * c
    
    # 计算两个解，一个是加号，一个是减号，即(-b±√(b^2-4ac))/(2a)
    d_d_plus = (-b + sqrt_part**(0.5)) / (2 * a)
    d_d_minus = (-b - sqrt_part**(0.5)) / (2 * a)
    
    # 返回两个解的元组
    return (d_d_plus, d_d_minus)

# 设置你想要的目标网络隐藏层数量
dest_hidden_layers = 9

# 获取对应的维数
dest_hidden_dim, _ = get_dest_dim(input_dim, 41, hidden_layers, dest_hidden_layers, hidden_dim)
print(f"若将隐藏层网络层数改为: {dest_hidden_layers}，则维数应当改为: {round(dest_hidden_dim)}",)

Baselines

根据作业 PDF 中的提示：

Simple Baseline (0.49798)

• 运行所给的 sample code。

Medium Baseline (0.66440)

• 连接 n 个frames。
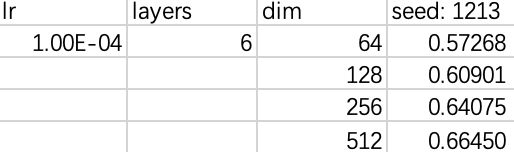
  具体选择多少个 frames 呢？HW02 PDF 中给出的样例是 11 个，查询相关专业知识后有下表：
  
  
  注意到英文中 phoneme 的持续时间都小于 11 个frames（11*25=275ms)。你可以根据专业知识自行选择，比如说你想再联系前后两个 phoneme 的信息来做预测，那设置成 15 也可以，这些由你自己去确定，从实验中获得更好的选择。
• 增加网络的隐藏层。
  下图是我一开始记录的一些实验结果，仅简单的增加了层数和神经元个数便达到了 Medium Baseline（最终记录的是 Kaggle 上的分数），你可以根据自己的情况更进一步的优化它。
  

Strong Baseline (0.74944)

• 在 BasicBlock() 中增加 batchnorm 和 dropout 层。

• 增大 concat_nframes。

  scheduler 的使用实验对比和总结（PyTorch）

  这是关于各 scheduler（ReduceLROnPlateau()，CosineAnnealingLR()，CosineAnnealingWarmRestarts()）使用的对比实验。

  起因是为了在 Kaggle 上跑出更高的成绩，但结果确出乎我的意料，为了工作不白费，我决定将它们的结果重新可视化分享给你们。我一开始没有过多的修改初始配置，这篇文章的目的仅仅是为了给你展现不同 scheduler 下的学习率变化以及对实验结果的影响（片面的）。

  时间原因我仅在这个数据集上跑了对比实验。

  原本是想贴个链接的，想了想还是放在这方便查看。

  开始实验

  为了对比，每个 scheduler 都跑了 300 个epoch，可能不多，但也能看出些端倪。

  这里贴一下我的其他参数，如果不需要做这个 HW，可以跳过这段往下看，并不影响。

  跑 300 个 epoch 是因为在这个参数的设置（请勿模仿）下，大概到 300 就没有什么波动了。

  """dropout(p=0.25)"""
  
  concat_nframes = 15   # the number of frames to concat with, n must be odd (total 2k+1 = n frames)
  train_ratio = 0.95   # the ratio of data used for training, the rest will be used for validation
  
  # training parameters
  seed = 1213          # random seed
  batch_size = 512        # batch size
  num_epoch = 300         # the number of training epoch
  learning_rate =  5e-4     # learning rate
  
  hidden_layers = 6          # the number of hidden layers
  hidden_dim = 512         # the hidden dim
  

  最初，我增加了一个自动调整 learning_rate 的 scheduler，选择的是 torch.optim.lr_scheduler 中的 ReduceLROnPlateau()。

  ReduceLROnPlateau()

  先介绍一下参数方便理解：

  torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer, mode=‘min’, factor=0.1, patience=10, threshold=0.0001, threshold_mode=‘rel’, cooldown=0, min_lr=0, eps=1e-08, verbose=False)

  • optimizer (Optimizer) ：指定需要对哪个优化器对象进行学习率调整。
  • mode (str)：指标的模式。可以是“min”或“max”。如果是“min”，那么当指标停止降低时将调整学习率；如果是“max”，那么当指标停止升高时将调整学习率。
  • factor (float)：学习率缩小的因子。新学习率=旧学习率 * factor。注意，factor 不能大于1。
  • patience (int)：如果指标没有改善，则等待多少个epoch来调整学习率。
  • threshold (float)：指标的变化量阈值，如果小于此值，则将其视为没有改进。
  • threshold_mode (str)：判断阈值的模式。可以是“rel”或“abs”。如果是“rel”，动态阈值等于最优值乘以(1+threshold)（在’max’模式下）或最优值乘以(1-threshold)（在’min’模式下）。在’abs’模式下，动态阈值等于最优值加上threshold（在’max’模式下）或最优值减去threshold（在’min’模式下）。
  • cooldown (int)：表示在减小学习率之后等待几个epoch才能再次减小学习率。
  • min_lr (float or list)：学习率的下限。
  • eps (float)：表示应用于学习率的最小衰减量。如果新旧学习率之间的差异小于eps，则更新会被忽略。
  • verbose (bool)：如果为True，则在调整学习率时打印更新的消息。

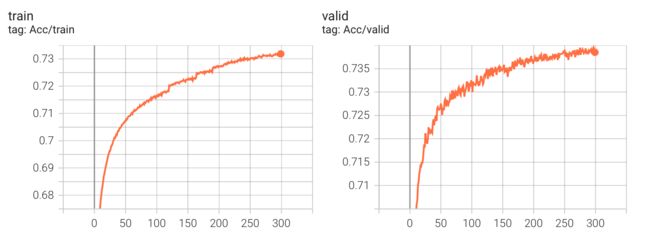
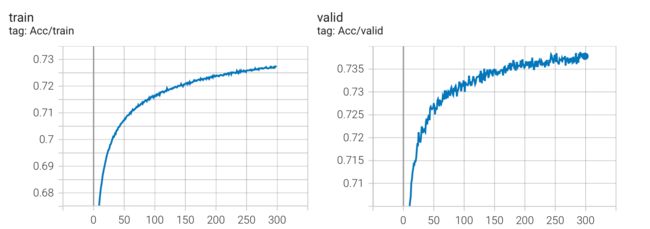
  optimizer = torch.optim.Adam(model.parameters(), lr=5e-4)	# 假设初始学习率为 5e-4
  scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer, mode='max', factor=0.8, patience=10, threshold=0.001)  # 如果 10 个 epoch 后都没有提升，lr *= factor
  
  for epoch in range(num_epoch):
      train(...)				# 训练模型
      validate(...)			# 验证模型
      scheduler.step(metric)	# 根据 metric 更新学习率
  

  学习率变化曲线

  

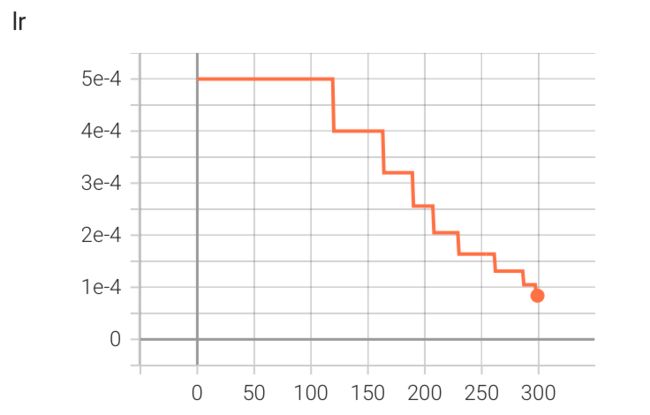
  实验数据

  

  Kaggle 分数: 0.74427

  最初选择 ReduceLROnPlateau() 的原因是基于一个设想的较乐观的情况：只要慢慢减少学习率一定会收敛到优秀的解。

  当时发现了好几种scheduler，但看到根据 epoch 变化 learing rate 的 scheduler（比如 StepLR，ExponentialLR），觉得完全不如根据实验结果动态变化的 ReduceLROnPlateau 便没有进行选择。

  看到这里你应该仅仅对 ReduceLROnPlateau() 有了简单的认识，不妨继续往下看，看看实验对比。

  在 acc 卡住后，我试图去寻找其他的 scheduler，看能不能让 learning rate 在中途变大跳出一些区域后再变小，然后发现还有周期性变化的 scheduler（比如 CosineAnnealingLR，CyclicLR），于是，我尝试修改成 CosineAnnealingLR()。

  CosineAnnealingLR()

  torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max, eta_min=0, last_epoch=- 1, verbose=False)

  • optimizer (Optimizer) ：指定需要对哪个优化器对象进行学习率调整。
  • T_max (int): 表示半个周期的长度。例如，如果T_max=10，则学习率在第0个epoch时为最大值，在第0到第10个epoch之间以余弦函数形式逐渐减小，在第10个epoch时达到最小值，在第11到第20个epoch之间以余弦函数形式逐渐增大，在第20个epoch时回到最大值。
  • eta_min (float): 表示学习率的最小值，在学习率下降到这个值之后，就不再下降了。默认为0。
  • last_epoch (int): 表示上一次更新学习率的epoch索引。默认为-1，表示还没有开始训练。这个参数用于恢复训练时使用，可以将其设置为已经训练的epoch数减 1。
  • verbose (bool)：如果为True，则在调整学习率时打印更新的消息。

  optimizer = torch.optim.Adam(model.parameters(), lr=5e-4)	# 假设初始学习率为 5e-4
  scheduler = torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max=10, eta_min=1e-7)
  
  for epoch in range(num_epoch):
      train(...)				# 训练模型
      validate(...)			# 验证模型
      scheduler.step()		# 更新学习率
  

  学习率变化曲线

  

  实验数据

  

  Kaggle 分数: 0.74391（没有提升）

  这个 scheduler 中的 learning rate 变化曲线与余弦函数一致，但观察发现，CosineAnnealLR 的周期性变化似乎让收敛的过程变得曲折（多次实验效果都类似）。

  观察 acc 和 lr 的变化：每一次 lr 逐步上升都会让 acc 下降。于是我想着有没有一种 scheduler，让 lr 跳过逐步上升的过程，于是找到了 CosineAnnealingWarmRestarts，这个 scheduler 会让 learning rate 在周期的最后瞬间上升 ，这个概念在李宏毅老师过去的视频中也有说到，即：warm restart。

  CosineAnnealingWarmRestarts()

  torch.optim.lr_scheduler.``CosineAnnealingWarmRestarts(optimizer, T_0, T_mult=1, eta_min=0, last_epoch=- 1, verbose=False)

  • optimizer (Optimizer) ：指定需要对哪个优化器对象进行学习率调整。
  • T_0 (int): 表示第一次restart的epoch，即在T_0个epoch后，学习率将回到最高点，重新开始下降。默认值为10。
  • T_mult (float): 表示每次restart之后T_0的值将乘以T_mult。默认值为1。
  • eta_min (float): 表示学习率的最小值，在学习率下降到这个值之后，就不再下降了。默认为0。
  • last_epoch (int): 表示上一次更新学习率的epoch索引。默认为-1，表示还没有开始训练。这个参数用于恢复训练时使用，可以将其设置为已经训练的epoch数减 1。
  • verbose (bool)：如果为True，则在调整学习率时打印更新的消息

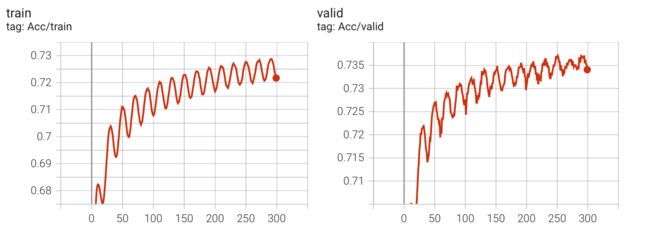
  optimizer = torch.optim.Adam(model.parameters(), lr=5e-4)	# 假设初始学习率为 5e-4
  scheduler = torch.optim.lr_scheduler.CosineAnnealingWarmRestarts(optimizer, T_0=10, T_mult=1, eta_min=1e-7)
  
  for epoch in range(num_epoch):
      train(...)				# 训练模型
      validate(...)			# 验证模型
      scheduler.step()		# 更新学习率
  

  学习率变化曲线

  

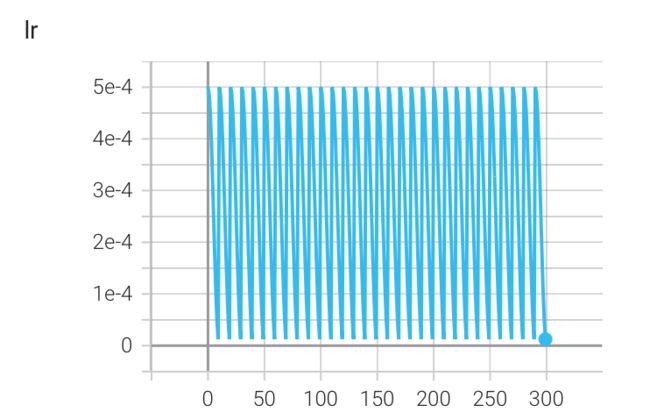
  实验结果

  

  Kaggle 分数: 0.74328（没有提升）

  我以为实验结果会变得更好，发现并没有，无论哪种 scheduler，最终的结果都差不多（epoch = 300），这可能是我初始lr设置的太大（5e-4）的原因？

  虽然我产生了修改学习率的想法，但我还想尝试一下另一种修改方式，因为我发现 CosineAnnealLR 参数中 T_max 指代的是半个周期的长度，而 CosineAnnealingWarmRestarts 参数中的 T_0 指代的是一个周期长度，我将二者都设置成了 10，这使得 CosineAnnealingWarmRestarts 在300个epoch中有30个周期，是 CosineAnnealLR 的两倍，我或许应该将 T_0 设置为 2*T_max 来进行最终的对比实验。

  

  T_0 *= 2

  学习率变化曲线

  

  实验结果

  

  Kaggle 分数: 0.74403（没有提升）

  看起来，各个 scheduler 最终的表现似乎没有区别？我决定跑一个没有scheduler的版本（是的，我一开始默认的觉得加上scheduler一定会让实验变得更好，但发现似乎并不是这样，最起码在当前的配置下不是（有可能是batchnorm的原因？））。

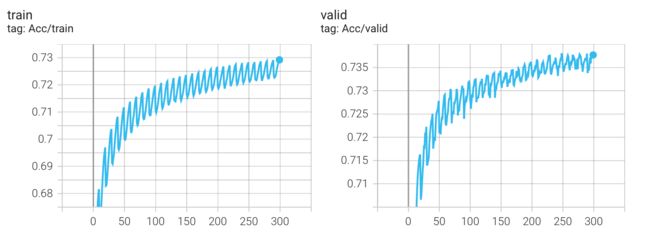
  no scheduler

  学习率变化曲线

  

  实验结果

  

  Kaggle 分数: 0.74408

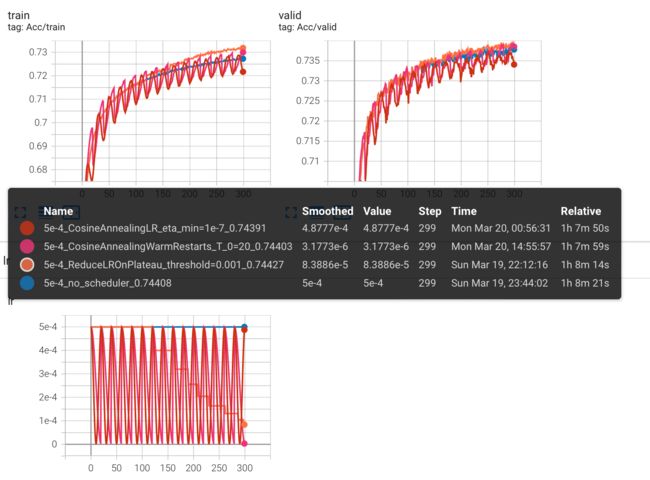
  实验结果对比

  

  评价是：花里胡哨，没有区别（HW02 下）。真要用的话， ReduceLROnPlateau() 就够了，有时可以减少训练时间。

  现在，我决定根据一个现象去改变 lr 的初始值：从输出中，观察到在所有周期中，每次 lr=2.5e-4 和 1.72e-4 的时候上升幅度最大，于是我将 lr 设置成 2.5e-4 重新跑了所有的实验。

  修改 lr=2.5e-4，重新实验

  实验结果对比

  

  可以看到，Kaggle 分数没有提升。

  下图是 lr = 5e-4 和 lr=2.5e-4 的 CosineAnnealingWarmRestarts 对比结果：

  

  原以为会有很大的变化，比如在 lr 的最高点处 acc 不会降低这么多，发现并没有，甚至可以说是一模一样，这其中一定有什么我还不了解的东西在发挥作用。

  总结

  scheduler 真的没有作用吗？不尽然，这很大程度上取决于你现在的损失函数面和参数配置，使用 scheduler 往往可以更快的收敛。下图是对比：

  

  而且，如果你经常性的重新导入模型，那么使用带 last_epoch 参数的 scheduler 会更方便。

  同样的，如果你的模型花费时间很长，也可以通过像 StepLR() 这类的 scheduler 让 lr 在每一轮次变化。

  但相对于盲目的使用一些可能提高 metric 的函数，你更应该在预处理数据上下功夫：

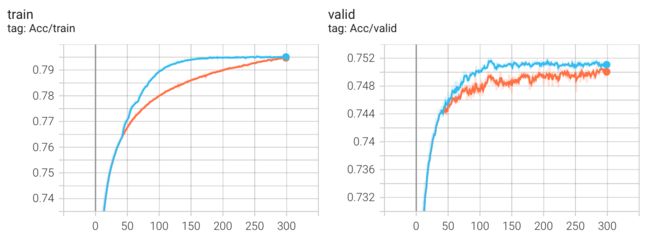
  • 跑完这个对比实验后，我增加了输入的维度，让数据在一开始拥有更多的信息（对应到 HW02 就是：将 concat_nframes 从 15 增加到了 21，使得在网络可以更多的考虑到相邻的音素），仅仅改变这一条，Kaggle 的分数便超过了 strong baseline，达到了 0.75623。
    
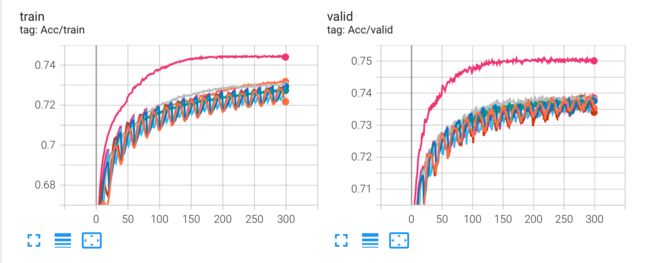
  • 进一步的，dropout 其实不应设置成 25，通过观察可以发现：没有 dropout 的时候，训练集很容易便能达到 90+ 的准确率，当然，这是过拟合了。但 p=25 时，acc 一直上不去又何尝不是欠拟合呢？基于这个想法，我在 p=25/15 下做了对比，下图是大致的实验结果（使用了 ReduceLROnPlateau()）：
    
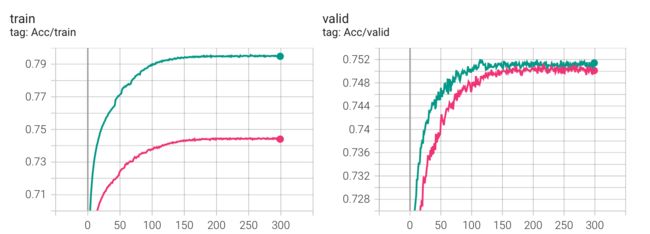
    发现这使得 acc 比之前更快的抵达了 strong baseline，至于刚刚所想的欠拟合，好像没有体现出来 : )

  P.S. epoch 设置成 300 完全是为了跑对比实验，做 HW 的时候不要设这么大，浪费时间。
  实验局限在一个可能不好的参数配置，也局限在单独的 optimizer 之下，仅向大家展示片面的的结果 : )

  好了，以上就是关于一些 scheduler 使用的实验对比和总结，希望对你有所帮助～

Boss Baseline (0.83017)

• 使用 RNN。

为什么我的模型能跑，但效果很差：错误处理了dataloader返回的数据

PyTorch中 rnn() 有一个参数是batch_first，这个参数如果设置成 True，那么意味着 input 的 shape 从 (seq_len, batch_size, input_size) => (batch_size, seq_len, input_size)，同样的，此时如果要取最后一个状态，代码从 x[-1] 改成 x[:, -1]。

dataloader 返回的数据 shape 是 (batch_size, input_dim)，所以，features = features.to(device) 应该修改成 features = features.view(-1, concat_nframes, 39).to(device)，如果你和我一开始一样：因为知道 rnn 的 input.shape=(seq_len, batch_size, input_size)，所以不使用 batch_first=True，但不熟悉 dataloader 返回的 shape格式。那么，你很有可能会使用 features = features.shape(concat_nframes, -1, 39).to(device)，这样可以训练，但效果奇差，而且:) 不会报错。

你需要格外注意上面这点，必须正确处理 feature 的维度，可以不用设置 batch_first=True，因为这样顶多就是把 self.rnn(x) 改成 self.rnn(x.permute(1, 0, 2))。

我需要花一周时间去应对组会的 Deadline，所以会断更一下，结束后我会继续更新。

个人完整代码分享: GitHub | GitCode | Gitee

参考链接

1. What’s the difference between reshape and view in pytorch?