递推的简单入门

递推的简单入门

第一篇博文的观看量日益增加，我感到很开心。能把我所学到的东西分享给大家，并得到大家的认可，是我一直写下去的动力，愿你我能共同进步，加油！！！

递推法的基本思想
递推就是利用问题本身所具有的一种递推关系来求解问题的一种方法，是指从已知的初始条件出发，依据某种递推关系，逐次推出所要计算的中间结果和最终结果。
对于初始条件：
1.要么在问题的本身已经给定
2.要么通过对问题的分析化简后来确定。

• 递推的本质
  把一个复杂的计算过程转化为一个简单的过程的多次计算。

• 可递推求解的问题特点
  1 问题可以划分成多个状态。
  2 除了初始状态外，其他各状态都可以用固定的关系式来求解。

• 递推的应用
  1 常用于按照一定的规律来计算序列中的指定项。
  2 递推关系式不会直接给出。（通过分析问题的状态，再使用归纳法来找出递推的关系式）

• 递推的方法
  1，正向顺推：从已知的条件出发，向着所求问题前进，最终与所求的问题联立。
  2，反向逆推：从所求的问题出发，向着已知条件靠拢，最后与已知条件联系起来。（从所求的问题出发一步步还原出答案）

下面我通过一些问题的讲解来带领大家进一步感受递推

• 养兔子问题

Description
一对成熟的兔子每天能且只能产下一对小兔子，每次都生一公一母，每只小兔子的成熟期是1天，小兔子出生后隔一天才能再生小兔子。第一天某人领养了一对成熟的兔子，一公一母，请问第N天以后，他将会得到多少对兔子。

Input
输入为一个整数n(1 ≤ n ≤ 90)。

Output
对应输出第n天有几对兔子(假设没有兔子死亡现象，而且是一夫一妻制)。

Sample
Input
2
Output
2
Hint
数据类型可以用64位整数:long long

通过对问题的分析，我们可以得到：
首先，我们分析一下问题的状态，第n天的兔子肯定由已经成熟的兔子，和刚出生的兔子组成，可以把这看成两种状态。接下来，我们通过已经找到的状态来找问题的递推关系，（总的来说，我们要求某一天的兔子个数，要依靠前几天的兔子个数来判定（反向逆推），现在我们假设第n天的兔子个数我们都已知，这样我们就可以放心的求解问题了 ）
第一步，求第n天的成兔个数，根据我们对题意的理解我们可以得到，第n-1天的兔子到第n天都可以变成成兔（不考虑兔子再生的情况，因为刚生下来的兔子都是小兔），就可以当作是一种继承。
第二步，求第n天的小兔个数，我们发现通过第n-1 天的兔子数求不方便（因为，我们知到小兔都是由成兔产下的，第n-1天的小兔在第n天不能产下小兔，我们也不知道第n-1天的小兔数量），由小兔隔一天可以生下小兔，我们可以联想到用第n-2天的兔子来求解，事实证明也是对的，因为第n-2 天的小兔在第n天时都可以产下小兔，所以第n天的小兔的数量就是前两天兔子的数量。
这样我们就可以列出递推关系式，设第n天的兔子数量为f[n] ，
f[n]=f[n-1]+f[n-2];
这恰好是斐波那契数列。下面给出代码。

#include 

using namespace std;
const int M=1e3+10;

int main()
{
	int n;
	long long int f[M];
	cin>>n;
	f[1]=1;
	f[2]=2;
	for(int i=3;i<=n;i++)
	{
		f[i]=f[i-1]+f[i-2];
	}
	cout<<f[n];
	return 0;
 } 

ps:有些人可能还有一些疑问：为什么第n-1天的成兔生下的小兔会不会对结果产生影响呢？
当时我想了比较长的时间，可能是我比较笨吧
原因：想想第n-1天的成兔来源，不正是由第n-2天的成兔的继承和小兔的生长而来的吗，也就是第n-2天所有的兔子数量。（其实是反复运用了第一步）

• 骨牌铺方格问题

Description
在2×n的一个长方形方格中,用一个1× 2的骨牌铺满方格,输入n ,输出铺放方案的总数. 例如n=3时,为2× 3方格，骨牌的铺放方案有三种,如下图：

Input
输入包含一个整数n,表示该测试实例的长方形方格的规格是2×n (0< n<=50)。

Output
输出铺放方案的总数。

Sample
Input
3
Output
3
这个问题呢我相信会有人乍一看非常懵，没错正是本人 ，由于这个题的方法有点抽象，对于初次接触到的新人来说呢，理解起来会有点别扭，我就稍微点一下思路，随着以后大家对于递推的理解进一步加深，再来看这一道题目就非常的容易。
还是使用反向逆推的方法：

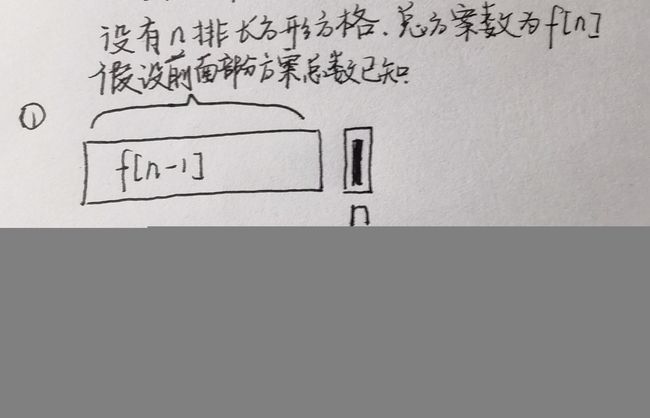
我们可以看到最后面只有两种情况，竖着排一个和横着排两个，继续往前推还是这两种情况，所以状态确定了之后就可以确定递推关系式：
f[n]=f[n-1]+f[n-2];
下面给出代码。

#include 

using namespace std;
int M=1e3+10;

int main()
{
	int n;
	long long int f[M];
	cin>>n;
	f[1]=1;
	f[2]=2;
	for(int i=3;i<=n;i++)
	{
		f[i]=f[i-1]+f[i-2];
	}
	cout<<f[n];
	return 0;
 } 

和上一个相同

• 三国佚事——巴蜀之危

Description
话说天下大势，分久必合，合久必分。。。却道那魏蜀吴三国鼎力之时，多少英雄豪杰以热血谱写那千古之绝唱。古人诚不我欺，确是应了那句“一将功成万骨枯”。
是夜，明月高悬。诸葛丞相轻摇羽扇，一脸愁苦。原来是日前蜀国战事吃紧，丞相彻夜未眠，奋笔急书，于每个烽火台写下安排书信。可想，这战事多变，丞相运筹 帷幄，给诸多烽火台定下不同计策，却也实属不易。
谁成想这送信小厮竟投靠曹操，给诸葛丞相暗中使坏。这小厮将每封书信都投错了烽火台，居然没有一封是对的。不多时小厮便被抓住，前后之事却也明朗。这可急坏了诸葛丞相，这书信传错，势必会让蜀军自乱阵脚，不攻自破啊! 诸葛丞相现在想知道被这小厮一乱，这书信传错共有多少种情况。

Input
输入一个正数n，代表丞相共写了n（1 <= n <= 20）封书信。

Output
输出书信传错的情况数。

Sample
Input
3
Output
2
这个题是一个全部错排的题，很典型，希望大家能够好好理解一下。
还是利用反向逆推：

设第n封信对应的烽火台是正确的，前边的n-1封信假设知道错排的方案数为f[n-1]，我们要的是全部错排，只要将第n封信与前边n-1封信的任意一封交换就能实现全部错排，所以一种情况的方案数为(n-1)*f[n-1];

我们继续在前边n-1个错排中再找出一个p书信和正确的烽火台对应，剩下的错排方案数就为f[n-2]，这时我们发现只需要将p和n交换即可实现完全错排，由于p是从n-1中任意找的所以，这一种情况的方案数为(n-1)f[n-2];
我们分析的两种情况都对结果有贡献，且正好包含了所有的情况，当然这是在我知道答案的前提下做出的判断，在做题时我们需要证明其他情况对与结果没有贡献。

那我们就再从剩余的错排中找出一个正确的q，这时我们发现一次交换并不能实现完全错排，所以我们就说剩下的情况对于结果没有贡献了。
所以我们就得出了一个递推关系式：
f[n]=(n-1)(f[n-1]+f[n-2]);
下面给出代码。

#include 

int main()
{
	int n;
	long long int a[22];
	scanf("%d",&n);
	a[1]=0;
	a[2]=1;
	for(int i=3;i<=n;i++)
	{
		a[i]=(i-1)*a[i-1]+(i-1)*a[i-2];
	}
	printf("%lld",a[n]);
	return 0;
 } 

下面给一个资料，大家可以更清晰的了解错位排列

• 王小二切饼

Description
王小二自夸刀工不错，有人放一张大的煎饼在砧板上，问他：“饼不许离开砧板，切n(1<=n<=100)刀最多能分成多少块？”
Input
输入切的刀数n。
Output
输出为切n刀最多切的饼的块数。
Sample
Input
100
Output
5051
这个题终于用到了正向顺推：

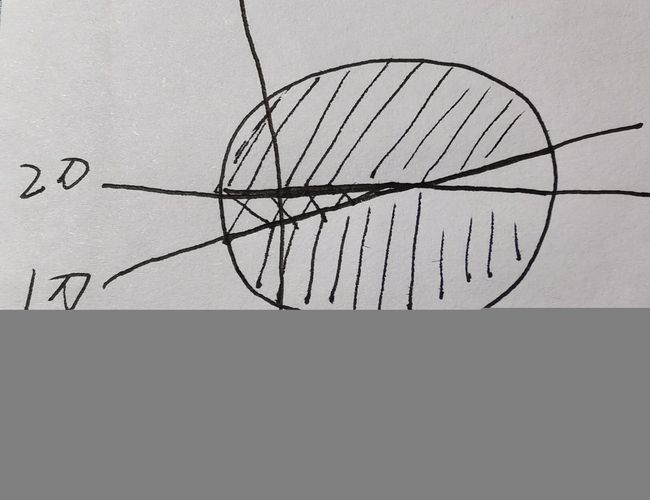
第一刀我们把饼分为两部分，第二刀我们把饼分为四部分，前两部很难看出什么，第三刀，因为我们要求饼的最多块数，所以第三刀应该尽量与前几刀相交，我们从图中可以看到，第三刀，把图中标的每一个用符号标识的部分分为了两部分，增加了3块，以后也不难发现，每次增加的块数就是切饼的当前次数，用观察法就可以看出，还有一种数学归纳法可以更严谨的证明，适用于解决复杂的问题（由于本博文讲的主要是入门，便不做介绍）。
经分析，我们得到递推关系式：
f[n]=f[n-1]+n;
下面给出代码：

#include 

int main()
{
	int n;
	long long int a[101];
	scanf("%d",&n);
	a[1]=2;
	a[2]=4;
	for(int i=3;i<=n;i++)
	{
		a[i]=a[i-1]+i;
	}
	printf("%lld",a[n]);
	return 0;
}

• 马拦过河卒问题

Description
棋盘上A点有一个过河卒，需要走到目标B点。卒行走的规则：可以向下、或者向右。同时在棋盘上C点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。棋盘用坐标表示，A点（0，0）、B点（n，m）（n，m为不超过15的整数），同样马的位置坐标是需要给出的。现在要求你计算出卒从A点能够到达B点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。
Input
一行四个数据，用空格分隔，分别表示B点的坐标和马的坐标。
Output
一个数据，表示所有的路径条数。
Sample
Input
6 6 3 3
Output
6
这个题呢，确实比较难，但其实明白了其中的道理，也是能慢慢做出来的。用文字解释也不是很清楚，我就先稍微介绍一下，之后老师讲的时候会更加的明白
首先，我们的思路时本来没有马的阻拦时，就走通一条路，就在最后的结果加一，所以我们面对这个题只需要判断是不是遇到马就行了。具体的东西会在下面的代码解释。
至于递推方程由卒走的特点可知：
f[i][j]=f[i-1][j]+f[i][j-1];
具体代码如下

#include 
#include 
#include 
#include 
#define ll long long
using namespace std;
const int N = 1e2+10;
int n,m,a,b;
long long int f[N][N];
int l[] = {-2,-1,1,2,2,1,-1,-2,0};  //八个方位，还有不要忘记中间的那一个
int r[] = {-1,-2,-2,-1,1,2,2,1,0};
bool judge(int idx,int idy)    //bool函数就是一个只能返回true和false的函数其实用int型的函数来返回1或0也可
{

	for(int i=0;i<=8;i++)
	{	
	    int x=l[i]+a,y=r[i]+b;      //让马的坐标回到“正确位置”
		if(x==idx&&y==idy) return true;
	}
	return false;
}
int main()
{
	scanf("%d %d %d %d",&n,&m,&a,&b);
	f[0][0]=1;
	for(int i=0;i<=n;i++){
		for(int j=0;j<=m;j++){
			if(j==0&&i==0) continue;   
			if(judge(i,j)) f[i][j]=0;
			else if(j==0) f[i][j]=f[i-1][j];  //注意边界情况的判断
			else if(i==0) f[i][j]=f[i][j-1];
			else f[i][j]=f[i-1][j]+f[i][j-1];
		}
	}
	printf("%lld\n",f[n][m]);
	return 0;
}

• 结语
  递推的一些入门知识就在这里了，欢迎大家来“享用”，因为我还不大会使用电脑作图，暂时用手绘来代替，大家多多见谅，如果大家发现什么问题，或有什么建议请在评论区留言，我永远和你们同在！fighting!