前端常用算法总结js

1.冒泡排序

对相邻两个元素进行比较，若前一个大于后一个，则将两个元素调换位置，执行完一次完整的外层for循环就会确定一个最大元素到数组的末尾，若排序的数组长度为n，那么第一次确定一个最大数需要比较n-1次，第二次n-2次，所以时间复杂度为 （n-1） + （n-2）+ … + 1 推导出表达式n(n - 1 )/2 所以复杂度即为 O(n^2)，但是在最好的情况下只需要执行n-1次

动图展示（图示转载的：http://www.guoyaohua.com）

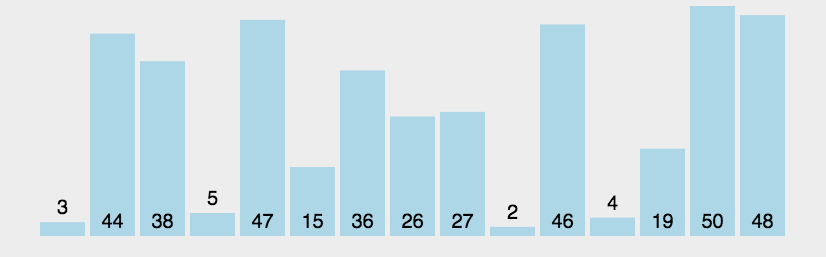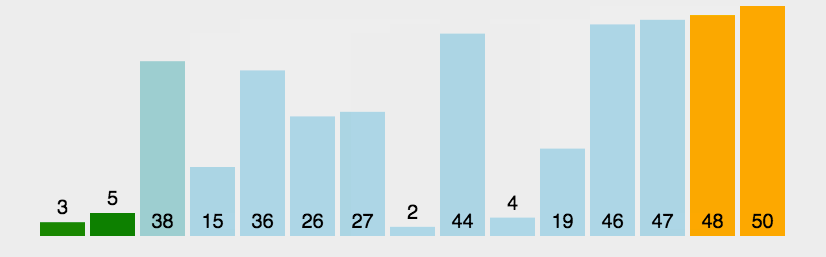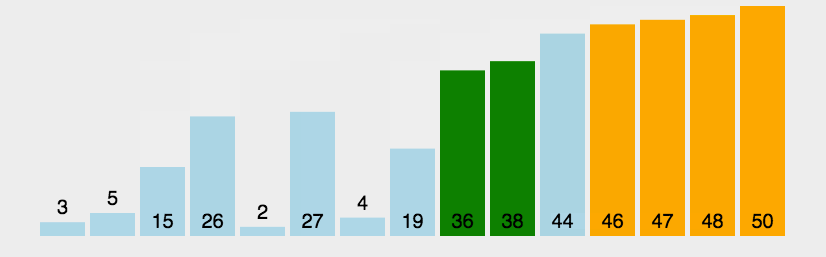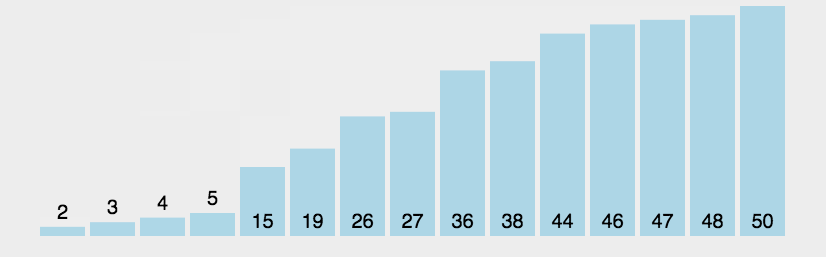
js实现

const arr = [8,342,645,7645,5673,234,63,456,346,54]

/**
 * 冒泡排序
 */
const mpFn = (list) => {
  for(var i = 0; i < list.length - 1; i++) {
    for (var j = 0; j < list.length - 1 - i; j++) {
        if (list[j] > list[j + 1]) {
          var a = list[j]
          list[j] = list[j + 1]
          list[j + 1] = a
        }
    }
  }
}

mpFn(arr)
console.log(arr)

但是上面的这种写法有弊端，也许杂乱的数组排序几次就排好了，他还会继续排序，没必要，可以优化一下

const arr = [8,54,63,234,342,346,456,645,7645,5673]

/**
 * 冒泡排序
 */
const mpFn = (list) => {
  var num = 0
  for(var i = 0; i < list.length - 1; i++) {
    var isOk = true // 是否已经排好了
    for (var j = 0; j < list.length - 1 - i; j++) {
      ++num
      if (list[j] > list[j + 1]) { // 进了这个循环就代表没排好
        var a = list[j]
        list[j] = list[j + 1]
        list[j + 1] = a
        isOk = false
      }
    }
    if (isOk) { // 如果排好了跳出循环
      break
    }
  }
  console.log(num, '执行次数')
}


mpFn(arr)
console.log(arr)

2.选择排序

对要排序的数组进行循环 每次循环找出该数组的最大（最小）值，将这个值从数组中剪切出来，让后在对应的位置插入，那么第一次确定一个最小值（最大值）需要比较n-1次，第二次n-2次，所以时间复杂度为 （n-1） + （n-2）+ … + 1 推导出表达式n(n - 1 )/2 所以复杂度即为 O(n^2)，不管怎么样也要执行n(n - 1 )/2次

动图展示（图示转载的：http://www.guoyaohua.com）

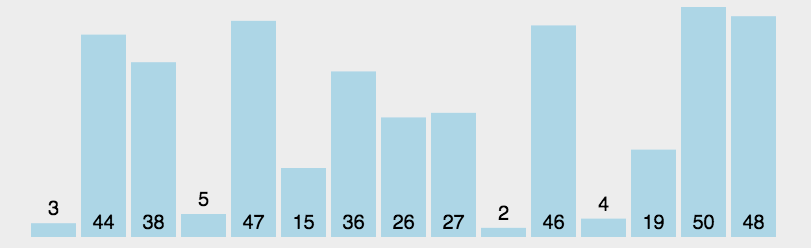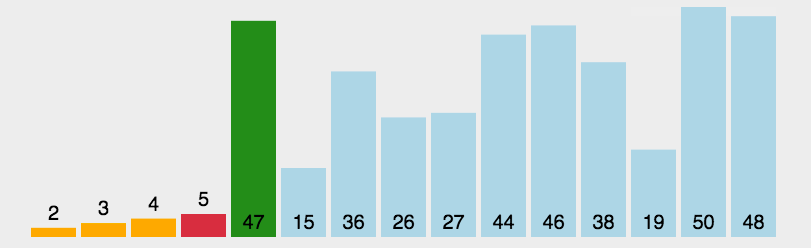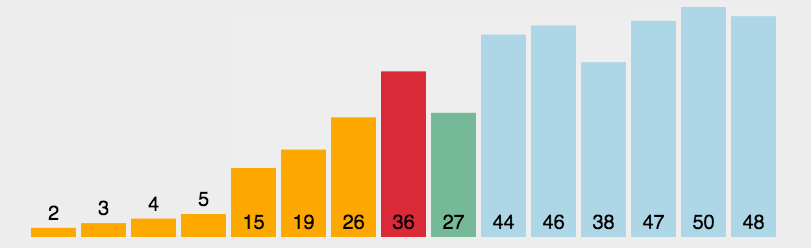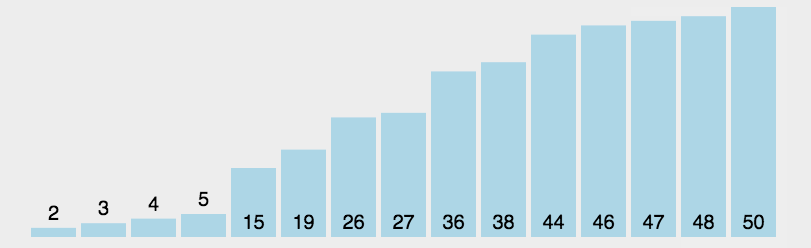
js代码实现

const arr = [63,234,7645,342,346,456,54,645,8,5673]

/**
 * 选择排序
 */
const xzFn = (list) => {
  var num = 0
  for(var i = 0; i < list.length - 1; i++) {
    let minIdx = i
    for (var j = i + 1; j <= list.length - 1; j++) {
      ++num
      if (list[minIdx] > list[j]) {
        minIdx = j
      }
    }
    if (minIdx !== i) {
      const [value]  = list.splice(minIdx, 1)
      list.splice(i, 0, value)
    }
  }
  console.log(num, '执行次数')
}


xzFn(arr)
console.log(arr)

3.插入排序

循环要排序的数组，从第二个元素开始，依次拿当前值去与它前面的值进行比较，如果它刚好满足大于前一个，小于后一个，那么就将它插入其中，或者它比第一个元素还小，那它就插入最前面，那么完成一次比较，第一次需要1，第二次最多需要2次，以此类推1 + 2 + … + n - 1 推导出表达式n(n - 1 )/2 所以复杂度即为 O(n^2),但是在最好的情况下只需要执行n-1次,这种算法理论上更容易比冒泡选择、选择更少的次数

动图展示（图示转载的：http://www.guoyaohua.com）

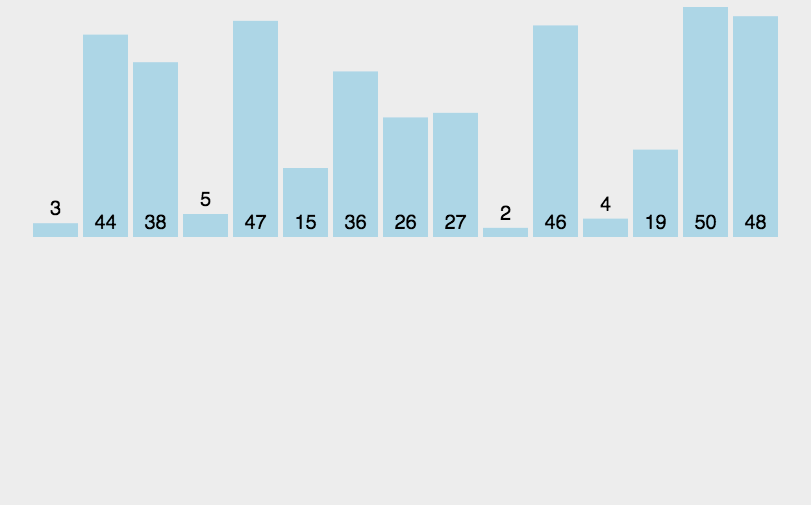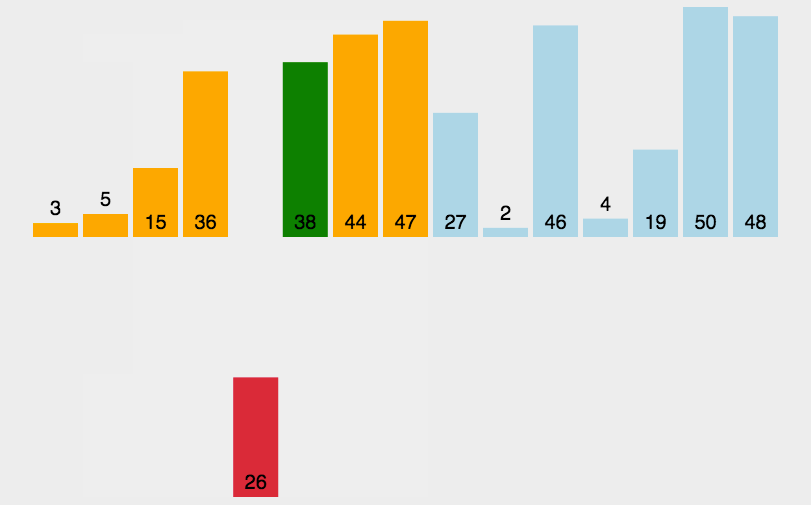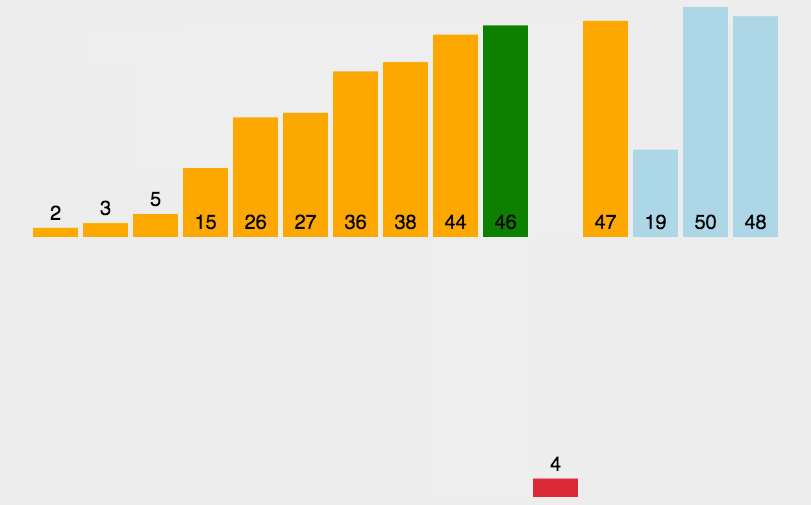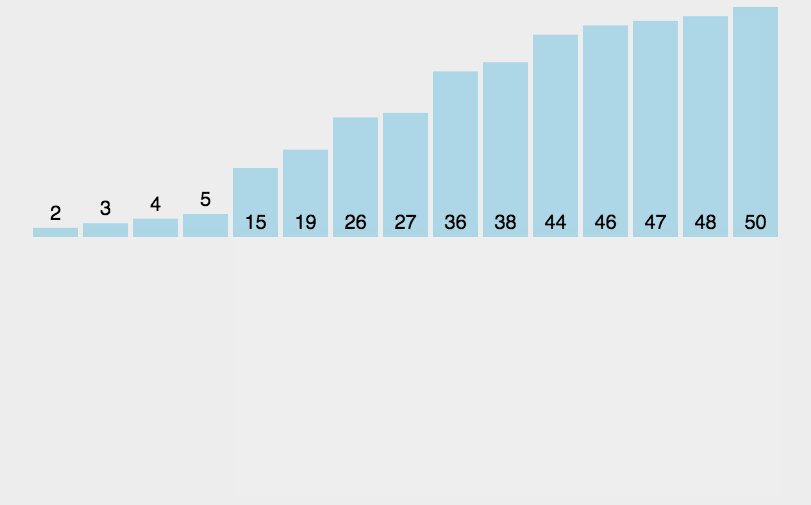
js实现

const arr = [63,234,7645,342,346,456,54,645,8,5673]
/**
 * 插入排序
 */

const crFn = (list) => {
  var num = 0
  for(var i = 1; i <= list.length - 1; i++) {
    let insertIdx = -1
    for (var j = 0; j < i; j++) {
      ++num
      if (j === 0 && list[j] >= list[i]) {
        insertIdx = j
      } else if (j > 0 && list[j-1] <= list[i] && list[i] <= list[j]) {
        insertIdx = j
      }
    }
    if (insertIdx !== -1) {
      const [value]  = list.splice(i, 1)
      list.splice(insertIdx, 0, value)
    }
  }
  console.log(num, '执行次数')
}


crFn(arr)
console.log(arr)

4.快排

将要排序的数组，将数组的第一个元素作为边界，拆分为小于边界的数组和大于等于边界的数组，拆分后的数组再次拆分，也就是递归判断，直到需要拆分的数组长度为1，换句话说就是递归。

动图展示（图示转载的：http://www.guoyaohua.com）

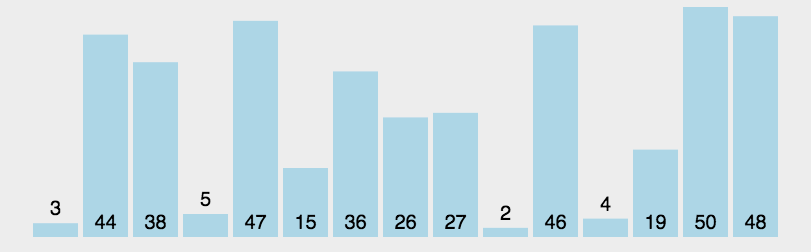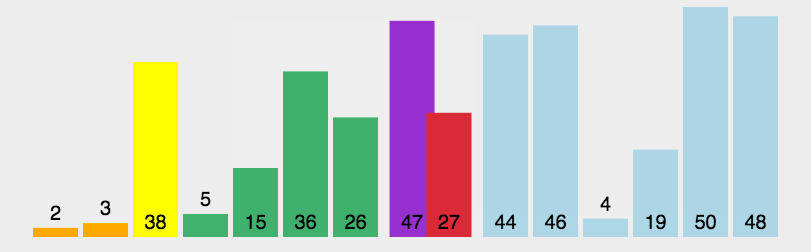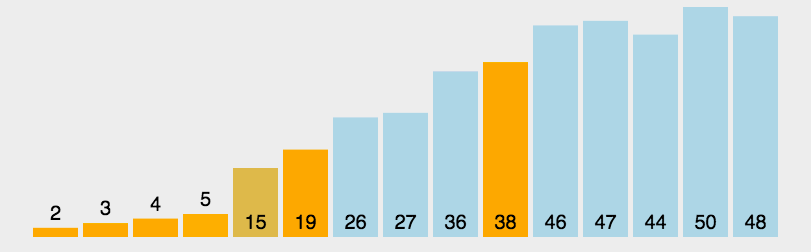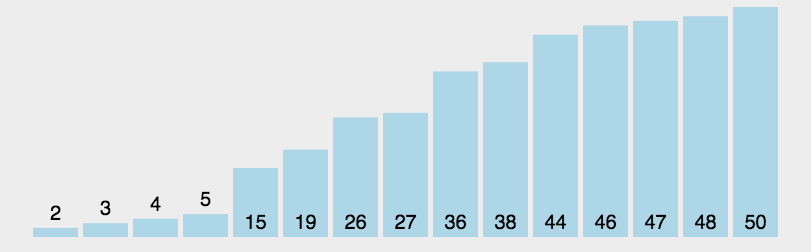
js实现

const arr = [63,234,7645,342,346,456,54,645,8,5673]
let num = 0
/**
 * @info 快排
 */
const kpFn = (list) => {
  console.log(qfFn(list))
  console.log(num, '执行次数')
}

/**
 * @info 将数组切分为两个数组
 */
const qfFn = (list) => {
  if (list.length === 1 || list.length === 0) {
    num++
    return list
  } else {
    const minArr = []
    const maxArr = []
    for (var i = 1; i < list.length; i++) {
      num++
      if (list[0] >= list[i]) {
        minArr.push(list[i])
      } else {
        maxArr.push(list[i])
      }
    }
    return [...qfFn(minArr), list[0], ...qfFn(maxArr)]
  }
}


kpFn(arr)
// console.log(arr)