Apriori算法
Apriori算法是关联规则挖掘算法,也是最经典的算法。
Apriori算法是一种用于挖掘数据集中频繁项集的算法,进而用于生成关联规则。这种算法在数据挖掘、机器学习、市场篮子分析等多个领域都有广泛的应用。
Apriori算法是为了发现事物之间的联系的算法,比如我们熟知的啤酒与尿布故事,某超市在对顾客购物习惯分析时,发现,男性顾客在购买婴儿尿片时,常常会顺便搭配几瓶啤酒来犒劳自己,于是尝试推出了将啤酒和尿布摆在一起的促销手段,最后使得啤酒与尿布销量双双提升。
一. 关联分析概述
关联分析用于发现隐藏在大型数据集中的令人感兴趣的联系 ,所发现的模式通常用关联规则或频繁项集的形式表示。关联分析可以应用于生物信息学、医疗诊断、网页挖掘、科学数据分析等。
选择物品间的关联规则也就是要寻找物品之间的潜在关系。要寻找这种关系,有两步,以超市为例
- 找出频繁一起出现的物品集的集合,我们称之为频繁项集(根据定义,这些项集出现的频繁性至少和预定义的最小支持计数一样)。比如一个超市的频繁项集可能有{{啤酒,尿布},{鸡蛋,牛奶},{香蕉,苹果}}
- 在频繁项集的基础上,使用关联规则算法找出其中物品的关联结果,由频繁项集产生强关联规则(根据定义,这些规则必须满足最小支持度和最小置信度)。
简单点说,就是先找频繁项集,再根据关联规则找关联物品。
为什么要先找频繁项集呢?还是以超市为例,我们找物品关联规则的目的是什么,是为了提高物品的销售额。如果一个物品本身购买的人就不多,那么你再怎么提升,它也不会高到哪去。所以从效率和价值的角度来说,肯定是优先找出那些人们频繁购买的物品的关联物品。
就像在超市买泡面,一桶面不够吃,两桶吃不了,你是不是就想,要不我在顺便买个香肠?还不够!在加个蛋呢?实在不行,再加个鸡腿!
好了,现在你就明白了,泡面、香肠、鸡蛋、鸡腿,这4个商品可能就是关联的,如果超市把这几个放在一起,你在买泡面的时候,是不是就很容易一不小心就多消费了。
关联规则挖掘:关联规则挖掘是数据挖掘中的一个重要分支,其目标是发现在一个数据集中变量间存在的有趣的关联或模式。
例子: 假设在一个零售商的交易数据中,如果客户购买了啤酒,他们也很有可能购买薯片。这里的“啤酒”和“薯片”就形成了一个关联规则。
频繁项集(Frequent Itemset):频繁项集是在数据集中出现次数大于或等于最小支持度(Minimum Support Threshold)的项的集合。满足最小支持度阀值(minsup)的所有项集。
频繁k项集的集合通常记作Lk。
例子: 在超市购物数据中,如果“牛奶”和“面包”这一组合经常一起出现在同一个购物篮里,并且出现的次数超过了最小支持度,那么{"牛奶", "面包"}就是一个频繁项集。
二.关联分析的几个概念
项(Item): 在关联规则挖掘中,项通常指数据集中的一个元素。
例子: 在一个超市的购物篮数据中,"牛奶"、"面包"、"啤酒"等都是单个的项。
项集(Itemset): 是一个项的集合,可以包含0个或多个项。
例子: {"牛奶", "面包"} 和 {"啤酒", "薯片", "面包"} 都是项集。
k-项集:一个项集包含k个项。
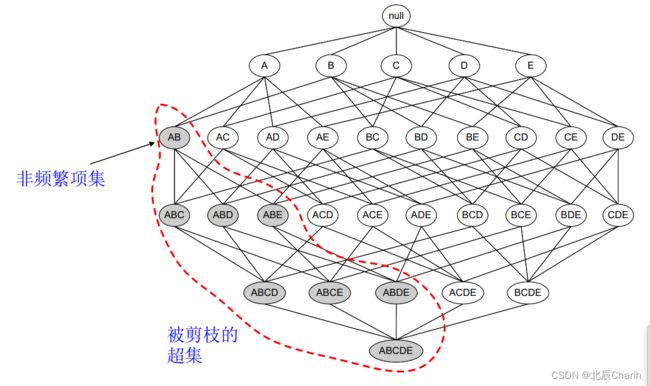
先验原理(Apriori principle):如果一个项集是频繁的,则它的所有非空子集一定也是频繁的。
相反,任何非频繁项集的超集都为非频繁项集。
–这种基于支持度度量修剪指数搜索空间的策略称为基于支持度的剪枝(support-based pruning)
–这种剪枝策略依赖于支持度度量的一个关键性质,即一个项集的支持度决不会超过它的子集的支持度。这个性质也称为支持度度量的反单调性(anti-monotone)。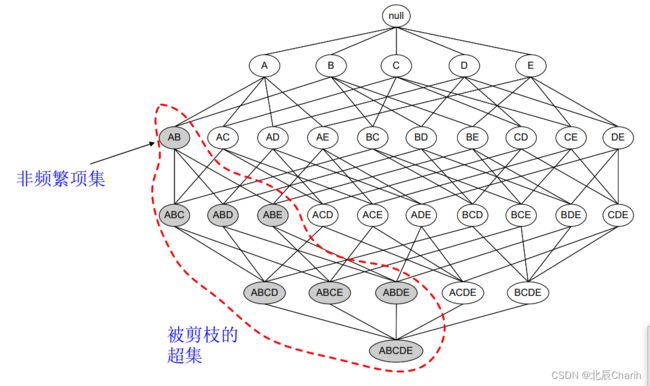
支持度计数(Support count)(σ):包含特定项集的事物个数。
支持度(Support):是某个项集在所有交易中出现的频率。它用于衡量一个项集的普遍性,表示一个项集在整个数据集中出现的频率。包含项集的事务数与总事务数的比值。支持度可以理解为物品当前流行程度。计算方式是:
支持度 = (包含物品A的记录数量) / (总的记录数量)
例子: 如果我们有100笔交易,其中有30笔交易包含了“可乐”,那么“可乐”的支持度就是30%。
如果一共有五个交易,牛奶出现在三个交易中,鸡蛋出现在四个交易中,故而{牛奶}的支持度为3/5。{鸡蛋}的支持度是4/5。牛奶和鸡蛋同时出现的次数是2,故而{牛奶,鸡蛋}的支持度为2/5。
置信度(Confidence):置信度是指如果购买物品A,有较大可能购买物品B。即是在A出现的情况下,B出现的条件概率。计算方式是这样:
置信度( A -> B) = (包含物品A和B的记录数量) / (包含 A 的记录数量)
例子: 如果在包含“牛奶”的所有交易中,有70%的交易也包含了“面包”,那么从“牛奶”到“面包”的置信度就是70%。
若(牛奶,鸡蛋)一起购买的次数是两次,牛奶的购买次数是3次,鸡蛋的购买次数是4次。那么Confidence(牛奶->鸡蛋)的计算方式是Confidence(牛奶->鸡蛋)=2 / 3。
规则的支持度和置信度是规则兴趣度的两种度量。支持度是对关联规则重要性的衡量,置信度
是对关联规则准确度的衡量,支持度说明了这条规则在所有事务中有多大代表性。 显然支持度越大,关联规则越重要。有些关联规则置信度虽然很高,但支持度却很低,说明该关联规则实用的机会很小,因此也不重要。
提升度(Lift):提升度指当销售一个物品时,另一个物品销售率会增加多少。用于衡量事物A和B的出现是否相互独立。计算方式是:
提升度( A -> B) = 置信度( A -> B) / (支持度 A)
例子:上面我们计算了牛奶和鸡蛋的置信度Confidence(牛奶->鸡蛋)=2 / 3。牛奶的支持度Support(牛奶)=3 / 5,那么我们就能计算牛奶和鸡蛋的支持度Lift(牛奶->鸡蛋)=1.11
当提升度(A->B)的值大于1的时候,说明物品A卖得越多,B也会卖得越多。而提升度等于1则意味着产品A和B之间没有关联。最后,提升度小于1那么意味着购买A反而会减少B的销量。
Apriori原理:Apriori原理是Apriori算法的核心,它基于一个简单但重要的观察:一个项集是频繁的,那么它的所有子集也必须是频繁的。
例子: 如果{"牛奶", "面包", "啤酒"}是一个频繁项集,那么{"牛奶", "面包"}、{"牛奶", "啤酒"}和{"面包", "啤酒"}也必须是频繁项集。
Apriori算法的重要性:Apriori算法由于其简单、高效的特性,在数据挖掘中有着广泛的应用。它不仅能用于挖掘数据中的隐藏模式,还能用于诸如产品推荐、用户行为分析、网络安全等多个应用场景。
例子: 在电子商务网站中,Apriori算法可以用于分析用户购买历史数据,进而实现个性化推荐,提升销售额和用户满意度。
应用场景:由于其广泛的用途和灵活性,Apriori算法在以下几个主要领域内有着广泛的应用:
- 市场篮子分析: 了解哪些产品经常被一起购买,以进行有效的产品布局或优惠策略。
- 医疗诊断: 分析病人的历史数据,找出病症和治疗方案之间的关联。
- 网络安全: 通过分析网络日志,找出异常模式,以预防或检测安全威胁。
三、Apriori算法介绍
Apriori的作用是根据物品间的支持度找出物品中的频繁项集。
通过上面我们知道,支持度越高,说明物品越受欢迎。
那么支持度怎么决定呢?这个是我们主观决定的,我们会给Apriori提供一个最小支持度参数,然后Apriori会返回比这个最小支持度高的那些频繁项集。
说到这里,有人可能会发现,既然都知道了支持度的计算公式,那直接遍历所有组合计算它们的支持度不就可以了吗?
是的,没错。我们确实可以通过遍历所有组合就能找出所有频繁项集。但问题是遍历所有组合花的时间太多,效率太低,假设有N个物品,那么一共需要计算2^N-1次。每增加一个物品,数量级是成指数增长。而Apriori就是一种找出频繁项集的高效算法。它的核心就是下面这句话:
某个项集是频繁的,那么它的所有子集也是频繁的。
这句话看起来是没什么用,但是反过来就很有用了。
如果一个项集是 非频繁项集,那么它的所有超集也是非频繁项集。
如图所示,我们发现{A,B}这个项集是非频繁的,那么{A,B}这个项集的超集,{A,B,C},{A,B,D}等等也都是非频繁的,这些就都可以忽略不去计算。
运用Apriori算法的思想,我们就能去掉很多非频繁的项集,大大简化计算量。
四、Apriori算法概述
算法步骤
Apriori算法分为两个步骤:
- 第一步通过迭代,检索出事务数据库中的所有频繁项集,即支持度不低于用户设定的阈值的 项集;
- 第二步利用频繁项集构造出满足用户最小信任度的规则。
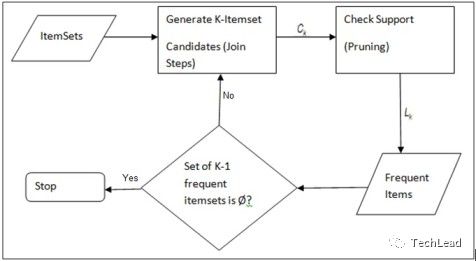
Apriori算法的执行流程主要包含两个步骤:
- 频繁项集生成(Frequent Itemset Generation): 找出满足最小支持度阈值的所有频繁项集。
- 关联规则生成(Association Rule Generation): 从频繁项集中生成高置信度的关联规则。
频繁项集生成
该算法使用一种逐层搜索的迭代方法,即从频 繁1-项集到最长的频繁项集,它每次遍历项集格中的一层,利用k-项集探索(k+1)-项集。
- 扫描数据集,找出所有单一项的支持度,并筛选出满足最小支持度的项。
- 使用满足最小支持度的项生成新的候选项集。
- 计算新生成的候选项集的支持度,并再次筛选。
- 重复上述步骤,直到不能生成新的频繁项集。
例子: 假设有一个购物交易数据集,其中包括5笔交易。第一步是计算所有单一商品(如“牛奶”,“面包”等)在这5笔交易中的出现次数,并筛选出那些出现次数达到最小支持度的商品。
关联规则生成
- 对于每一个频繁项集,生成所有可能的非空子集。
- 对每一条生成的规则 ( A \Rightarrow B ),计算其置信度。
- 如果规则的置信度满足最小置信度要求,则该规则为有效关联规则。
例子: 对于频繁项集 {"牛奶", "面包", "黄油"},可能的规则有 "牛奶, 面包 -> 黄油", "牛奶, 黄油 -> 面包" 等。计算这些规则的置信度,并筛选出满足最小置信度的规则。
优缺点
优点
- 简单易懂: Apriori算法基于直观的原理,并且计算过程简单。
- 可扩展性强: 算法可以应用于大规模的数据集。
缺点
- 计算量大: 在大数据集上,可能需要生成大量的候选项集。
- 多次扫描数据: 算法需要多次扫描数据集以计算项集的支持度,这在数据集很大时可能是低效的。
例子: 在一个包含百万级交易数据的电子商务网站中,使用Apriori算法可能需要消耗大量计算资源和时间。
通过以上的详细描述和例子,我们应该对Apriori算法有了全面而深入的理解。这为我们后续的技术解析和实战应用奠定了基础。
五、Apriori算法实例
让我们在一个非常著名的业务场景市场篮分析的帮助下,尝试并理解 Apriori 算法的工作原理。
这是一个小时内包含六个事务的数据集。每个事务都是 0 和 1 的组合,其中 0 表示不存在某项,而 1 表示其存在。
| 交易编号 | 葡萄酒 | 薯片 | 面包 | 牛奶 |
| 1 | 1 个 | 1 个 | 1 个 | 1 个 |
| 2 | 1 个 | 0 | 1 个 | 1 个 |
| 3 | 0 | 0 | 1 个 | 1 个 |
| 4 | 0 | 1 个 | 0 | 0 |
| 5 | 1 个 | 1 个 | 1 个 | 1 个 |
| 6 | 1 个 | 1 个 | 0 | 1 个 |
我们可以从这种情况下找到多个规则。例如,在葡萄酒,薯条和面包的交易中,如果购买了葡萄酒和薯条,那么客户也会购买面包。
{葡萄酒,薯条} => {面包}
现在我们知道了找出有趣规则的方法,让我们回到示例中。在开始之前,让我们将支持阈值固定为 50%。
步骤 1:创建所有交易中出现的所有项目的频率表
| 项目 | 频率 |
| 葡萄酒 | 4 |
| 薯片 | 4 |
| 面包 | 4 |
| 牛奶 | 5 |
步骤 2:根据支持阈值查找重要项目
支持阈值 = 3
| 项目 | 频率 |
| 葡萄酒 | 4 |
| 薯片 | 4 |
| 面包 | 4 |
| 牛奶 | 5 |
步骤 3:从重要的项目开始,使成对的商品与订单无关
| 项目 | 频率 |
| 葡萄酒,薯条 | 3 |
| 葡萄酒,面包 | 3 |
| 葡萄酒,牛奶 | 4 |
| 薯条,面包 | 2 |
| 薯片,牛奶 | 3 |
| 面包,牛奶 | 4 |
步骤 4:根据支持阈值找到重要项目
| 项目 | 频率 |
| 葡萄酒,牛奶 | 4 |
| 面包,牛奶 | 4 |
第 5 步:根据第 4 步中的重要商品,三件一起购买的商品
| 项目 | 频率 |
| 葡萄酒,面包,牛奶 | 3 |
{酒,面包,牛奶} 是从给定数据中获得的唯一重要项目集。但是在实际场景中,我们将有数十个项目可用来构建规则。然后,我们可能必须制作四对 / 五对项集。
六、Apriori算法实战
用一个简单的例子来用一下Apriori,这里用到的库是mlxtend。
在放代码之前,先介绍下Apriori算法的参数。
def apriori(df, min_support=0.5,
use_colnames=False,
max_len=None)
参数如下:
df:这个不用说,就是我们的数据集。
min_support:给定的最小支持度。
use_colnames:默认False,则返回的物品组合用编号显示,为True的话直接显示物品名称。
max_len:最大物品组合数,默认是None,不做限制。如果只需要计算两个物品组合的话,便将这个值设置为2。OK,接下来就来用一个简单的例子来看看怎么使用Apriori算法找到频繁项集。
import pandas as pd
from mlxtend.preprocessing import TransactionEncoder
from mlxtend.frequent_patterns import apriori
#设置数据集
dataset = [['牛奶','洋葱','肉豆蔻','芸豆','鸡蛋','酸奶'],
['莳萝','洋葱','肉豆蔻','芸豆','鸡蛋','酸奶'],
['牛奶','苹果','芸豆','鸡蛋'],
['牛奶','独角兽','玉米','芸豆','酸奶'],
['玉米','洋葱','洋葱','芸豆','冰淇淋','鸡蛋']]
te = TransactionEncoder()
#进行 one-hot 编码
te_ary = te.fit(records).transform(records)
df = pd.DataFrame(te_ary, columns=te.columns_)
#利用 Apriori 找出频繁项集
freq = apriori(df, min_support=0.05, use_colnames=True)首先,需要先将商品进行one-hot编码,编码后用boolean值表示。所谓ont-hot编码呢,直观来说就是有多少个状态就有多少比特,而且只有一个比特为1,其他全为0的一种码制。比如冰淇淋只存在最后一共交易单中,其他交易中都没出现。那冰淇淋就可以用[0,0,0,0,1]来表示
这里编码后的数据如下:
冰淇淋 洋葱 牛奶 独角兽 玉米 肉豆蔻 芸豆 苹果 莳萝 酸奶 鸡蛋
0 False True True False False True True False False True True
1 False True False False False True True False True True True
2 False False True False False False True True False False True
3 False False True True True False True False False True False
4 True True False False True False True False False False True我们设定的最小支持度是0.6,那么只有支持度大于0.6的物品集合才是频繁项集,最终结果如下:
support itemsets
0 0.6 (洋葱)
1 0.6 (牛奶)
2 1.0 (芸豆)
3 0.6 (酸奶)
4 0.8 (鸡蛋)
5 0.6 (芸豆, 洋葱)
6 0.6 (洋葱, 鸡蛋)
7 0.6 (牛奶, 芸豆)
8 0.6 (酸奶, 芸豆)
9 0.8 (芸豆, 鸡蛋)
10 0.6 (芸豆, 洋葱, 鸡蛋)完整代码:
import pandas as pd
from mlxtend.preprocessing import TransactionEncoder
from mlxtend.frequent_patterns import apriori
# 设置数据集
dataset = [['牛奶','洋葱','肉豆蔻','芸豆','鸡蛋','酸奶'],
['莳萝','洋葱','肉豆蔻','芸豆','鸡蛋','酸奶'],
['牛奶','苹果','芸豆','鸡蛋'],
['牛奶','独角兽','玉米','芸豆','酸奶'],
['玉米','洋葱','洋葱','芸豆','冰淇淋','鸡蛋']]
te = TransactionEncoder()
# 进行 one-hot 编码
te_ary = te.fit_transform(dataset)
df = pd.DataFrame(te_ary, columns=te.columns_)
# 利用 Apriori 找出频繁项集
freq = apriori(df, min_support=0.05, use_colnames=True)
print(freq)运行结果如下:
购物篮分析
购物篮分析(Market Basket Analysis)是一种在零售业非常流行的技术,用于发现顾客购买产品之间的关联规则。
输入和输出
- 输入: 一组交易数据,每一笔交易包含多个购买的商品。
- 输出: 满足最小支持度和最小置信度的关联规则。
Python实现代码
首先导入必要的库:
from itertools import chain, combinations
接着定义几个辅助函数:
# 生成候选项集的所有非空子集
def powerset(s):
return chain.from_iterable(combinations(s, r) for r in range(1, len(s)))
# 计算支持度
def calculate_support(itemset, transactions):
return sum(1 for transaction in transactions if itemset.issubset(transaction)) / len(transactions)
现在我们来实现Apriori算法:
def apriori(transactions, min_support, min_confidence):
# 初始化频繁项集和关联规则列表
frequent_itemsets = []
association_rules = []
# 第一步:找出单项频繁项集
singletons = {frozenset([item]) for transaction in transactions for item in transaction}
singletons = {itemset for itemset in singletons if calculate_support(itemset, transactions) >= min_support}
frequent_itemsets.extend(singletons)
# 迭代找出所有其他频繁项集
prev_frequent_itemsets = singletons
while prev_frequent_itemsets:
# 生成新的候选项集
candidates = {itemset1 | itemset2 for itemset1 in prev_frequent_itemsets for itemset2 in prev_frequent_itemsets if len(itemset1 | itemset2) == len(itemset1) + 1}
# 计算支持度并筛选
new_frequent_itemsets = {itemset for itemset in candidates if calculate_support(itemset, transactions) >= min_support}
frequent_itemsets.extend(new_frequent_itemsets)
# 生成关联规则
for itemset in new_frequent_itemsets:
for subset in powerset(itemset):
subset = frozenset(subset)
diff = itemset - subset
if diff:
confidence = calculate_support(itemset, transactions) / calculate_support(subset, transactions)
if confidence >= min_confidence:
association_rules.append((subset, diff, confidence))
prev_frequent_itemsets = new_frequent_itemsets
return frequent_itemsets, association_rules
示例和输出
假设我们有以下简单的购物数据集:
transactions = [
{'牛奶', '面包', '黄油'},
{'啤酒', '面包'},
{'牛奶', '啤酒', '黄油'},
{'牛奶', '鸡蛋'},
{'面包', '鸡蛋', '黄油'}
]
调用Apriori算法:
min_support = 0.4
min_confidence = 0.5
frequent_itemsets, association_rules = apriori(transactions, min_support, min_confidence)
print("频繁项集:", frequent_itemsets)
print("关联规则:", association_rules)
输出可能如下:
频繁项集: [{'牛奶'}, {'面包'}, {'黄油'}, {'啤酒'}, {'鸡蛋'}, {'牛奶', '面包'}, {'牛奶', '黄油'}, {'面包', '黄油'}, {'啤酒', '黄油'}, {'面包', '啤酒'}]
关联规则: [(('牛奶',), ('面包',), 0.6666666666666666), (('面包',), ('牛奶',), 0.6666666666666666), ...]
通过这个实战应用,我们不仅学习了如何在Python中实现Apriori算法,还了解了它在购物篮分析中的具体应用。这为进一步的研究和实际应用提供了有用的指导。
完整代码:
# 1.导入必要的库
from itertools import chain, combinations
# 2.定义机构赋值函数
# 生成候选项集的所有非空子集
def powerset(s):
return chain.from_iterable(combinations(s, r) for r in range(1, len(s)))
# 计算支持度
def calculate_support(itemset, transactions):
return sum(1 for transaction in transactions if itemset.issubset(transaction)) / len(transactions)
# 3.实现Apriori算法
def apriori(transactions, min_support, min_confidence):
# 初始化频繁项集和关联规则列表
frequent_itemsets = []
association_rules = []
# 第一步:找出单项频繁项集
singletons = {frozenset([item]) for transaction in transactions for item in transaction}
singletons = {itemset for itemset in singletons if calculate_support(itemset, transactions) >= min_support}
frequent_itemsets.extend(singletons)
# 迭代找出所有其他频繁项集
prev_frequent_itemsets = singletons
while prev_frequent_itemsets:
# 生成新的候选项集
candidates = {itemset1 | itemset2 for itemset1 in prev_frequent_itemsets for itemset2 in prev_frequent_itemsets if len(itemset1 | itemset2) == len(itemset1) + 1}
# 计算支持度并筛选
new_frequent_itemsets = {itemset for itemset in candidates if calculate_support(itemset, transactions) >= min_support}
frequent_itemsets.extend(new_frequent_itemsets)
# 生成关联规则
for itemset in new_frequent_itemsets:
for subset in powerset(itemset):
subset = frozenset(subset)
diff = itemset - subset
if diff:
confidence = calculate_support(itemset, transactions) / calculate_support(subset, transactions)
if confidence >= min_confidence:
association_rules.append((subset, diff, confidence))
prev_frequent_itemsets = new_frequent_itemsets
return frequent_itemsets, association_rules
# 4.示例和输出
transactions = [
{'牛奶', '面包', '黄油'},
{'啤酒', '面包'},
{'牛奶', '啤酒', '黄油'},
{'牛奶', '鸡蛋'},
{'面包', '鸡蛋', '黄油'}
]
# 5.调用Apriori算法
min_support = 0.4
min_confidence = 0.5
frequent_itemsets, association_rules = apriori(transactions, min_support, min_confidence)
print("频繁项集:", frequent_itemsets)
print("关联规则:", association_rules)运行结果如下:
频繁项集: [frozenset({'牛奶'}), frozenset({'面包'}), frozenset({'鸡蛋'}), frozenset({'啤酒'}), frozenset({'黄油'}), frozenset({'黄油', '牛奶'}), frozenset({'黄油', '面包'})]
关联规则: [(frozenset({'黄油'}), frozenset({'牛奶'}), 0.6666666666666667), (frozenset({'牛奶'}), frozenset({'黄油'}), 0.6666666666666667), (frozenset({'黄油'}), frozenset({'面包'}), 0.6666666666666667), (frozenset({'面包'}), frozenset({'黄油'}), 0.6666666666666667)]
![]()