【LeetCode-简单】136. 只出现一次的数字 - 位运算

136. 只出现一次的数字

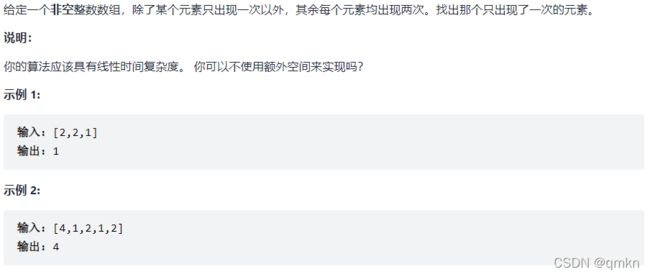
如果不考虑时间复杂度和空间复杂度的限制，这道题有很多种解法，可能的解法有如下几种：

• 使用集合存储数字。遍历数组中的每个数字，如果集合中没有该数字，则将该数字加入集合，如果集合中已经有该数字，则将该数字从集合中删除，最后剩下的数字就是只出现一次的数字。
• 使用哈希表存储每个数字和该数字出现的次数。遍历数组即可得到每个数字出现的次数，并更新哈希表，最后遍历哈希表，得到只出现一次的数字。
• 使用集合存储数组中出现的所有数字，并计算数组中的元素之和。由于集合保证元素无重复，因此计算集合中的所有元素之和的两倍，即为每个元素出现两次的情况下的元素之和。由于数组中只有一个元素出现一次，其余元素都出现两次，因此用集合中的元素之和的两倍减去数组中的元素之和，剩下的数就是数组中只出现一次的数字。

上述三种解法都需要额外使用 O(n) 的空间，其中 n 是数组长度。

解法一：排序+遍历

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        if(nums.size()==1) return nums[0];
        sort(nums.begin(),nums.end());
        int i;
        for(i=0;i<nums.size();i++){
            if(nums[i]==nums[i+1]){
                i++;
            }else{
                break;
            }
        }
        return nums[i];
    }
};

解法二：位运算
使用位运算能做到线性时间复杂度和常数空间复杂度。对于这道题，可使用异或运算 ⊕。异或运算有以下三个性质。

1. 任何数和 0 做异或运算，结果仍然是原来的数，即 a⊕0=a。
2. 任何数和其自身做异或运算，结果是 0，即 a⊕a=0。
3. 异或运算满足交换律和结合律，即 a⊕b⊕a=b⊕a⊕a=b⊕(a⊕a)=b⊕0=b。

假设数组中有 2m+1 个数，其中有 m 个数各出现两次，1个数出现一次。令 a1, a2 ,…, am 为出现两次的 m 个数，a(m+1) 为出现一次的数。根据性质 3，数组中的全部元素的异或运算结果总是可以写成如下形式：

(a1 ⊕a1)⊕(a2 ⊕a2)⊕⋯⊕(am ⊕am )⊕a(m+1)

​根据性质 2 和性质 1，上式可化简和计算得到如下结果：

0⊕0⊕⋯⊕0⊕a(m+1) =a(m+1)

因此，数组中的全部元素的异或运算结果即为数组中只出现一次的数字。

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int ans=0;
        for(int i=0;i<nums.size();i++){
            ans ^=nums[i];
        }
        return ans;
    }
};