数据结构中关于树的知识(java代码实现)
整体上,大概一万字,有点长,是我学习树的笔记。代码都是可以运行的,算法基本是没问题的,是我自己实现的。测试用例通过了。
树
定义
n(n>=0)个节点的有限集合。如果n=0表示空树。在非空树中,有且只有一个特殊节点称为根节点。当
n>1时,其余节点可分为m个互不相交的有限集合。每个有限集合,又遵循此定义。
树的定义是递归的,由根节点的其他若干个互不相交的子树组成。每个子树,又是如此的定义,所以是递归的。因此,关于树的算法也常用递归算法。
树的表现形式
集合形式 、 凹入表示、广义表、 图形结构
树的术语
- 节点的度 :节点的子树个数
- 树的度:所有节点中最大的度数
- 路径和路径长度:一个节点到另外一个节点的节点序列叫路径。路径长度:节点序列的个数-1
- 树的深度/高度:节点的最大层次。
- 有序树:树中节点的各子树从左到右有次序,最左边的第一个孩子。(此时,子树的位置不可交换,并且顺序是相对的,相对其他子树)
- 森林:m(>=0) 棵互不相交的树的集合。树一定是森林,但是森林不一定是树(可能是多颗树)
二叉树
对于普通树而言,运算是复杂的,叉的个数是不确定的。二叉树的结构简单,有规律,最多两个叉,运算是简单的。
并且普通的树是可以抓换为唯一对应的二叉树的,二叉树也可以转回去。因此,我们研究二叉树。
定义
n(>=0)个节点的有限集。当n=0时时空集。n>1时由一个根节点和两颗互不相交的左右子树(也是二叉树)组成。
- 每个节点最多有两个孩子
- 子树有左右之分,不能颠倒
- 可以有空的左右子树
二叉树不是树的特殊情况
二叉树和树不是一个概念。
二叉树的子树是要区分左右子树的,即使只有一个子树,也是要区分左右的,这点有别于有序树。树中只有一个孩子时候,是不需要区分左右的。这点是二叉树和树 ,最大的区别。
二叉树是有序的,但是不是有序树,有序树是树下面的概念。
二叉树和树都是树形结构,树形结构不是树独有的。
二叉树的五种基本形态
- 空树
- 只有根
- 根和左子树
- 根和有子树
- 根和左、右子树
二叉树抽象数据类型定义
ADT BinaryTree{
数据对象D:
数据关系R:
基本操作P:
// definition 是根据哪一种遍历关系,构造二叉树
CreateBiTree(T,definition);
PreOrderTraverse(T);
PreOrderTraverse(T);
PreOrderTraverse(T);
}
二叉树性质
- 第 i(>=1) 层上,最多有2i-1 个节点。(1 2 4 8 ... 等比数列)
- 深度为 K 的二叉树,总共之多有 2k - 1 个节点(K>=1)。等比数列求和公式
- n2 = n0 + 1
性质三的说明:
从下往上看:
每个节点都有一条边和双亲节点相连,除了根节点,因此总边数(B)节点总数(n)-1。
从上往下看:
度为2的节点有2条边,度为1的节点有1条边,度为0的节点没有边。
因此 B = n -1 = n2*2+n1。而 n = n0+n1+n2 。
所以 n0 = n2 + 1 。
这种思想,可推广到任何一棵树,树的节点总数 = 边的数量 + 1 。
两种特殊形式的二叉树
这两种特殊形式的二叉树,在顺序存储下是可以复原的。
满二叉树
- 每一层的节点都是最大节点数,每一层都是满的。
- 叶子结点全部在最底层。
- 在同样深度的二叉树中,节点个数最多,叶子节点也是最多。
完全二叉树
与满二叉树为蓝本,只能从叶子节点,从右往左顺序的连续减少节点。满二叉树是完全二叉树。
完全二叉树中的节点与满二叉树中的节点一一对应。
- 叶子节点,只能出现在最大的两层上。
- 对于任意一个节点,如果其右子树的最大层次为 i ,则其左子树的最大层次必为 i 或 i+1
性质
1、具有 n 个节点的完全二叉树的深度为 ⌊ l o g 2 n ⌋ \lfloor log2n \rfloor ⌊log2n⌋ + 1 。
假设一共 K 层,K-1 层及其之上的节点加起来,一共有 2k-1-1 个节点。
同理,K 层及其之上的节点加起来,最多有 2k-1 个节点
所以, 2k-1-1 < n < 2k-1 个节点
解出 K 。
2、双亲节点和孩子节点之间的关系
- 如果 i=1 ,则节点是二叉树的根,无双亲;如果 i>1 ,则其双亲是节点 i/2.
- 如果 2i > n ,则节点 i 没有左孩子,否则,其左孩子是节点 2i 。
- 如果 2i+1 > n ,则节点 i 没有右孩子,否则,其右孩子是节点 2i+1 。
二叉树的存储结构
顺序存储结构
按照满二叉树的节点层次编号,用数组依次存放二叉树中的数据元素。缺的节点用特殊元素代替。
数组中从下标 1 开始存,比较方便使用性质。节点关系隐藏在数组下标之中。
缺点
- 新节点的添加,需要移动大量元素。
- 浪费空间。最坏情况:右单支树,浪费大量空间。
因此只适合满二叉树、完全二叉树的存储。
链式存储
1、二叉链表
主要是为了找后继,节点中定义有元素域,左右孩子域。
在 n 个节点的二叉链表中,有2n-(n-1) = n+1 个空指针域。
一共 n 个节点,一共有 2n 个指针域,然后除了根节点,没有双亲,其他 n-1 个节点,都有自己的双亲,需要占用 n-1 个指针域,所以剩下 n+1 个空指针域。
2、三叉链表
不但需要找后继,还需要找前驱。在二叉链表的基本上,再加一个指向双亲的指针域。
遍历二叉树
访问节点,打印输出,或者修改节点值。但是不能破坏原有的数据结构,即不插入、删除节点。
每个节点仅访问一次,也称周游。遍历是重中之重,是后面二叉树其他算法的基础。
访问的时候,规定了,左右孩子的访问顺序,必须是先左后右,因此,根节点的访问,只能插入到左右之间,一共有三种遍历方法:DLR,LDR,LRD 。
递归算法
树的定义是递归的,因为访问也是递归算法。因为树,一共分为三部分,根节点、左子树、右子树。
遍历的,只需要处理这三部分即可,因为左右子树,又是一颗树,又分为这三部分,循环往复,递归处理。
遍历的时候,牢记先左后右。
从递归的角度看,三种算法是一样的,访问路径是相同的,只是访问节点的时机不一样。
代码没啥写的,太简单了。
时间复杂度:O(n)
每个节点一共经过三次,
3n次。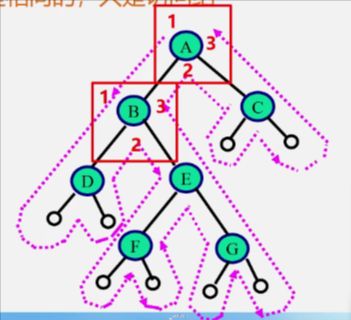
第一次经过时访问:先序遍历。
第二次经过时访问:中序遍历。
第三次经过时访问:后序遍历。
空间复杂度:O(n)
最快的情况下,单支情况,中途没有回退,n 个节点全部都在栈中,所以,最坏是 o(n) 。
非递归算法
实在不行,就背模板哦。。
基本思想
遍历的过程中需要找左右孩子,而递归算法,都在栈中,访问左子树结束以后,回退,就会回退到双亲节点的栈中,可以直接拿到右孩子。
使用非递归算法,访问左子树的时候,需要把双亲节点保存起来,便于找到右子树,因此需要自己模拟栈保存起来。
也有不需要栈的版本,KMP算法中的M大神发明的。
判断条件,当前节点不为空,或者栈不为空。
当前节点不为空:
当前节点要是为空,直接返回,不为空,才需要进栈,为寻找右子树提供方便。
栈不为空:
栈为空,表示遍历结束。因为经过的节点,无论访问与否,都会加入到栈中,栈空,表示结束。
栈中的元素,表示需要处理的节点,或者已经处理过的节点,只是需要利用它寻找右子树
具体何时处理,看前序还是中序还是后序,也就是一个节点路过三次,看哪一次处理。
只关注根节点的输出。左右子树的输出,不用关心,因为最后左右子树都会转为根节点处理。
三点模型:(逻辑只在这三个点上进行。)
根
/ \
左子树 右子树
中序非递归算法
- 建立一个栈
- 根节点进栈,待会处理,遍历左子树
- 左子树处理完毕,处理根节点,根节点出栈,输出根节点,同时也是利用根节点寻找右子树。
public List<Integer> inOrderTraversal(TreeNode root){
List<Integer> result = new ArrayList<Integer>();
Stack<TreeNode> stack = new Stack<TreeNode>();
TreeNode p = root;
while(p!=null || !stack.empty()){
// 如果当前节点不为空,则继续寻找它的左节点
if(p!=null){
stack.add(p);
p = p.left ;
}else {
// 当前节点为空,就是双亲节点的左节点为空
// 处理双亲节点,处理过的节点从栈中弹出
p = stack.pop() ;
result.add(p.val);
// 转去处理双亲节点的右节点。
p = p.right ;
}
}
return result ;
}
前序非递归算法
- 建立一个栈
- 先处理根节点,进栈根节点,然后处理左子树
- 左子树处理完毕,根节点出栈,利用根节点寻找右子树,遍历右子树。
还有一种写法,将根节点压入栈,然后循环判断栈是否为null,不空则取出栈顶,再先压入右子树,后压入左子树,便于先处理左子树。
感觉并不优雅。反直觉,和遍历的顺序,压根相反。为了先出了,先遍历的后压入。
public List<Integer> PreOrderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<Integer>();
Stack<TreeNode> stack = new Stack<TreeNode>();
TreeNode p = root;
while (p != null || !stack.empty()) {
if (p != null) {
result.add(p.val);
stack.add(p);
p = p.left;
} else {
// 当前节点为空,弹出双亲节点,找右子树。
// 并且前序的栈中元素,在第一遍 遍历的时候,就被处理了,
// 保存在栈里面,只是会了寻找右子树。
// ******************** 重要 **************************
// 做题时候发现的,栈模拟递归还是有点不一样的、
// 正常递归的话,现在的栈顶是不应该弹出的,因为它的右子树还没有出来。
// 应该等右子树处理结束了,再弹栈。
// 不然,顺序是有点问题的,在处理某些问题的时候
// ****************************************************
p = stack.pop();
p = p.right;
}
}
return result;
}
后序非递归算法
- 建立一个栈
- 先遍历左子树
- 左子树处理完毕,再遍历右子树。最后处理根节点
有点不一样,需要记录上一个访问的节点,用来判断是从左子树还是右子树,回到的根节点。其中只记录真实的节点,null 不记录。
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<Integer>();
Stack<TreeNode> stack = new Stack<TreeNode>();
TreeNode p = root, prc = null,temp = null;
while (p != null || !stack.empty()) {
if (p != null) {
stack.push(p);
prc = p ;
p = p.left;
} else {
// 此时 p == null
// 处理根节点
temp = stack.peek();
// 如果根节点的右子树为 null 或者右子树已经处理过了
// 会连续弹栈。
if (temp.right == prc || temp.right == null) {
// prc 是上一次处理的节点.
// 此时处理根节点,根节点就变为上一次处理的节点
prc = stack.pop();
result.add(temp.val);
} else {
// 处理左子树为 null 的情况,跳到右子树
prc = p ;
p = temp.right;
}
}
}
return result;
}
层次遍历
从根节点开始,从上往下,从左往右遍历。
基本思想
- 将根节点入队列
- 队列不空时循环,取出队头元素
-
- 如果有左孩子,将左孩子入队。
- 如果有右孩子,将右孩子入队。
主要是循环队列的使用,自己实现一个循环队列
CircularQueue。容量默认是
10个。其实有个问题一共有
n个元素的二叉树,需要多大容量的循环队列。
public List<Integer> levelOrder(TreeNode root) {
ArrayList result = new ArrayList<Integer>();
CircularQueue circularQueue = new CircularQueue<TreeNode>(TreeNode.class,10);
if (root == null) {
return result;
}
circularQueue.add(root);
while (!circularQueue.empty()) {
TreeNode node = (TreeNode) circularQueue.take();
result.add(node.val);
if (node.left != null) {
if (!circularQueue.add(node.left)) {
System.out.println("队列满");
}
}
if (node.right != null) {
if (!circularQueue.add(node.right)) {
System.out.println("队列满");
}
}
}
return result;
}
遍历算法的应用
建立二叉树
根据前序创建二叉树,比较符合逻辑。容易理解
中序,无法创建。
后序,层次也可以创建。
这里的前中后序,层次,都是补全的。并且,补全只需要补充出节点的空节点即可,不需要补全成完全二叉树。
不补全的,通过一个单独的序列是无法创建二叉树的。
前序创建二叉树
思想也特别简单。就像将大象关进冰箱一样,建立二叉树也是一样的三部曲:先建立根节点,然后建立左右子树。
和递归遍历思想一样,都是最后转到根节点处理。每个节点最后都是当做根节点处理。
// java没有引用传递,因此需要静态变量,在整个递归中,控制index。
private static int index = 0;
public TreeNode createBiTreeByPreOrder(String strBiTree) {
// 判断字符串是否结束
if (index >= strBiTree.length()) {
return null;
}
char c = strBiTree.charAt(index++);
if (c == '#') {
return null;
} else {
TreeNode node = new TreeNode();
// char 字符数字 转为 int 数字,不然 `1` = 49 。
node.val = c - '0';
// 这里面 i 有个技巧,不能简单的 i++ ;
// 因为 i 需要在整个递归中 增长。
// 如果是完全二叉树,则可以使用性质:双亲节点为 i ,则左孩子 2i,右孩子是 2i+1.
// 因为这里不是完全二叉树,所以使用 全局变量 index
// 先创建左子树,再创建右子树,顺序不能颠倒
node.left = createBiTreeByPreOrder(strBiTree);
node.right = createBiTreeByPreOrder(strBiTree);
return node;
}
}
后序创建二叉树
通过二叉树和后序序列的观察,是可以找到规律的。
最后一个节点是根节点,所以反向遍历
倒数第二个节点是根节点的右孩子,倒数第三个节点是根节点的右孩子的右孩子,然后倒数第四个节点是根节点的右孩子的左孩子。
所以代码中 先处理右子树,再处理左子树
并且后序序列,从左到右也是,左子树 --> 右子树 --> 根节点。
因此反过来建设二叉树。
// java没有引用传递,因此需要静态变量,全局控制index。
private static int index = 等于序列长度-1;
public TreeNode createBiTreeByPostOrder(String strBiTree) {
// 判断字符串是否结束
if (index < 0) {
return null;
}
// 反向遍历 全局变量 index 减--
char c = strBiTree.charAt(index--);
if (c == '#') {
return null;
} else {
TreeNode node = new TreeNode();
node.val = c - '0';
// 先创建右子树
node.right = createBiTreeByPostOrder(strBiTree);
node.left = createBiTreeByPostOrder(strBiTree);
return node;
}
}
层次遍历创建二叉树
比较方便,不像前序,后序,需要自己写出序列,层次的序列好写。
思路:
先创建根节点,然后依次读取序列,创建根节点的左右子树,并且添加到队列中,然后取队头为新的根节点,循环往复,直到队列为空。
其中读取序列,每次读取两个,分别为左右子树的值。
public TreeNode createBiTreeByLevelOrder(String strBiTree) {
CircularQueue<TreeNode> queue = new CircularQueue<TreeNode>(TreeNode.class, 10);
// 判断字符串是否结束
if (0 == strBiTree.length()) {
return null;
}
int i = 0 ;
char c = strBiTree.charAt(i++);
if (c == '#') {
return null;
} else {
// 创建根节点
TreeNode node = new TreeNode();
node.val = c - '0';
// 创建根节点入队
queue.add(node);
while (!queue.empty()) {
TreeNode take = queue.take();
// 左子树
c = strBiTree.charAt(i++);
if (c == '#') {
take.left = null;
} else {
TreeNode temp = new TreeNode();
temp.val = c - '0';
take.left = temp;
queue.add(temp);
}
// 右子树
c = strBiTree.charAt(i++);
if (c == '#') {
take.right = null;
} else {
TreeNode temp = new TreeNode();
temp.val = c - '0';
take.right = temp;
queue.add(temp);
}
}
return node;
}
}
复制二叉树
利用前序遍历思想,先复制根节点,再复制左右子树。
好像也可以选择任何一种遍历方法复制二叉树。
public TreeNode copyBiTree(TreeNode root) {
if (root == null) {
return null;
}
// 处理根节点
TreeNode node = new TreeNode();
node.val = root.val;
// 处理左右子树
node.left = copyBiTree(root.left);
node.right = copyBiTree(root.right);
return node;
}
计算二叉树的深度
分别求出左右子树的深度,大的值加一(加上根),就是树的深度。
思想,还是用三点模型,当前节点的深度,就是其左右子树的较大深度+1。
depth就是求节点的深度,所以直接递归调用。
public int depth(TreeNode root) {
if (root == null) {
return 0;
}
// 递归求,左右子树的深度
int left = depth(root.left);
int right = depth(root.right);
// 当前根节点的深度,就是左右子树深度的较大值+1
return left > right ? left + 1 : right + 1;
}
计算二叉树节点个数
计算出左右子树的节点个数,再加上根节点。
还是递归的思想:当前根节点的节点个数 = 左右子树的个数 + 1 。而
countNode就是计算当前根节点的节点个数,所以递归的调用它。主要在于函数上,本身就是做这件事的。
public int countNode(TreeNode root) {
if (root == null) {
return 0;
}
int left = countNode(root.left);
int right = countNode(root.right);
return left + right + 1;
}
计算二叉树叶子节点个数
public int countLeafNode(TreeNode root) {
if (root == null) {
return 0;
// 如果是叶子节点,则返回 1 。
} else if (root.left == null && root.right == null) {
return 1;
} else {
// 递归思想:
// 叶子节点 = 左子树的叶子 + 右子树的叶子
return countLeafNode(root.left) + countLeafNode(root.right);
}
}
遍历确定二叉树
中序确定左右子树,先,后序确定根。因此,必须有中序,再加一个前序或者后序。
递归的解决,先处理当前根节点,再处理当前 根节点的左右子树。
思路
- 根据前序或者后序,先找到当前根节点
- 然后在中序中,划分数组。根据当前根节点划分为左右两部分。左边的为左子树,右边的为右子树
- 然后当前根节点的左子树,就是中序数组的左边。当前根节点的右子树就是中序数组的右边。
- 前序或者后序数组的划分,并没有当前根节点这种标志,如果要根据元素划分,需要遍历中序数组,一个一个确认。
- 更快的方法是,中序和前序、后序数组的长度总是一样的,因为是同一棵树的遍历序列。所以中序数组划分以后,中序的左数组的长度就是前序、后序数组划分以后左数组的长度。
- 核心就在划分数组上。
代码
public class Solution {
public TreeNode reConstructBinaryTree(int [] pre,int [] vin) {
// 数组为空,则直接返回
if(pre.length == 0){
return null ;
}
// 否则根据前序,获取第一个元素,就是当前的根节点
TreeNode root = new TreeNode(pre[0]);
// 长度为 1,说明已经是叶子节点了
if(pre.length == 1){
return root ;
}
// 如果不是叶子节点,则进行数组切割
// 以根节点为界线
int division = root.val ;
int index = -1 ;
for(int i = 0;i<vin.length;i++){
if(division == vin[i]){
// 找到边界的下标
index = i ;
break ;
}
}
// 中序数组,以根节点为分界线,分割
int[] vinleft = new int[index] ;
int[] vinright = new int[vin.length - index-1] ;
for(int i = 0 ; i<index;i++){
vinleft[i] = vin[i];
}
for(int i = index+1 ; i<vin.length;i++){
vinright[i-index-1] = vin[i];
}
// 前序数组的分割,更简单,想明白以后
// 中序,根据特定的节点,前序数组没有这个特点
// 但是左右子树的元素数量,在前中序中是一样的。
// 所以前序直接根据中序的数组长度分
int[] preleft = new int[index] ;
int[] preright = new int[vin.length - index-1] ;
for(int i = 1 ; i<=index;i++){
preleft[i-1] = pre[i] ;
}
for(int i = index+1 ; i<vin.length;i++){
preright[i-index-1] = pre[i];
}
// 递归的处理左右子树
root.left = reConstructBinaryTree(preleft,vinleft);
root.right = reConstructBinaryTree(preright,vinright);
return root ;
}
}
线索二叉树
链表存储二叉树,很方便寻找孩子节点。
但是一般情况下,无法直接找到一个节点,在某种遍历序列中的前驱和后继。
如果需要寻找给定节点的前驱或者后继,是需要再一次递归遍历二叉树的。
线索化以后,可以直接通过
next方法找到,虽然next也是遍历,但是不是全部遍历,比从头遍历快得多。
意义
线索化以后,不需要再遍历了,可以通过线索,很快的找到前驱后继。也就是
next方法这里的前驱后继,不是二叉树中的前驱后继,是遍历序列中的前驱后继。
只有中序遍历实现的线索二叉树,可以很好的解决寻找前驱后继。
必备姿势
中序线索二叉树,需要对中序遍历,有良好的认知,里面代码的编写,有的地方,直接涉及到遍历思路:
1、 当前根节点的后继节点,应该在其右子树的最左边 当前根节点的后继节点,应该在其右子树的最左边
2、 中序遍历的第一个节点是:左子树的最左边节点。
如果你不能理解上面的
2句话,那想理解线索二叉树够悬。
线索
利用链表二叉树中的空指针域,如果左孩子为空,则让其指向前驱节点;如果右孩子为空,则让其指向后继节点。
加上线索的二叉树,称为 线索二叉树。
线索化
对二叉树按照某种遍历次数使其变为线索二叉树的过程。
// 线索二叉树节点的定义
public class ThreadTreeNode {
int val;
ThreadTreeNode left;
ThreadTreeNode right;
byte lTag, rTag;
}
注:不增加指针域,而是增加标记位 lTag rTag。是为了节省空间。标记为用byte 只需要一个字节,引用则需要4或者8 个字节。
中序遍历线索化
线索化,不同的实现有细节差别,这种差别体现在具体的算法上。
比如,我这里实现的版本,是没有额外的头结点的,所以整个线索化以后。中序序列的第一个元素的左孩子,最后一个元素的右孩子都是
null.
private static ThreadTreeNode pre = null;
public ThreadTreeNode inThreadTree(ThreadTreeNode root) {
if (root == null) {
return null;
}
// 左子树线索化
inThreadTree(root.left);
if (root.left == null) {
root.lTag = 1;
root.left = pre;
}
if (pre != null && pre.right == null) {
pre.rTag = 1;
pre.right = root;
}
// 维护 pre 。始终指向前一个访问的节点
pre = root;
// 右子树线索化
inThreadTree(root.right);
return root;
}
next 方法实现
这是找中序序列后继的方法。再提醒一下,不是找二叉树的后继,这不用找。
核心思思是: 当前根节点的后继节点,应该在其右子树的最左边
根据中序遍历,其实是容易理解的。
public TreeNode next(TreeNode node) {
if (node.rTag == 1) {
return node.right;
}
// 否则,根据中序遍历的思路。
// 当前根节点的后继节点,应该在其右子树的最左边
node = node.right;
// 序列的最后一个节点
if (node == null) {
return null;
}
// lTag 为 0 表示是左子树,不能判断 left != null。
// 线索化以后,right ,left 有值,不一定是左子树,可能是前驱,所以只能根据标记判断。
while (node.lTag == 0) {
node = node.left;
}
return node;
}
prior 方法实现
找前驱的方法。
和
next方法一样的思路。
public TreeNode prior(TreeNode node) {
if (node.lTag == 1) {
return node.left;
}
// 否则,根据中序遍历的思路。
// 当前根节点的前驱节点,应该在其左子树的最右边
node = node.left;
// 序列的第一个节点
if (node == null) {
return null;
}
// rTag 为 0 表示是左子树,不能判断 right != null。
// 线索化以后,right ,left 有值,不一定是左子树,可能是前驱,所以只能根据标记判断。
while (node.rTag == 0) {
node = node.right;
}
return node;
}
中序遍历线索二叉树
一切尽在注释中
public List<Integer> inOrderTraversalThreadBiTree(ThreadTreeNode root) {
ArrayList<Integer> result = new ArrayList<>();
// 查找中序遍历的第一个节点:
// 中序遍历思路,左子树的最左边的节点,就是第一个节点。
// 也就是第一个左孩子为 null ,lTAG == 1 的节点
if (root == null) {
return null;
}
while (root.lTag == 0) {
root = root.left;
}
// 此时 root 就是中序遍历的第一个节点
result.add(root.val);
// 下面使用线索二叉树的遍历方法,不用递归,用 next 方法
// 条件还记得吧,只有最后一个节点的右孩子为 null
while (root.right != null) {
// 使用 我们实现的 next,寻找后继。
root = next(root);
result.add(root.val);
}
return result;
}
总结
线索二叉树的意义,在于,更快地寻找序列的前驱和后继节点。线索化以后,可以通过 next , prior 方法更快地寻找前驱后继,不需要每次都再遍历一次二叉树。开销变小了,相当于将树形结构的遍历,改为链表的遍历。
实现的思路顺序:
需要先有一颗二叉树,然后线索化这棵二叉树。线索化以后才能实现 next , prior 方法。有了 next , prior 方法 ,才能实现类似链表的遍历。
森林
森林 是m(m≥0)棵互不相交的树的集合。任何一棵树,删除了根结点就变成了森林。
0棵树或者1棵树也能称为森林。
树的存储结构
双亲表示法
找双亲容易,找孩子复杂一点。适用于经常寻找双亲的操作。
孩子链表
适用于经常寻找孩子的操作。
n个节点n个单链表。
带双亲的孩子链表
孩子兄弟表示法
最大的优点:将一颗复杂的树,变为二叉树。然后可以利用二叉树的性质,处理它。
也叫二叉树表示法、二叉链表表示法。
两个指针域,一个指向第一个孩子,一个指向下一个兄弟节点。长兄如父。
找孩子:容易,通过给定的节点的孩子域,找到第一个孩子,然后通过第一个孩子的兄弟域,找到所有孩子。
找兄弟:容易查找右边的兄弟,左边的兄弟不容易找到。
找双亲:复杂,如有需要,可以添加指向双亲的指针域。
树和二叉树的转换
直接研究树,比较复杂,树千变万化。而二叉树相对容易,二叉树的相关算法前面已经研究过了。因此如果能将树转换为二叉树进行处理,事情将变得简单。
树和二叉树都可以用二叉链表作为存储结构,也就是二叉链表,既可以解释为树,也可以解释为二叉树。
因此,可以将树用二叉链表表示,然后将此二叉链表解释为二叉树,然后用二叉树的算法处理。
一颗树对应唯一的二叉树。
树变二叉树
利用孩子兄弟表示法 。简记:兄弟相连留长子。
变为二叉树以后,以前树的兄弟节点,都变为右子树。
二叉树变为树
反向操作,之前是兄弟节点都变为右子树。现在将一个节点的所有右孩子,都与该节点的双亲节点相连。
森林和二叉树的转换
森林变为二叉树
将每一棵树都变为二叉树,然后将各个二叉树的根相连。
由于树变二叉树,是没有右子树的,所以后面的二叉树,都连接在前一个二叉树的根节点的右子树上。
二叉树变为森林
将二叉树的根节点的右孩子,递归的断开。就变成许多棵单独的二叉树,这些二叉树,再转换为树,就变回森林。
树与森林的遍历
树的遍历
只有三种遍历方式,没有中序遍历,因为树可以有多个子树,不知道哪里算中间。
树的前序遍历对应于转换后的二叉树的前序遍历。树的后序遍历对应于转换后的二叉树的中序遍历。
森林的遍历
将森林看作三部分:
- 第一棵树的根节点
- 第一棵树的子树森林
- 其他树构成的森林
递归的执行上面的 1,2,3 。
将访问第一棵树的根节点的时机,分为先序,中序。
前序遍历森林
按照顺序 1,2,3 访问森林的三个部分。或者从左到右,依次对每一棵树进行先根遍历。
中序遍历森林
按照顺序 2,1,3 访问森林的三个部分。或者从左到右,依次对每一棵树进行后根遍历。
哈夫曼树
也叫最优二叉树。
树的路径长度
树根到每一个节点(不是叶子节点)的路径长度之和,记住TL。
节点数相等二叉树中,完全二叉树的路径长度最短。但是路径长度最短的树,不要一定是完全二叉树。可以把最后一层的节点,往右放。
权和带权路径长度
权:树中的节点赋予一个有着某种含义的数值,称这个值是该节点的权。
节点的带权路径长度:从根节点到该节点的路径长度*该节点的权值。
树的带权路径长度(WPL):树中所有叶子节点的带权路径长度之和。
哈夫曼树
最优树,带权路径长度最短的树。
这里比较有个前提,树的度要一样,要么全是二叉树、要么三叉树。
哈夫曼树是最优二叉树。具有相同带权节点的哈夫曼树不唯一。
前面提到满二叉树是树的路径长度最短。但是满二叉树不一定是哈夫曼树,因为有了权重。
权值越大的节点距离根节点越近。权值越小距离根节点越远。所以在构造哈夫曼树的时候,使用贪心算法,首先选择权值小的节点当叶子节点。
哈夫曼算法
思想
- 将
N个带权节点,每一个当做根节点,构建具有N棵树的森林。 - 选择两个最小的权值节点,合并为一颗二叉树,根节点权值,为新的权值,放进森林中。
- 在新的森林中,继续第二步操作,直到最后剩下一棵树,即是哈夫曼树。
哈夫曼树节点的度,要么是0要么是2,没有1 。
N个节点要变为哈夫曼树,两两合并为一,那么一共需要合并N-1次,产生N-1个节点,加上原来的N个节点,一共是2N-1个节点。
生成的哈夫曼树,最多N-1层。
代码实现
采用顺序结构存储哈夫曼树。
四个数据域:parent,weigth ,rchild,lchild
class huffmanNode {
int weigth;
int parent, lchild, rchild;
}
哈夫曼算法的实现
细节可能不一样的地方,因为我们从
1开始使用,数组0下标没有使用。所以,
for循环的开始下标是1。并且填充的默认值是
0。
/**
* 创建 哈夫曼树
*
* @param weigths 权值节点数组
* @return 返回保存哈夫曼树的数组
*/
public huffmanNode[] createhuffman(int[] weigths) {
int length = weigths.length;
// 哈夫曼树需要 2N-1 个节点
huffmanNode[] huffmanNodes = new huffmanNode[length * 2];
// 初始化数组,将所有的值都设置为 0 值
for (int i = 0; i < huffmanNodes.length; i++) {
huffmanNodes[i] = new huffmanNode();
huffmanNodes[i].parent = 0;
huffmanNodes[i].lchild = 0;
huffmanNodes[i].rchild = 0;
huffmanNodes[i].weigth = 0;
}
// 设置带权节点
for (int i = 1; i <= length; i++) {
huffmanNodes[i].weigth = weigths[i - 1];
}
// 哈夫曼算法
// 每次选两最小的节点,执行 N-1 次
for (int i = length + 1; i < huffmanNodes.length; i++) {
int[] min = selectMin(huffmanNodes);
// 设置两个最小的节点的 parent 数据
huffmanNodes[min[0]].parent = i;
huffmanNodes[min[1]].parent = i;
// 设置新节点的 权重 和 左右孩子
huffmanNodes[i].weigth = huffmanNodes[min[0]].weigth + huffmanNodes[min[1]].weigth;
huffmanNodes[i].rchild = min[0];
huffmanNodes[i].lchild = min[1];
}
return huffmanNodes;
}
// 这个取 最小的 2个的算法,及其不优雅
// 这里不需要考虑,只有一个符合要求的节点了,找不到2个的情况。
// 因为一共 N 个节点。执行N-1次
// 所以最后一定会有至少2个 huffmanNodes[i].parent == 0 节点
// 一定每次都会有2 个返回结果
public int[] selectMin(huffmanNode[] huffmanNodes) {
int[] result = new int[2];
// 找所有 parent 为 0, 还没有被合并过的节点
int min = -1;
int index = 0;
for (int i = 1; i < huffmanNodes.length; i++) {
int weigth = huffmanNodes[i].weigth;
if (huffmanNodes[i].parent == 0 && weigth != 0) {
if (min == -1) {
min = weigth;
index = i;
} else if (weigth <= min) {
min = weigth;
index = i;
}
}
}
result[0] = index;
min = -1;
for (int i = 1; i < huffmanNodes.length; i++) {
if (i == result[0]) {
continue;
}
int weigth = huffmanNodes[i].weigth;
if (huffmanNodes[i].parent == 0 && weigth != 0) {
if (min == -1) {
min = weigth;
index = i;
} else if (weigth <= min) {
min = weigth;
index = i;
}
}
}
result[1] = index;
return result;
}
哈夫曼编码
等长编码浪费空间。不等长编码,必须要求是前缀码(一组编码中的任一编码都是不其他编码的前缀),否则解码会出现重码。
哈弗曼编码就是前缀码,并且是最优前缀码。
哈夫曼编码保证前缀码的原因:
因为哈夫曼编码,用到哈夫曼树,只有叶子节点才参与编码,中间节点都不会参与编码,所以可以保证是前缀码。
因为哈夫曼编码的最优的原因:
因为哈夫曼树本身就是 带权路径长度最短的树。
只需要将字母出现的频率设为权值,就可让编码最优。
因为我们构造哈夫曼树的时候,从数组下标1开始使用的,并且填充的默认值是 0 ,在哈夫曼编码中会用到这个0。
统计频率
统计频率是哈夫曼编码的第一步,只有知道了字母的出现频率,才能设置权重。
我这里按照出现次数统计:
public Map<Character, Integer> countWeight(String text) {
HashMap<Character, Integer> result = new HashMap<>();
int length = text.length();
for (int i = 0; i < length; i++) {
char c = text.charAt(i);
if (result.containsKey(c)) {
int weight = result.get(c);
result.put(c, ++weight);
} else {
result.put(c, 1);
}
}
return result;
}
哈夫曼编码
还是构造哈夫曼树,然后叶子节点就是需要编码的字符,权值为出现的频率,编码为,左0右1。编码的过程,从叶子节点反向搜索,直到搜到根节点为止。
编码之前,修改下节点属性,添加一个属性域char c,保存节点代表的字符。
class HuffmanNode {
int weigth;
int parent, lchild, rchild;
char c;
}
重写哈夫曼树的算法:
之前是根据权重数组生成,现在根据要加密的文本生成
/**
* 通过文本中字母出现的频率 创建 哈夫曼树
*
* @param text 文本
* @return
*/
public HuffmanNode[] createHuffman(String text) {
Map<Character, Integer> charWeights = countWeight(text);
int length = charWeights.size();
// 哈夫曼树需要 2N-1 个节点
HuffmanNode[] huffmaNodes = new HuffmanNode[length * 2];
// 初始化数组,将所有的值都设置为 0 值
for (int i = 0; i < huffmaNodes.length; i++) {
huffmaNodes[i] = new HuffmanNode();
huffmaNodes[i].parent = 0;
huffmaNodes[i].lchild = 0;
huffmaNodes[i].rchild = 0;
huffmaNodes[i].weigth = 0;
}
// 设置带权节点
Iterator<Map.Entry<Character, Integer>> iterator = charWeights.entrySet().iterator();
int index = 1;
while (iterator.hasNext()) {
Map.Entry<Character, Integer> next = iterator.next();
huffmaNodes[index].weigth = next.getValue();
// 将字符放进叶子节点
huffmaNodes[index].c = next.getKey();
index++;
}
// 每次选两最小的节点,哈夫曼算法
// 执行 N-1 次
for (int i = length + 1; i < huffmaNodes.length; i++) {
int[] min = selectMin(huffmaNodes);
// 设置两个最小的节点的 parent 数据
huffmaNodes[min[0]].parent = i;
huffmaNodes[min[1]].parent = i;
// 设置新节点的 权重 和 左右孩子
huffmaNodes[i].weigth = huffmaNodes[min[0]].weigth + huffmaNodes[min[1]].weigth;
huffmaNodes[i].rchild = min[0];
huffmaNodes[i].lchild = min[1];
}
return huffmaNodes;
}
哈夫曼编码表算法
从叶子节点往上搜索,直到搜索到根节点为止。
public Map<Character, String> huffmanCodeTable(String text) {
HashMap<Character, String> result = new HashMap<>();
Map<Character, Integer> charWeights = countWeight(text);
// 哈夫曼树的数组存储
HuffmanNode[] huffma = createHuffman(text);
// 哈夫曼编码的核心部分,原始的节点,都是叶子节点,所以只计算前N个
Stack<Character> stack = new Stack<>();
for (int i = 1; i <= charWeights.size(); i++) {
int parent = huffma[i].parent;
int temp = i;
// 一直找到 根节点 左0右1
while (parent != 0) {
// 每次判断是左孩子还是右孩子
// 当前节点的下标是 temp ,parent是当前节点的双亲节点
if (huffma[parent].lchild == temp) {
stack.push('0');
} else {
stack.push('1');
}
temp = parent;
parent = huffma[parent].parent;
}
// 取出栈的内容,就是哈夫曼编码
StringBuffer buffer = new StringBuffer();
while (!stack.empty()) {
buffer.append(stack.pop());
}
String code = buffer.toString();
result.put(huffma[i].c, code);
}
return result;
}
编码
public String huffmanCode(Map<Character, String> codeTable, String originalText) {
StringBuffer buffer = new StringBuffer();
for (int i = 0; i < originalText.length(); i++) {
char c = originalText.charAt(i);
buffer.append(codeTable.get(c));
System.out.println(c + " : " + codeTable.get(c));
}
return buffer.toString();
}
解码
解密需要保证和加密用的是相同的哈夫曼树,否则无法解密。
拿着编码的数据,从哈夫曼树的根节点开始寻找,直到走到叶子节点,则对应的编码就是叶子节点代表的字符。然后继续从根节点开始循环。
public String huffmanEncode(HuffmanNode[] huffman, String encryptText) {
StringBuffer buffer = new StringBuffer();
// 最后一个节点是 根节点 ,先拿到根节点
HuffmanNode root = huffman[huffman.length - 1];
// 解码核心代码
for (int i = 0; i < encryptText.length(); ) {
char c = encryptText.charAt(i);
// 从 根节点 遍历哈夫曼树,按照密文的0/1走
if (root.lchild == 0 && root.rchild == 0) {
buffer.append(root.c);
root = huffman[huffman.length - 1];
} else {
if (c == '0') {
root = huffman[root.lchild];
} else {
root = huffman[root.rchild];
}
i++;
}
}
return buffer.toString();
}
注意
这里实现的哈夫曼编码以及解码,只是思想。我们并没有实际的去操作二进制位,而是操控字符串作为代替。
总结
关于树的知识和相关算法,基本都在这。
平衡树和排序树,不在此范围,因为那属于查找部分的知识,后面会更。