贪心算法练习

目录

A - 部分背包问题

B - 均分纸牌 

C -  今年暑假不AC

D -  纪念品分组 

E -  混合牛奶Mixing Milk

F -  迷瘴

G - 国王游戏

H - 跳跳

I -  三国游戏

J - Diong Homework Again

K - Hero

 L - 凌乱的 yyy / 线段覆盖

M - 删数问题

---

A - 部分背包问题

Description

阿里巴巴走进了装满宝藏的藏宝洞。藏宝洞里面有 N(N≤100) 堆金币，第 i 堆金币的总重量和总价值分别是 mi​,vi​(1≤mi​,vi​≤100)。阿里巴巴有一个承重量为 (T≤1000) 的背包，但并不一定有办法将全部的金币都装进去。他想装走尽可能多价值的金币。所有金币都可以随意分割，分割完的金币重量价值比（也就是单位价格）不变。请问阿里巴巴最多可以拿走多少价值的金币？

Input

第一行两个整数 N,T。

接下来 N 行，每行两个整数 mi​,vi​。

Output

一个实数表示答案，输出两位小数

Sample 1

Inputcopy	Outputcopy
4 50 10 60 20 100 30 120 15 45	240.00

Hint 

计算每堆金币的“性价比”（ 总价值 / 总质量 ），排序，因为每堆金币可分割，即利用贪心算法，从性价比高的金币堆开始拿，直到到达最大承重量

#include
using namespace std;
struct jingbi{
	int m,v; //质量，价值
    double zlb;
}jin[120];
bool cmp(jingbi a,jingbi b){
	return a.zlb  >b.zlb  ;//质量比或者可理解为性价比，由高到低排序
}
int n,t;
int main(){
	cin>>n>>t;
	for(int i=0;i>jin[i].m >>jin[i].v;
		jin[i].zlb=jin[i].v*1.0/jin[i].m;//记得*1.0
	}
	
	sort(jin,jin+n,cmp);
	double sum=0;
	for(int i=0;i

B - 均分纸牌 

Description

有 N 堆纸牌，编号分别为 1,2,…,N。每堆上有若干张，但纸牌总数必为 N 的倍数。可以在任一堆上取若干张纸牌，然后移动。

移牌规则为：在编号为 1 堆上取的纸牌，只能移到编号为 2 的堆上；在编号为 N 的堆上取的纸牌，只能移到编号为 N−1 的堆上；其他堆上取的纸牌，可以移到相邻左边或右边的堆上。

现在要求找出一种移动方法，用最少的移动次数使每堆上纸牌数都一样多。

例如 N=4 时，4 堆纸牌数分别为 9,8,17,6。

移动 33 次可达到目的：

• 从第三堆取 4 张牌放到第四堆，此时每堆纸牌数分别为 9,8,13,10。
• 从第三堆取 3 张牌放到第二堆，此时每堆纸牌数分别为 9,11,10,10。
• 从第二堆取 1 张牌放到第一堆，此时每堆纸牌数分别为 10,10,10,10。

Input

第一行共一个整数 N，表示纸牌堆数。
第二行共 N 个整数 A1​,A2​,…,AN​，表示每堆纸牌初始时的纸牌数。

Output

共一行，即所有堆均达到相等时的最少移动次数。

Sample 1

Inputcopy	Outputcopy
4 9 8 17 6	3

Hint

对于 100% 的数据，1≤N≤100，1≤Ai​≤10000。

【题目来源】

NOIP 2002 提高组第一题

 Hint 

假设所有牌都移向右边，移动牌数即现有堆牌数与目标牌数（牌数平均数）差数 ，是负数时其实则可理解为从下一堆移向目前堆。

#include
using namespace std;
int main(){
	int n,a[120];
	int goal=0,ans=0;;
    cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		goal+=a[i];
	}
	goal/=n;//目标牌数即均值
	for(int i=1;i

C -  今年暑假不AC

“今年暑假不AC？”
“是的。”
“那你干什么呢？”
“看世界杯呀，笨蛋！”
“@#$%^&*%...”

确实如此，世界杯来了，球迷的节日也来了，估计很多ACMer也会抛开电脑，奔向电视了。
作为球迷，一定想看尽量多的完整的比赛，当然，作为新时代的好青年，你一定还会看一些其它的节目，比如新闻联播（永远不要忘记关心国家大事）、非常6+7、超级女生，以及王小丫的《开心辞典》等等，假设你已经知道了所有你喜欢看的电视节目的转播时间表，你会合理安排吗？（目标是能看尽量多的完整节目）

Input

输入数据包含多个测试实例，每个测试实例的第一行只有一个整数n(n<=100)，表示你喜欢看的节目的总数，然后是n行数据，每行包括两个数据Ti_s,Ti_e (1<=i<=n)，分别表示第i个节目的开始和结束时间，为了简化问题，每个时间都用一个正整数表示。n=0表示输入结束，不做处理。

Output

对于每个测试实例，输出能完整看到的电视节目的个数，每个测试实例的输出占一行。

Sample

Inputcopy	Outputcopy
12 1 3 3 4 0 7 3 8 15 19 15 20 10 15 8 18 6 12 5 10 4 14 2 9 0	5

#include
#include
#include
using namespace std;
struct TV{
	int strat;
	int end;
}tv[120];
bool cmp(TV a,TV b){
	return a.end =e){
				ans++; e=tv[i].end ;
			}
		}
		printf("%d\n",ans);
	}
	return 0;
}

D -  纪念品分组 

Description

元旦快到了，校学生会让乐乐负责新年晚会的纪念品发放工作。为使得参加晚会的同学所获得 的纪念品价值相对均衡，他要把购来的纪念品根据价格进行分组，但每组最多只能包括两件纪念品， 并且每组纪念品的价格之和不能超过一个给定的整数。为了保证在尽量短的时间内发完所有纪念品，乐乐希望分组的数目最少。

你的任务是写一个程序，找出所有分组方案中分组数最少的一种，输出最少的分组数目。

Input

共 n+2 行：

第一行包括一个整数 w，为每组纪念品价格之和的上限。

第二行为一个整数 n，表示购来的纪念品的总件数 G。

第 3∼n+2 行每行包含一个正整数 Pi​ 表示所对应纪念品的价格。

Output

一个整数，即最少的分组数目。

Sample 1

Inputcopy	Outputcopy
100 9 90 20 20 30 50 60 70 80 90	6

 Hint

数组排序后，双指针搜寻，i 从最大开始，j 从最小开始，a [ i ] + a [ j ] <= goal 则增加组数ans++， i --  ,  j++ ,否则则增加组数ans++, i-- , j 不变.

#include
using namespace std;
const int N=3e4+5;
int a[N];
int n,m;
int main(){
	ios::sync_with_stdio(false);cin.tie(0);
	cin>>n>>m;
	for(int i=1;i<=m;i++)	cin>>a[i]; 
	sort(a+1,a+m+1);
	int num=1,ans=0;
		for(int i=m;i>=num;i--){
			if(a[i]+a[num]<=n){ 
				num++; ans++;
			}
			else ans++;
		}
		cout<

E -  混合牛奶Mixing Milk

Description

由于乳制品产业利润很低，所以降低原材料（牛奶）价格就变得十分重要。帮助 Marry 乳业找到最优的牛奶采购方案。

Marry 乳业从一些奶农手中采购牛奶，并且每一位奶农为乳制品加工企业提供的价格可能相同。此外，就像每头奶牛每天只能挤出固定数量的奶，每位奶农每天能提供的牛奶数量是一定的。每天 Marry 乳业可以从奶农手中采购到小于或者等于奶农最大产量的整数数量的牛奶。

给出 Marry 乳业每天对牛奶的需求量，还有每位奶农提供的牛奶单价和产量。计算采购足够数量的牛奶所需的最小花费。

注：每天所有奶农的总产量大于 Marry 乳业的需求量。

Input

第一行二个整数 n,m，表示需要牛奶的总量，和提供牛奶的农民个数。

接下来 m 行，每行两个整数 pi​,ai​，表示第 i 个农民牛奶的单价，和农民 i 一天最多能卖出的牛奶量。

Output

单独的一行包含单独的一个整数，表示 Marry 的牛奶制造公司拿到所需的牛奶所要的最小费用。

Sample 1

Inputcopy	Outputcopy
100 5 5 20 9 40 3 10 8 80 6 30	630

 Hint

与 A  一样，计算性价比

#include
using namespace std;
struct milkk{
	int m,v;
}milk[5005];
bool cmp(milkk a,milkk b){
	return a.v   >m>>n;//需要牛奶的总量，提供牛奶的农民个数
	for(int i=0;i>milk[i].v >>milk[i].m;//单价，量 
	}
	sort(milk,milk+n,cmp);//单价由低到高 
	int  sum=0;
	for(int i=0;i

F -  迷瘴

通过悬崖的yifenfei，又面临着幽谷的考验――
幽谷周围瘴气弥漫，静的可怕，隐约可见地上堆满了骷髅。由于此处长年不见天日，导致空气中布满了毒素，一旦吸入体内，便会全身溃烂而死。
幸好yifenfei早有防备，提前备好了解药材料（各种浓度的万能药水）。现在只需按照配置成不同比例的浓度。
现已知yifenfei随身携带有n种浓度的万能药水，体积V都相同，浓度则分别为Pi%。并且知道，针对当时幽谷的瘴气情况，只需选择部分或者全部的万能药水，然后配置出浓度不大于 W%的药水即可解毒。
现在的问题是：如何配置此药，能得到最大体积的当前可用的解药呢？
特别说明：由于幽谷内设备的限制,只允许把一种已有的药全部混入另一种之中（即：不能出现对一种药只取它的一部分这样的操作）。

Input

输入数据的第一行是一个整数C，表示测试数据的组数；
每组测试数据包含2行，首先一行给出三个正整数n,V,W(1<=n,V,W<=100)；
接着一行是n个整数，表示n种药水的浓度Pi%(1<=Pi<=100)。

Output

对于每组测试数据，请输出一个整数和一个浮点数；
其中整数表示解药的最大体积，浮点数表示解药的浓度(四舍五入保留2位小数)；
如果不能配出满足要求的的解药，则请输出0 0.00。

Sample

Inputcopy	Outputcopy
3 1 100 10 100 2 100 24 20 30 3 100 24 20 20 30	0 0.00 100 0.20 300 0.23

Hint 

排序各药水浓度从低到高，不断累加各个药水，一旦浓度大于W，立即退出 

#include
#include 
#include
using namespace std;
const int N = 100;
int a[N];
int main()
{
    int t, n, v, w;
    scanf("%d", &t);
    while(t--) {
        scanf("%d%d%d", &n, &v, &w);
        for(int i = 0; i < n; i++) scanf("%d", &a[i]);
        sort(a, a + n);
        if(a[0] > w) printf("0 0.00\n");
        else {
            double ans = 0, sum = 0;
            int cnt = 0;
            for(int i = 0; i < n; i++) {
                sum += a[i] * v;
                if(sum / (v * (i + 1)) <= w) {//确保药水浓度一定小于等于W
                    ans = sum / (v * (i + 1));
                    cnt++;
                } else break;
            }
            printf("%d %.2f\n", cnt * v, ans / 100);
        }
    }

    return 0;
}

G - 国王游戏

Description

恰逢 H 国国庆，国王邀请 n 位大臣来玩一个有奖游戏。首先，他让每个大臣在左、右手上面分别写下一个整数，国王自己也在左、右手上各写一个整数。然后，让这 n 位大臣排成一排，国王站在队伍的最前面。排好队后，所有的大臣都会获得国王奖赏的若干金币，每位大臣获得的金币数分别是：排在该大臣前面的所有人的左手上的数的乘积除以他自己右手上的数，然后向下取整得到的结果。

国王不希望某一个大臣获得特别多的奖赏，所以他想请你帮他重新安排一下队伍的顺序，使得获得奖赏最多的大臣，所获奖赏尽可能的少。注意，国王的位置始终在队伍的最前面。

Input

第一行包含一个整数 n，表示大臣的人数。

第二行包含两个整数 a 和 b，之间用一个空格隔开，分别表示国王左手和右手上的整数。

接下来 n 行，每行包含两个整数 a 和 b，之间用一个空格隔开，分别表示每个大臣左手和右手上的整数。

Output

一个整数，表示重新排列后的队伍中获奖赏最多的大臣所获得的金币数。

Sample 1

Inputcopy	Outputcopy
3 1 1 2 3 7 4 4 6	2

Hint

【输入输出样例说明】

按 11、22、33 这样排列队伍，获得奖赏最多的大臣所获得金币数为 22；

按 11、33、22 这样排列队伍，获得奖赏最多的大臣所获得金币数为 22；

按 22、11、33 这样排列队伍，获得奖赏最多的大臣所获得金币数为 22；

按22、33、11这样排列队伍，获得奖赏最多的大臣所获得金币数为 99；

按 33、11、22这样排列队伍，获得奖赏最多的大臣所获得金币数为 22；

按33、22、11 这样排列队伍，获得奖赏最多的大臣所获得金币数为 99。

因此，奖赏最多的大臣最少获得 22 个金币，答案输出 22。

HINT

贪心的去考虑，对于每个大臣 i 和 i+1 ，他们是否要交换的条件是什么

如果 i 放在 i + 1 前面 那么他们获得的金币是

sum * ai-1 / bi sum * ai-1 * ai /bi+1

反之

sum * ai-1 / bi+1 sum * ai-1 * ai+1 /bi

约去相同的

1 / bi 1 * ai /bi+1

1 / bi+1 1 ai+1 /bi

那么只要交换的条件就是

ai /bi+1 > ai+1 /bi

交换位置就可以得到

ai * bi > ai+1 * ai+1 /bi

由于最大值会很大所以要用高精度                                    ...不太懂这题下面是复制的代码-.-

#include 
using namespace std;
int n;
struct data
{
     int a, b;
} t[10005];
int cmp(data a, data b) { return a.a * a.b < b.a * b.b; }
int res[20005];
string multi(string p, string q)
{
      reverse(p.begin(), p.end());
      reverse(q.begin(), q.end());
      memset(res, 0, sizeof res);
      for (int i = 0; i < p.size(); i++)
      {
           for (int j = 0; j < q.size(); j++)
           {
                res[i + j] += (p[i] - '0') * (q[j] - '0');
           }
      }
     for (int i = 0; i < p.size() + q.size(); i++)
     {
         if (res[i] >= 10)
         {
             res[i + 1] += res[i] / 10;
             res[i] %= 10;
         }
     }
     string restr = "";
     bool fg = 1;
     for (int i = p.size() + q.size() - 1; i >= 0; i--)
     {
          if (res[i] == 0 && fg)
              continue;
          else
          {
              fg = 0;
              restr += res[i] + '0';
          }
     }
     return restr;
}
string mx(string p, string q)
{
       if (p.size() != q.size())
           return p.size() > q.size() ? p : q;
       return p > q ? p : q;
}
int dvs[20005], dvres[20005];
string div(string a, int b)
{
      memset(dvs, 0, sizeof(dvs));
      memset(dvres, 0, sizeof(dvres));
      for (int i = 0; i < a.size(); i++)
          dvs[i + 1] = a[i] - '0';
      int bs = 0;
      for (int i = 1; i <= a.size(); i++)
      {
           dvres[i] = (bs * 10 + dvs[i]) / b;
           bs = (bs * 10 + dvs[i]) % b;
      }
      int lc = 1;
      while (dvres[lc] == 0 && lc < a.size())
             ++lc;
      string div_ans = "";
      for (int i = lc; i <= a.size(); i++)
             div_ans += dvres[i] + '0';
      return div_ans;
}
string to_str(int qs)
{
       string p_ans = "";
       while (qs)
       {
           p_ans += qs % 10 + '0';
           qs /= 10;
       }
       reverse(p_ans.begin(), p_ans.end());
       return p_ans;
}
int main()
{
     scanf("%d", &n);
     for (int i = 0; i <= n; i++)
          scanf("%d%d", &t[i].a, &t[i].b);
     sort(t + 1, t + n + 1, cmp);
     string ans = "0", mul = to_str(t[0].a);
     for (int i = 1; i <= n; i++)
     {
          ans = mx(ans, div(mul, t[i].b));
          mul = multi(mul, to_str(t[i].a));
     }
     cout << ans << endl;
     return 0;
}

H - 跳跳

Description

你是一只小跳蛙，你特别擅长在各种地方跳来跳去。

这一天，你和朋友小 F 一起出去玩耍的时候，遇到了一堆高矮不同的石头，其中第 i 块的石头高度为 hi​，地面的高度是 h0​=0。你估计着，从第 i 块石头跳到第 j 块石头上耗费的体力值为(hi​−hj​)^2，从地面跳到第 i 块石头耗费的体力值是 (hi​)^2。

为了给小 F 展现你超级跳的本领，你决定跳到每个石头上各一次，并最终停在任意一块石头上，并且小跳蛙想耗费尽可能多的体力值。

当然，你只是一只小跳蛙，你只会跳，不知道怎么跳才能让本领更充分地展现。

不过你有救啦！小 F 给你递来了一个写着 AK 的电脑，你可以使用计算机程序帮你解决这个问题，万能的计算机会告诉你怎么跳。

那就请你——会写代码的小跳蛙——写下这个程序，为你 NOIp AK 踏出坚实的一步吧！

Input

输入一行一个正整数 n，表示石头个数。

输入第二行 n 个正整数，表示第 i 块石头的高度 hi​。

Output

输出一行一个正整数，表示你可以耗费的体力值的最大值。

Sample 1

Inputcopy	Outputcopy
2 2 1	5

Sample 2

Inputcopy	Outputcopy
3 6 3 5	49

Hint

样例解释

两个样例按照输入给定的顺序依次跳上去就可以得到最优方案之一。

HINT 

排列，然后用双指针 

#include
using namespace std;
long long  n;
long long  a[320];
signed main(){
	ios::sync_with_stdio(false);cin.tie(0);
	cin>>n;
	for(long long  i=1;i<=n;i++)	cin>>a[i]; 
	sort(a+1,a+n+1);
	long long i=0,j=n,ans=0;//i从0开始，从地面跳到最高的石头
	while(i

I -  三国游戏

Description

小涵很喜欢电脑游戏，这些天他正在玩一个叫做《三国》的游戏。

在游戏中，小涵和计算机各执一方，组建各自的军队进行对战。游戏中共有 N 位武将（N为偶数且不小于44），任意两个武将之间有一个“默契值”，表示若此两位武将作为一对组合作战时，该组合的威力有多大。游戏开始前，所有武将都是自由的（称为自由武将，一旦某个自由武将被选中作为某方军队的一员，那么他就不再是自由武将了），换句话说，所谓的自由武将不属于任何一方。

游戏开始，小涵和计算机要从自由武将中挑选武将组成自己的军队，规则如下：小涵先从自由武将中选出一个加入自己的军队，然后计算机也从自由武将中选出一个加入计算机方的军队。接下来一直按照“小涵→计算机→小涵→……”的顺序选择武将，直到所有的武将被双方均分完。然后，程序自动从双方军队中各挑出一对默契值最高的武将组合代表自己的军队进行二对二比武，拥有更高默契值的一对武将组合获胜，表示两军交战，拥有获胜武将组合的一方获胜。

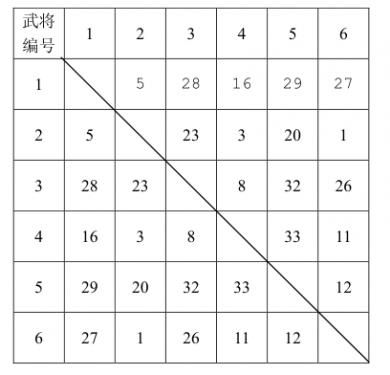
已知计算机一方选择武将的原则是尽量破坏对手下一步将形成的最强组合，它采取的具体策略如下：任何时刻，轮到计算机挑选时，它会尝试将对手军队中的每个武将与当前每个自由武将进行一一配对，找出所有配对中默契值最高的那对武将组合，并将该组合中的自由武将选入自己的军队。 下面举例说明计算机的选将策略，例如，游戏中一共有66个武将，他们相互之间的默契值如下表所示：

双方选将过程如下所示：

小涵想知道，如果计算机在一局游戏中始终坚持上面这个策略，那么自己有没有可能必胜？如果有，在所有可能的胜利结局中，自己那对用于比武的武将组合的默契值最大是多少？

假设整个游戏过程中，对战双方任何时候均能看到自由武将队中的武将和对方军队的武将。为了简化问题，保证对于不同的武将组合，其默契值均不相同。

Input

共 N 行。

第一行为一个偶数 N，表示武将的个数。

第 22行到第 N行里，第i+1行有Ni​个非负整数，每两个数之间用一个空格隔开，表示i号武将和i+1,i+2,…,N号武将之间的默契值（0≤默契值0≤1,000,000,000）。

Output

共一或二行。

若对于给定的游戏输入，存在可以让小涵获胜的选将顺序，则输出1，并另起一行输出所有获胜的情况中，小涵最终选出的武将组合的最大默契值。如果不存在可以让小涵获胜的选将顺序，则输出 0。

Sample 1

Inputcopy	Outputcopy
6 5 28 16 29 27 23 3 20 1 8 32 26 33 11 12	1 32

Sample 2

Inputcopy	Outputcopy
8 42 24 10 29 27 12 58 31 8 16 26 80 6 25 3 36 11 5 33 20 17 13 15 77 9 4 50 19	1 77

HINT 

P1199 [NOIP2010 普及组] 三国游戏 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

题解讲得很详细

#include
#define ll long long
using namespace std;
ll s[520][520],ans,n;
int main()
{
	ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		for(int j=i+1;j<=n;j++)
		{
			cin>>s[i][j];
			s[j][i]=s[i][j];//建表沿对角线对称的表 
		}
	}
	for(int i=1;i<=n;i++)
	{
		sort(s[i]+1,s[i]+n+1);//排序
		ans=max(ans,s[i][n-1]);//找第二大的值
	}
	cout<<"1"<

J - Diong Homework Again

Ignatius has just come back school from the 30th ACM/ICPC. Now he has a lot of homework to do. Every teacher gives him a deadline of handing in the homework. If Ignatius hands in the homework after the deadline, the teacher will reduce his score of the final test. And now we assume that doing everyone homework always takes one day. So Ignatius wants you to help him to arrange the order of doing homework to minimize the reduced score.

Input

The input contains several test cases. The first line of the input is a single integer T that is the number of test cases. T test cases follow.
Each test case start with a positive integer N(1<=N<=1000) which indicate the number of homework.. Then 2 lines follow. The first line contains N integers that indicate the deadlines of the subjects, and the next line contains N integers that indicate the reduced scores.

Output

For each test case, you should output the smallest total reduced score, one line per test case.

Sample

Inputcopy	Outputcopy
3 3 3 3 3 10 5 1 3 1 3 1 6 2 3 7 1 4 6 4 2 4 3 3 2 1 7 6 5 4	0 3 5

#include 
#include
using namespace std;
const int N = 1005;
struct Node {
    int deadline, score;
} a[N];
int vis[N];
bool cmp(Node a, Node b)
{
    return a.score == b.score ? a.deadline < b.deadline : a.score > b.score;
}
int main()
{
    int t, n;
    scanf("%d", &t);
    while (t--) {
        scanf("%d", &n);
        for (int i = 0; i < n; i++) scanf("%d", &a[i].deadline);
        for (int i = 0; i < n; i++) scanf("%d", &a[i].score); 
        sort(a, a + n, cmp);
        memset(vis, 0, sizeof vis);
        int sum = 0;
        for (int i = 0; i < n; i++) {
            int j;
            for (j = a[i].deadline; j > 0; j--)
                if (vis[j] == 0) {
                    vis[j] = 1;//完成作业
                    break;
                }
            if (j == 0) sum += a[i].score; //没完成作业被扣的分
        }
        printf("%d\n", sum);
    }
    return 0;
}

K - Hero

When playing DotA with god-like rivals and pig-like team members, you have to face an embarrassing situation: All your teammates are killed, and you have to fight 1vN.

There are two key attributes for the heroes in the game, health point (HP) and damage per shot (DPS). Your hero has almost infinite HP, but only 1 DPS.

To simplify the problem, we assume the game is turn-based, but not real-time. In each round, you can choose one enemy hero to attack, and his HP will decrease by 1. While at the same time, all the lived enemy heroes will attack you, and your HP will decrease by the sum of their DPS. If one hero's HP fall equal to (or below) zero, he will die after this round, and cannot attack you in the following rounds.

Although your hero is undefeated, you want to choose best strategy to kill all the enemy heroes with minimum HP loss.

Input

The first line of each test case contains the number of enemy heroes N (1 <= N <= 20). Then N lines followed, each contains two integers DPSi and HPi, which are the DPS and HP for each hero. (1 <= DPSi, HPi <= 1000)

Output

Output one line for each test, indicates the minimum HP loss.

Sample

Inputcopy	Outputcopy
1 10 2 2 100 1 1 100	20 201

 HINT

创建敌人的结构体包括DPS（攻击力）,HP（血量），VIP（先攻击的排序） ，需要注意的是每轮丢失的血量是在场所有存活敌人造成的伤害总值

#include
#include
#include
using namespace std;
struct node{
  int hp,dps;//dps:伤害 hp:血量
  double vip;
  friend bool operator < (node a,node b){
      return a.vip < b.vip;
  }
};
int main(void)
{
  int n;
  while(scanf("%d",&n) != EOF){
    priority_queue q;
    node v;
    int cnt = 0,count = 0;
    while(n--){
      scanf("%d %d",&v.dps,&v.hp);
      v.vip = (double)(v.dps)/(double)(v.hp);
      count += v.dps;
      q.push(v);
    }
    while(!q.empty()){
      v = q.top();
      cnt += (count * v.hp);
      count -= v.dps;
      q.pop();
    }
    printf("%d\n",cnt);
  }
  return 0;
}

#include 
#include 
#include 
using namespace std;
struct enemies {
    int DPS;
    int HP;
	double s; //sequence
} a[25];
bool cmp(enemies a, enemies b)
{
    return a.s> b.s;
}
int main()
{
    int n;
    while(~scanf("%d",&n)){
    	memset(a, 0, sizeof(a));
    	for(int i=0;i

 L - 凌乱的 yyy / 线段覆盖

Background

快 noip 了，yyy 很紧张！

Description

现在各大 oj 上有 n 个比赛，每个比赛的开始、结束的时间点是知道的。

yyy 认为，参加越多的比赛，noip 就能考的越好（假的）。

所以，他想知道他最多能参加几个比赛。

由于 yyy 是蒟蒻，如果要参加一个比赛必须善始善终，而且不能同时参加 22 个及以上的比赛。

Input

第一行是一个整数 n，接下来 n 行每行是 2 个整数 ai​,bi​ (ai​

Output

一个整数最多参加的比赛数目。

Sample 1

Inputcopy	Outputcopy
3 0 2 2 4 1 3	2

#include
using namespace std;
const int N=1e6+5;
struct act{
	int strat;
	int end;
}a[N];
bool cmp(act a,act b){
	return a.end >n; 
	for(int i=0;i>a[i].strat >> a[i].end; 
	}
    sort(a,a+n,cmp);
    int x=1,e=a[0].end ;
    for(int i=1;i=e){
    		x++;
    		e=a[i].end ;
		}
	}
	cout<

M - 删数问题

Description

键盘输入一个高精度的正整数 N（不超过 250 位），去掉其中任意 k 个数字后剩下的数字按原左右次序将组成一个新的非负整数。编程对给定的 N 和 k，寻找一种方案使得剩下的数字组成的新数最小。

Input

输入两行正整数。

第一行输入一个高精度的正整数 n。

第二行输入一个正整数 k，表示需要删除的数字个数。

Output

输出一个整数，最后剩下的最小数。

Sample 1

Inputcopy	Outputcopy
175438 4	13

 HINT

每次删除的数是从左往右开始遍历，第一个比右边位大的数 

#include
#include
using namespace std;
char s[300];
int a[300],x,k;
int main(){
	cin>>s>>x;
	int n=strlen(s);
	for(int i=0;ia[j+1]){
		    	for(int k=j;k