博弈论学习笔记(3)——完全信息动态博弈
前言
在这个部分,我们学习的是完全信息动态博弈。主要内容包括扩展式博弈、子博弈精炼Nash均衡、重复博弈和子博弈精炼Nash均衡的应用。
一、扩展式博弈
1、扩展式博弈
1)扩展式博弈是什么
扩展式博弈是博弈问题的一种规范性描述,扩展式博弈注重对参与人在博弈过程中所遇到决策问题的序列结构的详细分析。
2)扩展式博弈包含的要素
3)博弈树是什么
博弈树是扩展式博弈中简单直观的一种描述方式。其由结和有向枝构成。
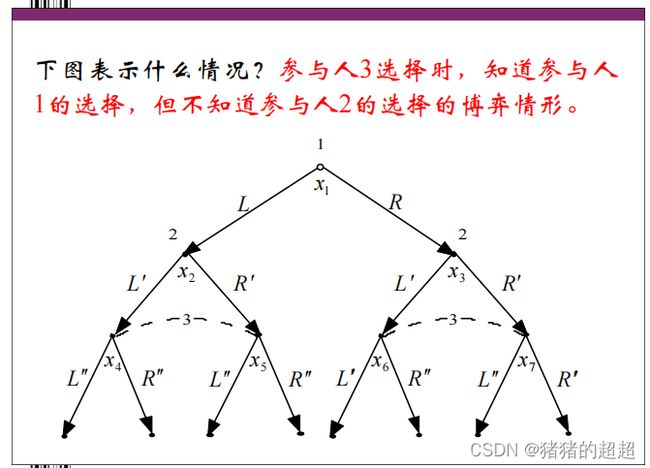
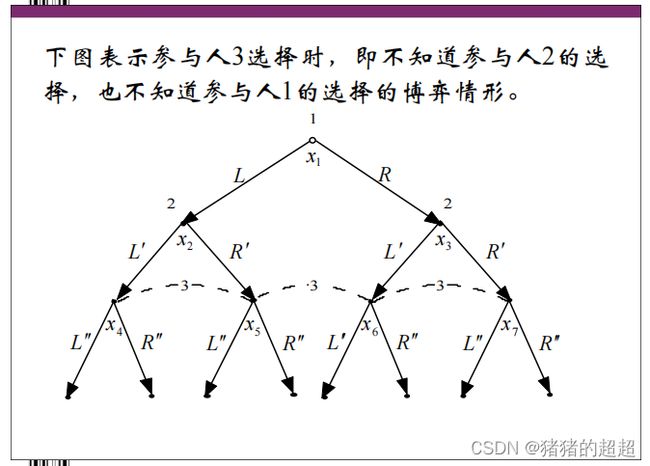
4)信息集是什么
对于信息集的描述,注意区分以下三种情况:
5)完美记忆是什么
2、扩展式博弈的战略及其Nash均衡
1)扩展式博弈中的战略
参与人的战略就是参与人在博弈中的行动规则,它规定了参与人在博弈中每一种轮到自己行动的情形下,应该采取的行动。而在博弈树中,参与人在博弈中每一种轮到自己行动的情形又可以用一个信息集来表示,因此,参与人在扩展式博弈中的战略实际上就是参与人在每个信息集上的行动规则。
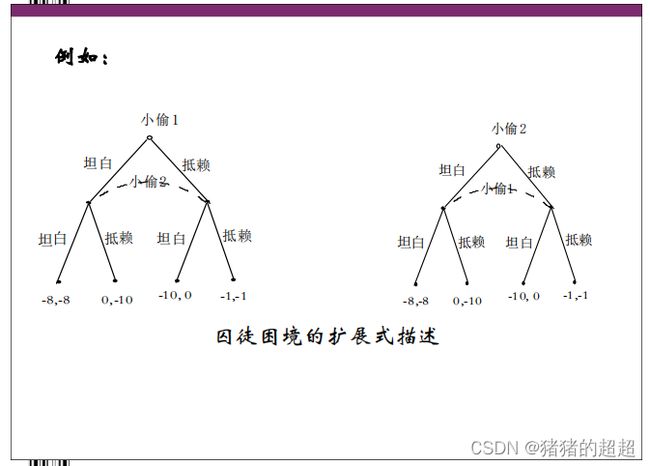
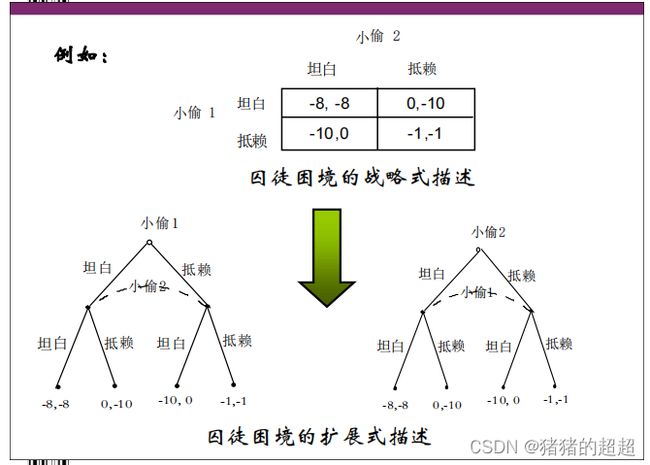
2)由扩展式描述得到战略式描述
![]()
3、战略式博弈 VS 扩展式博弈
1)战略式博弈本质上是静态模型
战略式假设所有的参与人同时选择战略并得到博弈的结果,至于博弈中参与人何时行动、行动时又如何行动等等,战略式博弈并不考虑。
2)扩张式博弈本质上是动态模型
-
扩展式博弈不仅直观地给出了博弈的结果,而且还对博弈的过程进行详尽的描述。
-
可以给出博弈中参与人的行动顺序,以及参与人行动时的决策环境和行动空间。
3)两种博弈描述形式的比较
-
给出博弈问题的扩展式描述(如博弈树),我们就可得到博弈问题的战略式描述。
-
给出博弈问题的战略式描述,我们也能构造出博弈问题的扩展式描述。
二、子博弈精炼Nash均衡
1、子博弈精炼Nash均衡
1)将Nash均衡作为扩展式博弈的解会有什么问题
Nash均衡是一个静态均衡,将Nash均衡作为扩展式博弈的解同样会遇到Nash均衡的多重性问题,而且在多个Nash均衡中有些明显不合理。
2)子博弈的概念
-
子博弈就是原博弈的一部分,它始于原博弈中一个位于单结信息集中的决策结 X ,并由决策结 X 及其后续结共同组成。
-
子博弈可以作为一个独立的博弈进行分析,并且与原博弈具有相同的信息结构。
3)子博弈精炼Nash均衡的定义
4)Kuhn定理
每个有限的扩展式博弈都存在子博弈精炼Nash均衡。
虽然Kuhn定理保证了子博弈精炼Nash均衡的存在性,但Kuhn定理并不能确保我们所讨论的有限的扩展式博弈都只存在惟一的子博弈精炼Nash均衡。
5)解的多重性问题
2、子博弈精炼Nash均衡的求解
1)求解有限扩展式博弈的一般步骤
-
找出博弈的所有子博弈;
-
按照博弈进程的“反方向”逐一求解各个子博弈,即最先求解最底层的子博弈,再求解上一层的子博弈,......,直至原博弈。也就是说,在求解每一个子博弈时,该子博弈要么不含有其它任何子博弈,要么所含子博弈都已被求解。
2)逆向归纳法
3)完美信息与完全信息
4)子博弈精炼Nash均衡 VS Nash均衡
3、承诺行动与要挟诉讼
1)承诺行动
承诺行动就是在博弈开始之前参与人采取的某种改变自己支付或行动空间的行动,该行动可使原本不可信的威胁变得可信。
-
在许多情况下,承诺行动对参与人来讲是有利的,因为它能使博弈的精炼均衡发生有利于自己的改变。
-
需要注意的是,参与人的承诺行动是有成本的(沉没成本),否则这种承诺就不可信。
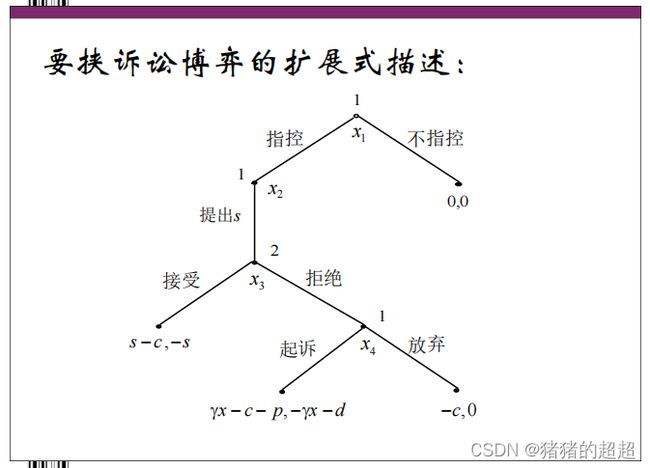
2)要挟诉讼
所谓要挟诉讼是指那种原告几乎不可能胜诉而其惟一的目的可能是希望通过私了得到一笔赔偿的诉讼。
博弈的结果似乎与人们观测到的现实并不相符,因为现实中人们常常看到各种“要挟”的发生。在上述模型中,“要挟”之所以没有成果,关键在于原告将会起诉的威胁并不可信。
原告需要采取承诺行动,来使自己的威胁变得可信。
具体的扩展式博弈过程详见PPT。
4、子博弈精炼Nash均衡的合理性讨论
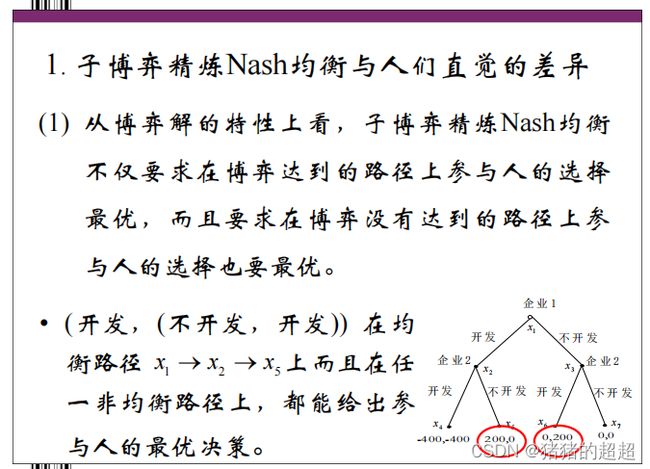
1)与人们直觉的差异
2)逆向归纳法对理性的要求
如同前面所定义的博弈的解一样,子博弈精炼Nash均衡不仅要求“参与人完全理性”,而且要求“参与人完全理性”为共同知识,否则就无法使用逆向归纳法求解子博弈精炼Nash均衡。
三、重复博弈
1、有限重复博弈
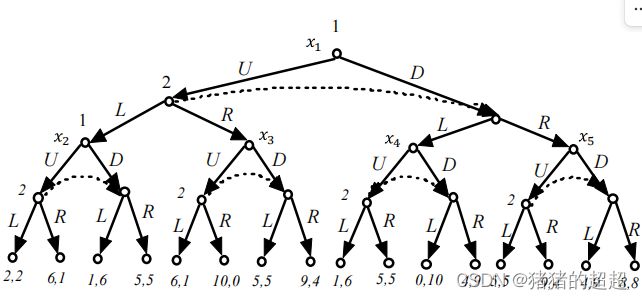
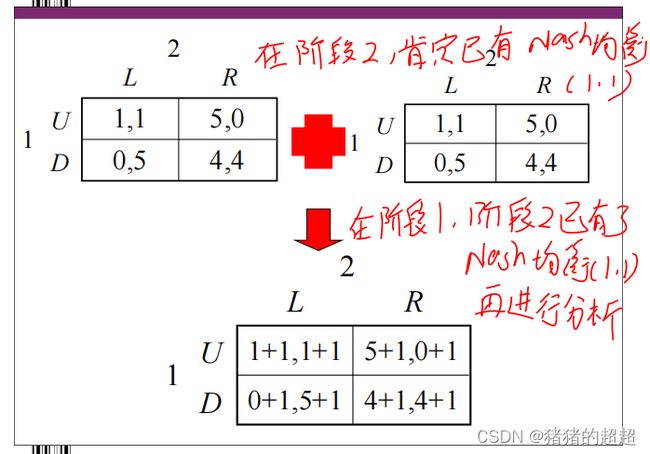
1)重复博弈的例子
多阶段的动态博弈,在博弈的每个阶段,重复同样的博弈。重复博弈关心的是将来可信的威胁或承诺如何影响到当前的行动。
2)重复博弈的定义
3)重复博弈的特征
4)有限重复博弈解唯一性定理
5)触发策略
明确触发策略的定义,掌握触发策略的构造
在博弈论中,触发策略(Trigger Strategy)是指参与者在多次博弈中如何作出决策的一种策略。它基于一个前提条件,即当某个事件或信号(触发器)被触发时,参与者会采取特定的行动。
具体来说,触发策略通常用于描述在重复博弈中的行为模式。在这种情况下,每个参与者可以选择在每轮博弈中采取不同的策略。触发策略则是一种基于触发事件的约定,一旦触发事件发生,所有参与者都会采取预定的行动,而无需重新计算和选择策略。
触发策略的关键是确定触发事件以及参与者对该事件的响应。触发事件可以是其他参与者的特定行动、某种外部环境变化或是达到某个特定的状态。一旦触发事件发生,参与者会根据预先确定的策略来采取行动,而不会再进行重新选择。
通过使用触发策略,参与者可以在博弈中建立可靠的合作或对抗方式,并相互约束对方的行为。触发策略可以为参与者提供稳定的行为模式和预期结果,从而降低信息不完全或不确定性所带来的影响。
总之,触发策略在博弈论中描述了参与者在多次博弈中如何根据特定事件或信号来作出决策的策略。它通过约定一旦触发事件发生,参与者会采取预先确定的行动,从而建立稳定的合作或对抗关系。
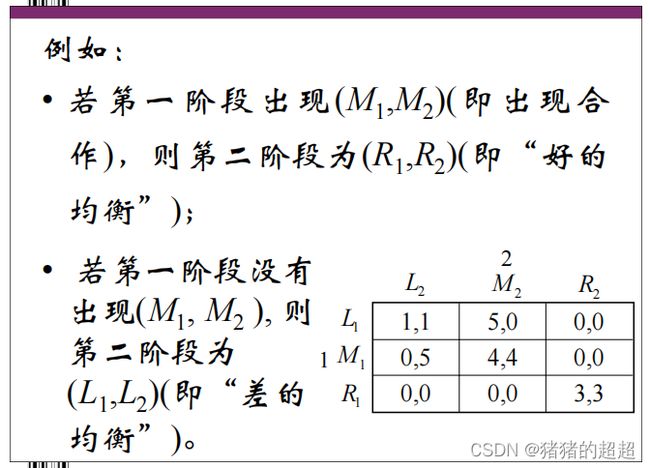
【例子】
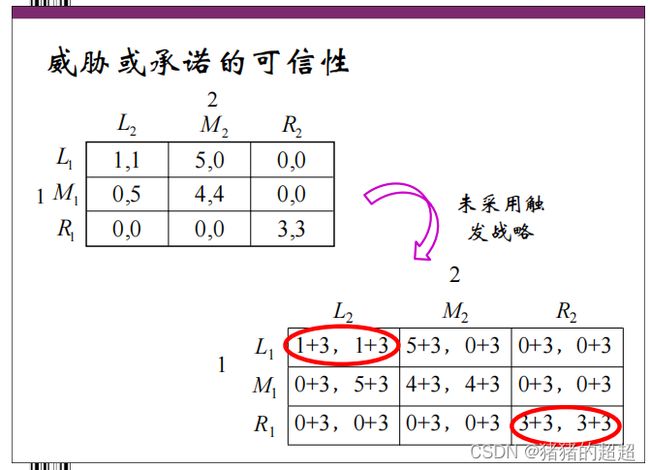
6)承诺或威胁的可信性
2、无限重复博弈
1)无限重复博弈的定义
2)无限重复博弈 VS 有限重复博弈
【二者的区别】
-
在有限重复博弈中,参与人在G(T)中的收益既可以是各阶段博弈收益的简单叠加,也可以是各阶段博弈收益的贴现;无限重复博弈中,参与人的收益只能是在无限次的阶段博弈中多的收益的贴现。
-
对于阶段博弈为上述博弈的有限重复博弈,合作不可能形成;但对于无限重复博弈,在一定的贴现率下,合作有可能形成。
3)贴现率的定义及计算
【贴现率的定义】
在博弈论中,贴现率(Discount Rate)是指用于对未来效用或收益进行折现(discounting)的利率。它是一个经济概念,用于衡量时间价值和风险的权衡。
在博弈论中,贴现率主要应用于序贯博弈(Sequential Games),其中参与者需要在不同的时间点做出决策。贴现率被用来对未来效用或收益进行折现,以反映人们在计算效用或收益时对时间的偏好和风险考虑。
具体来说,贴现率表示在将来获得的效用或收益相对于当前时刻的价值。较低的贴现率意味着人们更倾向于将未来的效用或收益视为更有价值,较高的贴现率意味着人们更倾向于将近期的效用或收益视为更有价值。
通过应用贴现率,人们可以将未来的效用或收益转化为等价的当前价值。这样可以使得不同时间点上的效用或收益可比较,从而帮助参与者做出决策。贴现率还可用于评估投资、项目选择以及对未来风险的考虑。
需要注意的是,贴现率是一个主观的概念,不同的个体或组织可能会有不同的贴现率,取决于其对时间价值和风险偏好的评估。在实际应用中,确定适当的贴现率通常需要考虑多种因素,如机会成本、市场利率、风险偏好等。
【贴现率的计算】
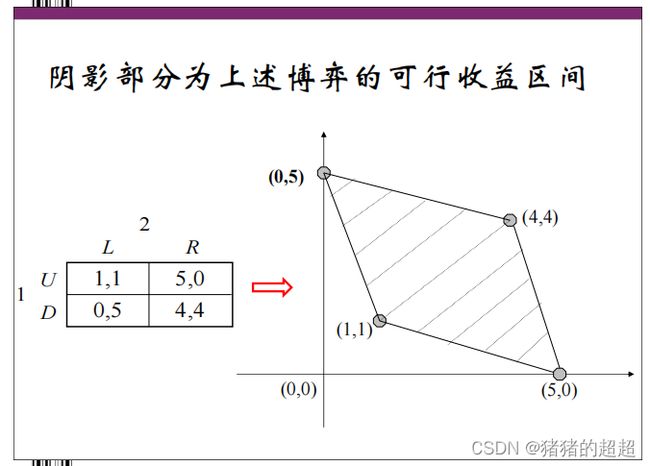
4)可行收益
5)平均收益
【提示】
左式为前T时间内的平均收益为 Π ,在贴现率为 δ 的情况下,T~2T时间内的预期收益为 δΠ ,2T~3T时间内的预期收益为 δ²Π ,那么无限重复博弈下收益为
Π+δΠ+δ²Π+...
右式为第1个单位时间内的收益为 Π1 ,第2个单位时间内的(虽然实际收益为 Π2 ,但要乘以贴现率)预期收益为 δΠ2,第3个单位时间内的预期收益为 δ²Π3 ,那么无限重复博弈下收益为
Π1+δΠ2+δ²Π3+···
二者均为无限重复博弈的收益,左式=右式,以此求得平均收益。
6)无名氏定理
【无名氏定理的意义】
在无限重复博弈中,任何一个Pareto有效的可行收益都可以通过一个特定的子博弈精炼Nash均衡得到
7)罗伯特·爱克斯罗德实验
最终,“一报还一报”的策略,赢得了游戏
四、子博弈精炼Nash均衡的应用
1、Stackelberg寡头竞争模型
1)经典案例
2)博弈过程
注意Stackelberg模型与Cournot模型的比较:产量、利润。
Stackelberg模型说明:
企业具有先动优势;
企业具有信息优势,反而使自己不利。
3)关于均衡结果的讨论
2、Leontief劳资谈判模型
1)经典案例
2)博弈过程
![]()
3、关税与国际市场
此题是大国税收博弈的推广, 由战略式博弈推广到扩展式博弈。
1)经典案例
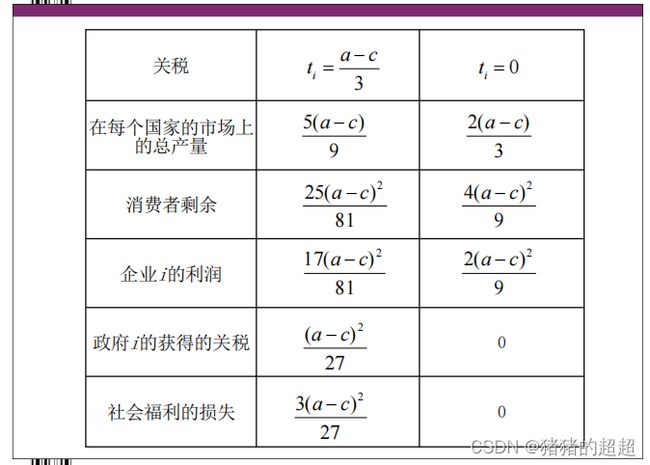
2)博弈过程
3)关于博弈结果的讨论
从上面的比较可以看出:关税的存在虽然会使政府的收益增加,但企业的收益和消费者剩余却会减少的更多,所以,非自由贸易会造成社会福利的损失。
4、投票次序效应
1)次序效应是什么
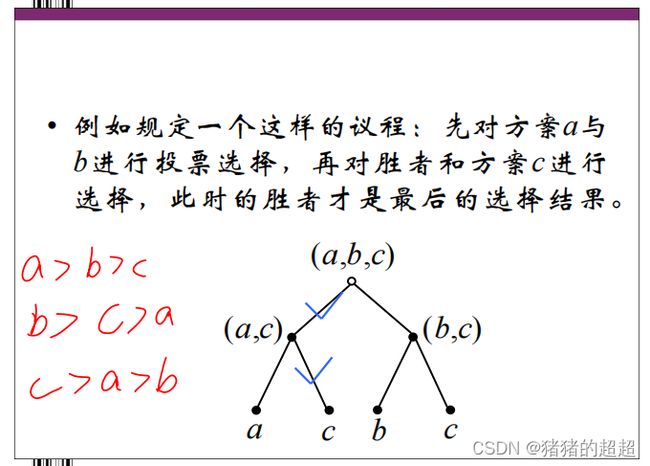
公共政策的选择都是按一定程序进行的。选择程序不同,选择结果就不同。但是,在某些情况下即使选择程序相同,而选择过程中方案的选择次序(即议程)不同,也会造成选择结果的极大差异。这种由于议程的不同而造成的选择结果的差异就是所谓的“次序效应”。在实际的公共政策选择过程中,“次序效应”普遍存在。
2)投票悖论
3)次序效应举例
上述由于议程的不同而造成的选择结果的差异,称之为“程序效应”(procedure effect)或“投票次序效应”(voting order effect,简称“次序效应”) 。
4)次序效应的结论
但是,上述结论是有条件的,它是在委员会中的各成员都根据自己的真实偏好进行投票的前提下得到的,也就是说,在投票过程中,对于每一轮投票各成员都是根据自己的偏好对方案进行选择,不能出现违背自己偏好的情形。
5)经典案例
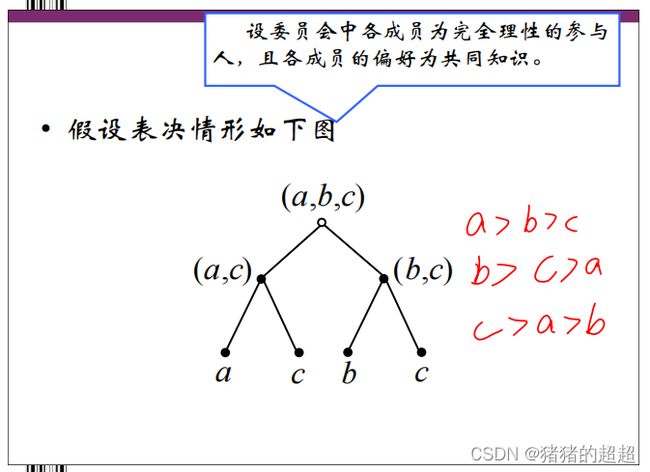
在实际的表决过程中,追求自身利益最大化的各成员不可能绝对地根据自己的真实偏好进行投票,尤其是当各成员相互知道对方偏好的时候。
6)博弈过程
7)关于博弈结果的讨论
在委员会偏好为共同知识的条件下,每个成员在第一轮投票中都是通过比较自己选择的后果来决定自己的选择,而并非完全根据自己的真实偏好进行选择。这说明委员会成员实际上是根据前面介绍过的“逆向递推”的原则(即逆向归纳法)来决定自己的选择。
8)投票次序效应的应用
在美国国会的政治斗争中,民主党和共和党不仅要在国会中争取更多的席位, 而且还要力争获得各个委员会尤其是程序委员会的控制权,其目的就是希望在议案的表决过程中,制定对自己最为有利的方案表决顺序(即议程)。
此外,由于委员会中成员偏好是否为共同知识,会对表决程序的“次序效应”产生完全不同的影响,因此,在投票表决之前是否需要对投入表决的方案进行公开、充分的辩论,各政党都会根据自身的利益进行通盘考虑。
总结
在这学期的博弈论课程中,我们主要学习的是完全信息静态博弈和完全信息动态博弈,需要掌握基本概念、明确Nash均衡的定义和求解,结合具体的案例进行分析。以上便是我们八周学习的课程,感谢大家的支持和鼓励~