c++ 实现二叉搜索树
二叉搜索树的概念
二叉搜索树 (BST,Binary Search Tree),也称二叉排序树或二叉查找树。它要么是一颗空树,要么是满足以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值。
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值。
- 它的左右子树也分别为二叉搜索树。
如上图,左侧的二叉树不是一颗二叉搜索树,右侧的二叉树是一颗二叉搜索树。
**为什么叫二叉搜索树(二叉查找树)呢?**因为二叉搜索树擅长搜索和查找。如下图的二叉搜索树,我们要查找 10,首先与根节点比较,10 大于 9,那么就去他的右子树查找。右子树的根节点为 13 大于 10,那么就去他的左子树查找。左子树的根节点为 10 刚好等于 10,查找成功!如果节点不存在那么就是查找到树的叶节点还没有找到目标节点。
理想状态下,二叉搜索树查找的时间复杂度为:O(logN)。但是理想很丰满,现实很骨干。有一种情况能使得二叉搜索树变成链表,从而使得查找的时间复杂度变为 O(N)。
如下图,当依次向一颗空的二叉搜索树中插入有序的节点。那么这颗二叉搜索树就会变成链表。
**为什么叫二叉排序树呢?**那是因为一颗二叉搜索树的中序遍历的结果是有序的!中序遍历就是在递归遍历二叉树的时候先访问左子树,在访问根节点,最后才是右子树。不会中序遍历不要紧,等我们实现了一颗二叉搜索树,中序遍历一次你就知道他为啥叫二叉排序树了!
二叉搜索树的实现
二叉搜索树的基本结构
定义二叉搜索树的基本结构:
- 首先,我们需要定义一个节点的类,表示二叉树的一个节点,成员变量就是左子树的节点指针,右子树的节点指针以及当前节点存储的值。构造函数的话,就是传入一个
key用来初始化节点的_key就行啦!指针全部初始化为nullptr。 - 然后就要定义二叉搜索树的类啦,里面会封装各种操作的函数。至于成员变量,当然就是根节点的指针啦!至于构造函数,一开始是一颗空的二叉搜索树嘛,将根节点的指针初始化为
nullptr就行啦!
template<class K>
struct BSTNode
{
BSTNode<K>* _left;
BSTNode<K>* _right;
K _key;
BSTNode(const K& key)
:_key(key)
,_left(nullptr)
,_right(nullptr)
{}
};
template<class K>
class BSTree
{
typedef BSTNode<K> Node;
public:
BSTree()
:_root(nullptr)
{}
private:
Node* _root;
};
bool insert(const K& key)
在我们实现的二叉搜索树中,一颗树中是没有相同节点的。
插入的过程其实很简单呢?将待插入的节点 key 与根节点的 _key 作比较:
- 如果待插入节点的 key 大于根节点的 _key,那么继续与右子树根节点的 _key 比较。
- 如果带插入节点的 key 小于根节点的 _key,那么继续与左子树根节点的 _key 比较。
- 如果遇到根节点为 nullptr,那么直接插入这个节点,从而完成二叉搜索树的插入操作。
bool insert(const K& key)
{
Node* newNode = new Node(key); //构造新插入的节点
if(_root == nullptr) //如果是一颗空的二叉搜索树,修改根节点就行了
{
_root = newNode;
}
else
{
Node* cur = _root; //新插入的节点每次都与 cur 比较,判断其插入位置
Node* parent = nullptr; //记录上父节点,方便最后的插入
while(cur)
{
if(key > cur->_key) //key 大于 cur->_key 去右子树
{
parent = cur;
cur = cur->_right;
}
else if(key < cur->_key) //key 小于 cur->_key 去左子树子树
{
parent = cur;
cur = cur->_left;
}
else //相等的情况不存在,我们规定二叉搜索树中不存在 _key 值相同的节点,插入失败
{
return false;
}
}
//确定插入的位置
if(key > parent->_key)
parent->_right = newNode;
else
parent->_left = newNode;
}
//插入成功
return true;
}
为了方便测试插入的结果是否正确,我们需要写一个中序遍历的函数,中序遍历在 C 语言阶段都是写过了的!忘记了的 uu 可以去复习复习。
C语言数据结构初阶(10)----二叉树的实现-CSDN博客
写成成员函数,通过类的对象调用,我们需要传参根节点的指针,但是这个成员变量是私有的!外面拿不到,你可以写一个函数获取根节点的指针,但是这里会有一个更加优雅的写法:
void inorder()
{
_inorder(_root);
cout << endl;
}
void _inorder(Node* root)
{
if(root == nullptr)
return;
_inorder(root->_left);
cout << root->_key << " ";
_inorder(root->_right);
}
中序遍历写好了,就方便我们测试一颗二叉树是不是二叉搜索树啦!二叉搜索树的中序遍历是有序的,中序遍历有序的树也是二叉搜索树。
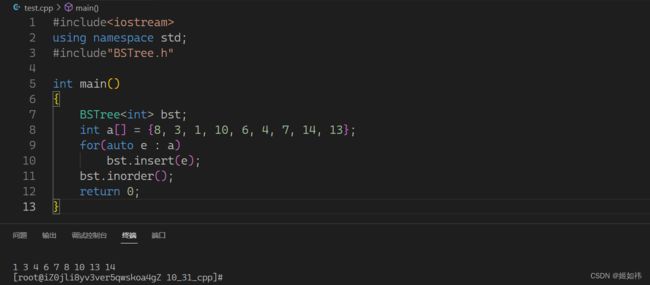
#include我们看到中序遍历的结果的确是有序的呢!那我们的插入函数就是没有问题的!
bool find(const K& key)
find 写起来比 insert 还简单哈!
- 如果待查找的 key 比根节点的 _key 大,那么就去右子树查找。
- 如果待查找的 key 比根节点的 _key 小,那么就去左子树查找。
- 如果待查找的 key 与根节点的 _key 相等,那么查找成功。
- 如果根节点为 nullptr 还没有查找成功,那么查找失败。
bool find(const K& key)
{
Node* cur = _root;
while(cur)
{
if(key > cur->_key)
cur = cur->_right;
else if(key < cur->_key)
cur = cur->_left;
else
return true;
}
return false;
}
void erase(const K& key)
erase 接口是二叉搜索树中最难实现的接口呢!
删除二叉搜索树中的节点可以分为以下情况:
-
如果删除节点的度为 0,即删除的节点没有左右孩子。那么直接删除这个节点,然后改变父节点指针的指向就可以啦!
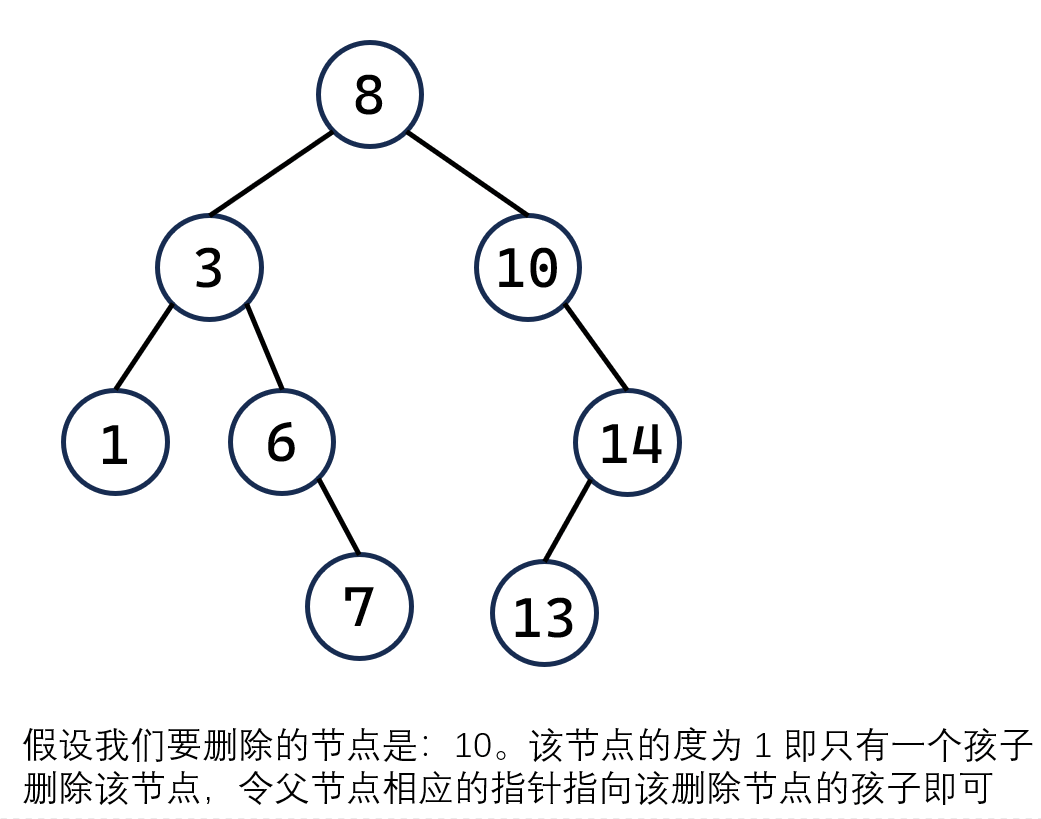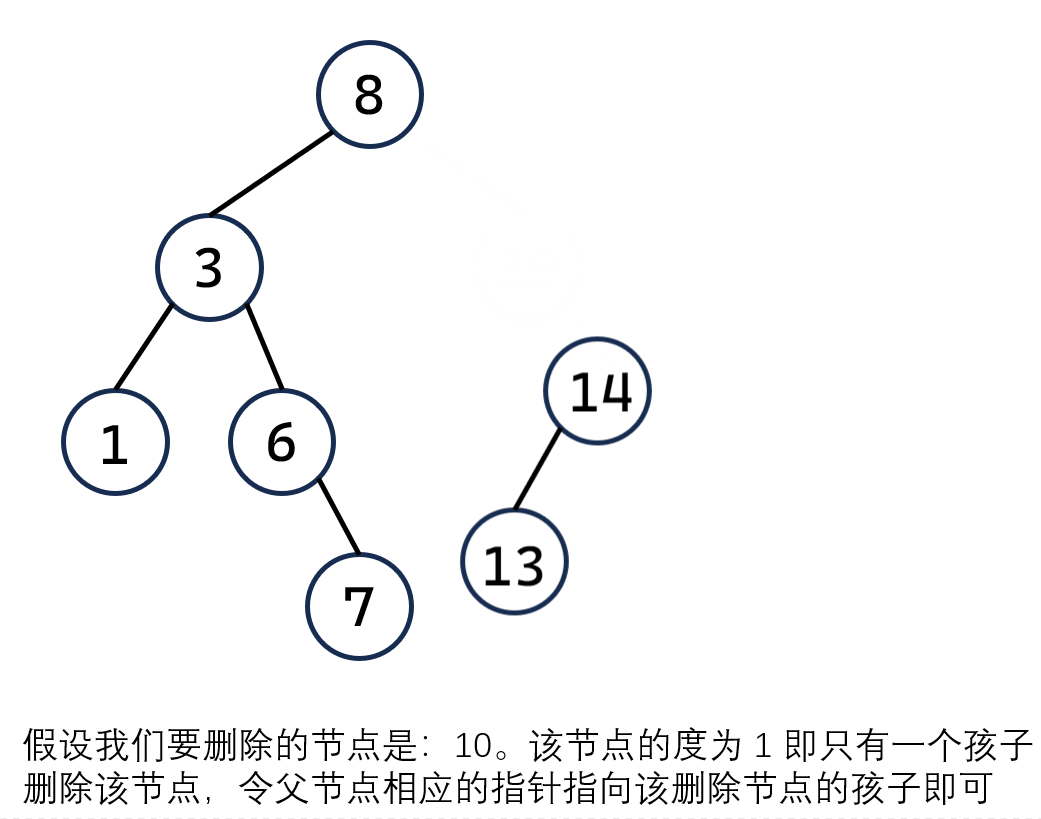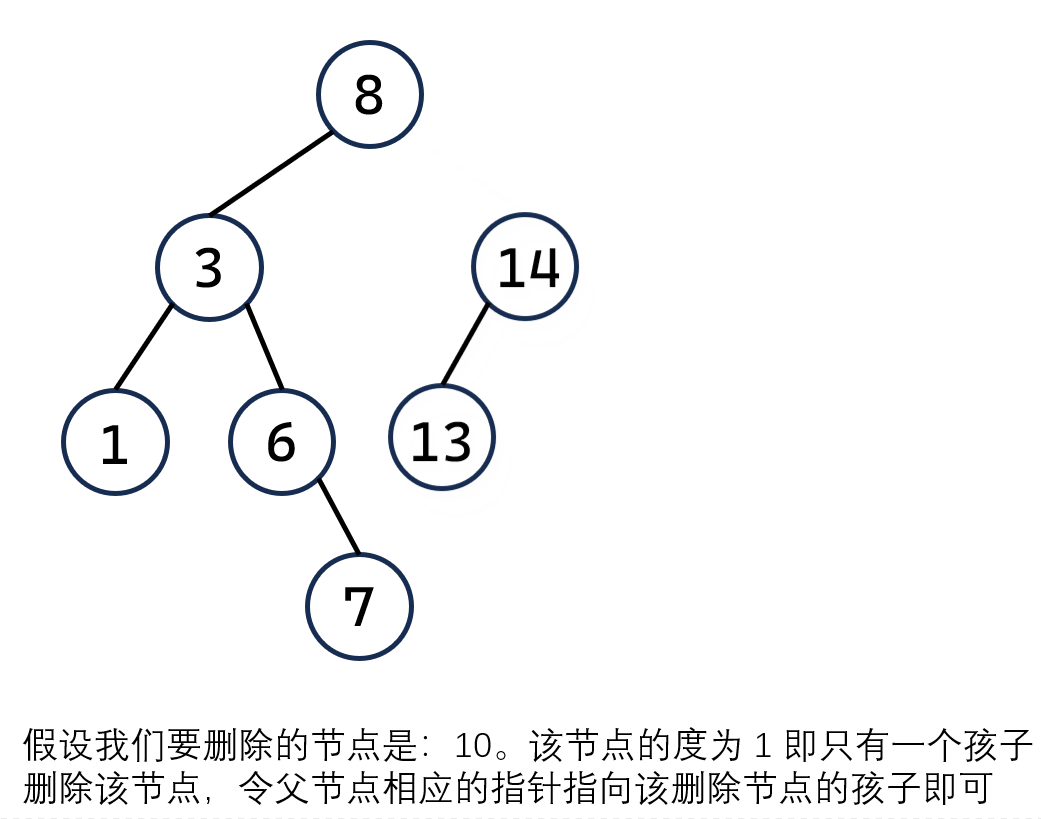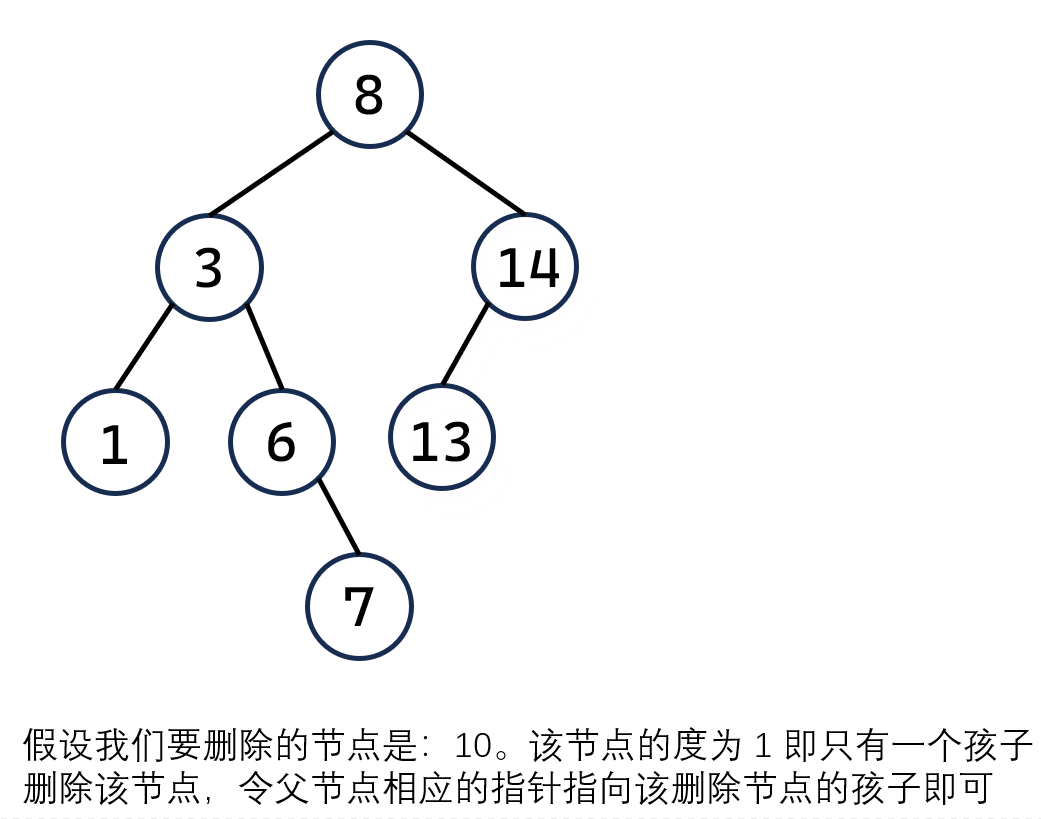
-
如果删除节点的度为 1,即删除的节点有一个孩子。那么,删除这个节点之后,令父节点相应的指针指向该删除节点的孩子即可。
什么是父节点的相应指针?
- 如果待删除的节点是其父节点的右孩子,那么删除这个节点之后,令父节点的
_right指针指向该删除节点的孩子即可。 - 如果待删除的节点是其父节点的左孩子,那么删除这个节点之后,令父节点的
_left指针指向该删除节点的孩子即可。
- 如果待删除的节点是其父节点的右孩子,那么删除这个节点之后,令父节点的
-
如果待删除节点的度为 2,即待删除的节点有两个孩子。此时我们选择使用替换法,即选择待删除节点的左右子树中的某一个节点来替代待删除节点的位置,最后删除那个被选择用来替代删除节点的节点即可!
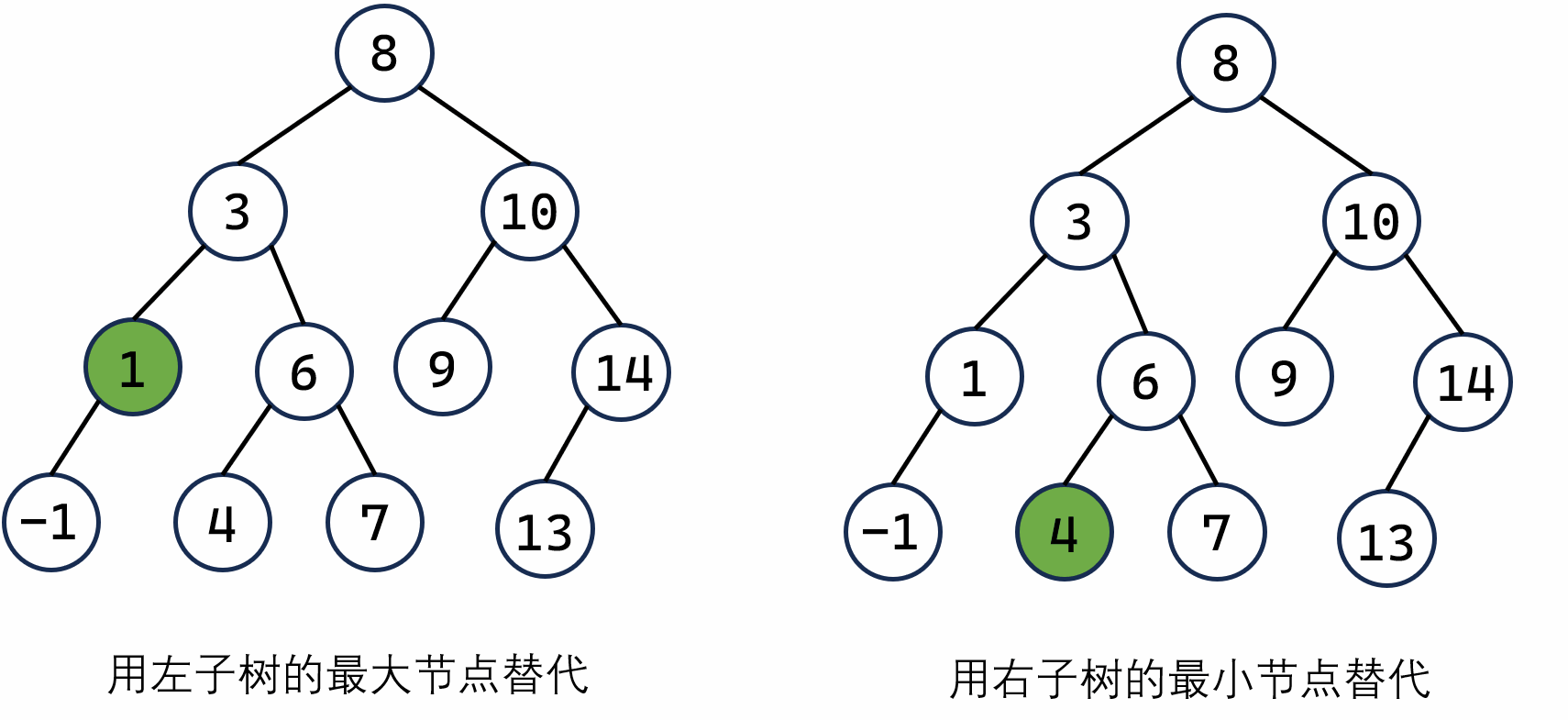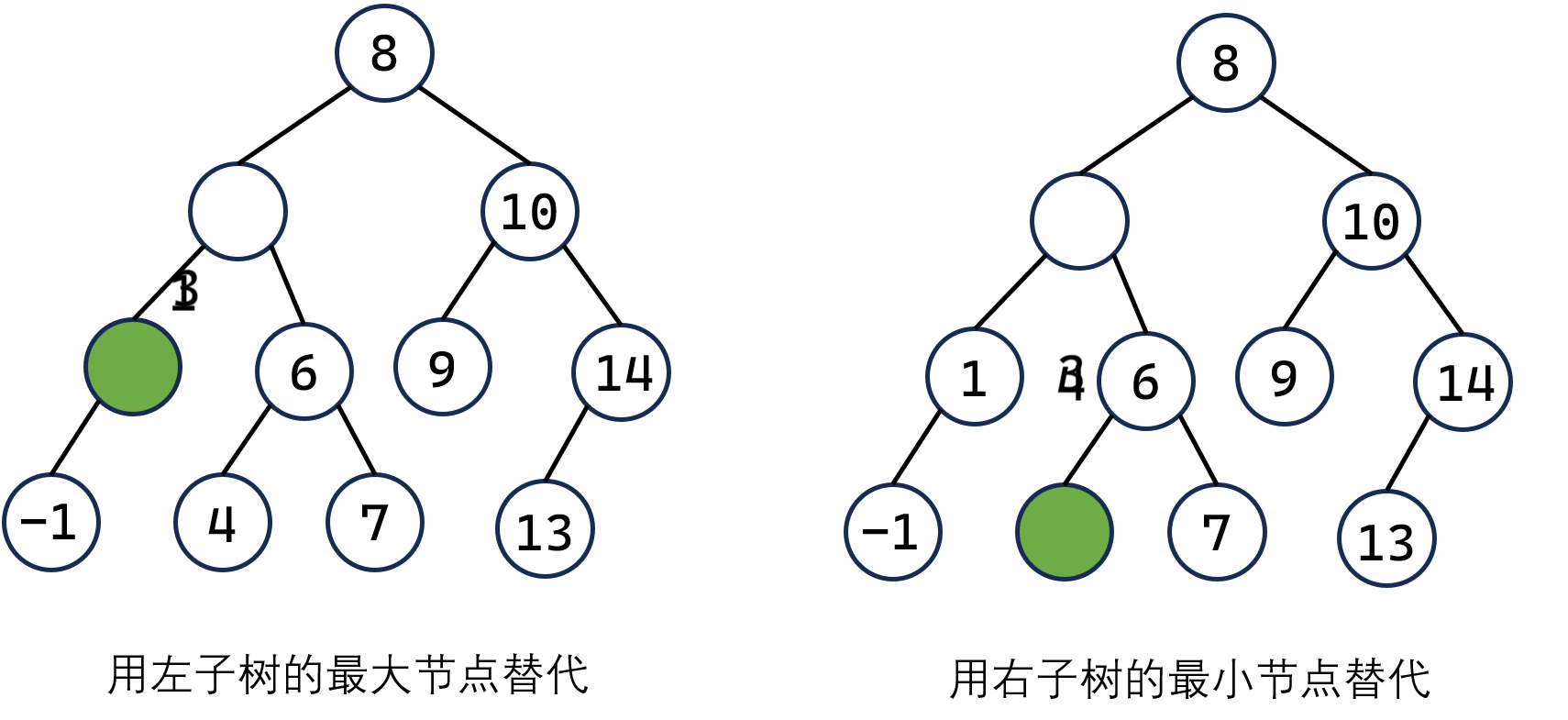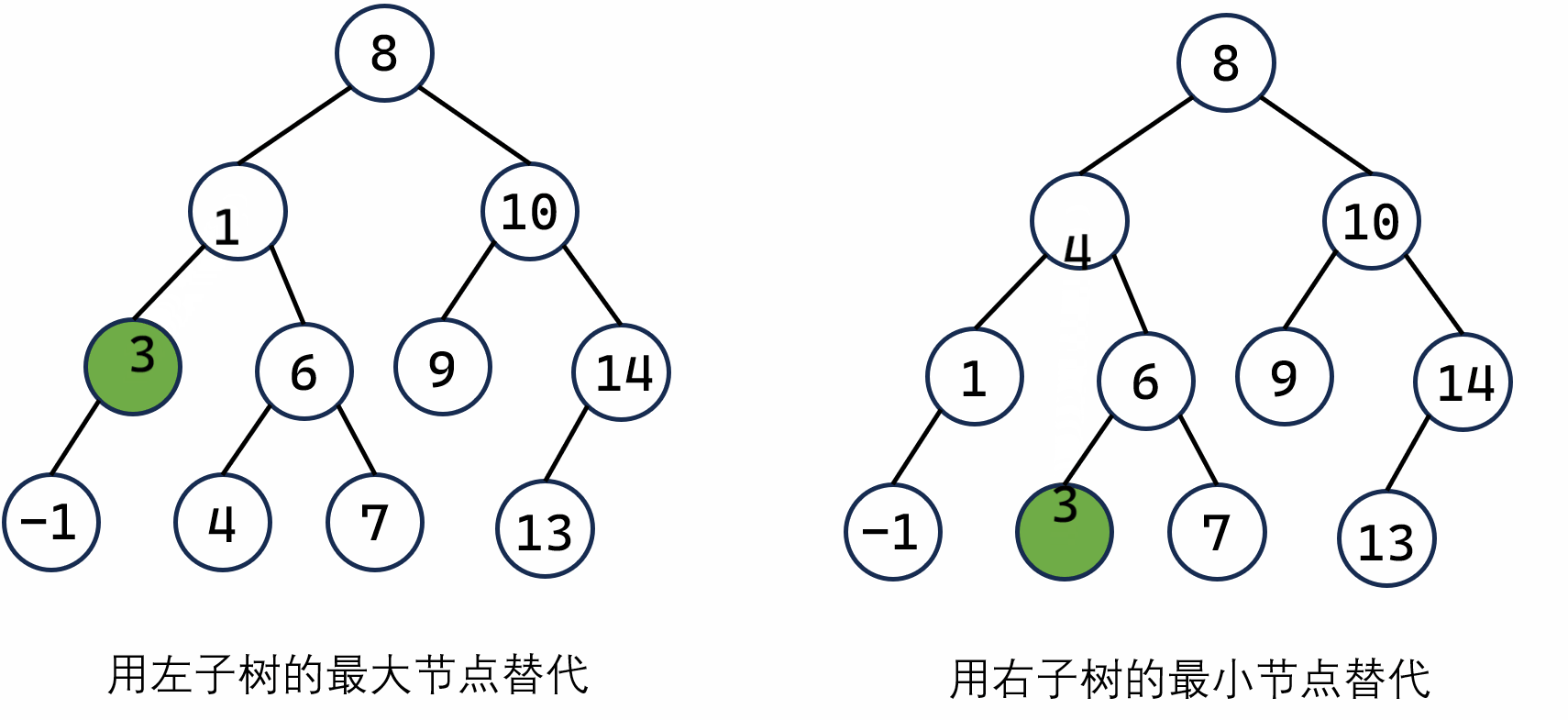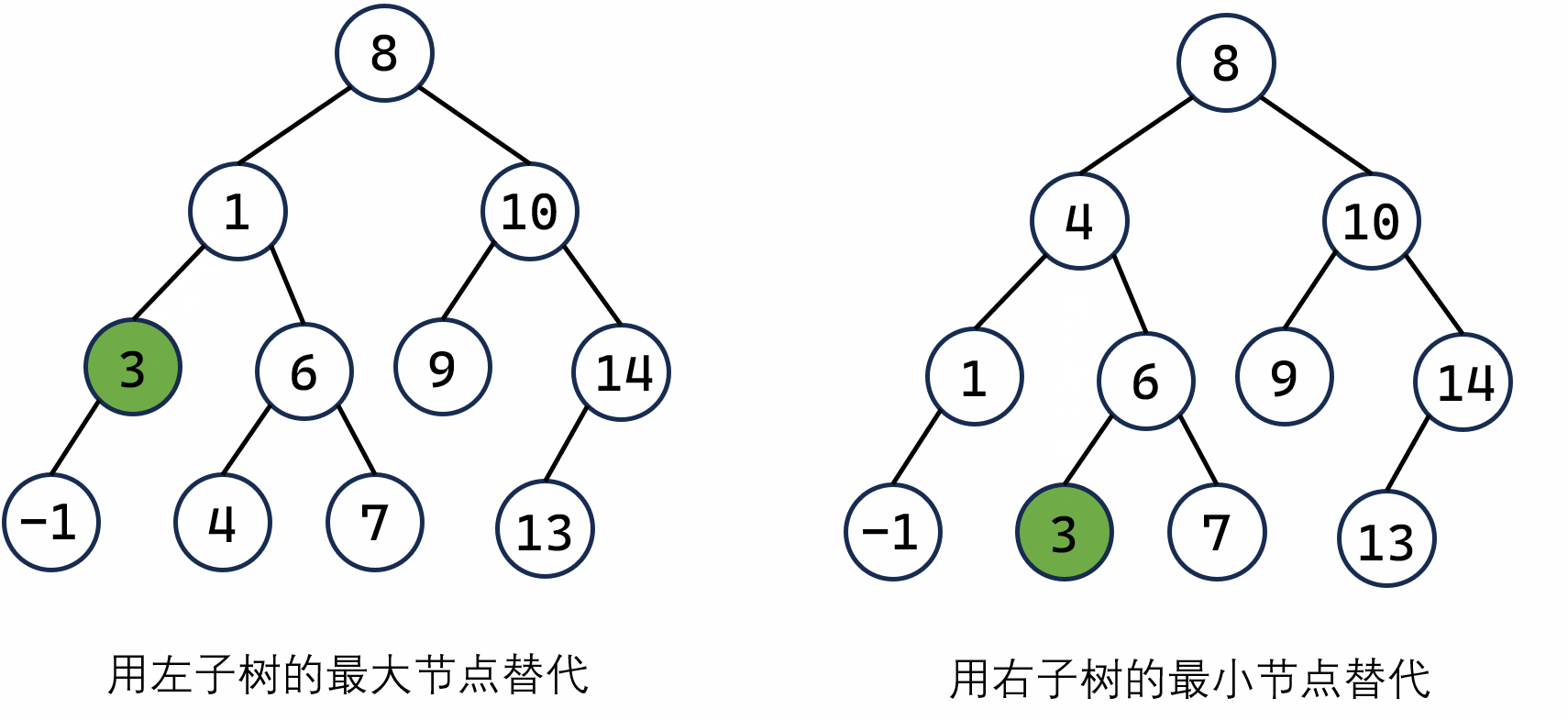
选择哪一个节点来替代待删除的节点呢?选择的依据就是,替代之后的树应满足二叉搜索树嘛!因此就会有两种选择的方式
例如:如上图,我们要删除 3 这个节点,可以选择左子树中最大的节点 1 来代替 3,或者选择右子树中最小的节点 4 来代替 3。这两种选法均可使得删除后的二叉树满足二叉搜索树的性质。
替换之后呢?要删除的节点的特性要么满足情况 1,要么满足情况 2。就很好办啦!
怎么找到二叉搜索树中的最大节点与最小节点呢?
- 二叉搜索树的最大节点位于整棵树的最右侧。
- 二叉搜索树的最小节点位于整棵树的最左侧。
其实经过仔细的观察,我们发现第一种情况和第二种情况是可以合并的!第一种情况是删除后父节点指针置空;第二种情况是删除后,父节点指向不为空的那个节点!
那么合并之后就是:如果待删除的节点的左孩子为空,那么令父节点指向右孩子就可以啦,否则,令父节点指向左孩子。或者如果待删除的节点的右孩子为空,那么令父节点指向左孩子,否者指向右孩子。
一定要看代码中的注释哦!还有一部分的细节在注释里面提到了。
bool erase(const K& key)
{
Node* prev = nullptr;
Node* cur = _root;
//找到要被删除的那个节点
while(cur)
{
if(key > cur->_key)
{
prev = cur;
cur = cur->_right;
}
else if(key < cur->_key)
{
prev = cur;
cur = cur->_left;
}
else //找到了那个要被删除的节点
{
//左子树为空,链接右子树
if(cur->_left == nullptr)
{
//这里是删除根节点的特殊情况
if(cur == _root)
_root = cur->_right;
else
{
//确定删除的节点位于其父节点的哪个位置
if(prev->_right == cur)
prev->_right = cur->_right;
else
prev->_left = cur->_right;
}
}
else if(cur->_right == nullptr) //右子树为空链接左子树
{
//处理删除根节点的特殊情况
if(cur == _root)
_root = cur->_left;
else
{
//确定删除的节点位于其父节点的哪个位置
if(prev->_right == cur)
prev->_right = cur->_left;
else
prev->_left = cur->_left;
}
}
else
{
//找到左子树中较大的那个节点,作为替换的节点
Node* leftMax = cur->_left;
Node* parent = cur;
while(leftMax->_right)
{
parent = leftMax;
leftMax = leftMax->_right;
}
//交换
swap(leftMax->_key, cur->_key);
//处理特殊情况,左子树的最大节点不一定是其父节点的右孩子
//当删除的节点的左孩子就是左子树的最大值,这就是那个特殊情况
if(parent->_left == leftMax)
{
parent->_left = leftMax->_left;
}
else
{
parent->_right = leftMax->_left;
}
cur = leftMax;
}
//删除节点
delete cur;
return true;
}
}
return false;
}