力扣题库-T707-奇偶链表-解析(Python)
题目
给定单链表的头节点
head,将所有索引为奇数的节点和索引为偶数的节点分别组合在一起,然后返回重新排序的列表。第一个节点的【索引】被认为是 奇数 , 第二个节点的索引为 偶数 ,以此类推。
请注意,偶数组和奇数组内部的相对顺序应该与输入时保持一致。
你必须在 【
O(1)的额外空间复杂度】和【O(n)的时间复杂度】下解决这个问题。
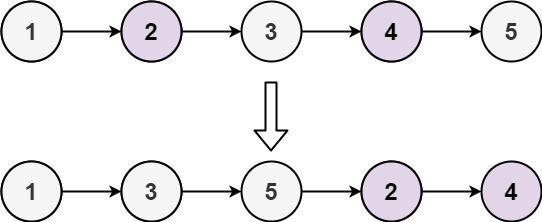
示例 1:
输入: head = [1,2,3,4,5] 输出: [1,3,5,2,4]
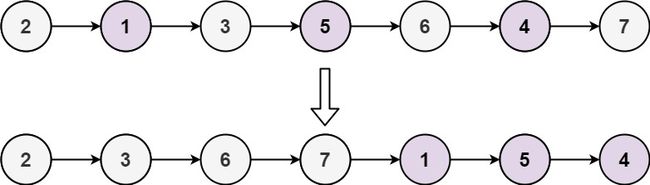
示例 2:
输入: head = [2,1,3,5,6,4,7] 输出: [2,3,6,7,1,5,4]
提示:
n ==链表中的节点数0 <= n <= 104-106 <= Node.val <= 106
题解
朴素算法
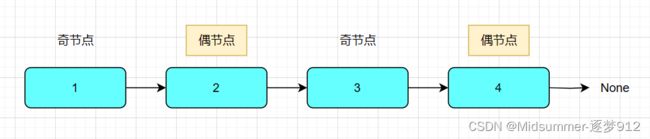
按照题目要求,索引,即【下标】(为了方便,此处所提的下标从1开始)为奇数的节点则认定其为【奇节点】,下标为偶数则认定其为【偶节点】。
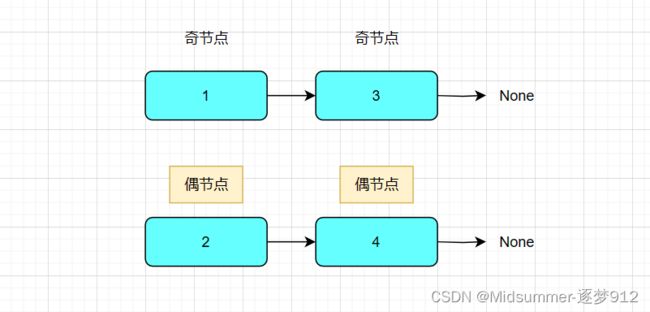
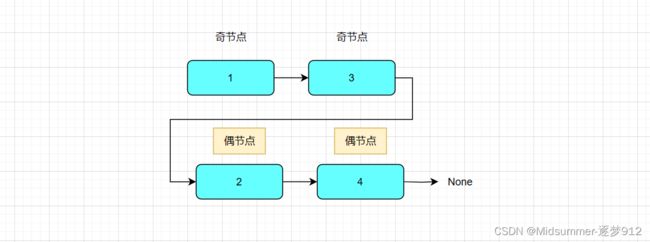
如此一来,我们按照最朴素的想法,可以将【奇节点】和【偶节点】分别从原来的链表中剥离出来,按照原始输入顺序,形成两个独立的链表。
最后,将两个独立链表中的【奇节点链表】的尾部连接到【偶节点链表】的第一个节点,这样,就完成了,奇偶链表的重排列。
图解完毕,我相信看图,你已经完全理解这种简单的方法了,接下来我们来实现这种傻瓜算法。
整体代码
# Definition for singly-linked list.
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
class Solution:
def oddEvenList(self, head: Optional[ListNode]) -> Optional[ListNode]:
odd = p1 = ListNode() #奇索引表【头节点】
even = p2 = ListNode() #偶索引表【头节点】
p1.next = p2.next = None #先让头节点都指向None
cur = head #head指向的就是第一个数据节点
count=1 #表示索引号,控制奇偶节点剥离
while cur:
temp=cur.next #temp是临时保存cur下一个节点的,否则会丢失后续节点
if count % 2 == 0: #分析索引的奇偶性,整个if语句实现节点剥离和插入到新表
cur.next = p1.next
p1.next = cur
p1 = cur
else:
cur.next = p2.next
p2.next = cur
p2 = cur
cur = temp #cur移动到后续未剥离的节点序列的第一个节点
count+=1 #每处理完一个,cur已经移动到下一个节点了,则索引+1
p2.next = odd.next #将【奇索引表】的尾巴和【偶索引表】的第一个节点连接
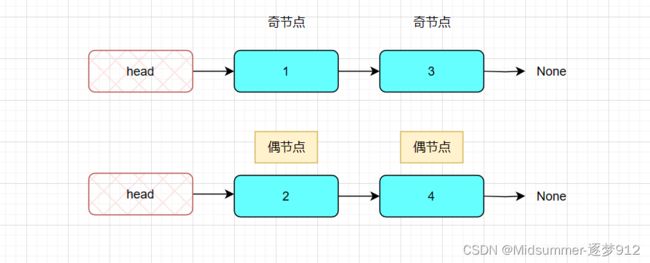
return even.next #返回重新排列后的链表的第一个数据节点其实代码的实现,和我上面的解析还有一点出入,那就是我在剥离奇偶节点后形成新的两个独立链表都是带头节点的,如下图:
之所以这样做,其实是为了方便一开始我的节点插入,由于一开始head.next为空,保证了后面我每次插入节点,通过【cur.next=p1/p2.next】都可以使cur直接指向None,这样就减少了在代码中多加一条指向None的语句。
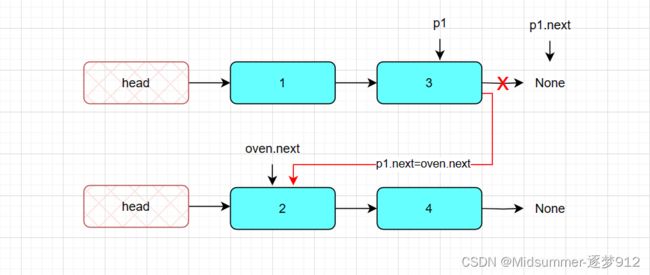
最后,由于p1会指向odd的末梢节点,p2会指向oven的末梢节点,则通过【p1.next=oven.next】就可以将两个链表合并!
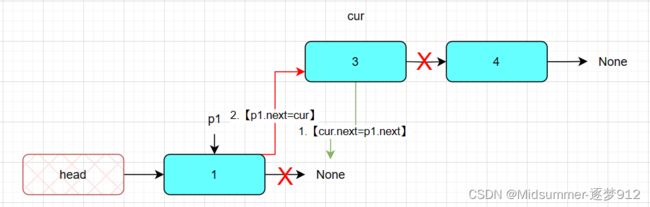
代码中间部分,有一个 【temp=cur.next 】,使因为,下面的插入算法会丢失后面的节点,如下图所示,第一步就是掐掉了cur和后面节点的连线。
第二步,【p1.next=cur】至此cur从原链表中剥离完毕,也插入完毕,如下图所示
第三步,为了每一次节点都是按照正序插入到新表中,这要求p1始终指向尾巴节点,如此而言,就引出了【p1=cur】,其实更标准的是【p1=p1.next】,但是在cur更新之前,p1.next和cur是指向同一个节点的因此可以混用。
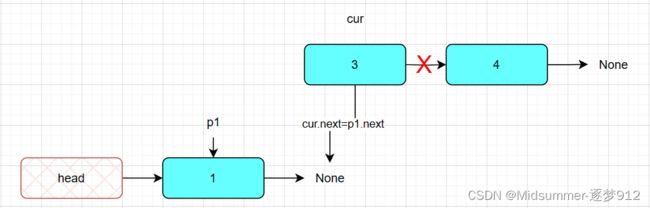
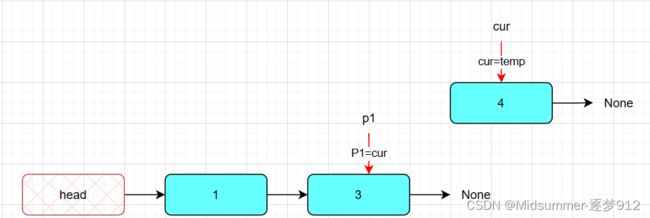
最后,由于,cur仍然指向节点3,如果不加以操作,将丢失节点4,但是好在我们最开始用【temp=cur.next】,将节点4保存了下来,因此最后通过【cur=temp】可以重新让cur指向4。
最后两部操作如图:
优化算法(跳跃连接法)
我们常常需要想,除了朴素算法是否自己能想出更加优化的算法呢?是的,本题,还有一种广为流传的优化算法,我们现在开始来介绍思想。
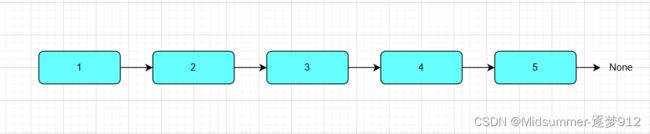
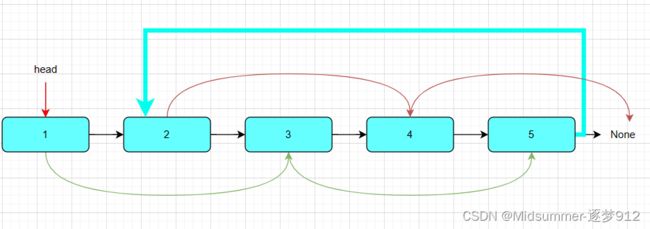
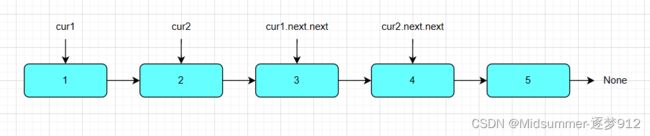
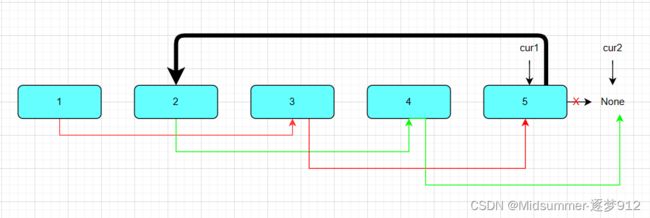
现有如上链表,需要将如上链表转换成奇偶链表。 现在我直接告诉你,本算法将要实现如下图连接,所有操作都在原链表上进行操作。
要实现以上连接啊,咱们就来看看各节点之间的关系,一下是关系图
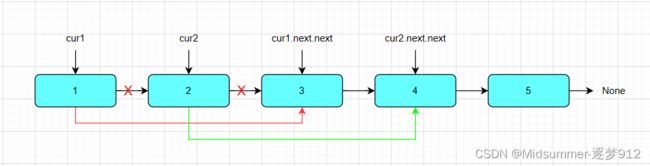
好的,那么此时相信,你已经了解到怎么将1和3连接起来,2和4连接起来了,通过【cur1.next=cur1.next.next】和【cur2.next=cur2.next.next】即可,如下图:
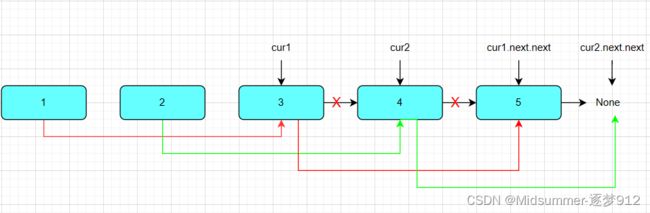
不失一般性,要将3和5连接,4和None连接,是不是同样的操作,只是此时需要移动cur指针,由于cur所在节点已经被先前的操作重定向,那么要将cur1移动到3的位置只需要【cur1=cur1.next】即可 ,cur2同理,最终实现,下图所示连接图:
同样,继续移动cur,得到下图
我们发现,cur2此时为None了,如果继续做先前的连接操作,势必会造成严重的后果。因此此时需要停止先前重复的【移动】和【连接】操作,因此cur2为None是以上循环操作停止的一个条件。
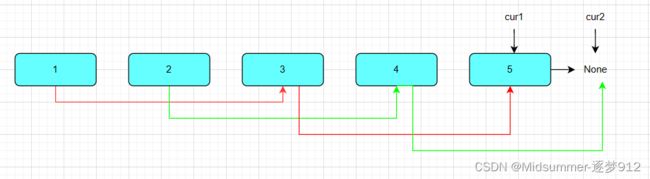
最后,我们都可以看出,其实奇偶链表已经分明了,此时只需要将他们连接起来即可,一条语句【cur1.next=even】,别忘记了oven是指向2的哈哈,那么就有下图咯
可以看出所有连接关系都已经完整了,只需要返回节点1即可。
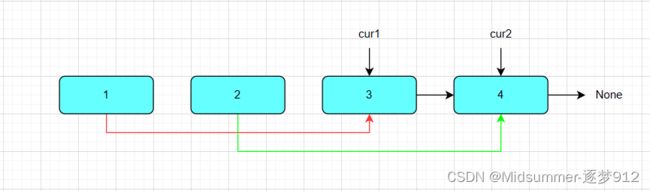
可是还没完,还有一种情况,节点个数是偶数个的情况。
中间操作和第一种情况是一样的,这里不再赘述,只是结束操作的情况稍稍不同,如下图,虽然此时cur1还可以连接到None,但是cur2.next就为None了,意味着cur2.next.next不存在,不能继续往下连接和移动了,此时只需要连接奇偶表即可。
因此,【cur2.next=None】也是一个连接和移动操作结束记号;如果你还没有忘记,那么前面也有一个结束条件,+上这个就有2个啦!
至此我们全部分析完毕整个算法实现过程,现在 来看看代码吧,我码字好累了。
整体代码
# Definition for singly-linked list.
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
class Solution:
def oddEvenList(self, head: Optional[ListNode]) -> Optional[ListNode]:
if not head:
return
odd = head #奇索引表-第一个节点
even = head.next #偶索引表-第一个节点
cur1,cur2=odd,even #odd和even作为表头不能动,为了方便操作再取两个可以移动的指向
while cur2 and cur2.next:
cur1.next=cur1.next.next #跨越下一个偶节点,直接连接下一个奇节点
cur2.next=cur2.next.next #跨越下一个奇节点,直接连接下一个偶节点
cur1=cur1.next #移动到新奇表的下一个位置
cur2=cur2.next #移动到新偶表的下一个位置
cur1.next=even #将奇表尾和偶表头连接起来
return odd #返回重新排列后的链表的第一个数据节点那么整个算法就介绍完毕了,如果有不懂或者本题解有误之处,敬请大家之处。
小结
题解到这里就结束咯,可能有的人会喷,这么简单的东西还长篇大论。但是我想说的是,不管你有多厉害,你也是从基础开始的,每个人基础不同,理解能力不同,能力强不一定能把东西讲明白,既然是做分享的,那就要做好,不误人子弟。
现在,博客很严重的现象,相信大家也都看到了,抄袭的文章一大堆,质量也不咋地,搞得国内类似的社区乌烟瘴气。
好的东西要学习,多看看国外的博客文章是个什么样的体验感。
还有也没有必要看不起朴素算法,有的时候,某人搞个让人看不懂的代码,标个标题【3行实现】,实际上既难读,效果还不一定有朴素算法好。
最后,我想跟大家说1句:一定要做一个细心的人。
因为粗心,我打错了大小写,bug找了我不知道多长时间。另外,题目没看清,以为是判断节点值的奇偶,其实是索引的奇偶,最终导致运行结果不对,想了许久
泡杯龙井提神吧!深夜了!