算法通关村 —— 滑动窗口经典问题

目录

滑动窗口经典问题

1. 最长子串专题

1.1 无重复字符的最长子串

1.2 至多包含两个不同字符的最长子串

1.3 至多包含K个不同字符的最长子串

2 长度最小的子数组

3 盛水最多的容器

4 寻找子串异位词

4.1 字符串的排列

4.2 找到字符串中所有字母异位

---

滑动窗口经典问题

前面我们已经了解了滑动窗口的基本思想，今天让我们一起来完成有关滑动窗口的经典算法题。

1. 最长子串专题

这是一道高频算法题: 无重复字符的最长子串。具体要求是给定一个字符串 s，请你找出其中不含有重复字符的最长子串的长度。例如，输入:s ="abcabcbb"，则输出3，因为无重复字符的最长子串是"abc"，所以其长度为3。

如果再变一下要求，至多包含两个不同字符的最长子串，或者至多包含 K 个不同字符的最长子串，该怎么做呢……这些都可以用滑动窗口来解决。而且本质上都是一个解题模板。

1.1 无重复字符的最长子串

给定一个字符串 s ，请你找出其中不含有重复字符的最长子串的长度。例如:

输入: s ="abcabcbb"
输出: 3
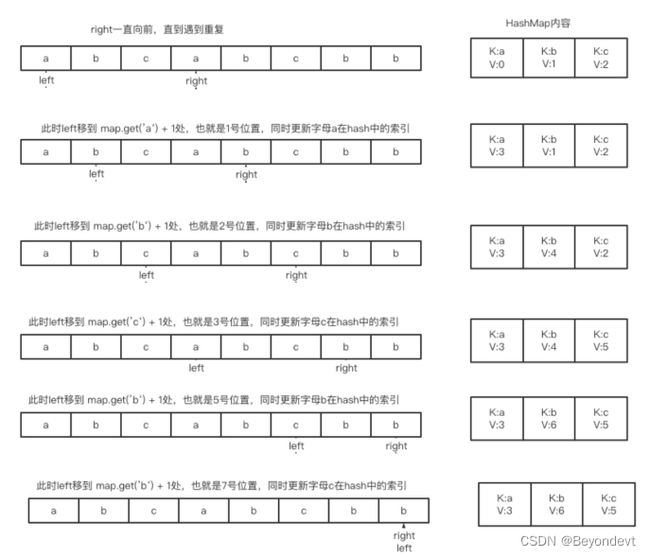
解释:因为无重复字符的最长子串是 “abc"，所以其长度为 3。

要找最长子串，必然要知道无重复字符串的首和尾，再从中确定最长的那个，因此至少要两个指针，这就想到了滑动窗口思想。这里介绍一种经典的使用Map的思路。我们定义一个K-V形式的map，key表示的是当前正在访问的字符串，value是其下标索引值。我们每访问一个新元素，都将其下标更新成对应的索引值。具体过程如下图：

如果字符已经出现过，例如abcabc，当第二次遇到a时，就更新left成为第一个b所在的位置，也就是map.get('a') + 1=1，用序列来表示就是map.get(s.charAt(i)) + 1。其他情况依次类推。

特殊情况：例如abba，当第二次访问b时，left=map.get('b')+1=2。
然后继续访问第二个a，此时left=map.get('a') + 1=1，left后退了，显然不对。应该让left在2的基础上继续向前，只需和原来的对比一下，将最大的加1就可以了，也就是:
left = Math.max(left,map.get(s.charAt(i)) + 1), 即要么重复的元素在left之前则不需要移动，要么在left之后则移动到重复元素的所在位置+1.

完整代码如下：

class Solution {
    public int lengthOfLongestSubstring(String s) {
        if(s.length() == 0) return 0;
        // 存储各字母及其对应索引的哈希表
        HashMap map = new HashMap<>();
        int left = 0; // 滑动窗口左指针
        int max = 0; // 存储无重复字符串最大值
        for(int right =  0; right < s.length(); right++){
            // 若当前字符已在map中存在，则更新滑动窗口左指针位置
            if(map.containsKey(s.charAt(right))){
                left = Math.max(left, map.get(s.charAt(right)) + 1); // 更新left位置
            }
            // 更新map字符及索引
            map.put(s.charAt(right), right);
            max = Math.max(max, right - left + 1); // 更新当前无重复字符串最大长度
        }
        return max;
    }
}

1.2 至多包含两个不同字符的最长子串

现在比上一道题多了一个限制。给定一个字符串s, 找出至多包含两个不同字符串的最长子串t, 并返回该子串的长度。例如：

输入："eceba"
输出：3
解释：t 是 "ece", 长度为3

该题仍然使用left和right来锁定一个窗口，然后一边移动指针一边分析，也就是“滑动窗口思想”

以序列 "aabbccccd" 来看：

所以最后可看至多包含两个不同字符的最长子串长度为5.

下面我们来解决两个问题：

1. 如何判断只有两个元素：和上一道题一样，我们还是用HashMap, 每一时刻 HashMap 包含不超过3个元素。

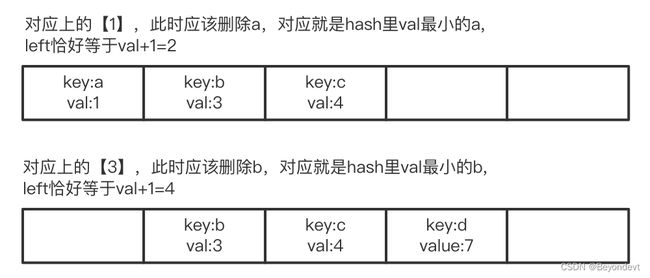
2. 移除的时候移除谁，移除后left是什么：这就需要我们设计一HashMap的Key-Value含义了，在这里我们把字符都当作键，该字符在窗口最右边的位置作为值，因为我们要移除值肯定是移除窗口左边的字符，也就是每个字符在map中对应的value的最小值(注意：这里value为字符在窗口最右边的值，这样才能完全地把该字符移除掉），移除完后，left就是该移除字符对应value+1,如下图：

public static int lengthOfLongestSubstringTwoDistinct(String s) {
    if (s.length() < 3) {
        return s.length();
    }
    int left = 0, right = 0;
    // 存储遍历到的字符和对应在窗口中的最右索引
    HashMap hashmap = new HashMap<>();
    int maxLen = 2; // 存储最大长度
    while (right < s.length()) {
        if (hashmap.size() < 3)
            hashmap.put(s.charAt(right), right++);
        // 如果字符数量达到了3个则要删掉最左边的字符
        if (hashmap.size() == 3) {
            // 获取最左侧要删除的位置
            int del_idx = Collections.min(hashmap.values());
            hashmap.remove(s.charAt(del_idx));
            // 窗口left的新位置
            left = del_idx + 1;
        }
        // 更新最长子串长度
        maxLen = Math.max(maxLen, right - left);
    }
    return maxLen;
}

1.3 至多包含K个不同字符的最长子串

在第二道题的基础上，我们将限制要求扩大范围。

给定一个字符串s， 找出至多包含 k 个不同字符的最长字串T。如下：

输入：s = "eceba", k = 2
输出：3
解释：T为至多包含k = 2个字符的最长子串"ece", 所以长度为3.

该题只是把2换成k让我们自己来指定而已，那本质上是不是一模一样的呢？没错，所以我们只要把2换成k即可, 如果超过了长度2现在就是k+1了。具体实现代码如下：

public static int lengthOfLongestSubstringKDistinct(String s, int k) {
    if (s.length() < k + 1) {
        return s.length();
    }
    int left = 0, right = 0;
    // 存储遍历到的字符和对应在窗口中的最右索引
    HashMap hashmap = new HashMap<>();
    int maxLen = k; // 存储最大长度
    while (right < s.length()) {
        if (hashmap.size() < k + 1)
            hashmap.put(s.charAt(right), right++);
        // 如果字符数量达到了3个则要删掉最左边的字符
        if (hashmap.size() == k + 1) {
            // 获取最左侧要删除的位置
            int del_idx = Collections.min(hashmap.values());
            hashmap.remove(s.charAt(del_idx));
            // 窗口left的新位置
            left = del_idx + 1;
        }
        // 更新最长子串长度
        maxLen = Math.max(maxLen, right - left);
    }
    return maxLen;
}

2 长度最小的子数组

给定一个含有 n 个正整数的数组和一个正整数 target。找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl,numsl + 1,..., numsr - 1,numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0。

输入: target = 7，nums = [2,3,1,2,4,3]
输出: 2
解释: 子数组 [4,3] 是该条件下的长度最小的子数组。

本题同样涉及到区间中的处理，所以依然使用双指针来解决，也可以视为队列法

基本思路是先让元素不断入队，当入队元素和大于target时就记录一下此时队列的容量，然后开始出队，直到小于target则再继续入队。
如果出现等于target的情况，则记录一下此时队列的大小，之后继续先入队再出队。每当出现元素之和等于target时我们就保留容量最小的那个。实现代码如下:

public static int minSubArrayLen(int target, int[] nums) {
    int left = 0, right = 0, sum = 0, min = Integer.MAX_VALUE;
    while (right < nums.length) {
        // 数组元素不断入队直到大于等于target
        sum += nums[right++];
        while (sum >= target) {
            // 更新此时最小长度
            min = Math.min(min, right - left);
            // 移除最左边元素，然后left++
            sum -= nums[left++];
        }
    }
    return min == Integer.MAX_VALUE ? 0 : min;
}

3 盛水最多的容器

给定一个长度为 n 的整数数组 height。有 n 条垂线，第i条线的两个端点是(i, 0) 和(i, height[i])。找出其中的两条线，使得它们与x轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。如下图所展示：

输入: [1,8,6,2,5,4,8,3,7]
输出: 49
解释:图中垂直线代表输入数组[1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水
的最大值为 7 * ( 9 - 2) = 49

本题看似复杂，但其实简单的很。涉及到区间内的处理，还是设两指针i，j，指向的水槽板高度分别为 h[i] ,hlj] ，此状态下水槽面积为S(j)。由于可容纳水的高度由两板中的 短板 决定，底边长为   j - i, 因此可得如下面积公式:          s(j) = min(h[ i ] ,h[ j ]) x (j - i)

那我们寻找最大面积时要移动哪个板块呢，下面我们来分析一下：

在每个状态下，无论长板或短板向中间收窄一格，都会导致水槽底边宽度-1 变短:

⚪ 若向内移动短板，水槽的短板min(h[i] ,h[j]) 可能变大，因此下个水槽的面积可能增大
⚪ 若向内移动长板，水槽的短板min(h,hli) 不变或变小，因此下个水槽的面积一定变小

因此，只要初始化双指针分列水槽左右两端，循环每轮将短板向内移动一格，并更新面积最大值，直到两指针相遇时跳出;即可获得最大面积。

public static int maxArea(int[] height) {
    int i = 0, j = height.length - 1, res = 0;
    while (i < j) {
        // 每次更新最大值后移动短板所在指针索引
        res = height[i] < height[j] ?
                Math.max(res, (j - i) * height[i++]) :
                Math.max(res, (j - i) * height[j--]);
    }
    return res;
}

4 寻找子串异位词

异位词： 如果两个字符串仅仅是字幕出现位置不一样，则称两者相互为对方的一个排列，或异位词。 判断两个字符串是否为排列，也是字符串的一个基本算法。

4.1 字符串的排列

给你两个字符串s1和s2，写一个函数来判断 s2是否包含 s1的排列。如果是，返回 true ;否则，返回 false 。换句话说，s1 的排列之一是s2 的子串 。其中s1和s2都只包含小写字母。
 

输入: s1 ="ab" s2 ="eidbaooo"
输出: true
解释: s2 包含 s1 的排列之一 ("ba")

本题因为字符串s1的异位词长度一定是和s2字符串的长度一样的，所以不需要用高代价的排序

所谓的异位词不过两点: 字母类型一样，每个字母出现的个数也是一样的。题目说s1和s2都仅限小写字母，因此我们可以创建一个大小为26的数组，每个位置就存储从a到z的个数，为了方便操作，索引我们使用 index=s1.charAt(i) - 'a' 来表示，这是处理字符串的常用技巧                          此时窗口的right向右移动就是执行:charArray2[s2.charAt(right) - 'a']++;而left向右移动就是执行 int left = right - SLen1; charArray2[s2.charAt(left) - 'a']--; 

具体实现代码如下：

public class CheckInclusion {
    public static boolean checkInclusion(String s1, String s2) {
        int sLen1 = s1.length(), sLen2 = s2.length();
        if (sLen1 > sLen2) {
            return false;
        }
        int[] charArray1 = new int[26]; // 存放s1 字母出现次数的数组
        int[] charArray2 = new int[26]; // 存放s2 字母出现次数的数组
        //先读最前面的一段（与s1等长）来判断。
        for (int i = 0; i < sLen1; ++i) {
            ++charArray1[s1.charAt(i) - 'a'];
            ++charArray2[s2.charAt(i) - 'a'];
        }
        // 判断此时两存储数组是否相同
        if (Arrays.equals(charArray1, charArray2)) {
            return true;
        }
        // s2右指针继续向右遍历并记录到数组里，去除左指针产生的数据
        for (int right = sLen1; right < sLen2; ++right) {
            // 继续向右遍历并记录到数组里
            charArray2[s2.charAt(right) - 'a']++;
            int left = right - sLen1; // 左指针索引
            // 左指针索引在数组中的出现次数减一
            charArray2[s2.charAt(left) - 'a']--;
            // 再次判断是否相同
            if (Arrays.equals(charArray1, charArray2)) {
                return true;
            }
        }
        return false;
    }
    // 测试
    public static void main(String[] args) {
        String s1 = "ab", s2 = "eidbaooo";
        System.out.println(checkInclusion(s1, s2));
    }

}

4.2 找到字符串中所有字母异位

找到字符串中所有字母异位词，给定两个字符串 s 和 p，找到s 中所有 p 的 异位词 的子串，返回这些子串的起始索引。不考虑答案输出的顺序。注意s和p仅包含小写字母。

输入: s ="cbaebabacd"，p ="abc"
输出: [0,6]
解释:
起始索引等于 0 的子串是“cba"，它是“abc”的异位词。
起始索引等于 6 的子串是“bac"，它是“abc”的异位词。

本题的思路和实现与上面几乎一模一样，唯一不同的是需要用一个List，如果出现异位词，还要记录其开始位置，那直接将其add到list中就可以了。完整代码如下：

public class FindAnagrams {
    public static List findAnagrams(String s, String p) {
        int sLen = s.length(), pLen = p.length();
        if (sLen < pLen) {
            return new ArrayList();
        }
        List ans = new ArrayList();
        int[] sCount = new int[26];
        int[] pCount = new int[26];
        //先分别初始化两个数组
        for (int i = 0; i < pLen; i++) {
            sCount[s.charAt(i) - 'a']++;
            pCount[p.charAt(i) - 'a']++;
        }
        if (Arrays.equals(sCount, pCount)) {
            ans.add(0);
        }

        for (int left = 0; left < sLen - pLen; left++) {
            sCount[s.charAt(left) - 'a']--;
            int right = left + pLen;
            sCount[s.charAt(right) - 'a']++;

            if (Arrays.equals(sCount, pCount)) {
                //上面left多减了一次，所以需要+1
                ans.add(left + 1);
            }
        }
        return ans;
    }
    // 测试
    public static void main(String[] args) {
        String s = "cbaebabacd", p = "abc";
        System.out.println(findAnagrams(s, p));

    }

}