算法题:99.恢复二叉搜索树
(为不影响大家的观感,完整题目附在了最后)
二叉搜索树的定义
二叉搜索树(BST,Binary Search Tree),也称二叉排序树或二叉查找树。
二叉搜索树:一棵二叉树,可以为空;如果不为空,满足以下性质:
- 非空左子树的所有键值小于其根结点的键值。
- 非空右子树的所有键值大于其根结点的键值。
- 左、右子树都是二叉搜索树。
恢复二叉搜索树的解法分析
由二叉搜索树的定义可推知:二叉搜索树的中序遍历结果一定是严格由小到大排序的。由于“恢复二叉搜索树”的题目中指出“恰好两个节点的值被错误地交换”,那么我们只要找出破坏了这个顺序的两个节点,交换其节点值就可以了。
阅读本篇内容时,可结合本人在另一个博客中详细分析的 Morris 中序遍历方法:
算法:实现中序遍历(3种方法:递归、迭代、Morris)-CSDN博客
本题最优解法是采用 Morris 中序遍历方法,也就是题目进阶要求里的使用 O(1) 空间的解决方案,本人之前掌握的 Morris 中序遍历方法,在遍历的过程中是会改变树的结构的,会影响到层序遍历的结果,而本题要求的输出是层序遍历的,因此改变树的结构不可行。为此,我又学习了另一种最终不会改变树的结构的 Morris 中序遍历方法,我在这里重新贴一下代码,具体的原理分析还请看我上面分享的博文,那里面写的很详细,步骤都有画出来。
class Solution(object):
def inorderTraversal(self, root):
res = []
while root:
if root.left:
temp = root.left
while temp.right and temp.right != root:
temp = temp.right
if not temp.right:
temp.right = root
root = root.left
else: # temp.right == root 的情况
res.append(root.val)
temp.right = None
root = root.right
else:
res.append(root.val)
root = root.right
return res恢复二叉搜索树的完整代码
接下来,只要在其中加一些判断语句,找出中序遍历后不服从由小到大顺序的两个结点进行值的交换即可,完整测试代码如下:(提交时只需要提交recoverTree()函数代码,层序遍历的输出是力扣自动帮忙完成的)
# Definition for a binary tree node.
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def recoverTree(self, root):
x, y = None, None # 设置两个变量,代表被错误交换的两个节点
pre = None
while root:
if root.left:
tmp = root.left
while tmp.right and tmp.right != root:
tmp = tmp.right
if tmp.right is None:
tmp.right = root
root = root.left
else: # temp.right == root 的情况
if pre and pre.val > root.val: # 新加入的判断语句
# 假设最先遇到的两个不符合顺序的结点就是最终要找的两个节点
if not x:
x = pre
y = root
else: # 如果后面又遇到了不符合顺序的结点,则 y 需要变
y = root
pre = root
tmp.right = None
root = root.right
else:
if pre and pre.val > root.val: # 新加入的判断语句
if not x:
x = pre
y = root
else:
y = root
pre = root
root = root.right
if x and y:
x.val = x.val ^ y.val
y.val = x.val ^ y.val
x.val = x.val ^ y.val
def levelOrder(self, root): # 层序排列
if not root:
return []
res = []
queue = [root]
while len(queue) > 0:
size = len(queue)
temp = []
for i in range(size): # 确保了每层的结点值在同一个数组内
# 通过append、pop(0)的方法用数组构造了一个先进先出的列表
node = queue.pop(0)
temp.append(node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
res.append(temp)
return res
if __name__ == '__main__':
# 创建一个二叉树
tree = TreeNode(3)
tree.left = TreeNode(1)
tree.right = TreeNode(4)
tree.right.left = TreeNode(2)
# 执行中序遍历
sol = Solution()
sol.recoverTree(tree)
print(sol.levelOrder(tree)) # [[2], [1, 4], [3]]
如果对这里的层序遍历的代码感兴趣,可以看我的这篇博文:
算法题:二叉树的层序遍历-CSDN博客
恢复二叉搜索树的完整题目
给你二叉搜索树的根节点 root ,该树中的 恰好 两个节点的值被错误地交换。请在不改变其结构的情况下,恢复这棵树 。
示例 1:
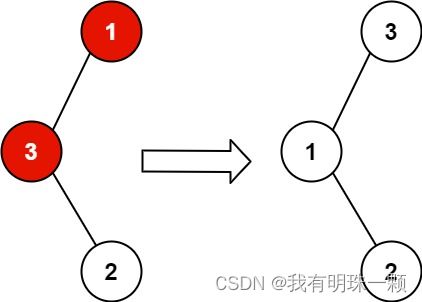
输入:root = [1,3,null,null,2] 输出:[3,1,null,null,2] 解释:3 不能是 1 的左孩子,因为 3 > 1 。交换 1 和 3 使二叉搜索树有效。
示例 2:
输入:root = [3,1,4,null,null,2] 输出:[2,1,4,null,null,3] 解释:2 不能在 3 的右子树中,因为 2 < 3 。交换 2 和 3 使二叉搜索树有效。
提示:
- 树上节点的数目在范围
[2, 1000]内 -2^31 <= Node.val <= 2^31 - 1
进阶:使用 O(n) 空间复杂度的解法很容易实现。你能想出一个只使用 O(1) 空间的解决方案吗?