用A*算法解决15数码问题(8数码问题)c++
目录
- 十五数码问题
- 算法
-
- 启发函数
- A*算法步骤
- 结点的表示
- 数据结构
-
- 目标状态St的存储
- Open表和Close表的存储
- A*算法程序
- 结果讨论
给出了一种基于散列表和红黑树存储open表和close表的A*算法程序,提升了速度。
十五数码问题
完整代码可参见 github 或 gitee
十五数码问题是人工智能中状态搜索中的经典问题,其中,该问题描述为:在4×4的棋盘,摆有十五个棋子,每个棋子上标有1至15的某一数字,不同棋子上标的数字不相同。棋盘上还有一个空格,与空格相邻的棋子可以移到空格中。要求解决的问题是:给出一个初始状态和一个目标状态,找出一种从初始转变成目标状态的移动棋子步数最少的移动步骤。
这是一个典型的图搜索问题,但是该问题并不需要正在建立图数据结构来进行求解,而是将图的搜索方法抽象,运用到该问题上。
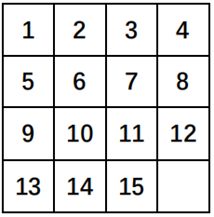
初始状态为
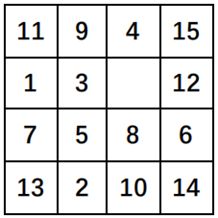
通常,在程序中以0代替空位。
算法
启发函数
G ( S ) = D i s ( S ) + D e p t h ( S ) ∗ a l p h a G(S)=Dis(S)+Depth(S)*alpha G(S)=Dis(S)+Depth(S)∗alpha
其中Dis(S)表示该数字到目标数字的曼哈顿距离,Depth(S)表示结点的深度(初始结点深度为0)。系数alpha用于控制距离和深度信息两者的比重。当alpha较小时,则启发函数更体现结点的深度信息;当alpha较大时,启发函数体现更多的深度信息。
A*算法步骤
给定初始节点S0, 目标节点St, 深度信息权重alpha
Push(open, S0) //将S0放入Open表
while Open非空 && 循环次数<1000000:
Sp = Min(open) //寻找open表中估价函数最小的
Pop(Open, Sp) //从Open表中删除Sp
for d in [上,下,左,右]: //对四个方向分别扩展
if Extendable(Sp, d): //判断节点是否可扩展
Sp’ = Extend(Sp, d) //扩展出的新结点
G(Sp’) = Dis(Sp’) + depth(Sp’) * alpha
if Find(Open, Sp’):
比较两个节点启发函数大小,若Sp’较小,则用Sp'替换较大的结点
else if Find(Close, Sp’):
比较两个节点启发函数大小,若Sp’较小Push(Open, Sp’), 并从Close表中删除较大的节点
else:
Push(Open, Sp’)
end if
end if
end for
Push(Close, Sp)
end while
结点的表示
#define SIZE 4 //数组大小 SIZE*SIZE
typedef int table[SIZE][SIZE]; // to store the data
class State
{
public:
int zero_row; // position of zero
int zero_col;
double fvalue;
int depth; // the depth of state in the tree
double distance; // the sum of the distance of the num out of position
string str_num; // str of data, used for open/close map
State* father; // previous node
State(table, int);
~State();
int get_distance(unordered_map<int, pos>); // city block distance
double evaluate(unordered_map<int, pos>, double); // return fvalue = depth*alpha + distance
string get_str_num(); // data => string
State* extend(); // generate a new node
void move_up(); // move zero 扩展节点
void move_left();
void move_down();
void move_right();
void show_table(); // 打印棋盘
private:
table data;
};
数据结构
目标状态St的存储
为了更快地计算棋盘中每个数到目标位置的曼哈顿距离,用散列表std::unordered_map存储目标状态中每个数的位置,一个数对应一个位置(row, col)。
//用一个结构体存储一个数的位置
typedef struct
{
int row;
int col;
}pos;
unordered_map<int, pos> get_target_map(table target)
{
// write a table to a map
unordered_map<int, pos> target_map;
for (int i = 0; i < SIZE; ++i) {
for (int j = 0; j < SIZE; ++j) {
pos p{ i, j };
target_map.insert(pair<int, pos>(target[i][j], p));
}
}
return target_map;
}
Open表和Close表的存储
上边这一步的操作其实影响较小,在A*算法中真正耗费时间的主要是在open表和close表中搜索。
同样,采用散列表的方式存储open表和close表,判断该结点的状态是否存在。这里,我将每个结点的棋盘数字打平,并存储成字符串形式,作为散列表的Key. 如,目标状态应表示为
1-2-3-4-5-6-7-8-9-10-11-12-13-14-15-0
转换代码
string table2string(table a)
{
string s;
for (int i = 0; i < SIZE; ++i) {
for (int j = 0; j < SIZE; ++j)
s += to_string(a[i][j]) + "-";
}
return s;
}
这样就可以用unordered_map的方式存储open表和close表。
但散列表是无序的,为了能够在节点插入open表时就根据fvalue进行排序,使用红黑树std::set的结构再建立一个有序Open表,并自定义排序方式
struct cmp {
bool operator()(const State* a, const State* b) const
{
if (a->fvalue == b->fvalue)
return a < b;
return a->fvalue < b->fvalue;
}
};
set<State*, cmp> open_set;
A*算法程序
完整代码可参见https://github.com/sby9981/A_project
并以如下结构安放文件
A*算法程序
State* process(State* new_node, unordered_map<string, State*>& open_map, set<State*, cmp>& open_set,
unordered_map<string, State*>& close_map, const unordered_map<int, pos> target_map, double alpha)
/* 处理新结点,在open表和close表中搜寻新结点的状态是否存在
* new_node: 新生成的结点
* open_map: 存放全部节点字符串id的open表
* open_set: 节点按估价函数fvalue排序后的open表
* close_map: 存放全部节点字符串id的close表
* target_map: 最终目标棋盘状态的数字和位置信息
* alpha: 深度信息的权重fvalue = distance + depth * alpha;
* return final_node: 若找到解,返回解的节点,若未找到,返回空
*/
{
State* final_node = 0;
unordered_map<string, State*>::iterator it_open = open_map.find(new_node->str_num),
it_close = close_map.find(new_node->str_num);
if (it_open != open_map.end()) {
new_node->evaluate(target_map, alpha);
if (it_open->second->fvalue > new_node->fvalue) {
set<State*, cmp>::iterator it = open_set.find(it_open->second);
open_set.erase(it);
open_set.insert(new_node);
it_open->second = new_node;
}
}
else if (it_close != close_map.end()) {
new_node->evaluate(target_map, alpha);
if (it_close->second->fvalue > new_node->fvalue) {
open_map.insert(pair<string, State*>(new_node->str_num, new_node));
open_set.insert(new_node);
close_map.erase(it_close);
}
}
else {
new_node->evaluate(target_map, alpha);
if (new_node->distance == 0) {
final_node = new_node;
}
open_map.insert(pair<string, State*>(new_node->str_num, new_node));
open_set.insert(new_node);
}
return final_node;
}
deque<State*> A_solution(State* startnode, table target, double alpha)
/* A*算法主程序
* startnode: 初始状态的结点
* target: 最终目标棋盘状态的数字和位置信息
* return solution: 解的结点路径
*/
{
State* final_node = 0; // its data is target {1,2,3...15,0}
deque<State*> solution; // the node chain lead to final_node
set<State*, cmp> open_set; // it's sorted by fvalue
unordered_map<int, pos> target_map = get_target_map(target);
unordered_map<string, State*> open_map, close_map;
int node_num = 0; // the totle num of node <==> the step to the final solution
int loop_num = 0; // the loop num of while
clock_t start1, end1;
start1 = clock();
startnode->evaluate(target_map, alpha);
open_set.insert(startnode);
open_map.insert(pair<string, State*>(startnode->get_str_num(), startnode));
while (open_set.size() && loop_num < 1000000) {
State* node = *open_set.begin();
open_set.erase(open_set.begin());
unordered_map<string, State*>::iterator node_it = open_map.find(node->str_num);
open_map.erase(node_it);
if (loop_num++ % 1000 == 0)
cout << loop_num << ": " << node->fvalue << " "
<< node->distance<< " "<< node->depth << endl;
if (node->zero_row > 0) {
State* new_node = node->extend();
new_node->move_up();
if (final_node = process(new_node, open_map, open_set, close_map, target_map, alpha))
break;
else
++node_num;
}
if (node->zero_row < SIZE - 1) {
State* new_node = node->extend();
new_node->move_down();
if (final_node = process(new_node, open_map, open_set, close_map, target_map, alpha))
break;
else
++node_num;
}
if (node->zero_col > 0) {
State* new_node = node->extend();
new_node->move_left();
if (final_node = process(new_node, open_map, open_set, close_map, target_map, alpha))
break;
else
++node_num;
}
if (node->zero_col < SIZE - 1) {
State* new_node = node->extend();
new_node->move_right();
if (final_node = process(new_node, open_map, open_set, close_map, target_map, alpha))
break;
else
++node_num;
}
close_map.insert(pair<string, State*>(node->str_num, node));
}
end1 = clock();
cout << endl << "path: " << endl;
while (final_node) {
solution.push_front(final_node);
final_node = final_node->father;
}
int j = 0;
for (auto i = solution.begin(); i != solution.end(); ++i) {
cout << j++ << endl;
(*i)->show_table();
}
if (final_node)
cout << "solution depth: " << final_node->depth << endl;
std::cout << "node num: " << node_num << ", loop_num: " << loop_num << endl;
cout << "total time(s): " << (double)(end1 - start1) / CLOCKS_PER_SEC << endl;
return solution;
}
使用
int main()
{
table target = { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,0 };
table start = { 11,9,4,15,1,3,0,12,7,5,8,6,13,2,10,14 };
State* node0 = new State(start, 0);
deque<State*> solution = A_solution(node0, target, 0.5);
cout << solution.size() - 1<< endl;
return 0;
}
alpha为0.5的结果
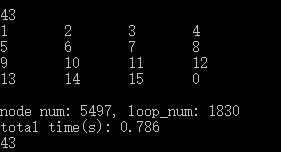
经过0.786秒输出结果,走了43步。
结果讨论
通过调整alpha值的大小,程序运行的速度有着显著差异。其中alpha为0.5时,程序运行最快;alpha为0.8时得到的解与alpha为1时相同,可视为最优解,最终解的深度为41。详细结果表格所示。但由于在算法设计中使用了按地址排序,因此结果会有一定的随机性,但程序按启发函数大小排序的约束不变,对于求解最优解的影响较小。
| alpha | 生成节点总数 | 循环总数 | 运行时间(s) | 解的深度 |
|---|---|---|---|---|
| 0.0 | 122080 | 41150 | 17.623 | 121 |
| 0.1 | 67870 | 22863 | 9.708 | 91 |
| 0.2 | 118769 | 39943 | 16.992 | 75 |
| 0.3 | 65107 | 21809 | 9.365 | 71 |
| 0.4 | 26386 | 8837 | 3.855 | 61 |
| 0.5 | 5318 | 1772 | 0.774 | 45 |
| 0.6 | 6779 | 2268 | 0.986 | 45 |
| 0.7 | 15190 | 5065 | 2.24 | 43 |
| 0.8 | 71747 | 23903 | 10.35 | 41 |
| 0.9 | 248572 | 82997 | 53.618 | 41 |
| 1.0 | 569932 | 189414 | 82.12 | 41 |
| 1.1 | 1051689 | 352964 | 152.168 | 41 |
| 1.2 | 2432141, | 812014 | 350.45 | 41 |
| 1.3 | 循环次数超出100,0000 | |||
| 从表 中可以看到,生成的节点总数、循环总数与运行时间是正相关的。而当alpha从0.1增大时,运行时间先减小再增大,在alpha为0.5时,程序运行最快,当alpha大于0.7后,程序运行时间快速增大。而解的深度则随着alpha增大而减小。 | ||||
| 可见,alpha越小,启发信息越强,同时程序也与趋向于局部最优,而陷入局部最优同样会浪费计算量,当alpha为0.5时达到了一个平衡,能以最快速度找到解。而随着alpha增大,算法越类似于广度优先搜索,越难找到解,计算量大大增加,同时找到解也越优。当alpha过大时,启发信息太弱,启发函数难以收敛,无法找到解。 |