Dubbo中的负载均衡算法之平滑加权轮询算法源码解析

Dubbo中的负载均衡算法之一致性哈希算法

哈希算法

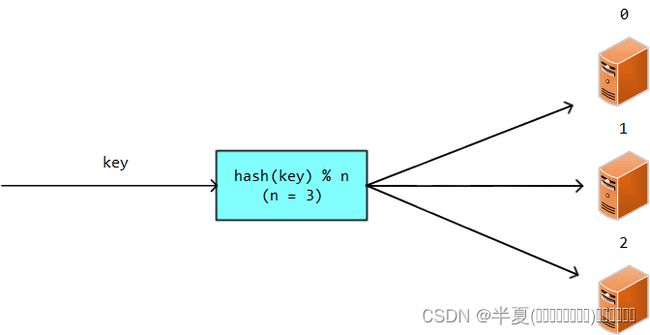
假设这样一个场景，我们申请一台服务器来缓存100万的数据，这个时候是单机环境，所有的请求都命中到这台服务器。后来业务量上涨，我们的数据也从100万上升到了300万，原来的单机环境，无法容纳如此多的数据，所以我们决定扩容到三台服务器。但这个时候有一个问题，这三百万的数据如何平均分配到这三台服务器上呢？假设我们随机分配，那么当我们需要查询某一个缓存项时，则需要先去第一台机器进行查找，如果找到则返回给用户，如果没有，继续去第二台机器查找，如果还没有则继续去第三台机器查找，这样一来，查询缓存项的性能则会明显下降，有没有办法根据缓存项的键，直接定位到正确的机器进行查询呢？

一种行之有效的方法就是通过哈希算法去定位。对于相同的键，每次计算得出的哈希值应该是一致的。假设我们有三台机器，可以对键通过哈希算法得到哈希值，然后对3取余，结果只能是0、1或2，我们将这三个结果分别作为三台机器的编号。这样每次有查询缓存的请求过来，我们都可以按照以下步骤去做

1. 对键进行哈希运算，得到一个哈希值，然后对3取余，得到一个机器编号
2. 前往对应的机器进行查询。如果找到缓存项，直接返回结果；如果未找到，表示缓存项不存在。
   

上述的方案看起来已经解决了问题，但是，如果在分布式场景中，却有着很大的局限性。因为在生产环境中，不可避免会发生以下几种情况：

1. 服务器故障宕机，无法提供服务而下线
2. 业务高峰期需要弹性扩容
3. 业务低谷期需要弹性缩容

这几种场景都会导致后台服务器的数量 n 发生变化，那么我们原来的公式hash(key) % n因为n发生了变化，导致计算出的值也会发生变化，这样一来就会导致大量的缓存失效，造成缓存雪崩。如果是采用这种方案做负载均衡的话，也会导致大量的请求路由到错误的服务器，找不到对应的服务，导致服务异常。因此就有了一致性hash算法，用来解决这个问题，保证当后端移除或者添加一个服务器时，要尽可能小的改变存量请求与服务器之间的正确映射关系。

一致性哈希算法

基本介绍

一致性哈希算法最早是由David Karger等人在1997年发表的论文Consistent Hashing and Random Trees: Distributed Caching Protocols for Relieving Hot Spots on the World Wide Web 中提出的。该算法的设计目标是为了解决因特网中的热点问题，即如何将数据尽可能均匀地分布到不同的节点上，以避免某些节点承受过大的负载。

它的主要思路是将整个哈希值空间组织成一个虚拟的圆环，让每个服务器节点在环上占据一个位置。有新的请求的时候，通过hash算法将请求映射到环上的一个位置，然后顺时针找到最近的服务器去进行处理。这样当一个服务器节点加入或退出时，只会影响到其附近的一小部分数据，而不会对整个系统造成很大的影响。他的一般步骤为：

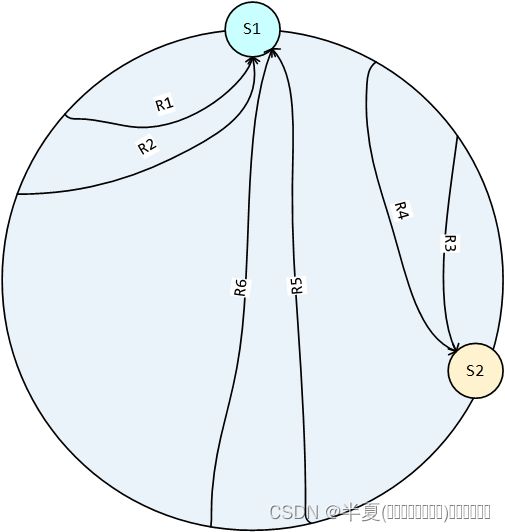
1. 如下图所示，我们虚拟出一个有2³²-1个节点的hash环，然后将服务器地址（ip+port）计算hash值,，对2³²-1取模，算出其在hash环上的位置，假设我们有三个服务器节点：S1、S2 、S3，其映射关系如图所示。
2. 当一个新的服务请求到来时，也对该请求的标识符进行哈希计算，得到其在环上的位置。
3. 从环上顺时针找到距离该请求最近的一个节点，将请求分配给该节点处理。例如请求R1,R2被分配给S1这个服务器去处理

如何解决服务器节点增加、减少带来的问题的

如果在hash环上加一个节点，例如我们添加了S4这个节点，那么原本应该路由到S1的请求和路由到S2的请求不会受到影响，依然可以正确路由，不过原本路由到S3的部分请求则将会被路由到新节点S4。这样就做到了我们前面说的尽可能小的改变已存在的服务请求与处理请求服务器之间的映射关系。

减少一个节点也是同样的道理，例如下图中我们下线了节点S3，那么原本应该路由到S1的请求和路由到S2的请求不会受到影响，依然可以正确路由，受影响的只是原本应该路由到S3的请求因为S3下线，而会路由到S1。

什么是虚拟节点

前面的图例中，我们可以看到S1，S2，S3三个节点是均匀分布在hash环上的，但是实际上，我们通过hash算法计算的时候可能达不到理想的效果，有可能会得到这样的分布效果。这就会导致大量的请求被路由到S3这个节点。因此提出了虚拟节点的概念。

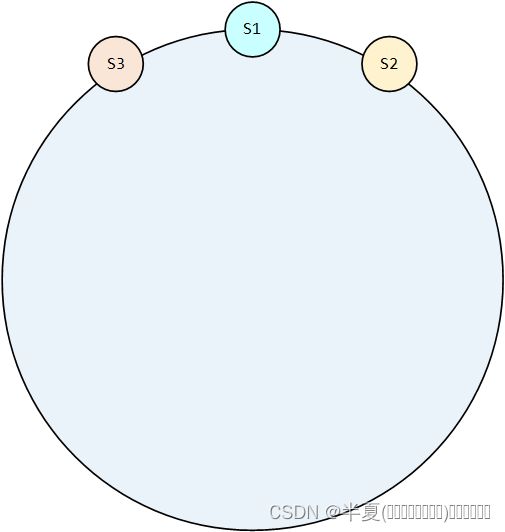
所谓虚拟节点就是说并非真实的物理节点，而是对物理节点拷贝的一个副本，他们和其对应的真实物理节点有一样的IP和端口号，因此称为虚拟节点。如下图所示，我们有三个物理节点，S1、S2、 S3。然后对每个物理节点虚拟出了两个虚拟节点，将其分布在hash环上。这样假设有一个请求访问过来，通过hash计算落到了S3-2到S2-2的区间，那么他将会路由到S2-2这个服务器节点，而S2-2其实是S2的一个虚拟节点，所以实际处理这个请求的是S2这个物理节点。通过图我们可以直观的看到，引入虚拟节点后，请求的分布会进一步变得平衡，而引入的虚拟节点数量越多，则平衡性越好。

Dubbo一致性哈希负载均衡的实现

dubbo一致性哈希负载均衡策略的实现在ConsistentHashLoadBalance这个类里，它继承了AbstractLoadBalance这个抽象类，实现了方法doSelect()方法，这个方法的作用是用来从多个服务提供者里面选择一个来调用。这里有两个重要的参数Invoker 和Invocation ，Invoker 我们可以理解为对服务提供者的一个封装，所有的服务提供者在dubbo里都会被转化为Invoker。所以List> invokers其实就是我们本次请求的所有服务提供者的列表。Invocation我们理解为对本次请求会话的一个封装，里面包括了请求的参数、方法以及变量

Invoker 和Invocation 的概念可参考：代码架构 | Apache Dubbo、实现细节 | Apache Dubbo

/**
 * 线程安全的一个map，缓存了所有的Selector（可以理解为一个选择器，用来从众多的服务提供者里面选择一个，实现负载均衡的效果），
 * key：服务提供者的签名
 * value：具体某一个服务对应的Selector
 */
private final ConcurrentMap<String, ConsistentHashSelector<?>> selectors = new ConcurrentHashMap<String, ConsistentHashSelector<?>>();

/**
 * 从invokers里选一个调用
 */
protected <T> Invoker<T> doSelect(List<Invoker<T>> invokers, URL url, Invocation invocation) {
    String methodName = RpcUtils.getMethodName(invocation);

    //  1. 根据服务提供者的签名从前面提到的map里找对应的选择器
    String key = invokers.get(0).getUrl().getServiceKey() + "." + methodName;
    int invokersHashCode = invokers.hashCode();
    ConsistentHashSelector<T> selector = (ConsistentHashSelector<T>) selectors.get(key);

    // 1.1  没有找到？那么初始化，这是一个懒加载的过程
    if (selector == null || selector.identityHashCode != invokersHashCode) {
        selectors.put(key, new ConsistentHashSelector<T>(invokers, methodName, invokersHashCode));
        selector = (ConsistentHashSelector<T>) selectors.get(key);
    }

    // 1.2 通过selector选一个具体的服务提供者，处理请求
    return selector.select(invocation);
}

前面提到如果没有找打对应的Selector，那么我们要去做初始化，这里是如何初始化一个一致性哈希负载均衡策略的逻辑。

private static final class ConsistentHashSelector<T> {
	
    // 用TreeMap模拟一个hash环
    private final TreeMap<Long, Invoker<T>> virtualInvokers;

    private final int replicaNumber;

    private final int identityHashCode;

    private final int[] argumentIndex;

    // 初始化Selector的逻辑
    ConsistentHashSelector(List<Invoker<T>> invokers, String methodName, int identityHashCode) {
        this.virtualInvokers = new TreeMap<Long, Invoker<T>>();
        this.identityHashCode = identityHashCode;
        URL url = invokers.get(0).getUrl();
        // 物理节点的副本数，默认160
        this.replicaNumber = url.getMethodParameter(methodName, HASH_NODES, 160);
        String[] index = COMMA_SPLIT_PATTERN.split(url.getMethodParameter(methodName, HASH_ARGUMENTS, "0"));
        argumentIndex = new int[index.length];
        for (int i = 0; i < index.length; i++) {
            argumentIndex[i] = Integer.parseInt(index[i]);
        }

        // 初始化hash环，将所有的invokers均匀的分布到环上
        for (Invoker<T> invoker : invokers) {
            String address = invoker.getUrl().getAddress();
            // 创建虚拟节点，每个物理机节点应该有replicaNumber个虚拟节点，但是这里用两次for循环，应该是为了加强hash的随机性
            for (int i = 0; i < replicaNumber / 4; i++) {
                byte[] digest = Bytes.getMD5(address + i);
                for (int h = 0; h < 4; h++) {
                    long m = hash(digest, h);
                    virtualInvokers.put(m, invoker);
                }
            }
        }
    }

    // 具体的选择逻辑，对请求计算md5值，算一个hash
    public Invoker<T> select(Invocation invocation) {
        byte[] digest = Bytes.getMD5(RpcUtils.getMethodName(invocation));
        return selectForKey(hash(digest, 0));
    }

    // 用ceilingEntry方法模拟从哈希环上选择顺时针最近的一个服务节点
    private Invoker<T> selectForKey(long hash) {
        Map.Entry<Long, Invoker<T>> entry = virtualInvokers.ceilingEntry(hash);
        if (entry == null) {
            entry = virtualInvokers.firstEntry();
        }
        return entry.getValue();
    }

    private long hash(byte[] digest, int number) {
        return (((long) (digest[3 + number * 4] & 0xFF) << 24)
                | ((long) (digest[2 + number * 4] & 0xFF) << 16)
                | ((long) (digest[1 + number * 4] & 0xFF) << 8)
                | (digest[number * 4] & 0xFF))
                & 0xFFFFFFFFL;
    }
}