【算法-LeetCode】611. 有效三角形的个数（排序；二分；双指针；回溯；递归）

611. 有效三角形的个数 - 力扣（LeetCode）

文章起笔：2021年11月17日24:13:04

问题描述及示例

给定一个包含非负整数的数组，你的任务是统计其中可以组成三角形三条边的三元组个数。

示例 1:
输入: [2,2,3,4]
输出: 3
解释:
有效的组合是:
2,3,4 (使用第一个 2)
2,3,4 (使用第二个 2)
2,2,3

注意:
数组长度不超过1000。
数组里整数的范围为 [0, 1000]。

我的题解

我的题解1（回溯；因超时而未通过）

看到题目的第一反应是用回溯的思想来做，本题其实可以看做是【组合问题】的一个变形，也就是从 nums 数组中任意选择三个数字作为一个组合，获取所有不重复的组合，并从这些组合中根据三角形的边的判断原则来决定哪些组合是符合要求的。有关回溯算法在组合问题中的应用，可以看下面的这篇文章：

参考：【算法-LeetCode】39. 组合总和（回溯；递归）_赖念安的博客-CSDN博客

本题的总体思路也和上面的差不多，只不过改变了一些关键的判断逻辑罢了。

输入题目本身提供的那个测试用例也能正确得到结果，于是我点击了提交。

/**
 * @param {number[]} nums
 * @return {number}
 */
var triangleNumber = function(nums) {
  let result = 0;
  // let result = [];
  let temp = [];
  backtrackting(nums, 0);
  return result;

  // backtrackting是用来作辅助的回溯函数，其主要逻辑其实就是寻找nums中的指定组合
  function backtrackting(nums, start) {
    // 递归终止条件，当temp中保存了三个元素时，就要判断一下这三个元素是否能够组成三角形
    // 如果能的话就让结果值加1，否则就保持原样，最后结束本层递归
    if(temp.length === 3) {
      // result.push([...temp]);
      result = isValid(...temp) ? result + 1 : result;
      return;
    }
    // 开始遍历nums数组，注意开始遍历的起点下标是由上一层递归指定的，这是组合问题的关键
    for(let i = start; i < nums.length; i++) {
      temp.push(nums[i]);
      backtrackting(nums, i+1);
      temp.pop();
    }
  }
  
  // isValid用来判断n1、n2、n3三个数能否组成有效的三角形
  function isValid(n1, n2, n3) {
    return n1 + n2 > n3 && n1 + n3 > n2 && n2 + n3 > n1;
  }
};


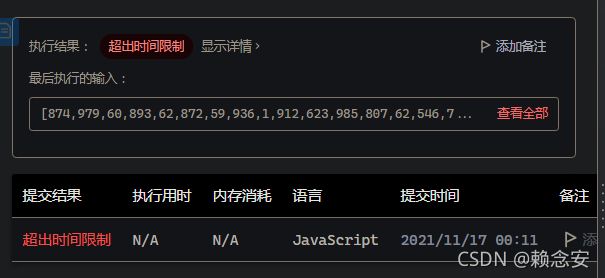
执行结果：超出时间限制
最后执行的输入：
[874,979,60,893,62,872,59,936,1,912,623,...,102,884,325,408,248,493,550]
时间：2021/11/17 00:13

但是却发现下面的这个较长的用例没法儿通过：

执行结果：超出时间限制
最后执行的输入：
[874,979,60,893,62,872,59,936,1,912,623,...,102,884,325,408,248,493,550]
时间：2021/11/17 00:13

显示的信息是：超出时间限制

于是我根据以往做回溯题目时的经验就猜想可能是由于自己没有做相应的枝剪操作，于是尝试加上了下面代码，看能不能起到枝剪的效果：

// 以下判断不能起到枝剪的作用
if (temp.length === 3 && !isValid(...temp)) {
  continue;
}

结果发现还是超时：

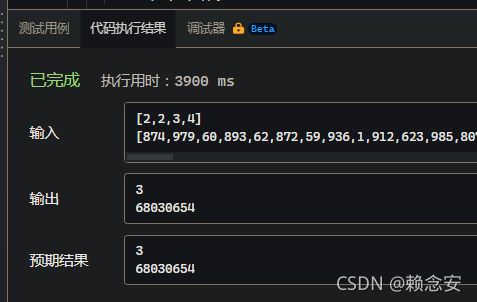
不过我把这个较长用例输入用例框中时却发现可以得到正确的预期结果：

说明逻辑是正确的，但是上面的枝剪操作并没有起什么作用。

太晚了，睡觉吧~

我的题解2（排序；二分）

更新：2021年11月17日15:35:32

昨天尝试了用回溯的思想来寻找有效的组合。但是发现会超时。于是我又想到之前做过的一道判断三数之和的问题：

参考：【算法-LeetCode】15. 三数之和（双指针）_赖念安的博客-CSDN博客

上面这道题也是针对三个数的大小关系进行的思考。于是我就想也许本题也能找到一些灵感。事实上我也确实找到了一点门道，而且发现了比较关键的操作：对原数组的排序操作。但是在寻找有效的第三条边时，我遇到了瓶颈，程序始终没有通过。一开始我没有想到用二分法来做，后来是看到了【官方题解】里的思路才意识到可以利用二分来完成。

上面提到要对原数组做排序操作，这个排序操作是后面逻辑的基石。这个排序操作使得我们对三角形边的有效性的判断由原先的需要同时满足三个条件变为只要满足一个条件。这就大大简化了流程。

这种排序后再进行元素搜索的操作和上面提到的【三数之和】中的思路有异曲同工之处，可以对照思考。

相关的逻辑在【官方题解】都有详细的描述，建议之间参考官方题解。

/**
 * @param {number[]} nums
 * @return {number}
 */
var triangleNumber = function (nums) {
  // 一定要先对nums做排序操作，这是后面操作的基础
  nums.sort((a, b) => a - b);
  // 我一开始没有注意到temp变量的作用，所以特意在遍历开始前对nums数组进行了去零操作
  // // 预先把头部的0给剔除
  // while (nums[0] === 0) {
  //   nums.shift();
  // }
  // // 如果发现nums中的元素个数少于三个，可以直接提前返回0
  // if (nums.length < 3) {
  //   return 0;
  // }
  let result = 0;
  // 下面的双层for循环就相当于是确定了三角形中的两条边，而里面的while循环就是在寻找第三边
  for (let i = 0; i < nums.length; i++) {
    for (let j = i + 1; j < nums.length; j++) {
      let front = j + 1;
      let back = nums.length - 1;
      let mid = 0;
      // 注意temp遍历的作用，它不仅可以保存mid的值，还可以用来应对nums中有0的情况
      let temp = j;
      // 下面的while循环就是二分的逻辑，一定要注意边界条件的判断
      while (front <= back) {
        mid = Math.floor((back - front) / 2 + front);
        if (nums[mid] < nums[i] + nums[j]) {
          temp = mid;
          front = mid + 1;
        } else {
          back = mid - 1;
        }
      }
      result = result + temp - j;
    }
  }
  return result;
};


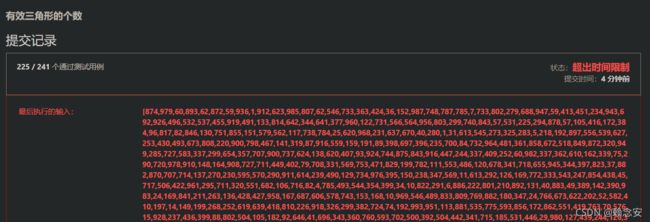
提交记录
执行结果：通过
执行用时：536 ms, 在所有 JavaScript 提交中击败了29.97%的用户
内存消耗：39.2 MB, 在所有 JavaScript 提交中击败了90.49%的用户
通过测试用例：241 / 241
时间：2021/11/17 15:30

官方题解

更新：2021年7月29日18:43:21

因为我考虑到著作权归属问题，所以【官方题解】部分我不再粘贴具体的代码了，可到下方的链接中查看。

【更新结束】

更新：2021年11月17日15:34:10

参考：有效三角形的个数 - 有效三角形的个数 - 力扣（LeetCode）

【更新结束】

有关参考

更新：2021年11月17日24:47:30
参考：【算法-LeetCode】39. 组合总和（回溯；递归）_赖念安的博客-CSDN博客
更新：2021年11月17日15:34:58
参考：【算法-LeetCode】704. 二分查找_赖念安的博客-CSDN博客
参考：【算法-LeetCode】15. 三数之和（双指针）_赖念安的博客-CSDN博客