现代密码学第三次实验:不对称加密算法RSA
现代密码学第三次实验:不对称加密算法RSA
- 前言
- 一、实验目的
- 二、实验环境
- 三、实验步骤
- 四、实验基本方法
- 五、实验程序清单
- 七、实验结果
- 八、实验总结
前言
为了帮助同学们完成痛苦的实验课程设计,本作者将其作出的实验结果及代码贴至CSDN中,供同学们学习参考。如有不足或描述不完善之处,敬请各位指出,欢迎各位的斧正!
一、实验目的
1、掌握RSA算法的工作原理。
2、熟悉利用素性检测找素数的工作原理。
3、熟悉商业开发时RSA算法的应用。
二、实验环境
Microsoft Visual Studio 2019
三、实验步骤
1.编程实现找素数的算法。
2.编程实现找RSA参数的计算程序。
3.编写一个RSA算法;
4.对2个字符加、解密,改变最低1位明文观察并记录RSA的输出。
5.对2个字符加、解密,改变最高1位明文观察并记录RSA的输出。
6.使用VS平台,以framework为基础,编写RSA加解密程序,观测密钥容器、密钥的产生、导出和导入
四、实验基本方法
1、用C或C++语言编写找素数的算法,并编写RSA参数的计算程序,并将结果显示显示在屏幕上。
2、用C或C++语言编写一个RSA算法,实现其中各关键算法:求逆元、模幂运算(快速指数算法)等;
3、编程实现对32位二进数(3个字符)的加、解密;
4、手工验证加、解密的结果。
5、使用VS平台,以framework为基础,编写RSA加解密程序。
说明:
RSA算法可以自编,也可以网上下载现成算法。
五、实验程序清单
1.程序设计的思想,及程序关键原代码。(见实验程序清单)
2.说明素性检测的原理。(见实验总结)
3.说明RSA参数的e、d计算的原理。(见实验总结)
4.报告对2个字符加、解密,改变最高低和最低1位明文RSA的输出结果。(见实验结果)
5.分析上述输出的原因,手工验证输出的正确性。
6.描述使用framework编写RSA加解密程序的关键点和要注意的问题。
源代码修改如下:
// RSA_sView.cpp : implementation of the CRSA_sView class
//
#include "stdafx.h"
#include "RSA_s.h"
#include "RSA_sDoc.h"
#include "RSA_sView.h"
#ifdef _DEBUG
#define new DEBUG_NEW
#undef THIS_FILE
static char THIS_FILE[] = __FILE__;
#endif
/
// CRSA_sView
IMPLEMENT_DYNCREATE(CRSA_sView, CFormView)
BEGIN_MESSAGE_MAP(CRSA_sView, CFormView)
//{{AFX_MSG_MAP(CRSA_sView)
ON_BN_CLICKED(IDC_BUTTON1_E, OnButton1E)
ON_BN_CLICKED(IDC_BUTTON1_D, OnButton1D)
ON_BN_CLICKED(IDC_BUTTON1_p, OnBUTTON1p)
ON_BN_CLICKED(IDC_BUTTON1_q, OnBUTTON1q)
ON_BN_CLICKED(IDC_BUTTON1_PARA, OnButton1Para)
//}}AFX_MSG_MAP
// Standard printing commands
ON_COMMAND(ID_FILE_PRINT, CFormView::OnFilePrint)
ON_COMMAND(ID_FILE_PRINT_DIRECT, CFormView::OnFilePrint)
ON_COMMAND(ID_FILE_PRINT_PREVIEW, CFormView::OnFilePrintPreview)
END_MESSAGE_MAP()
/
// CRSA_sView construction/destruction
CRSA_sView::CRSA_sView()
: CFormView(CRSA_sView::IDD)
{
//{{AFX_DATA_INIT(CRSA_sView)
m_p = _T("");
m_md = _T("");
m_cd = _T("");
m_m1d = _T("");
m_q = _T("");
m_n = _T("");
m_e = _T("");
m_d = _T("");
m_fn = _T("");
m_m = _T("");
m_c = _T("");
m_m1 = _T("");
//}}AFX_DATA_INIT
// TODO: add construction code here
}
CRSA_sView::~CRSA_sView()
{
}
void CRSA_sView::DoDataExchange(CDataExchange* pDX)
{
CFormView::DoDataExchange(pDX);
//{{AFX_DATA_MAP(CRSA_sView)
DDX_Text(pDX, IDC_EDIT1_p, m_p);
DDX_Text(pDX, IDC_EDIT10_md, m_md);
DDX_Text(pDX, IDC_EDIT11_cd, m_cd);
DDX_Text(pDX, IDC_EDIT12_m1d, m_m1d);
DDX_Text(pDX, IDC_EDIT2_q, m_q);
DDX_Text(pDX, IDC_EDIT3_n, m_n);
DDX_Text(pDX, IDC_EDIT4_e, m_e);
DDX_Text(pDX, IDC_EDIT5_d, m_d);
DDX_Text(pDX, IDC_EDIT6_fn, m_fn);
DDX_Text(pDX, IDC_EDIT7_m, m_m);
DDX_Text(pDX, IDC_EDIT8_c, m_c);
DDX_Text(pDX, IDC_EDIT9_m1, m_m1);
//}}AFX_DATA_MAP
}
BOOL CRSA_sView::PreCreateWindow(CREATESTRUCT& cs)
{
// TODO: Modify the Window class or styles here by modifying
// the CREATESTRUCT cs
return CFormView::PreCreateWindow(cs);
}
void CRSA_sView::OnInitialUpdate()
{
CFormView::OnInitialUpdate();
GetParentFrame()->RecalcLayout();
ResizeParentToFit();
}
/
// CRSA_sView printing
BOOL CRSA_sView::OnPreparePrinting(CPrintInfo* pInfo)
{
// default preparation
return DoPreparePrinting(pInfo);
}
void CRSA_sView::OnBeginPrinting(CDC* /*pDC*/, CPrintInfo* /*pInfo*/)
{
// TODO: add extra initialization before printing
}
void CRSA_sView::OnEndPrinting(CDC* /*pDC*/, CPrintInfo* /*pInfo*/)
{
// TODO: add cleanup after printing
}
void CRSA_sView::OnPrint(CDC* pDC, CPrintInfo* /*pInfo*/)
{
// TODO: add customized printing code here
}
/
// CRSA_sView diagnostics
#ifdef _DEBUG
void CRSA_sView::AssertValid() const
{
CFormView::AssertValid();
}
void CRSA_sView::Dump(CDumpContext& dc) const
{
CFormView::Dump(dc);
}
CRSA_sDoc* CRSA_sView::GetDocument() // non-debug version is inline
{
ASSERT(m_pDocument->IsKindOf(RUNTIME_CLASS(CRSA_sDoc)));
return (CRSA_sDoc*)m_pDocument;
}
#endif //_DEBUG
/
// CRSA_sView message handlers
unsigned long int CRSA_sView::M_R(unsigned long m,unsigned long n) //Miller--Rabin素性检测法找素数,产生m~n之间的一个素数
{
unsigned long int p;
int i,f=0;
for(;;)
{
f=0;
p=random(m,n);
if(p%2==0) p=p-1;
for(i=0;i<50;i++)
{
if(RabinMillerKnl(p)==1)
f++;
}
if(f==50)
return p;
}
}
//随机数产生器,产生m~n之间的一个随机数
unsigned long CRSA_sView::random(unsigned long m,unsigned long n)
{
srand((unsigned long)time(NULL));
return (unsigned long)(m+rand()%n);
}
//Rabin-Miller素数测试,通过测试返回1,否则返回0。 n是待测素数。
int CRSA_sView::RabinMillerKnl(unsigned long n)
{
unsigned long b, m, j, v, i;
m=n-1; //先计算出m、j,使得n-1=m*2^j,其中m是正奇数,j是非负整数
j=0;
while(!(m&1))
{
++j;
m>>=1;
}
b=random(2,m); //随机取一个b,2<=b
v=(unsigned long)mod(b, m, n); //计算v=b^m mod n
if(v == 1) //如果v==1,通过测试
{
return 1;
}
i=1;
while(v != n - 1) //如果v=n-1,通过测试
{
if(i == j) //如果i==l,非素数,结束
{
return 0;
}
v=(unsigned long)mod(v, 2, n); //v=v^2 mod n,i=i+1
i++;
}
return 1;
}
unsigned long int CRSA_sView::inverse(unsigned long x,unsigned long n1) //扩展欧基里德算法——求逆元
{
long int x1,x2,x3,y1,y2,y3,q,t1,t2,t3;
x1=1;x2=0;x3=n1;
y1=0;y2=1;y3=x;
for(;;)
{
if(y3==0)
{
x3=gcd(n1,x);
return 0; //没有逆元
}
if(y3==1)
{
y3=gcd(n1,x);
if(y2<0) return n1+y2;
else
return y2;
}
q=x3/y3;
t1=x1-q*y1; t2=x2-q*y2; t3=x3-q*y3;
x1=y1; x2=y2; x3=y3;
y1=t1; y2=t2; y3=t3;
}
}
unsigned long int CRSA_sView::gcd(unsigned long x,unsigned long y) //欧基里德算法——求最大公约数
{
unsigned long int r;
for(;;)
{
if(x%y==0) return y;
if(y%x==0) return x;
r=x%y;
x=y;
y=r;
}
}
//指数取模:a的b次方modc=x
_int64 CRSA_sView::mod(_int64 a,_int64 b,_int64 c)//(a)^bmod(c)//条件1:在rsa中a
{
_int64 l[500],z=-1,y;
for(;b!=1;b>>=1)//分解b为2进制数.记录下分解成的位数z,构造栈l
{
z++;
if(b%2==0) l[z]=0;
else l[z]=1;
}
//a%=c;//如果一开始数就很大,先模一次,防止过大, 求逆
y=a*a%c;//第一次模
for(;z>0;z--)
{
if(l[z]) y=(y*a%c)*(y*a%c)%c;
else y=y*y%c;
}
if(l[0]) y=(y*a%c);//最后次模
return y;
}
unsigned long int CRSA_sView::StrToULong(CString s) //3个字符的字符串转整数
{
unsigned long int a;
char c1,c2,c3,*p;
p=s.GetBuffer(s.GetLength());
c1=p[0];
c2=p[1];
c3=p[2];
a=c1*256*256+c2*256+c3;
return a;
}
CString CRSA_sView::ULongToString(unsigned long int d) //整数转3个字符的字符串
{
CString a,b,c,xx;
unsigned char c1,c2,c3,c4;
c3=unsigned char(d);
c2=unsigned char(d/(256));
c1=unsigned char(d/(256*256));
a.Format("%c",c1);
b.Format("%c",c2);
c.Format("%c",c3);
a=a+b+c+xx;
return a;
}
void CRSA_sView::OnButton1E() //加密
{
// TODO: Add your control notification handler code here
UpdateData(TRUE);
m=StrToULong(m_m);
m_md.Format("%lu",m);
c=(unsigned long)mod(m,e,n);
m_c=ULongToString(c);
m_cd.Format("%lu",c);
UpdateData(FALSE);
}
void CRSA_sView::OnButton1D() //解密
{
// TODO: Add your control notification handler code here
m1=(unsigned long)mod(c,d,n);
m_m1=ULongToString(m1);
m_m1d.Format("%lu",m1);
UpdateData(FALSE);
}
void CRSA_sView::OnBUTTON1p() //寻找p
{
// TODO: Add your control notification handler code here
p=M_R(32768,65535);
m_p.Format("%lu",p);
UpdateData(FALSE);
}
void CRSA_sView::OnBUTTON1q() //寻找q
{
// TODO: Add your control notification handler code here
q=M_R(8192,16384);
m_q.Format("%lu",q);
UpdateData(FALSE);
}
void CRSA_sView::OnButton1Para() //参数计算
{
// TODO: Add your control notification handler code here
n=p*q;
fn=(p-1)*(q-1);
for(;;) //寻找e
{
e=random(128,256);
if(gcd(e,fn)==1)
break;
}
d=inverse(e,fn); //计算d
m_n.Format("%lu",n);
m_e.Format("%lu",e);
m_d.Format("%lu",d);
m_fn.Format("%lu",fn);
UpdateData(FALSE);
}
源代码修改如下:
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Windows.Forms;
using System.Security.Cryptography;
using System.IO;
namespace RSATest
{
public partial class Form1 : Form
{
public Form1()
{
InitializeComponent();
}
private void button1_Click(object sender, EventArgs e)
{
var cspPas = new CspParameters();
cspPas.KeyContainerName = "rsa_key";
RSACryptoServiceProvider RSA1 = new RSACryptoServiceProvider(cspPas);
RSA1.PersistKeyInCsp = false;
RSA1.Clear();
RSACryptoServiceProvider RSA = new RSACryptoServiceProvider(cspPas);
string str_Public_Key;
string str_Private_Key;
str_Public_Key = "";
str_Private_Key = "";
str_Public_Key = Convert.ToBase64String(RSA.ExportCspBlob(false));
str_Private_Key = Convert.ToBase64String(RSA.ExportCspBlob(true));
textBox1.Text = str_Public_Key;
textBox2.Text = str_Private_Key;
}
private void label2_Click(object sender, EventArgs e)
{
}
private void button2_Click(object sender, EventArgs e)
{
var cspPas = new CspParameters();
cspPas.KeyContainerName = "rsa_key";
RSACryptoServiceProvider RSA = new RSACryptoServiceProvider(cspPas);
FileStream fs1 = new FileStream("E:\\学习\\学习\\密码学\\密码学实验\\第三次\\RSATest\\RsaKey1.dat", FileMode.Create, FileAccess.Write);
string key = RSA.ToXmlString(false);
fs1.Write(Encoding.UTF8.GetBytes(key), 0, key.Length);
fs1.Close();
fs1.Dispose();
FileStream fs2 = new FileStream("E:\\学习\\学习\\密码学\\密码学实验\\第三次\\RSATest\\RsaKey2.dat", FileMode.Create, FileAccess.Write);
key = RSA.ToXmlString(true);
fs2.Write(Encoding.UTF8.GetBytes(key), 0, key.Length);
fs2.Close();
fs2.Dispose();
}
private void button3_Click(object sender, EventArgs e)
{
byte[] cipherbytes;
var cspPas = new CspParameters();
cspPas.KeyContainerName = "rsa_key";
RSACryptoServiceProvider RSA = new RSACryptoServiceProvider(cspPas);
cipherbytes = RSA.Encrypt(Encoding.Default.GetBytes(textBox3.Text), false);//RSA_PKCS1_PADDING
textBox4.Text = Convert.ToBase64String(cipherbytes);
}
private void button4_Click(object sender, EventArgs e)
{
byte[] cipherbytes1;
byte[] cipherbytes2;
var cspPas = new CspParameters();
cspPas.KeyContainerName = "rsa_key";
RSACryptoServiceProvider RSA = new RSACryptoServiceProvider(cspPas);
cipherbytes2 = Convert.FromBase64String(textBox4.Text);
cipherbytes1 = RSA.Decrypt(cipherbytes2, false);
textBox5.Text = Encoding.Default.GetString(cipherbytes1);
}
private void button5_Click(object sender, EventArgs e)
{
byte[] bin = new byte[1000];
var cspPas = new CspParameters();
cspPas.KeyContainerName = "rsa_key";
RSACryptoServiceProvider RSA = new RSACryptoServiceProvider(cspPas);
FileStream fs1 = new FileStream("E:\\学习\\学习\\密码学\\密码学实验\\第三次\\RSATest\\RsaKey1.dat", FileMode.Open, FileAccess.Read);
string key;
string str_Public_Key;
fs1.Read(bin, 0, 1000);
key = System.Text.Encoding.Default.GetString(bin);
fs1.Close();
fs1.Dispose();
RSA.FromXmlString(key);
str_Public_Key = "";
str_Public_Key = Convert.ToBase64String(RSA.ExportCspBlob(false));
textBox1.Text = str_Public_Key;
textBox2.Text = "";
}
private void button6_Click(object sender, EventArgs e)
{
byte[] bin = new byte[1000];
var cspPas = new CspParameters();
cspPas.KeyContainerName = "rsa_key";
RSACryptoServiceProvider RSA = new RSACryptoServiceProvider(cspPas);
FileStream fs1 = new FileStream("E:\\学习\\学习\\密码学\\密码学实验\\第三次\\RSATest\\RsaKey2.dat", FileMode.Open, FileAccess.Read);
string key;
string str_Public_Key;
string str_Private_Key;
fs1.Read(bin, 0, 1000);
key = System.Text.Encoding.Default.GetString(bin);
fs1.Close();
fs1.Dispose();
RSA.FromXmlString(key);
str_Public_Key = "";
str_Private_Key = "";
str_Public_Key = Convert.ToBase64String(RSA.ExportCspBlob(false));
str_Private_Key = Convert.ToBase64String(RSA.ExportCspBlob(true));
textBox1.Text = str_Public_Key;
textBox2.Text = str_Private_Key;
}
private void button7_Click(object sender, EventArgs e)
{
byte[] bin = new byte[1000];
var cspPas = new CspParameters();
cspPas.KeyContainerName = "rsa_key";
RSACryptoServiceProvider RSA = new RSACryptoServiceProvider(cspPas);
FileStream fs1 = new FileStream("E:\\学习\\学习\\密码学\\密码学实验\\第三次\\RSATest\\RsaKey1.dat", FileMode.Open, FileAccess.Read);
string key;
string str_Public_Key;
fs1.Read(bin, 0, 1000);
key = System.Text.Encoding.Default.GetString(bin);
fs1.Close();
fs1.Dispose();
RSA.FromXmlString(key);
str_Public_Key = "";
str_Public_Key = Convert.ToBase64String(RSA.ExportCspBlob(false));
textBox1.Text = str_Public_Key;
textBox2.Text = "";
byte[] bin1 = new byte[1000];
var cspPas1 = new CspParameters();
cspPas1.KeyContainerName = "rsa_key";
RSACryptoServiceProvider RSA1 = new RSACryptoServiceProvider(cspPas1);
FileStream fs11 = new FileStream("E:\\学习\\学习\\密码学\\密码学实验\\第三次\\RSATest\\RsaKey2.dat", FileMode.Open, FileAccess.Read);
string key1;
string str_Public_Key1;
string str_Private_Key1;
fs11.Read(bin1, 0, 1000);
key1 = System.Text.Encoding.Default.GetString(bin1);
fs11.Close();
fs11.Dispose();
RSA1.FromXmlString(key1);
str_Private_Key1 = "";
str_Public_Key1 = Convert.ToBase64String(RSA1.ExportCspBlob(false));
str_Private_Key1 = Convert.ToBase64String(RSA1.ExportCspBlob(true));
textBox2.Text = str_Private_Key1;
}
}
}
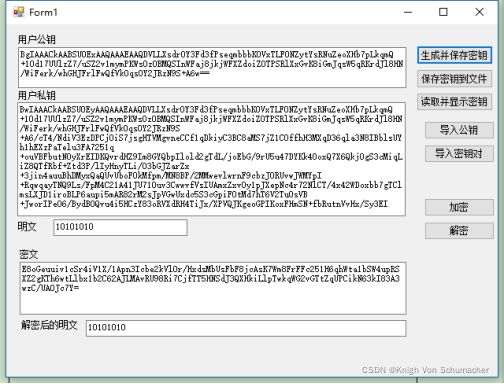
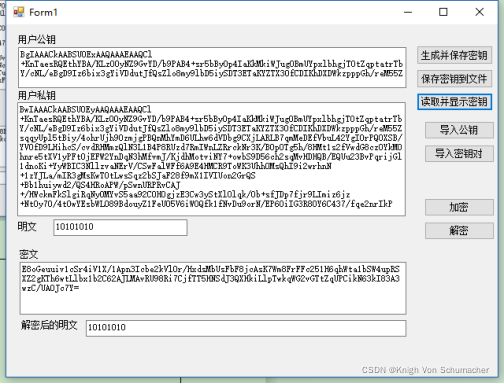
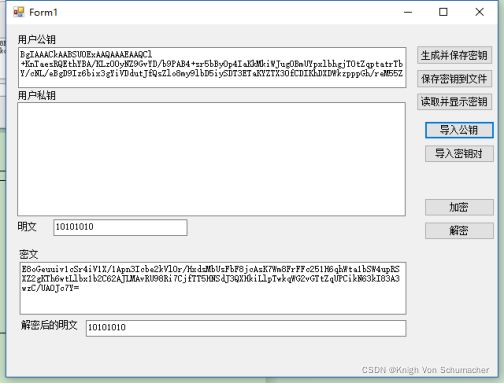
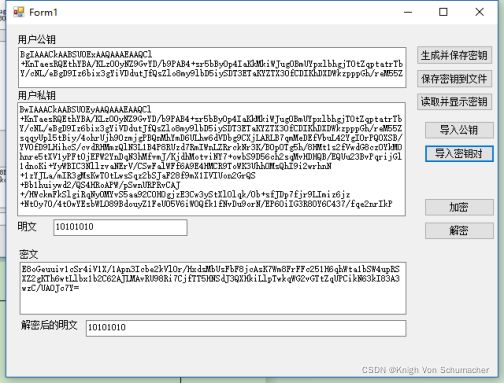
编辑MFC对话框如下:(添加button控件“读取并显示密钥”)
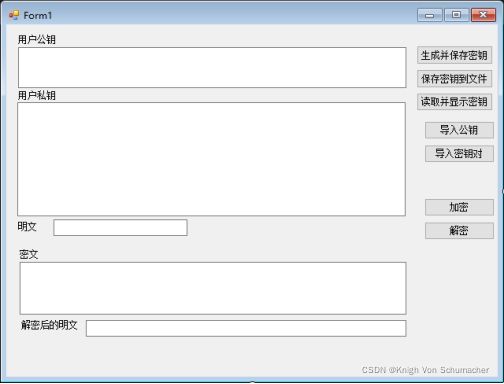
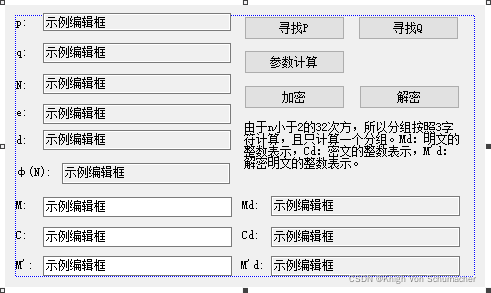
七、实验结果
寻找P:

寻找Q:
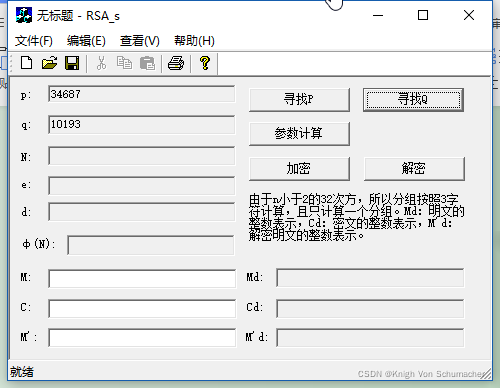
参数计算:
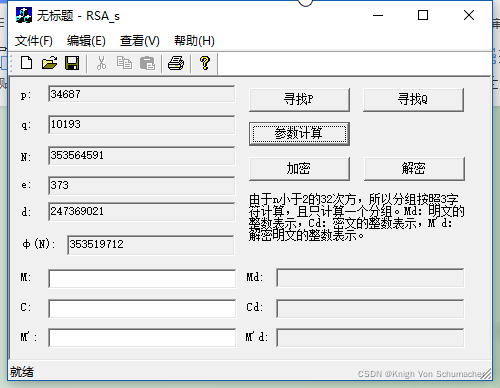
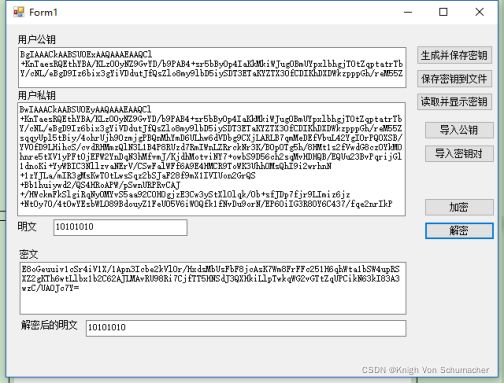
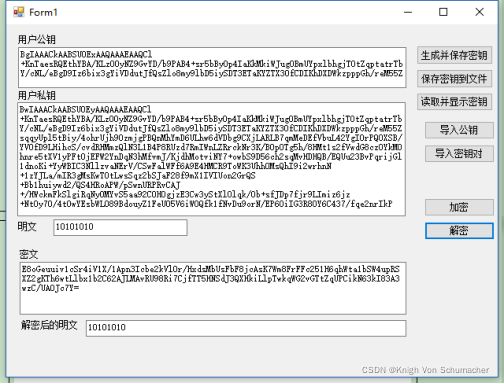
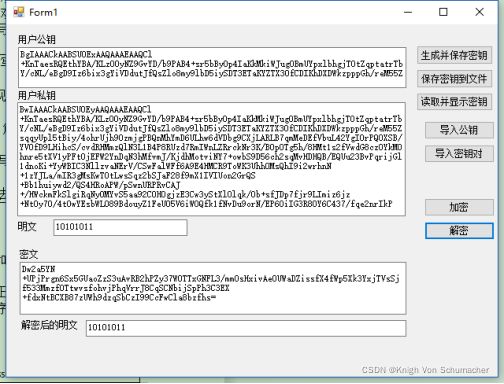
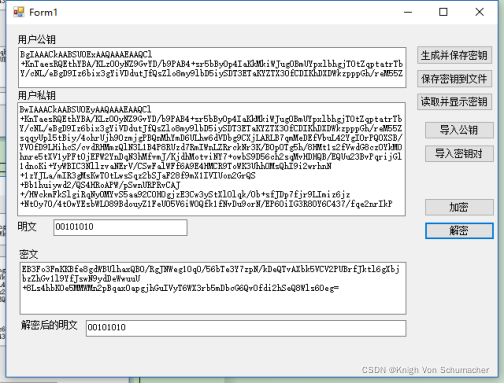
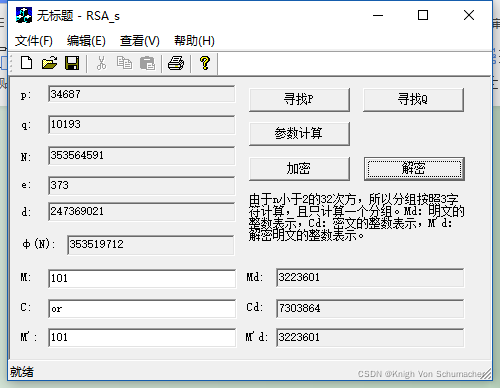
输入数据进行加解密:
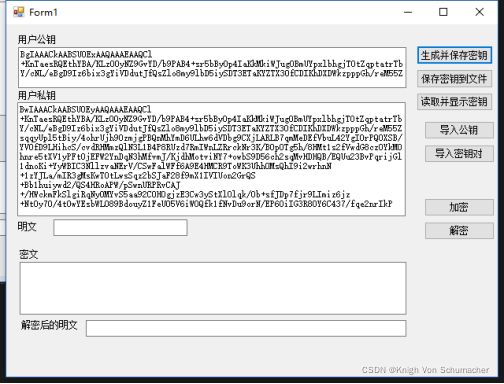
生成并保存密钥
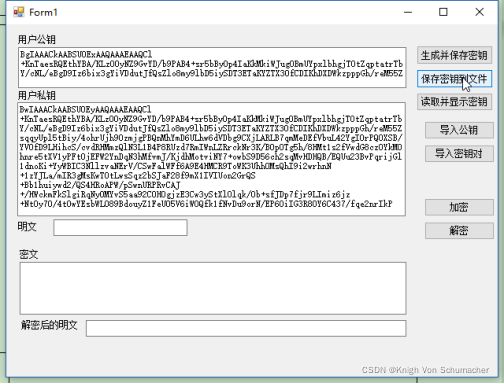
保存密钥到文件
八、实验总结
2.说明素性检测的原理。
答:由于本实验采用的素性检测是Miller-Rabin概率检测法,所以着重叙述此检测法的原理。
对s个不同的a重复调用Miller-Rabin算法,只要有一次算法返回为FALSE,就可肯定n不是素数。如果算法每次返回都为TRUE,则n是素数的概率至少为1-2-S,因此对于足够大的s,就可以非常肯定的相信n为素数。
3.说明RSA参数的e、d计算的原理。
答:利用上题所提到的Miller-Rabin概率检测法,我们寻找p为范围在32768到65535之间的一个大素数,寻找q为范围在8192到16384之间的一个大素数。
令n=pq,fn=(p-1)(q-1),寻找一个范围在128到256之间的一个随机数e,使其与fn互素,最终利用扩展欧基里德算法求e与fn两者的逆元d,即可计算出e、d。
5.分析上述输出的原因,手工验证输出的正确性。
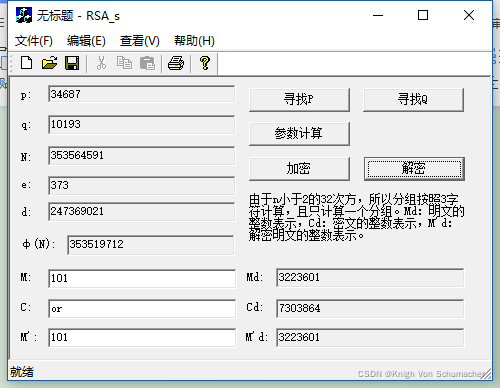
n=3468710193=353564591
fn=(34687-1)(10193-1)=353519712
生成随机数e=373与fn=353519712互素
可求得e=373与fn=353519712之间的逆元d=247369021
公钥(353564591,373),私钥(353564591,247369021)
Cd=Mde (mod fn)=3223601373 mod 353564591=7303864
M’d=Cde (mod fn)=7303864373 mod 353564591=3223601
6.描述使用framework编写RSA加解密程序的关键点和要注意的问题。
/// 分段加解密时:如果加密时设置的长度不匹配,可能会报以下错误:
crypto.BadPaddingException : Decryption error //解码失败