数据结构及底层原理实现

区分物理结构和逻辑结构

物理结构：数据在内存中的真实存储方式

逻辑结构：是一个抽象的概念，可以说是在物理结构的基础上“想象”出来的一种数据存储格式。

常见数据结构分类：

逻辑结构		物理结构
线性结构	非线性结构	顺序存储结构	链式存储结构
顺序表、栈、队列	树、图	数组	链表

物理结构介绍

数组

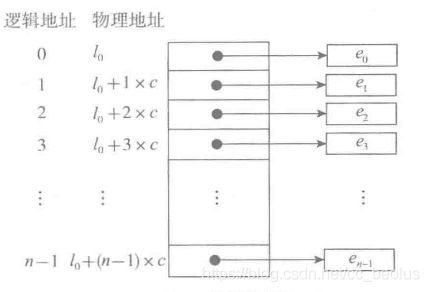
什么是数组： 是有限个相同数据类型的元素组成的有序集合，称之为数组。数组在内存中是顺序存储的，内存是由一个个连续的内存单元组成，每一个内存单元都有对应的地址，而数组中的每一个元素之间是存储在一片连续的内存单元，中间不会跳过某个存储单元。

如下图所示：

数组的操作：

• 查询：根据下标读取元素，称之为随机读取，数组的查询元素时间复杂为O(1);
• 更新：数组更新某一个元素的时间复杂度为O(1);
• 尾部插入：在数组空间充足情况下，尾部插入时间复杂度为O(1);
• 中间插入：在中间位置插入元素，被插入位置后面的所有元素都要向后移动，所以时间复杂度为O(N);
• 超出范围插入：当前数组的无空闲的空间，再插入新的数据时，需要动态扩容，时间复杂度为O(N)；
• 删除元素：删除某一个元素，被删除元素位置后的元素需要往前移动，时间复杂度为O(N)。

链表

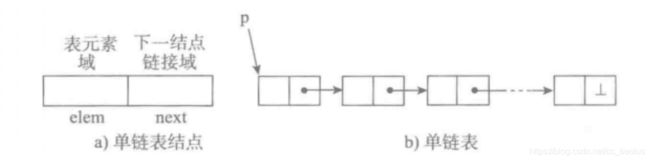
什么是链表： 链表是一种在物理上非连续、非顺序的数据结构，由若干个节点(node)组成。每一个节点包括存放数据的变量和指向下一个节点的指针。链表在内存中是随机存储的，每个节点分布在内存的不同位置，依靠next指针关联起来。

单向链表：

双向链表：

循环链表：

链表的操作和代码实现（以单链表为例）：

class SingleNode(object):
    """定义单节点"""
    def __init__(self, item):
        self.item = item
        self.next = None


class SingleLinkList(object):
	"""定义一个单向链表"""
    def __init__(self):
        self.__head = None

    def is_empty(self):
        """判断链表是否为空"""
        return self.__head is None

    def length(self):
        """返回链表元素个数"""
        import itertools
        dummy = self.__head
        count = itertools.count()
        while dummy:
            dummy = dummy.next
            next(count)
        return next(count)

    def travel(self):
        """遍历链表"""
        dummy = self.__head
        while dummy:
            print(dummy.item)
            dummy = dummy.next

    def add(self, item):
        """头部添加元素"""
        node = SingleNode(item)
        node.next = self.__head
        self.__head = node

    def append(self, item):
        """尾部添加元素"""
        node = SingleNode(item)
        if self.is_empty():
            self.__head = node
        else:
            dummy = self.__head
            while dummy.next is not None:
                dummy = dummy.next
            dummy.next = node

    def insert(self, pos, item):
        """指定位置插入元素"""
        if pos <= 0:
            self.add(item)
        elif pos >= self.length():
            self.append(item)
        else:
            node = SingleNode(item)
            count = 1
            dummy = self.__head
            while count < pos:
                dummy = dummy.next
                count += 1
            node.next = dummy.next
            dummy.next = node

    def remove(self, item):
        """删除元素"""
        cur = self.__head
        prev = None
        while cur:
            if cur.item == item:
                if cur is self.__head:
                    self.__head = cur.next
                else:
                    prev.next = cur.next
                break
            else:
                prev, cur = cur, cur.next

    def search(self, item):
        """查询某节点是否存在"""
        dummy = self.__head
        while dummy:
            if dummy.item == item:
                return True
            else:
                dummy = dummy.next
        return False

数组和链表的区别

数组与链表基本操作的性能比较：

\	查找	更新	插入	删除
数组	O(1)	O(n)	O(n)	O(n)
链表	O(n)	O(1)	O(1)	O(1)

tips:数组的查询很快，有时候主要耗时是扩容、数据迁移操作；链表的主要耗时是遍历查找，更新、插入和删除本身的操作是O(1).

逻辑结构介绍

栈(stack)

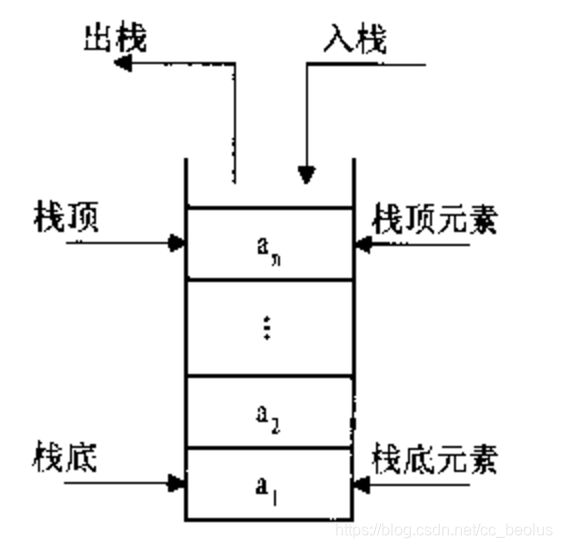
什么是栈： 栈是一种线性数据结构，栈相对一个容器，最早先放进去的元素的位置叫栈底，最后放进去的元素的位置叫栈顶，栈中的元素取出的规律是：后进先出。入栈和出栈只能通过栈顶进出。栈的实现可以通过数组或链表。

如下图所示：

栈的基本操作和代码实现：

# 使用顺序表实现栈
class ArrayStack(object):
    def __init__(self):
        self.items = []

    def is_empty(self):
        """判断栈元素是否为空"""
        return self.items == []

    def push(self, item):
        """元素入栈"""
        self.items.append(item)

    def pop(self):
        """元素出栈"""
        return self.items.pop()

    def peek(self):
        """返回栈顶元素"""
        return self.items[-1]

    def size(self):
        """栈的元素个数"""
        return len(self.items)


# 使用链表实现栈
class Node(object):
    def __init__(self, item):
        self.item = item
        self.next = None


class SingleListStack(object):
    def __init__(self):
        self.head = None

    def is_empty(self):
        return self.head is None

    def push(self, item):
        node = Node(item)
        if self.is_empty():
            self.head = node
        else:
            cur = self.head
            while cur.next:
                cur = cur.next
            cur.next = node

    def pop(self):
        if not self.is_empty():
            cur = self.head
            prev = cur
            if self.size() == 1:
                self.head = None
                return cur.item
            while cur.next:
                prev, cur = cur, cur.next
            prev.next = None
            return cur.item

    def peek(self):
        if not self.is_empty():
            cur = self.head
            while cur.next:
                cur = cur.next
            return cur.item

    def size(self):
        count = 0
        cur = self.head
        while cur:
            count += 1
            cur = cur.next
        return count

栈的基本操作性能：
入栈：时间复杂为O(1)
出栈：时间复杂为O(1)

队列

什么是队列： 队列是一种线性数据结构，元素只能队尾进去，队头出去。队列中取出元素的规律：先进先出。同样的，队列的实现可以通过数组或链表。

队列的基本操作和代码实现：

# 通过顺序表来实现
class ArrayQueue(object):
    def __init__(self):
        self.items = []

    def enqueue(self, item):
        """从队尾入队"""
        self.items.append(item)

    def dequeue(self):
        """从队头出队"""
        return self.items.pop(0)

    def is_empty(self):
        """判断队列是否为空"""
        return self.items == []

    def size(self):
        """队列的元素个数"""
        return len(self.items)


# 通过链表来实现
class Node(object):
    def __init__(self, item):
        self.item = item
        self.next = None


class SingleListQueue(object):
    def __init__(self):
        self.head = None

    def enqueue(self, item):
        node = Node(item)
        if self.is_empty():
            self.head = node
        else:
            cur = self.head
            while cur.next:
                cur = cur.next
            cur.next = node

    def dequeue(self):
        if not self.is_empty():
            item = self.head.item
            self.head = self.head.next
            return item

    def is_empty(self):
        return self.head is None

    def size(self):
        count = 0
        cur = self.head
        while cur:
            count += 1
            cur = cur.next
        return count

队列的基本操作性能：
基于数组实现：
入队：时间复杂度为O(1);
出队：时间复杂度为O(n)

基于链表实现：
入队：时间复杂度为O(n);
出队：时间复杂度为O(1)

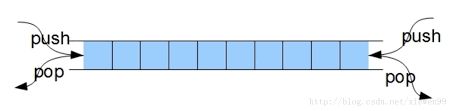
双端队列

集合了栈和队列的特点，既可先入先出，也可后入先出。

栈和队列的应用

栈的应用：逆流而上回溯历史

• 实现递归的逻辑，栈可以回溯方法的调用链
• 面包屑导航：用户浏览页面的时候，可以回溯到上一级或上上一级

队列的应用：历史的顺序回放

• 多线程任务队列，按入队顺序处理

散列表（哈希表）

什么是散列表： 散列表的数据结构提供了键(key)与值(value)的映射关系 ，根据给定的key可以高效查出对应的value,时间复杂度接近O(1)。散列表可以说是数组和链表的结合。

散列表的实现原理： 散列表在本质上也是一个数组，我们需要一个“中转站“（哈希函数），通过某种方式把key和数组下标进行转换。即key经过哈希函数转成对应的数组下标。

哈希冲突： 随着数据的不断增加，不同的key通过哈希函数获得的下标有可能是相同的，这就是哈希冲突。解决哈希冲突的方式有链表法：即数组的元素是链表头节点，当发生哈希冲突时，通过头节点的next指针指向下一个元素节点，当查询时，先根据key找到对应的下标元素（链表头节点），再遍历该链表，判断key是否相同，最后返回该key对应的value值。

扩容： 当散列表达到一定饱和度时，key映射位置发生冲突的概率会逐渐提高，对后续查询和插入的性能有很大的影响，这时需要扩容：创建一个2倍长度的空数组，遍历源数组，把原数组的元素重新hash到新的数组上。重新哈希的原因有： 一是数组长度变化，影响哈希规则，二是可以尽可能在新数组中分配均匀。

树的介绍

什么是树： 是一种抽象数据类型（ADT）或是实作这种抽象数据类型的数据结构，用来模拟具有树状结构性质的数据集合。它是由n（n>=1）个有限节点组成一个具有层次关系的集合。

树的特点：

• 每个节点有零个或多个子节点；
• 没有父节点的节点称为根节点；
• 每一个非根节点有且只有一个父节点；
• 除了根节点外，每个子节点可以分为多个不相交的子树。
  

二叉树

什么是二叉树

二叉树： 这种树的每个节点最多只有2个孩子节点。

完全二叉树：

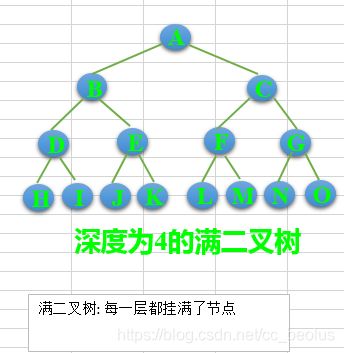
满二叉树：

二叉树的存储实现：
1.链式存储结构： 每个节点包括3部分：存储数据的data变量，指向左孩子的left指针，指向右孩子的right指针。

class Node(object):
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None


class BinaryTree(object):
    def __init__(self):
        self.root = None
        
    def add(self, data):
        """添加节点"""

2.数组： 使用数组存储时，会按照层级顺序把二叉树的节点放到数组中对应的位置上。如果某一个节点的左孩子或右孩子空缺，则数组的相应位置也空出来。

假如某个父节点的下标为parent, 那么它的左孩子下标为：2 * parent + 1，右孩子的下标为：2 * parent + 2.

二叉树的应用

主要应用： 用于查找操作和维持相对顺序。

二叉查找树：

• 如果左子树不为空，则左子树上所有节点的值都小于根节点的值；
• 如果右子树不为空，则右子树上所有节点的值都大于根节点的值；
• 左、右子树也都是二叉查找树。

对于一个节点分布相对均衡的二叉查找树来说，查询节点的时间复杂度为O(logn).

维持相对顺序： 对于二叉查找树，新插入的节点，需遵循二叉查找树的特点，插入到合适的位置上。可能会出现左子树的节点比右子树的节点多得多，这就是节点分布不均衡，导致查询节点复杂度退化为O(n)了，这需要二叉树的自平衡，如红黑树、AVL树等。

二叉树的遍历

深度优先遍历：

• 前序遍历：根节点–>左节点–>右节点
• 中序遍历：左节点–>根节点–>右节点
• 后序遍历：左节点–>右节点–>根节点

广度优先遍历：

• 层序遍历：由上至下，由左往右。

两种遍历的代码实现：

class Node(object):
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None


# 递归版本
class BinaryTree1(object):
    def __init__(self):
        self.root = None

    def add(self, data):
        """添加节点"""

    def preorder(self, root):
        """前序遍历"""
        if root is None:
            return
        print(root.data)
        self.preorder(root.left)
        self.preorder(root.right)

    def inorder(self, root):
        """中序遍历"""
        if root is None:
            return
        self.inorder(root.left)
        print(root.data)
        self.inorder(root.right)

    def postorder(self, root):
        """后序遍历"""
        if root is None:
            return
        self.postorder(root.left)
        self.postorder(root.right)
        print(root.data)

    def breadth_travel(self):
        """利用队列实现树的层次遍历"""
        if self.root is None:
            return
        queue = [self.root]
        while queue:
            node = queue.pop(0)
            if node.left:
                queue.append(node.left)
            if node.right:
                queue.append(node.right)
            print(node.data)


# 通过栈回调
class BinaryTree2(object):
    def __init__(self):
        self.root = None

    def add(self, data):
        """添加节点"""
        node = Node(data)
        # 如果树是空的，则对根节点赋值
        if self.root is None:
            self.root = node
        else:
            queue = []
            queue.append(self.root)
            # 对已有的节点进行层次遍历
            while queue:
                # 弹出队列的第一个元素
                cur = queue.pop(0)
                if cur.left is None:
                    cur.left = node
                    return
                elif cur.right is None:
                    cur.right = node
                    return
                else:
                    # 如果左右子树都不为空，加入队列继续判断
                    queue.append(cur.left)
                    queue.append(cur.right)

    def preorder(self, root):
        """前序遍历"""
        # ArrayStack，在栈介绍那里已经实现
        stack = ArrayStack()
        while root is not None or not stack.is_empty():
            while root is not None:
                print(root.data)
                stack.push(root)
                root = root.left

            # 如果该节点没有左孩子，则弹出栈顶节点，访问该节点右孩子
            if not stack.is_empty():
                root = stack.pop()
                root = root.right

    def inorder(self, root):
        """中序遍历"""
        stack = ArrayStack()
        while root is not None or not stack.is_empty():
            while root is not None:
                stack.push(root)
                root = root.left
            # 如果该节点没有左孩子，则弹出栈顶节点，访问该节点右孩子
            if not stack.is_empty():
                root = stack.pop()
                print(root.data)
                root = root.right

    def postorder(self, root):
        """后序遍历"""
        stack = ArrayStack()
        prev = None
        while root is not None or not stack.is_empty():
            while root is not None:
                stack.push(root)
                root = root.left

            if not stack.is_empty():
                root = stack.pop()
                if not root.right or root.right == prev:
                    print(root.data)
                    prev = root
                    root = None
                else:
                    stack.push(root)
                    root = root.right

    def breadth_travel(self):
        """利用队列实现树的层次遍历"""
        if self.root is None:
            return
        queue = [self.root]
        while queue:
            node = queue.pop(0)
            if node.left:
                queue.append(node.left)
            if node.right:
                queue.append(node.right)
            print(node.data)

二叉堆

什么是二叉堆： 二叉堆本质上是一种完全二叉树，它分为最大堆和最小堆两种类型。二叉堆的根节点叫作堆顶。

什么是最大堆、最小堆： 最大堆的任何一个父节点的值都大于或者等于它左、右孩子节点的值。反之，是最小堆。

二叉堆的自我调整： 指的是把一个不符合堆性质的完全二叉树，调整成一个堆。插入新节点、删除节点、构建二叉堆都会进行堆的自我调整。

• 插入节点：插入的位置是二叉树的最后一个位置。新节点通过与父节点比较，不断‘上浮’，直到整颗树都调整完成。
• 删除节点：被删除的节点是处于堆顶的节点。调整过程：把最后一个位置的节点临时补位到堆顶位置，然后通过与左、右孩子比较，不断‘下沉’，直到整颗树都调整完成。
• 构建二叉堆：把一个无序的完全二叉树调整为二叉堆，本质就是让所有的非叶子节点依次‘下沉’。调整过程：从最后一个非叶子节点开始调整，不断的比较和‘下沉’，最后调整堆顶节点。

各操作的时间复杂度： 插入和删除操作，时间复杂度为O(logn)， 构建二叉树时间复杂度为O(n)。

二叉堆的代码实现： 二叉堆的存储方式是顺序存储，即所有的节点都是存储在数组中。假如父节点的下标是parent,则左孩子的下标为2parent+1, 右孩子的下标为2parent+2.

class BinaryHeap:
	"""最小堆的实现"""
	
    def __init__(self):
        self.heap = []

    def up_adjust(self):
        """上浮调整。插入新节点"""
        # 如果最后一个节点是左孩子，则parent_idx = (child_idx -1) // 2
        # 如果最后一个节点是右孩子，则parent_idx = (child_idx -2) // 2, 而右孩子
        # 的下标一定是偶数，则有(child_idx -2) // 2 = (child_idx -1) // 2
        child_idx = len(self.heap) - 1
        parent_idx = (child_idx - 1) // 2

        # temp用于保存插入的叶子节点，用于最后的赋值
        temp = self.heap[child_idx]

        while child_idx > 0 and temp < self.heap[parent_idx]:
            self.heap[child_idx] = self.heap[parent_idx]
            child_idx = parent_idx
            parent_idx = (parent_idx - 1) // 2
            self.heap[child_idx] = temp

    def down_adjust(self, parent_idx):
        """下沉调整。删除节点"""
        # 保存父节点的值，用于最后的赋值
        temp = self.heap[parent_idx]
        child_idx = 2 * parent_idx + 1
        while child_idx < len(self.heap):
            # 如果有右孩子，且右孩子的值小于左孩子，则定位到右孩子
            if child_idx + 1 < len(self.heap) and self.heap[child_idx+1] < self.heap[child_idx]:
                child_idx += 1
            # 如果父节点小于任何一个孩子的值，则直接退出循环, 无需调整
            if self.heap[parent_idx] < self.heap[child_idx]:
                break
            self.heap[parent_idx] = self.heap[child_idx]
            parent_idx = child_idx
            child_idx = child_idx * 2 + 1
            self.heap[parent_idx] = temp

    def build_heap(self):
        """构建堆"""
        # 从最后一个非叶子节点开始，依次做下沉调整
        for i in range((len(self.heap)-2)//2, -1, -1):
            self.down_adjust(i)


if __name__ == '__main__':
    h = BinaryHeap()
    h.heap = [1, 3, 2, 6, 5, 6, 8, 9, 10, 0]
    h.up_adjust()
    print(h.heap)
    h.heap = [7, 1, 3, 10, 5, 2, 8, 9, 6]
    h.build_heap()
    print(h.heap)

二叉堆的作用： 实现堆排序和优先队列。

优先队列

最大优先队列： 无论入队顺序如何，都是当前最大的元素优先出队；
最小优先队列： 无论入队顺序如何，都是当前最小的元素优先出队。

优先队列的实现： 最大堆/最小堆。入队就是堆的插入操作，出队就是堆顶节点的删除操作。

class PriorityQueue:
    """最小优先队列"""

    def __init__(self):
        self.queue = []

    def up_adjust(self):
        """上浮调整。插入新节点"""
        # 如果最后一个节点是左孩子，则parent_idx = (child_idx -1) // 2
        # 如果最后一个节点是右孩子，则parent_idx = (child_idx -2) // 2, 而右孩子
        # 的下标一定是偶数，则有(child_idx -2) // 2 = (child_idx -1) // 2
        child_idx = len(self.queue) - 1
        parent_idx = (child_idx - 1) // 2

        # temp用于保存插入的叶子节点，用于最后的赋值
        temp = self.queue[child_idx]

        while child_idx > 0 and temp < self.queue[parent_idx]:
            self.queue[child_idx] = self.queue[parent_idx]
            child_idx = parent_idx
            parent_idx = (parent_idx - 1) // 2
            self.queue[child_idx] = temp

    def down_adjust(self, parent_idx=0):
        """下沉调整。删除节点"""
        # 保存父节点的值，用于最后的赋值
        temp = self.queue[parent_idx]
        child_idx = 2 * parent_idx + 1
        while child_idx < len(self.queue):
            # 如果有右孩子，且右孩子的值小于左孩子，则定位到右孩子
            if child_idx + 1 < len(self.queue) and self.queue[child_idx+1] < self.queue[child_idx]:
                child_idx += 1
            # 如果父节点小于任何一个孩子的值，则直接退出循环, 无需调整
            if self.queue[parent_idx] < self.queue[child_idx]:
                break
            self.queue[parent_idx] = self.queue[child_idx]
            parent_idx = child_idx
            child_idx = child_idx * 2 + 1
            self.queue[parent_idx] = temp

    def enqueue(self, item):
        self.queue.append(item)
        self.up_adjust()

    def dequeue(self):
        if len(self.queue) == 0:
            return
        if len(self.queue) == 1:
            return self.queue.pop()
        head = self.queue[0]
        self.queue[0] = self.queue.pop()
        self.down_adjust()
        return head


if __name__ == '__main__':
    q = PriorityQueue()
    q.enqueue(1)
    q.enqueue(3)
    q.enqueue(5)
    q.enqueue(0)
    q.enqueue(4)
    q.enqueue(2)
    q.enqueue(8)
    q.enqueue(7)

    print([q.dequeue() for i in range(8)])

python常见数据类型的底层实现原理

list类型的底层实现

tuple类型的底层实现

dict类型的底层实现

set类型的底层实现