二叉树面试算法合集
1. 二叉树的定义
class TreeNode{
int val;
TreeNode left;
TreeNode right;
}
2. 二叉树常用算法模板
// 1.递归序二叉树
TreeNode dfs(TreeNode root){
if(root==null){
return null;
}
// sout(root.val) 在这打印，先序遍历
dfs(root.left);
// sout(root.val) 在这打印，中序遍历
dfs(root.right);
// sout(root.val) 在这打印，后序遍历
}
// 2.非递归序 : 用栈模拟递归压栈操作，所有二叉树都可以被分解为左边界/右边界，如中序遍历非递归的本质其实是：将左根右的右换成下一个左根右
2.1 弹出节点，并打印
2.2 先压栈右，后压左（先序遍历），
//3.宽续遍历： 队列
public List<List<Integer>> levelOrder(TreeNode root) {
Queue<TreeNode> queue=new LinkedList();
List<List<Integer>> ans=new ArrayList();
if(root==null)return ans;
queue.add(root);
while(!queue.isEmpty()){
int all=queue.size();
List<Integer> res=new ArrayList();
for(int i=0;i<all;i++){
TreeNode t=queue.poll();
if(t.left!=null)queue.add(t.left);
if(t.right!=null)queue.add(t.right);
res.add(t.val);
}
ans.add(res);
}
return ans;
}
3. 二叉树常用数据结构
- 哈希表（map），记录节点的指向
4. 例题
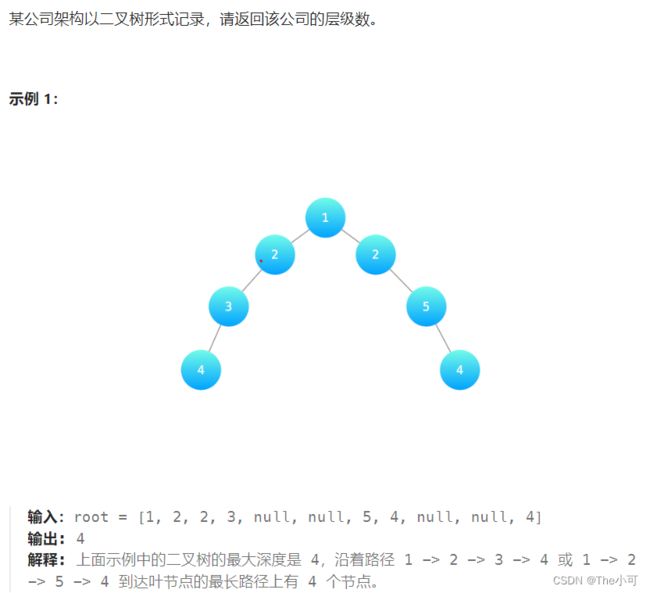
4.1 二叉树的最大深度
- leetcode 原题 : 二叉树的最大深度
int maxDepth(TreeNode root) {
if(root==null){
return 0;
}
return max(maxDepth(root->left),maxDepth(root->right))+1;
}
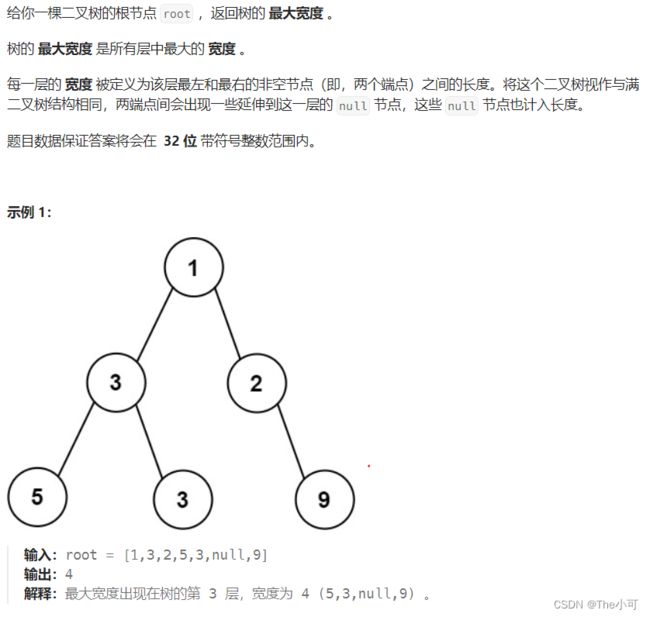
4.2 二叉树的最大宽度
核心思想 : 利用map来统计某一层的信息（计数，记录第一个或最后一个）
- 二叉树的最大宽度（同层一共有多少节点）
//map记录第几层有几个节点，n为当前节点在第几层
HashMap<Integer,Integer> map=new HashMap()
int maxWidth(TreeNode){
dfs(TreeNode,1);
int mx=0;
for(int level : map.keySet()){
mx=Math.max(mx,map.get(level));
}
return mx;
}
void dfs(TreeNode root,int n){
if(root==null){
return;
}
map.put(n,map.getOrDefault(n,0)+1);
f(root.left,map,n+1);
f(root.right,map,n+1);
}
- leetcode 原题 : 二叉树的最大宽度（同层两非空节点的最远距离，包括空节点））
HashMap<Integer,Integer> map=new HashMap()
int width=0;
int maxWidth(TreeNode){
dfs(TreeNode,1,1);
return width;
}
void dfs(TreeNode root,int n,int val){
if(root==null){
return
}
map.putIfAbsent(n,val);
return Math.max(val-map.get(n)-1,Math.max(dfs(root.left,n+1,val*2),dfs(root.right,n+1,val*2+1)));
}
- leetcode 原题 : 二叉树的右视图（同层两非空节点的最远距离，包括空节点））
class Solution {
int mx=0;
List<Integer> list = new ArrayList();
Map<Integer,Integer> map = new HashMap();
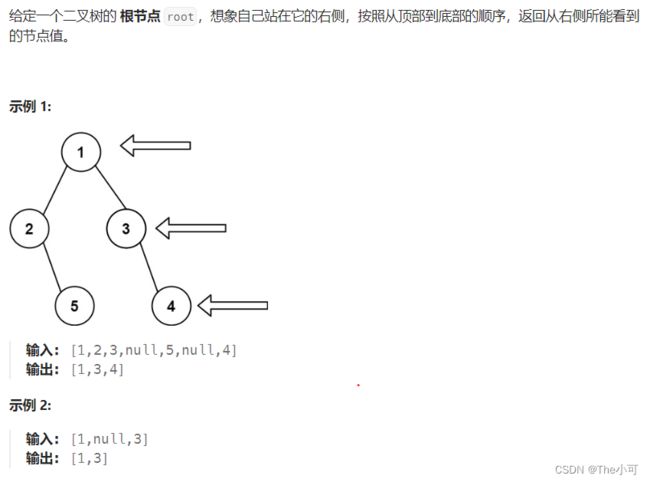
public List<Integer> rightSideView(TreeNode root) {
dfs(root , 0);
for(int i=0;i<mx;i++){
list.add(map.get(i));
}
return list;
}
void dfs(TreeNode node , int height){
if(node==null){
mx=Math.max(mx,height);
return;
}
map.put(height,node.val);
dfs(node.left,height+1);
dfs(node.right,height+1);
}
}
4.3 二叉树倒数第n个节点
TreeNode node=null;
int n;
TreeNode getN(TreeNode head , int n){
this.n=n;
dfs(head);
return node;
}
void dfs(TreeNode head){
if(head==null){
return;
}
dfs(head.right,n);
n--;
if(n==0){
node=head;
return;
}
dfs(head.left,n);
}
- leetcode 原题 : 二叉搜索树中第K小的元素
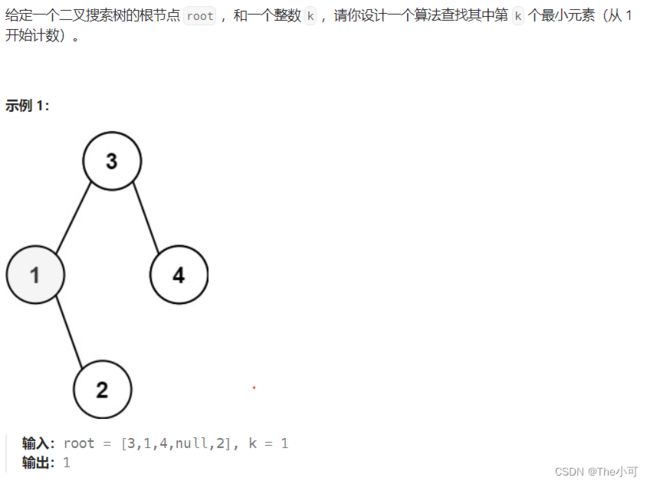
class Solution {
int k;
int ans=-1;
public int kthSmallest(TreeNode root, int k) {
this.k=k;
dfs(root);
return ans;
}
void dfs(TreeNode root){
if(root==null)return;
dfs(root.left);
k--;
if(k==0){
ans=root.val;
}
dfs(root.right);
}
}
递归核心思想 : 能否转化为子问题（和子问题的解决逻辑一致） + 当前节点需要满足的条件
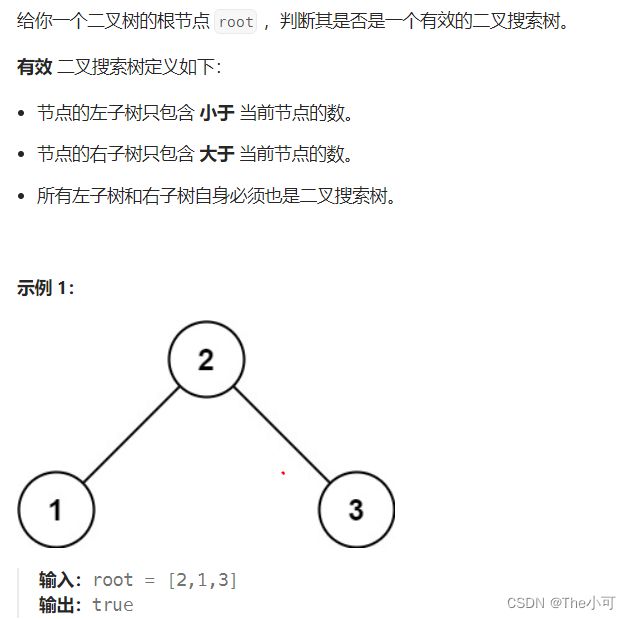
4.4 判断一棵树是否是搜索二叉树
-
leetcode 原题 : 判断一棵树是否是搜索二叉树
-
转化为递归逻辑 : 左孩子是二叉搜索树 + 右孩子是二叉搜索树 + 左节点的值<当前节点的值<右节点的值
boolean isBST(TreeNode root){
return isBST(root,Integer.MIN_VALUE,Integer.MAX_VALUE);
}
// [n,m] 为当前节点的上下界，然后以此节点继续缩小区间
boolean isBST(TreeNode root,int n,int m){
if(root==null){
return true;
}
return root.val>n && root.val<m && isBST(root.left,n,root.val) && isBST(root.right,root.val,m);
}
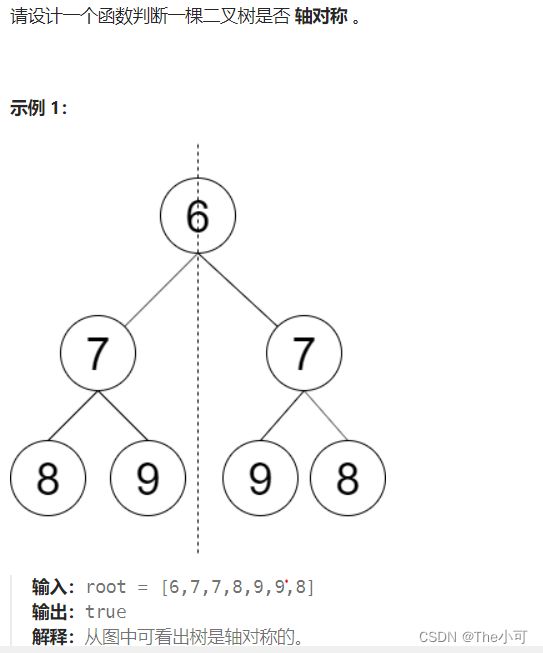
4.5 判断对称二叉树
-
leetcode 原题 : 判断对称二叉树
-
转化为递归逻辑 : 左孩子的左子树=右孩子的右子树 + 左孩子的右子树=右孩子的左子树+ 左节点的值 = 右节点的值
bool isSymmetric(TreeNode root) {
return check(root,root);
}
bool check(TreeNode l,TreeNode r){
if(l==null && r==null) return true;
if(l==null || r==null) return false;
return l.val == r.val && check(l.left,r.right) && check(l.right,r.left);
}
4.6 判断一棵树是否是完全二叉树 (宽续遍历)
- 无法转化为子问题，因为字节满足完全二叉树与父节点没有关系
Boolean isCBT(TreeNode head){
if(head==null){
return true;
}
LinkedList<TreeNode> queue=new LinkedList();
queue.add(head);
boolean single=false;
while(!queue.isEmpty()){
TreeNode cur=queue.poll();
//3.2 遇到第一个只存在一个子节点的，之后的全部节点都要为叶子节点
if(single && !(cur.left==null && cur.right==null)){
return false;
}
//3.1 遇到有右节点而无左节点直接返回false
if(left==null && right!=null){
return false
}
if(cur.left!=null){
queue.add(cur.left);
}
if(cur.right!=null){
queue.add(cur.right);
}
if(cur.right==null || cur.left==null){
single=true;
}
}
}
4.7 判断一棵树是否是满二叉树
- 转化为递归逻辑 : 左孩子是满二叉树 + 右孩子是满二叉树 + 当前节点的左孩子和右孩子要么都有要么都没有
//4.满二叉树的判断（1.左右节点要么都，要么都没有。2.左节点是满二叉树。3.右节点是满二叉树）
Boolean dfs(TreeNode root){
if(root==null){
return true;
}
if(root.left==null || root.right==null){
if(root.left==null && root.right==null){
return true;
}else{
return false
}
}else{
return ture;
}
return dfs(root.left) && dfs(root.right);
}
4.8 判断一棵树是否是平衡二叉树
-
leetcode 原题 : 判断一棵树是否是平衡二叉树
-
转化为递归逻辑 : 左孩子是平衡二叉树 + 右孩子是平衡二叉树 + 当前节点的左孩子与右孩子之前的高度差不能大于1
//5.判断是否是平衡二叉树（1.左右节点高度相差<=1 2.左节点是平衡二叉树。3.右节点是平衡二叉树。）
Boolean BT(TreeNode root){
if(root==null){
return true;
}
return Math.abs(maxHeight(root.left)-maxHeight(root.right))<=1 && BT(root.left) && BT(root.right);
}
int maxHeight(root){
if(root==null){
return 0;
}
return Math.max(maxHeight(root.left),maxHeight(root.right))+1;
}
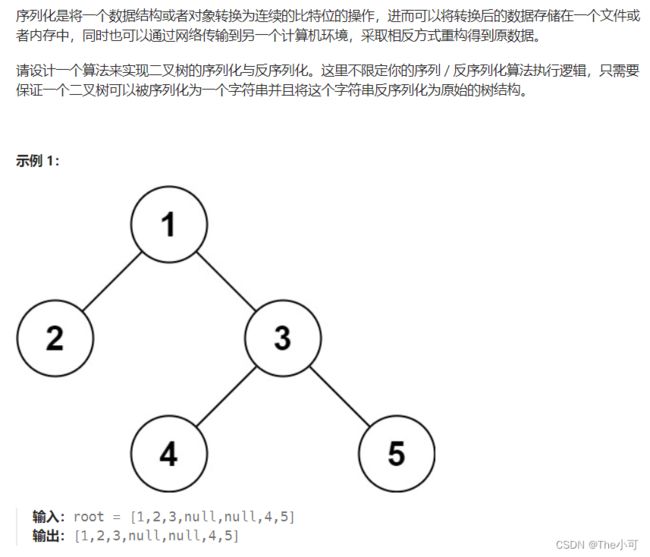
4.9 二叉树的序列化和反序列化
-
leetcode 原题 : 二叉树的序列化和反序列化
-
转化为递归逻辑 : 当前节点序列化 + 左孩子序列化+ 右孩子序列化
//7.二叉树的序列化和反序列化
string serialize(TreeNode root){
if(root==null){
return "null"
}
return root.val + "," + serizable(root.left) + "," + serizable(root.right);
}
TreeNode deserialize(String s){
return deserialize(new ArrayList<String>(Arrays.asList(data.split(','))));
}
TreeNode deserialize(ArrayList<string> list){
if("null".equals(list.get(0))){
list.remove(0);
return null;
}
TreeNode root=new TreeNode(Integer.parseInteger(list.get(0)));
list.remove(0)
root.left=deserialize(list);
root.right=deserialize(list);
return root;
}
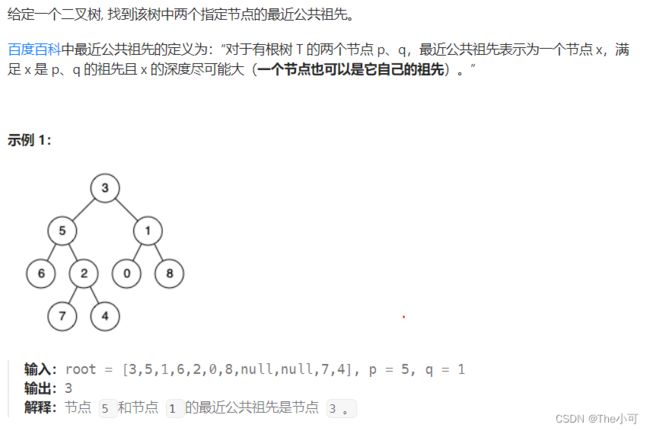
4.10 给定两个节点a，b，找到他们的最近公共祖先
- leetcode 原题 : 最近公共祖先
//6.给定两个节点a，b，找到他们的最低公共祖先
TreeNode find（TreeNode root,TreeNode a,TreeNode b）{
if(root==null || a==root || b==root){
return root;
}
// 看子节点是不是a或b节点的公共祖先
TreeNode left=find(root.left,a,b);
TreeNode right=find(root.right,a,b);
// 除非a，b节点至少有一个不在树里面，才两个都为空
if(left==null && right==null){
return null;
}
// a，b都在其中一个子节点里
if(left==null || right==null){
return left==null ? right : left；
}
// a,b在两个子节点个占一个
return root;
}
4.11 求根节点到叶节点数字之和
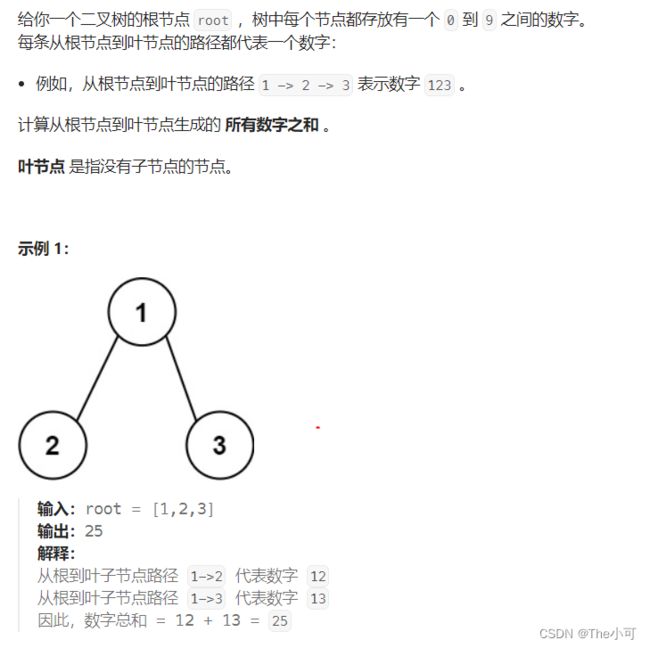
- leetcode 原题 : 求根节点到叶节点数字之和
class Solution {
public int sumNumbers(TreeNode root) {
return dfs(root,0);
}
int dfs(TreeNode root , int s){
if(root==null){
return 0;
}
if(root.left==null && root.right==null){
return s*10+root.val;
}
return dfs(root.left,s*10+root.val) + dfs(root.right,s*10+root.val);
}
}
4.12 二叉树中的最大路径和
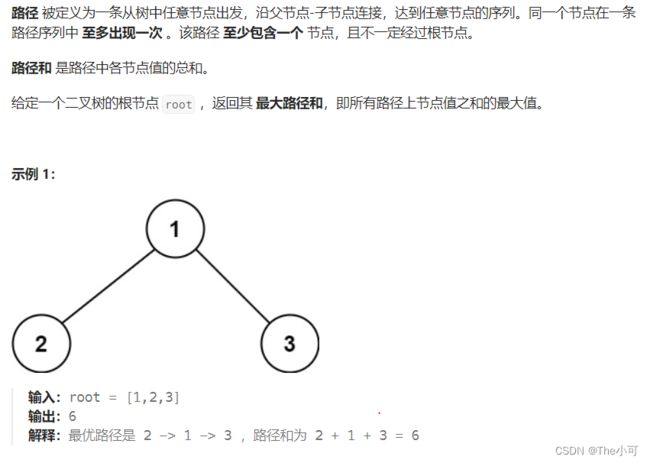
- leetcode 原题 : 二叉树中的最大路径和
int mx=Integer.MIN_VALUE;
public int maxPathSum(TreeNode root) {
dfs(root);
return mx;
}
int dfs(TreeNode root){
if(root==null){
return 0;
}
int left=Math.max(0,dfs(root.left));
int right=Math.max(0,dfs(root.right));
mx=Math.max(mx,left+right+root.val);
return root.val+Math.max(right,left);
}
4.13 实现 Trie (前缀树)
- leetcode 原题 : 前缀树
class Trie {
private Trie[] children;
private boolean end;
public Trie() {
this.children=new Trie[26];
end=false;
}
public void insert(String word) {
Trie root=this;
for(char ch : word.toCharArray()){
int index=ch-'a';
if(root.children[index]==null){
root.children[index]=new Trie();
}
root=root.children[index];
}
root.end=true;
}
public boolean search(String word) {
Trie root=isPre(word);
return root!=null && root.end;
}
public boolean startsWith(String prefix) {
return isPre(prefix)!=null;
}
public Trie isPre(String s){
Trie root=this;
for(char ch : s.toCharArray()){
int index= ch-'a';
if(root.children[index]==null){
return null;
}
root=root.children[index];
}
return root;
}
}
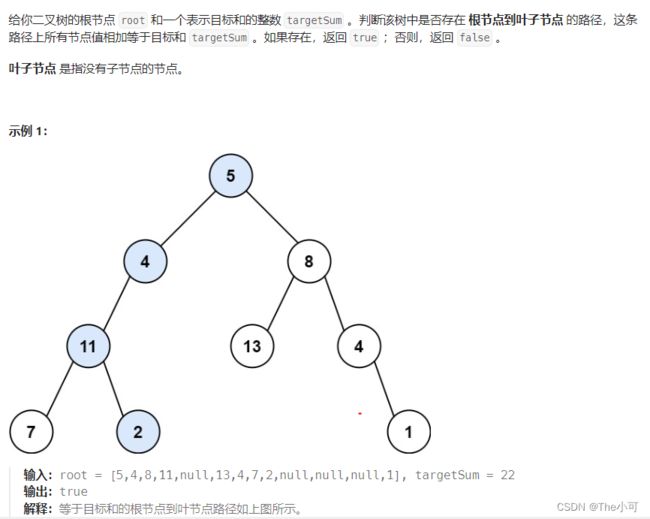
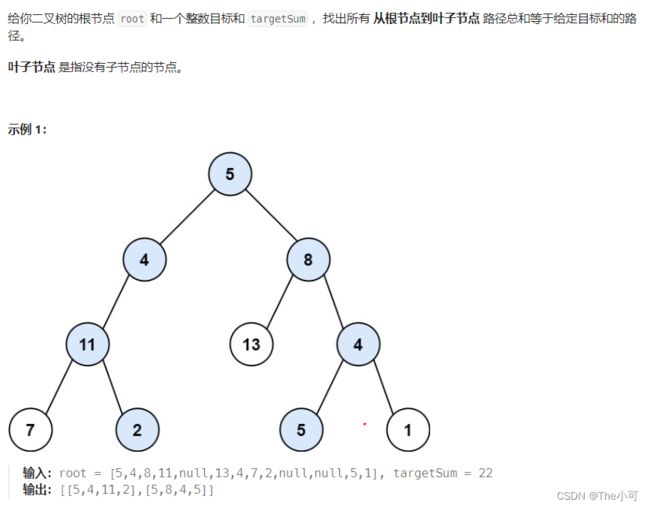
4.14 路径总和
-
leetcode 原题 : 路径总和
-
核心思想 : 一直向下找 target - root.val 的值
public boolean hasPathSum(TreeNode root, int targetSum) {
if(root==null) return false;
if(root.left==null && root.right==null){
return root.val == targetSum;
}
return hasPathSum(root.left,targetSum-root.val) || hasPathSum(root.right,targetSum-root.val);
}
-
leetcode 原题 : 路径总和II
-
核心思想 : 向上回溯时（走到底）删除当前元素
class Solution {
List<List<Integer>> sum = new ArrayList<List<Integer>>();
List<Integer> list=new ArrayList<Integer>();
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
dfs(root,targetSum);
return sum;
}
public void dfs(TreeNode node,int targetSum){
if(node == null) return;
if(node.left==null && node.right==null){
if(targetSum==node.val){
List t= new ArrayList<Integer>(list);
t.add(node.val);
sum.add(t);
}
}
list.add(node.val);
dfs(node.left,targetSum-node.val);
dfs(node.right,targetSum-node.val);
list.remove(list.size()-1);
}
}
4.15 打家劫舍 III
-
leetcode 原题 : 打家劫舍 III
-
树形DP核心思想 : 每个节点都返回选（左右孩子都不选）与不选（左孩子选与不选的最大值，右孩子选与不选的最大值）对应的最大价值
public int rob(TreeNode root) {
int[] ans=dfs(root);
return Math.max(ans[0],ans[1]);
}
int[] dfs(TreeNode root){
if(root==null){
return new int[]{0,0};
}
int[] left=dfs(root.left);
int[] right=dfs(root.right);
int select=left[1]+right[1]+root.val;
int noselect=Math.max(left[0],left[1])+Math.max(right[0],right[1]);
return new int[]{select,noselect};
}
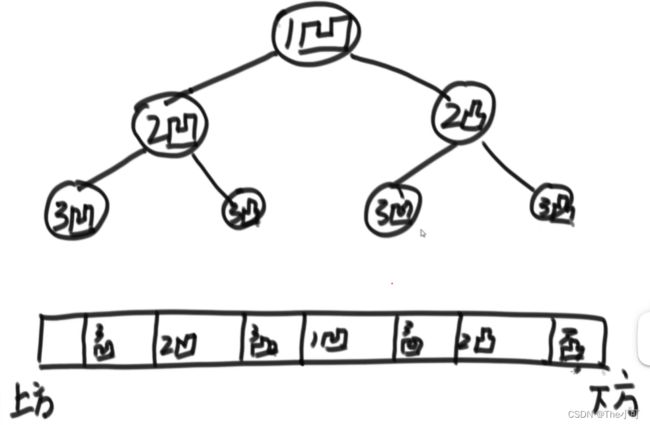
经典折痕问题（将一个长纸条按一个方向折，第一次是凹折痕（折痕顺序是 : 1凹），第二次是凹凹凸折痕（折痕顺序是 : 2凹，1凹，2凸）。给你一个折的次数，返回折后的凹凸次序）
//本质 : 将折痕的上下两端模拟成二叉树的左右两端，左子树都是凹，右子树都是凸的.最后取中序遍历
void printAllFolds(int n){
printAllFolds(0, n,true);
}
void printAllFolds(int i,int n,boolean down){
if(i>n){
return;
}
printAllFolds(i+1,n,true);
sout(down ? "凹" : "凸");
printAllFolds(i+1,n,false);
}
算法合集持续更新中！下一篇 堆
