【编程之路】面试必刷TOP101：二叉树系列（37-41，Python实现）

【面试必刷TOP101】系列包含：

• 面试必刷TOP101：链表（01-05，Python实现）
• 面试必刷TOP101：链表（06-10，Python实现）
• 面试必刷TOP101：链表（11-16，Python实现）
• 面试必刷TOP101：二分查找/排序（17-22，Python实现）
• 面试必刷TOP101：二叉树系列（23-30，Python实现）
• 面试必刷TOP101：二叉树系列（31-36，Python实现）
• 面试必刷TOP101：二叉树系列（37-41，Python实现）
• 面试必刷TOP101：堆、栈、队列（42-49，Python实现）
• 面试必刷TOP101：哈希表（50-54，Python实现）
• 面试必刷TOP101：递归 / 回溯（55-61，Python实现）
• 面试必刷TOP101：动态规划（入门）（62-66，Python实现）
• 面试必刷TOP101：动态规划（67-71，Python实现）
• 面试必刷TOP101：动态规划（72-77，Python实现）
• 面试必刷TOP101：动态规划（78-82，Python实现）
• 面试必刷TOP101：字符串（83-86，Python实现）
• 面试必刷TOP101：双指针（87-94，Python实现）
• 面试必刷TOP101：贪心算法（95-96，Python实现）
• 面试必刷TOP101：模拟（97-99，Python实现）

---

37.二叉搜索树的最近公共祖先

• 小试牛刀

37.1 递归法

我们也可以利用二叉搜索树的性质：对于某一个节点若是p与q都小于等于这个这个节点值，说明p、q都在这个节点的左子树，而最近的公共祖先也一定在这个节点的左子树；若是p与q都大于等于这个节点，说明p、q都在这个节点的右子树，而最近的公共祖先也一定在这个节点的右子树。而若是对于某个节点，p与q的值一个大于等于节点值，一个小于等于节点值，说明它们分布在该节点的两边，而这个节点就是最近的公共祖先，因此从上到下的其他祖先都将这个两个节点放到同一子树，只有最近公共祖先会将它们放入不同的子树，每次进入一个子树又回到刚刚的问题，因此可以使用递归。

step 1：首先检查空节点，空树没有公共祖先。
step 2：对于某个节点，比较与p、q的大小，若p、q在该节点两边说明这就是最近公共祖先。
step 3：如果p、q都在该节点的左边，则递归进入左子树。
step 4：如果p、q都在该节点的右边，则递归进入右子树。

class Solution:
    def lowestCommonAncestor(self , root: TreeNode, p: int, q: int) -> int:
        if root is None:
            return -1
        if (p >= root.val and q <= root.val) or (p <= root.val and q >= root.val):
            return root.val
        elif p <= root.val and q <= root.val:
            return self.lowestCommonAncestor(root.left, p, q)
        else:
            return self.lowestCommonAncestor(root.right, p, q)

时间复杂度：O(n)，设二叉树共有 n 个节点，最坏情况递归遍历所有节点。
空间复杂度：O(n)，递归栈深度最坏为 n。

37.2 辅助栈

step 1：根据二叉搜索树的性质，从根节点开始查找目标节点，当前节点比目标小则进入右子树，当前节点比目标大则进入左子树，直到找到目标节点。这个过程成用数组记录遇到的元素。
step 2：分别在搜索二叉树中找到p和q两个点，并记录各自的路径为数组。
step 3：同时遍历两个数组，比较元素值，最后一个相等的元素就是最近的公共祖先。

class Solution:
    def getPath(self, root: TreeNode, p: int):
        path = []
        while p != root.val:
            path.append(root.val)
            if p < root.val:
                root = root.left
            else:
                root = root.right
        path.append(root.val)
        return path
        
    def lowestCommonAncestor(self , root: TreeNode, p: int, q: int) -> int:
        path1 = self.getPath(root, p)
        path2 = self.getPath(root, q)
        i = 0
        # 最后一个相同的节点就是最近公共祖先
        while i < len(path1) and i < len(path2):
            if path1[i] == path2[i]:
                res = path1[i]
                i = i + 1
            else:
                break
        return res

时间复杂度：$O(n)$，设二叉树共有 n 个节点，因此最坏情况二叉搜索树变成链表，搜索到目标节点需要 O(n)，比较路径前半段的相同也需要 O(n)。
空间复杂度：$O(n)$，记录路径的数组最长为 n。

38.在二叉树中找到两个节点的最近公共祖先

• 小试牛刀

38.1 深度优先搜索

既然要找到二叉树中两个节点的最近公共祖先，那我们可以考虑先找到两个节点全部祖先，可以得到从根节点到目标节点的路径，然后依次比较路径得出谁是最近的祖先。找到两个节点的所在可以深度优先搜索遍历二叉树所有节点进行查找。

step 1：利用dfs求得根节点到两个目标节点的路径：每次选择二叉树的一棵子树往下找，同时路径数组增加这个遍历的节点值。
step 2：一旦遍历到了叶子节点也没有，则回溯到父节点，寻找其他路径，回溯时要去掉数组中刚刚加入的元素。
step 3：然后遍历两条路径数组，依次比较元素值。
step 4：找到两条路径第一个不相同的节点即是最近公共祖先

class Solution:
    # 记录是否找到到达o的路径
    flag = False
    
    # 求根节点到目标节点的路径，不同于二叉搜索树
    def dfs(self, root: TreeNode, path: List[int], o: int):
        if root is None or self.flag:
            return
        path.append(root.val)
        if root.val == o:
            self.flag = True
            return
        # dfs遍历查找
        self.dfs(root.left, path, o)
        self.dfs(root.right, path, o)
        # 找到
        if self.flag:
            return
        # 该子树没有，回溯
        path.pop()
        
    def lowestCommonAncestor(self , root: TreeNode, o1: int, o2: int) -> int:
        path1 = []
        path2 = []
        # 求根节点到两个节点的路径
        self.dfs(root, path1, o1)
        # 重置flag，查找下一个
        self.flag = False
        self.dfs(root, path2, o2)
        i = 0
        # 最后一个相同的节点就是最近公共祖先
        while i < len(path1) and i < len(path2):
            if path1[i] == path2[i]:
                res = path1[i]
                i = i + 1
            else:
                break
        return res

时间复杂度：O(n)，其中 n 为二叉树节点数，递归遍历二叉树每一个节点求路径，后续又遍历路径。
空间复杂度：O(n)，最坏情况二叉树化为链表，深度为 n，递归栈深度和路径数组为 n。

38.2 递归

step 1：如果o1和o2中的任一个和root匹配，那么root就是最近公共祖先。
step 2：如果都不匹配，则分别递归左、右子树。
step 3：如果有一个节点出现在左子树，并且另一个节点出现在右子树，则root就是最近公共祖先.
step 4：如果两个节点都出现在左子树，则说明最低公共祖先在左子树中，否则在右子树。
step 5：继续递归左、右子树，直到遇到step1或者step3的情况。

class Solution:
    def lowestCommonAncestor(self , root: TreeNode, o1: int, o2: int) -> int:
        # 该子树没找到，返回-1
        if root is None:
            return -1
        # 该节点是其中某一个节点
        if o1 == root.val or o2 == root.val:
            return root.val
        # 左子树寻找公共祖先
        left = self.lowestCommonAncestor(root.left, o1, o2)
        # 右子树寻找公共祖先
        right = self.lowestCommonAncestor(root.right, o1, o2)
        # 左子树为没找到，则在右子树中
        if left == -1:
            return right
        # 右子树没找到，则在左子树中
        if right == -1:
            return left
        # 否则是当前节点
        return root.val

时间复杂度：O(n)，其中 n 为节点数，递归遍历二叉树每一个节点。
空间复杂度：O(n)，最坏情况二叉树化为链表，递归栈深度为 n。

39.序列化二叉树

• 小试牛刀

39.1 前序遍历

序列化即将二叉树的节点值取出，放入一个字符串中，我们可以按照前序遍历的思路，遍历二叉树每个节点，并将节点值存储在字符串中，我们用‘#’表示空节点，用‘!'表示节点与节点之间的分割。

反序列化即根据给定的字符串，将二叉树重建，因为字符串中的顺序是前序遍历，因此我们重建的时候也是前序遍历，即可还原。

step 1：优先处理序列化，首先空树直接返回“#”，然后调用SerializeFunction函数前序递归遍历二叉树。

SerializeFunction(root, res);

step 2：SerializeFunction函数负责前序递归，根据“根左右”的访问次序，优先访问根节点，遇到空节点在字符串中添加 ‘#’，遇到非空节点，添加相应节点数字和 ‘!’，然后依次递归进入左子树，右子树。

# 根节点
str.append(root.val).append('!');
# 左子树
SerializeFunction(root.left, str);
# 右子树
SerializeFunction(root.right, str);

step 3：创建全局变量 index 表示序列中的下标（C++中直接指针完成）。
step 4：再处理反序列化，读入字符串，如果字符串直接为 “#”，就是空树，否则还是调用DeserializeFunction函数前序递归建树。

TreeNode res = DeserializeFunction(str);

step 5：DeserializeFunction函数负责前序递归构建树，遇到‘#’则是空节点，遇到数字则根据感叹号分割，将字符串转换为数字后加入新创建的节点中，依据 “根左右”，创建完根节点，然后依次递归进入左子树、右子树创建新节点。

TreeNode root = new TreeNode(val);
......
# 反序列化与序列化一致，都是前序
root.left = DeserializeFunction(str); 
root.right = DeserializeFunction(str);

import sys
sys.setrecursionlimit(100000)
class Solution:
    def __init__(self):
        self.index = 0
        self.s = ""
    # 处理序列化
    def SerializeFunction(self, root):
        # 空节点
        if not root:
            self.s = self.s + '#'
            return
        # 根节点
        self.s = self.s + str(root.val) + '-'
        # 左子树
        self.SerializeFunction(root.left)
        # 右子树
        self.SerializeFunction(root.right)
        
    def Serialize(self, root):
        if not root:
            return '#'
        self.s = ""
        self.SerializeFunction(root)
        return self.s
    
    # 处理反序列化的功能函数
    def DeserializeFunction(self, s: str):
        # 到达叶节点时，构建完毕，返回继续构建父节点
        # 空节点
        if self.index >= len(s) or s[self.index] == '#':
            self.index = self.index + 1
            return None
        # 数字转换
        val = 0
        while s[self.index] != '-' and self.index != len(s):
            val = val * 10 + int(s[self.index])
            self.index = self.index + 1
        root = TreeNode(val)
        # 序列到底了，构建完成
        if self.index == len(s):
            return root
        else:
            self.index = self.index + 1
        root.left = self.DeserializeFunction(s)
        root.right = self.DeserializeFunction(s)
        return root
            
    def Deserialize(self, s):
        if s == '#':
            return None
        return self.DeserializeFunction(s)

时间复杂度：O(n)，其中n为二叉树节点数，前序遍历，每个节点遍历一遍。
空间复杂度：O(n)，最坏情况下，二叉树退化为链表，递归栈最大深度为n。

40.重建二叉树

• 小试牛刀

40.1 递归法

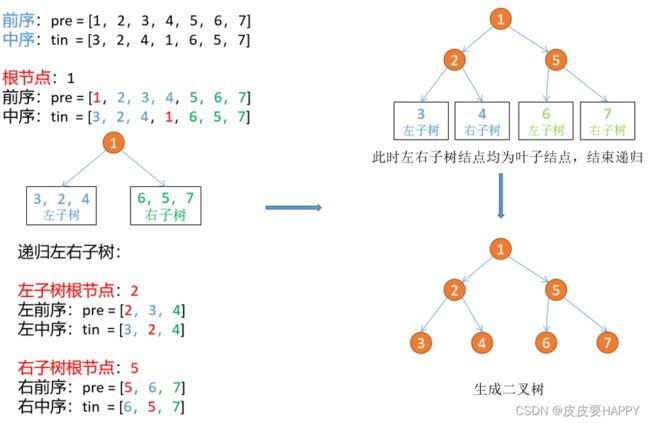
step 1：先根据前序遍历第一个点建立根节点。
step 2：然后遍历中序遍历找到根节点在数组中的位置。
step 3：再按照子树的节点数将两个遍历的序列分割成子数组，将子数组送入函数建立子树。
step 4：直到子树的序列长度为 0，结束递归。

class Solution:
    def reConstructBinaryTree(self , pre: List[int], vin: List[int]) -> TreeNode:
        n = len(pre)
        m = len(vin)
        if n == 0 or m == 0:
            return None
        root = TreeNode(pre[0])
        for i in range(len(vin)):
            if pre[0] == vin[i]:
                left_pre = pre[1:i+1]
                left_vin = vin[:i]
                root.left = self.reConstructBinaryTree(left_pre, left_vin)
                right_pre = pre[i+1:]
                right_vin = vin[i+1:]
                root.right = self.reConstructBinaryTree(right_pre, right_vin)
                break
        return root

时间复杂度：$O(n)$，其中 n 为数组长度，即二叉树的节点数，构建每个节点进一次递归，递归中所有的循环加起来一共 n 次。
空间复杂度：$O(n)$，递归栈最大深度不超过 n，辅助数组长度也不超过 n，重建的二叉树空间属于必要空间，不属于辅助空间。

40.2 辅助栈

借助栈来解决问题需要关注一个问题，就是前序遍历挨着的两个值比如m和n，它们会有下面两种情况之一的关系。
1、n是m左子树节点的值。
2、n是m右子树节点的值或者是m某个祖先节点的右节点的值。
对于第一种情况很容易理解，如果m的左子树不为空，那么n就是m左子树节点的值。
对于第二种情况，如果一个结点没有左子树只有右子树，那么n就是m右子树节点的值，如果一个结点既没有左子树也没有右子树，那么n就是m某个祖先节点的右节点，只要找到这个祖先节点就可以。

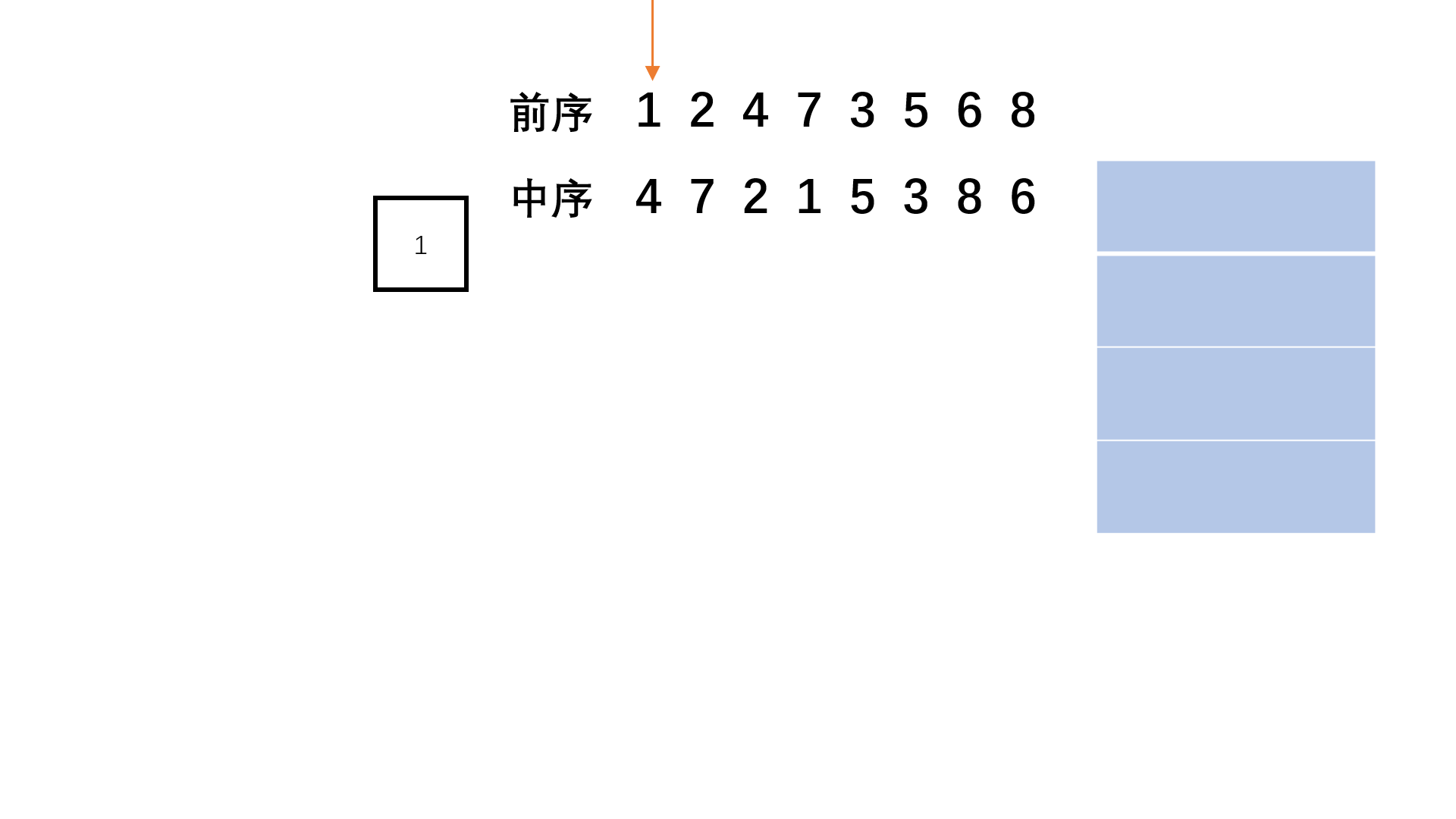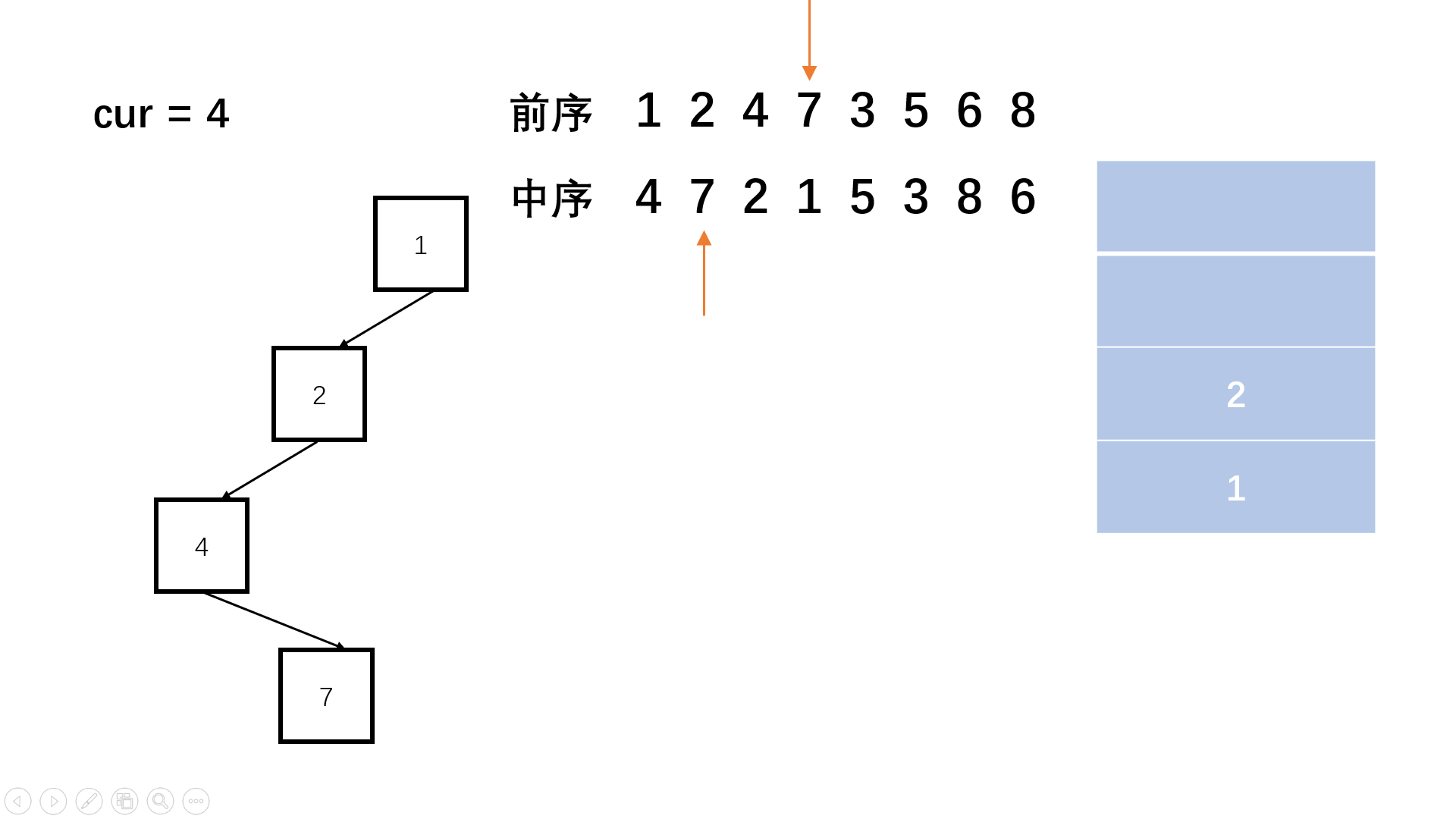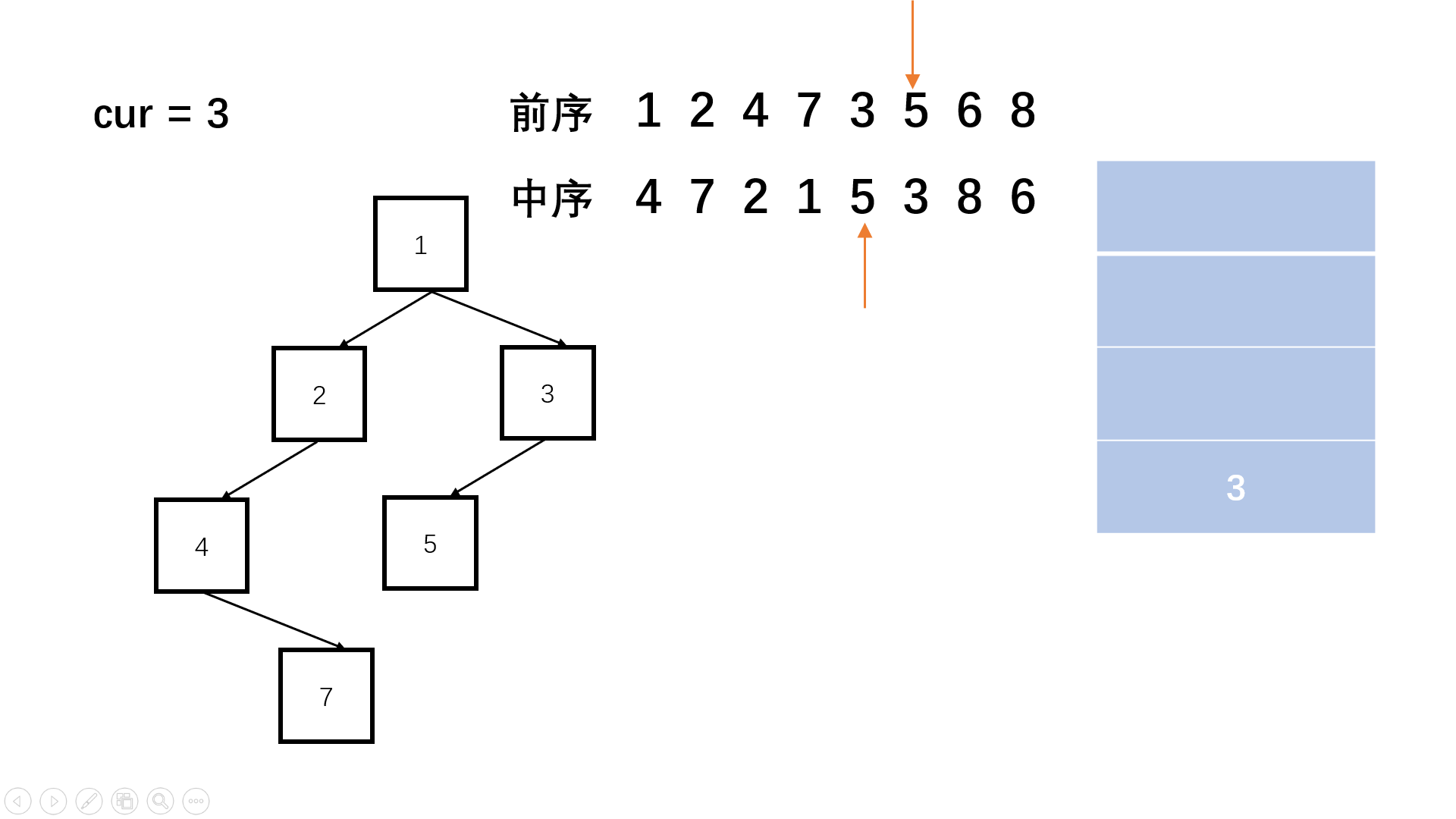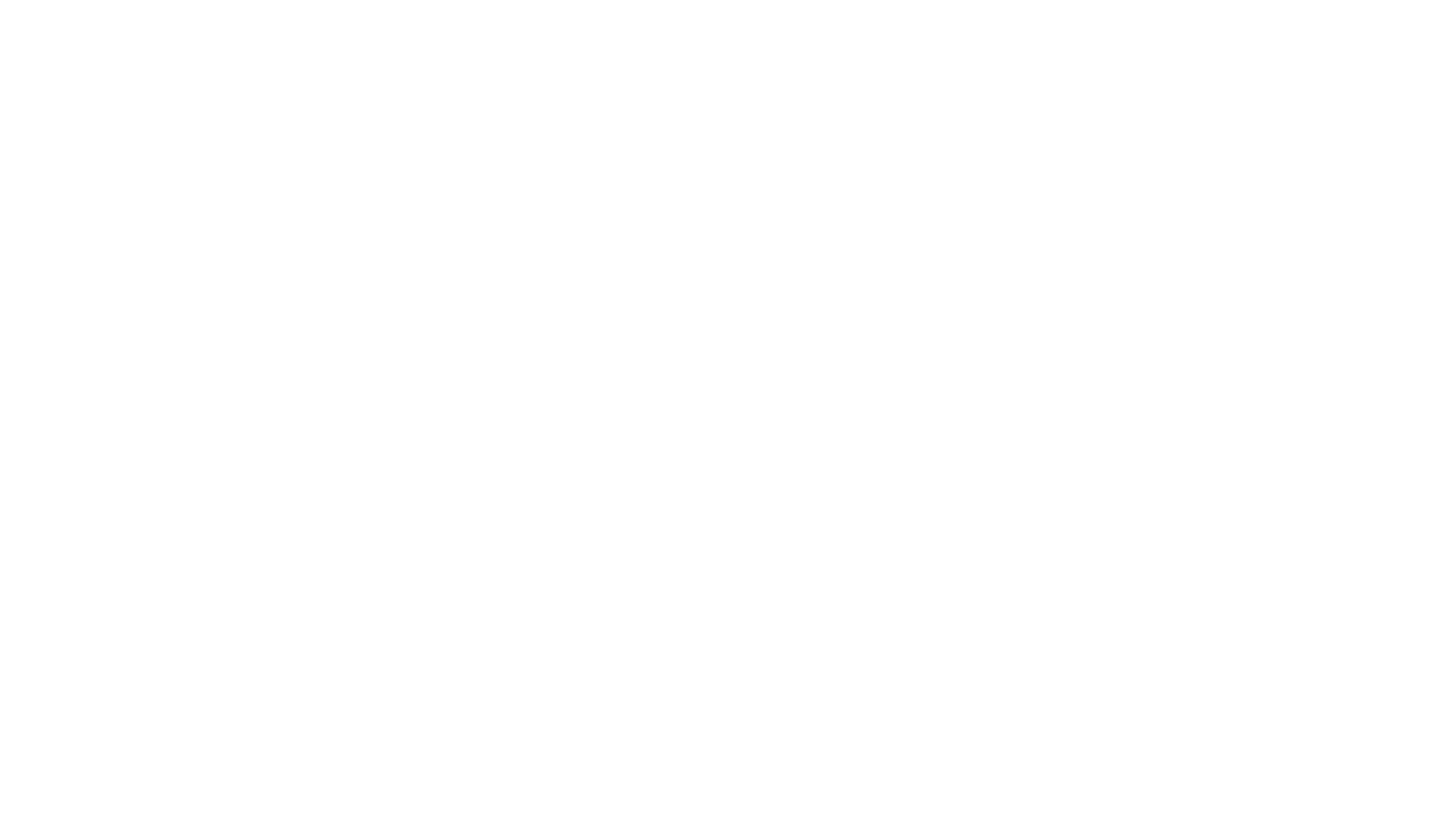
step 1：首先前序遍历第一个数字依然是根节点，并建立栈辅助遍历。
step 2：然后我们就开始判断，在前序遍历中相邻的两个数字必定是只有两种情况：要么前序后一个是前一个的左节点；要么前序后一个是前一个的右节点或者其祖先的右节点。
step 3：我们可以同时顺序遍历pre和vin两个序列，判断是否是左节点，如果是左节点则不断向左深入，用栈记录祖先，如果不是需要弹出栈回到相应的祖先，然后进入右子树，整个过程类似非递归前序遍历。

class Solution:
    def reConstructBinaryTree(self , pre: List[int], vin: List[int]) -> TreeNode:
        n = len(pre)
        m = len(vin)
        if n == 0 or m == 0:
            return None
        s = []
        root = TreeNode(pre[0])
        cur = root
        j = 0
        for i in range(1,n):
            # 后一个是前一个的左孩子
            if cur.val != vin[j]:
                cur.left = TreeNode(pre[i])
                s.append(cur)
                cur = cur.left
            # 后一个是前一个的右孩子，或者祖先的右孩子
            else:
                # 找到合适的cur，然后确定他的右孩子
                j = j + 1
                # 弹出到符合的祖先
                while s and s[-1].val == vin[j]:
                    cur = s.pop()
                    j = j + 1
                # 给cur添加右节点
                cur.right = TreeNode(pre[i])
                cur = cur.right
        return root

时间复杂度：O(n)，其中 n 为数组长度，即二叉树的节点数，遍历一次数组，弹出栈的循环最多进行n次。
空间复杂度：O(n)，栈空间最大深度为 n，重建的二叉树空间属于必要空间，不属于辅助空间。

41.输出二叉树的右视图

• 小试牛刀

41.1 递归建树+DFS

首先建树方面，前序遍历是根左右的顺序，中序遍历是左根右的顺序，因为节点值互不相同，我们可以根据在前序遍历中找到根节点（每个子树部分第一个就是），再在中序遍历中找到对应的值，从其左右分割开，左边就是该树的左子树，右边就是该树的右子树，于是将问题划分为了子问题。

而打印右视图即找到二叉树每层最右边的节点元素，我们可以采取dfs（深度优先搜索）遍历树，根据记录的深度找到最右值。

step 1：首先检查两个遍历序列的大小，若是为0，则空树不用打印。
step 2：建树函数根据上述说，每次利用前序遍历第一个元素就是根节点，在中序遍历中找到它将二叉树划分为左右子树，利用l1 r1 l2 r2分别记录子树部分在数组中分别对应的下标，并将子树的数组部分送入函数进行递归。
step 3：dfs打印右视图时，使用哈希表存储每个深度对应的最右边节点，初始化两个栈辅助遍历，第一个栈记录dfs时的节点，第二个栈记录遍历到的深度，根节点先入栈。
step 4：对于每个访问的节点，每次左子节点先进栈，右子节点再进栈，这样访问完一层后，因为栈的先进后出原理，每次都是右边被优先访问，因此我们在哈希表该层没有元素时，添加第一个该层遇到的元素就是最右边的节点。
step 5：使用一个变量逐层维护深度最大值，最后遍历每个深度，从哈希表中读出每个深度的最右边节点加入数组中。

from collections import defaultdict

class Solution:
    # 通过前序和中序，构建二叉树
    def buildTree(self, xianxu: List[int], l1: int, r1 :int, zhongxu: List[int], l2: int, r2:int):
        if l1 > r1 or l2 > r2:
            return None
        # 构建节点
        root = TreeNode(xianxu[l1])
        # 用来保存根节点在中序遍历列表的下标
        rootIndex = 0
        # 寻找根节点
        for i in range(l2, r2+1):
            if zhongxu[i] == xianxu[l1]:
                rootIndex = i
                break
        # 左子树的大小
        leftsize = rootIndex - l2
        # 右子树的大小
        rightsize = r2 - rootIndex
        # 递归构建左子树和右子树，注意边界值
        root.left = self.buildTree(xianxu, l1+1, l1+leftsize, zhongxu, l2, l2+leftsize-1)
        root.right = self.buildTree(xianxu, r1-rightsize+1, r1, zhongxu, rootIndex+1, r2)
        return root
    
    def rightSideView(self, root: TreeNode):
        # 哈希表用于存储每个深度对应的最右边的节点
        mp = defaultdict(int)
        # 记录最大深度
        max_depth = -1
        # 维护深度访问节点、维护dfs时的深度
        nodes, depths = [], []
        nodes.append(root)
        depths.append(0)
        # 因为栈是先进后出，所以右边的节点会被先处理
        # 所以哈希表中记录的一定是每一层的最右边的节点
        while nodes:
            node = nodes.pop()
            depth = depths.pop()
            if node:
                # 维护二叉树的最大深度
                max_depth = max([max_depth, depth])
                # 如果不存在对应深度的节点，才会插入
                if mp[depth] == 0:
                    mp[depth] = node.val
                nodes.append(node.left)
                nodes.append(node.right)
                depths.append(depth+1)
                depths.append(depth+1)
        res = []
        for i in range(max_depth+1):
            res.append(mp[i])
        return res
            
    def solve(self , xianxu: List[int], zhongxu: List[int]) -> List[int]:
        res = []
        # 空节点
        if len(xianxu) == 0:
            return res
        # 建立二叉树
        root = self.buildTree(xianxu, 0, len(xianxu)-1, zhongxu, 0, len(zhongxu)-1)
        # 找每一层最右边的节点
        return self.rightSideView(root)

时间复杂度：$O(n^2)$，建树部分递归为O(n)，中序遍历中寻找根节点最坏O(n)，dfs每个节点访问一遍O(n)，故为 $O(n^2)$。
空间复杂度：$O(n)$，递归栈、哈希表、栈的空间都为O(n)。

41.2 哈希表优化的递归建树+层次遍历

对于方法一中每次要寻找中序遍历中的根节点很浪费时间，我们可以利用一个哈希表直接将中序遍历的元素与前序遍历中的下标做一个映射，后续查找中序根节点便可以直接访问了。 同时除了深度优先搜索可以找最右节点，我们也可以利用层次遍历，借助队列，找到每一层的最右。值得注意的是：每进入一层，队列中的元素个数就是该层的节点数。 因为在上一层他们的父节点将它们加入队列中的，父节点访问完之后，刚好就是这一层的所有节点。

step 1：首先检查两个遍历序列的大小，若是为0，则空树不用打印。
step 2：遍历前序遍历序列，用哈希表将中序遍历中的数值与前序遍历的下标建立映射。
step 3：按照方法一递归划分子树，只是可以利用哈希表直接在中序遍历中定位根节点的位置。
step 4：建立队列辅助层次遍历，根节点先进队。
step 5：用一个size变量，每次进入一层的时候记录当前队列大小，等到size为0时，便到了最右边，记录下该节点元素。

from collections import defaultdict
import queue

class Solution:
    dic = defaultdict(int)
    # 通过前序和中序，构建二叉树
    def buildTree(self, xianxu: List[int], l1: int, r1 :int, zhongxu: List[int], l2: int, r2:int):
        if l1 > r1 or l2 > r2:
            return None
        root = TreeNode(xianxu[l1])
        # 用来保存根节点在中序遍历列表的下标
        rootIndex = self.dic[xianxu[l1]]
        # 左子树的大小
        leftsize = rootIndex - l2
        # 递归构建二叉树
        root.left = self.buildTree(xianxu, l1+1, l1+leftsize, zhongxu, l2, rootIndex-1)
        root.right = self.buildTree(xianxu, l1+leftsize+1, r1, zhongxu, rootIndex+1, r2)
        return root
    
    def rightSideView(self, root: TreeNode):
        res = []
        q = queue.Queue()
        q.put(root)
        while not q.empty():
            size = q.qsize()
            while size:
                size = size - 1
                temp = q.get()
                if temp.left:
                    q.put(temp.left)
                if temp.right:
                    q.put(temp.right)
                if size == 0:
                    res.append(temp.val)
        return res
            
    def solve(self , xianxu: List[int], zhongxu: List[int]) -> List[int]:
        res = []
        # 空节点
        if len(xianxu) == 0:
            return res
        for i in range(len(zhongxu)):
            self.dic[zhongxu[i]] = i
        # 建立二叉树
        root = self.buildTree(xianxu, 0, len(xianxu)-1, zhongxu, 0, len(zhongxu)-1)
        # 找每一层最右边的节点
        return self.rightSideView(root)

时间复杂度：O(n)，其中 n 为二叉树节点个数，每个节点访问一次，哈希表直接访问数组中的元素。
空间复杂度：O(n)，递归栈深度、哈希表、队列的空间都为O(n)。