Leetcode 动态规划(1)动态规划入门
1、斐波那契数(Leetcode.509)
方法一、暴力递归
class Solution {
public:
int fib(int n) {
if(n<=1){
return n;
}
return fib(n-1)+fib(n-2);
}
};方法二、动态规划
dp[i]含义:第i个斐波那契数的数值
递推公式:dp[i]=dp[i-1]+dp[i-2]
初始化:dp[0]=0,dp[1]=1
遍历顺序:从前向后依次遍历来完成填表
class Solution {
public:
int fib(int n) {
if(n<=1){
return n;
}
vectordp(n+1,0);
dp[1]=1;
for(int i=2;i<=n;i++){
dp[i]=dp[i-1]+dp[i-2];
}
return dp[n];
}
}; 优化:我们可以发现上述的过程中我们只用维护两个数值,即dp[i-1]和dp[i-2]
class Solution {
public:
int fib(int n) {
if(n<=1){
return n;
}
//用a表示i-2的值,b表示i-1的值,不断更新a和b
int a=0;
int b=1;
for(int i=2;i<=n;i++){
int c=a+b;
a=b;
b=c;
}
return b;
}
};2、爬楼梯(Leetcode.70)
解题思想:任一楼梯只能由该楼梯的前一个楼梯和前前一个楼梯到达,故到达该楼梯的方法数等于前两个楼梯的方法数总和
方法一、暴力递归
class Solution {
public:
int climbStairs(int n) {
if(n<=1){
return 1;
}
return climbStairs(n-1)+climbStairs(n-2);
}
};方法二、递归+记忆化搜索
class Solution {
public:
int process(int n,vector&res){
if(res[n]!=-1){
return res[n];
}
if(n<=1){
return 1;
}
res[n]=process(n-1,res)+process(n-2,res);
return res[n];
}
int climbStairs(int n) {
if(n<=1){
return 1;
}
vectorres(n+1,-1);
return process(n-1,res)+process(n-2,res);
}
}; 方法三、动态规划
dp[i]含义:爬第i个楼层的方法数
递推公式:dp[i]=dp[i-1]+dp[i-2]
初始化:dp[0]=1,dp[1]=1
遍历顺序:从前向后依次遍历来完成填表
class Solution {
public:
int climbStairs(int n) {
if(n<=1){
return 1;
}
vectordp(n+1,1);
for(int i=2;i<=n;i++){
dp[i]=dp[i-1]+dp[i-2];
}
return dp[n];
}
}; 优化:维护两个数值即可
class Solution {
public:
int climbStairs(int n) {
if(n<=1){
return 1;
}
int a=1;int b=1;
for(int i=2;i<=n;i++){
int c=a+b;
a=b;
b=c;
}
return b;
}
};3、使用最小花费爬楼梯(Leetcode.746)
解题思想:任一楼梯只能由该楼梯的前一个楼梯和前前一个楼梯到达,故到达该楼梯的最小花费数等于到达前两个楼梯的最小花费数再加上从前两个楼梯向上爬的费用的最小值
方法一、暴力递归
class Solution {
public:
//暴力递归的过程
int process(vector&cost,int index){
if(index==0||index==1){
return 0;
}
//该楼梯的最小费用
return min(process(cost,index-1)+cost[index-1],process(cost,index-2)+cost[index-2]);
}
int minCostClimbingStairs(vector& cost) {
if(cost.size()<=1){
return 1;
}
return process(cost,cost.size());
}
}; 方法二、动态规划
dp[i]含义:爬第i个楼层的最小费用
递推公式:dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])
初始化:dp[0]=0,dp[1]=0
遍历顺序:从前向后依次遍历来完成填表
class Solution {
public:
int minCostClimbingStairs(vector& cost) {
vectordp(cost.size()+1,0);
for(int i=2;i<=cost.size();i++){
dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
}
return dp[cost.size()];
}
}; 优化:
class Solution {
public:
int minCostClimbingStairs(vector& cost) {
int a=0;int b=0;
for(int i=2;i<=cost.size();i++){
int c=min(a+cost[i-1],b+cost[i-2]);
b=a;
a=c;
}
return a;
}
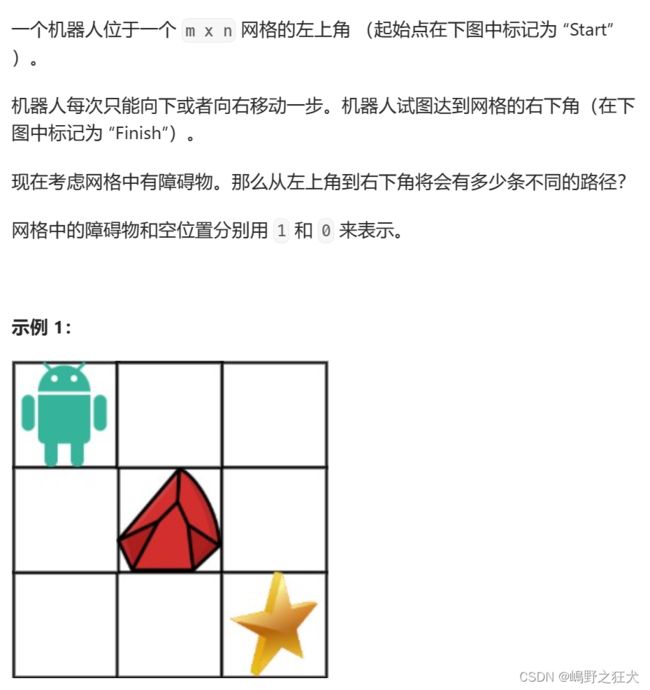
}; 4、不同路径(Leetcode.62)
解题思想:某位置只能从该位置的上方和该位置的左方出发得到,故到达某位置的方法数由两种位置的方法数相加得到,值得注意的是,最上方的一行位置只能由起始点往右到达,最左方的一列位置只能由起始点向下到达,到达这些位置的方法数为一
方法一、暴力递归
class Solution {
public:
int process(int row,int col){
//当到达最上方和最左方时只有一种方法,此时返回
if(row==1){
return 1;
}
if(col==1){
return 1;
}
//当前位置可由该位置的上方和该位置的左方到达
return process(row-1,col)+process(row,col-1);
}
int uniquePaths(int m, int n) {
return process(m,n);
}
};方法二、动态规划
dp[i][j]含义:到达i行j列位置的方法数
递推公式:dp[i][j]=dp[i-1][j]+dp[i][j-1]
初始化:dp[i][0]=1,dp[0][j]=1(第一行位置全为1,第一列位置全为1)
遍历顺序:从前向后依次遍历来完成填表
class Solution {
public:
int uniquePaths(int m, int n) {
vector>dp(m,vector(n,0));
for(int i=0;i 优化:滚动数组的优化方式,节省内存空间
class Solution {
public:
int uniquePaths(int m, int n) {
vectordp(n,1);
for(int i=1;i 5、不同路径II(Leetcode.63)
解题思想:与上一题大致相同,值得注意的是,当我们所求的位置的前一个位置有障碍时,则不能累加有障碍位置的方法数,如果所求位置就有障碍的话,直接跳过即可,而在初始化时,如果最上方位置有障碍物,则在障碍物右边的位置都无法到达,记为0,同理如果最左方位置有障碍物,则在障碍物下边的位置都无法到达
方法一、暴力递归
class Solution {
public:
int process(vector>& obstacleGrid,vector>&start,int row,int col){
if(obstacleGrid[row-1][col-1]){
return 0;
}
if(row==1){
return start[0][col-1];
}
if(col==1){
return start[1][row-1];
}
return process(obstacleGrid,start,row-1,col)+process(obstacleGrid,start,row,col-1);
}
int uniquePathsWithObstacles(vector>& obstacleGrid) {
//打一张表来记录我们后续递归到哪些位置返回1,哪些位置返回0
//我们只需要记录最左边和最上边的位置,如果用m*n二维数组的话浪费空间
//折叠一下表,用一张2*max(m,n)的表来代替即可
int m=obstacleGrid.size();
int n=obstacleGrid[0].size();
vector>start(2,vector(max(m,n),0));
for(int i=0;i 方法二、递归+记忆化搜索
class Solution {
public:
int process(vector>& obstacleGrid,vector>&start,
vector>&res,int row,int col){
if(obstacleGrid[row-1][col-1]){
return 0;
}
if(res[row-1][col-1]!=-1){
return res[row-1][col-1];
}
if(row==1){
return start[0][col-1];
}
if(col==1){
return start[1][row-1];
}
res[row-1][col-1]=process(obstacleGrid,start,res,row-1,col)+process(obstacleGrid, start,res,row, col-1);
return res[row-1][col-1];
}
int uniquePathsWithObstacles(vector>& obstacleGrid) {
//打一张表start来记录我们后续递归到哪些位置返回1,哪些位置返回0
//我们只需要记录最左边和最上边的位置,如果用m*n二维数组的话浪费空间
//折叠一下表,用一张2*max(m,n)的表来代替即可
//暴力递归超时,学会记忆化搜索,再打一张表memory来记录一下已知的结果
vector>memory(obstacleGrid.size(),vector(obstacleGrid[0].size(),-1));
int m=obstacleGrid.size();
int n=obstacleGrid[0].size();
vector>start(2,vector(max(m,n),0));
for(int i=0;i 方法三、动态规划
lass Solution {
public:
int uniquePathsWithObstacles(vector>& obstacleGrid) {
vector>dp(obstacleGrid.size(),vector(obstacleGrid[0].size(),0));
for(int i=0;i 优化:依然是进行空间上的优化
class Solution {
public:
int uniquePathsWithObstacles(vector>& obstacleGrid) {
vectordp(obstacleGrid[0].size(),0);
for(int i=0;i=1&&!obstacleGrid[i][j-1]){
dp[j]+=dp[j-1];
}
}
}
return dp[obstacleGrid[0].size()-1];
}
}; 6、整数拆分(Leetcode.343)
解题思想:对于任一整数,我们可以选择拆成两个或者多个整数,如给定数n,我们可以将其拆成i和n-i两个整数,也可以将其拆成i和一个还可以继续拆的(n-i),分别比较并记录该整数拆成不同数的乘积最大值,并返回结果
方法一、递归加记忆化搜索
后续我将不再提供暴力递归的方法,其时间复杂度过高,不如打一张表记录相同子问题的结果
class Solution {
public:
int process(int n,vector&res){
if(res[n]){
return res[n];
}
for(int i=1;i<=n/2;i++){
res[n]=max(res[n],max(process(n-i,res)*i,(n-i)*i));
}
return res[n];
}
int integerBreak(int n) {
vectorres(n+1,0);
return process(n,res);
}
}; 方法二、动态规划
这里有人将其理解为背包问题,即选择数装满一个容量为n的背包,这些数的最大乘积是多少,当然这里的数可以重复选取,所以是完全背包问题,我个人认为这题理解成背包反而增加了难度
class Solution {
public:
int integerBreak(int n) {
//dp[i]:将i拆分成k个正整数的最大乘积
vectordp(n+1,0);
dp[1]=0;dp[2]=1;
for(int i=3;i<=n;i++){
for(int j=1;j 7、不同的二叉搜索树(Leetcode.96)
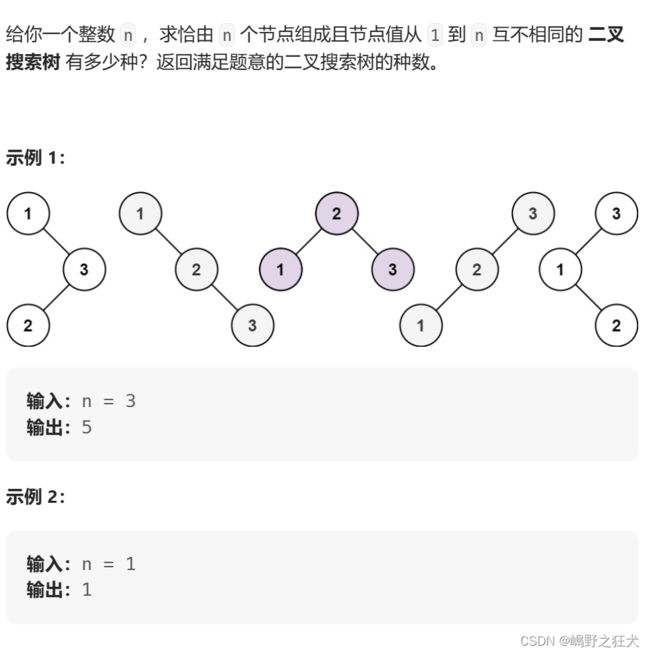
解题思想:在求n个节点所组成的二叉搜索树的总数时,不妨将节点1到节点n依次作为根节点,那么在选取节点i作为根节点时,左子树的节点数为i-1,右子树的节点数为n-i,按照这样的思想,我们持续划分,直到某一节点的左右子树节点数为0或1为止
方法一、递归加记忆化搜索
将每个节点作为根节点递归并打一张表来记录一下结果
class Solution {
public:
int process(int n,vector&res){
if(res[n]){
return res[n];
}
for(int i=1;i<=n;i++){
res[n]+=process(i-1,res)*process(n-i,res);
}
return res[n];
}
int numTrees(int n) {
vectorres(n+1,0);
res[0]=1;
res[1]=1;
return process(n,res);
}
}; 方法二、动态规划
dp[i]:从1到i这些节点所组成二叉搜索树的种数
class Solution {
public:
int numTrees(int n) {
vectordp(n+1,0);
dp[0]=1;
dp[1]=1;
for(int i=2;i<=n;i++){
for(int j=1;j<=i;j++){
dp[i]+=dp[j-1]*dp[i-j];
}
}
return dp[n];
}
}; 总结:
这些题目作为想要尝试动态规划的新手来说是非常适合的,不涉及一些比较难的动态规划问题,按照顺序理解并掌握这些动态规划的问题,就可以算是动态规划入门了