数据并行(DP)、张量模型并行(TP)、流水线并行(PP)

数据并行

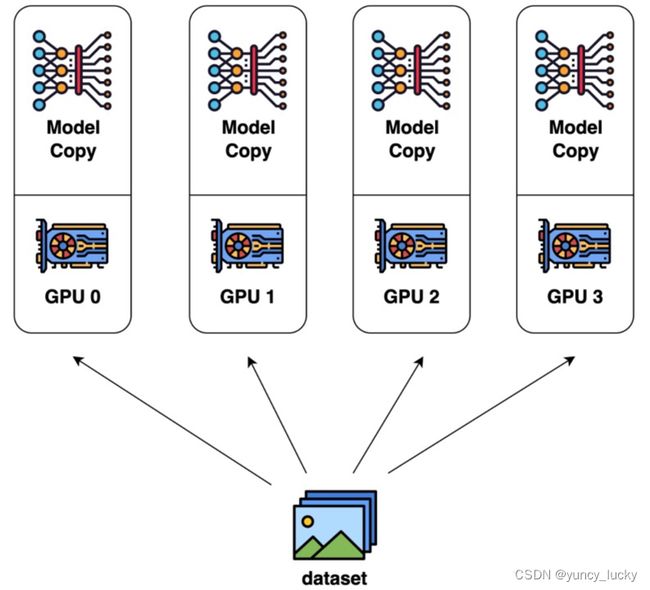
数据集分为n块，每块随机分配到m个设备(worker)中，相当于m个batch并行训练n/m轮，模型也被复制为n块，每块模型均在每块数据上进行训练，各自完成前向和后向的计算得到梯度，对梯度进行更新，更新后，再传回各个worker。以确保每个worker具有相同的模型参数。

三种主流数据并行的实现方式，详见：图解大模型训练之：数据并行上篇(DP, DDP与ZeRO) - 知乎

图解大模型训练之：数据并行下篇( DeepSpeed ZeRO，零冗余优化) - 知乎

下图1：每个设备分1份数据

 下图2：每个设备分4份数据

数据不切分的话，就是总共N-1次传输中每次传输数据大小为O（O是模型参数量），数据流转完整一圈仍然需要(N-1)*O的时间，传统参数服务器的总时间没区别了。如果每个GPU只和其相邻的两块GPU通讯，形成一个环，则单卡通讯量近似2*O，全卡近似为2*N*O。

数据并行中，每个GPU上都复制了一份完整模型，当模型变大时，很容易打爆GPU的显存，那要怎么办呢

模型并行

参考：

论文：https://arxiv.org/abs/1909.08053

[细读经典]Megatron论文和代码详细分析(1) - 知乎

图解大模型训练之：张量模型并行(TP)，Megatron-LM - 知乎

由于模型巨大，无法装入单个GPU，此时需要模型并行。

模型并行是包含范围很广的一类技术。它会在多个 worker 之间划分模型的各个层。就其本质而言，模型并行性的计算和通信因模型结构而异，因此在实现上有很大的工作量。DeepSpeed 借用了英伟达的 Megatron-LM 来为基于 Transformer 的语言模型提供大规模模型并行功能。模型并行会根据 worker 数量成比例地减少显存使用量，也是这三种并行度中显存效率最高的。但是其代价是计算效率最低。

• 显存效率：模型并行会根据 worker 数量成比例地减少显存使用量。至关重要的是，这是减少单个网络层的激活显存的唯一方法。DeepSpeed 通过在模型并行 worker 之间划分激活显存来进一步提高显存效率。
• 计算效率：由于每次前向和反向传播中都需要额外通信激活值，模型并行的计算效率很低。模型并行需要高通信带宽，并且不能很好地扩展到通信带宽受限的节点。此外，每个模型并行worker 都会减少每个通信阶段之间执行的计算量，从而影响计算效率。模型并行性通常与数据并行性结合使用，以在内存和计算效率之间进行权衡。

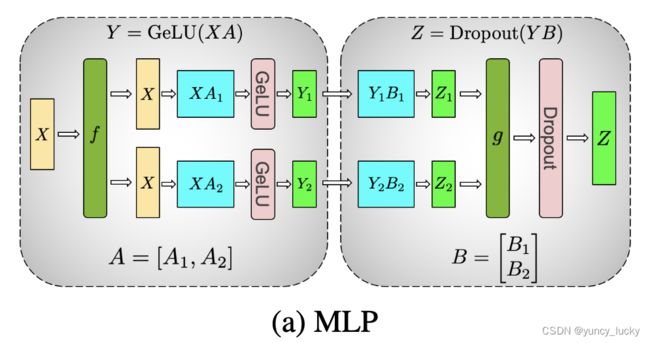
在模型并行中，每个 GPU 仅处理张量的一部分，并且仅当某些算子需要完整的张量时才触发聚合操作。我们可以将其点积部分写为 Y=GeLU(XA) ，其中 X 和 Y 是输入和输出向量， A 是权重矩阵。

如果以矩阵形式表示的话，很容易看出矩阵乘法可以如何在多个 GPU 之间拆分:

图a，对A采用列切割，对B采用行切割，这样设计的原因是，尽量保证各GPU上的计算相互独立，减少通讯量。对A来说，需要做一次GELU的计算，而GELU函数是非线形的，它的性质如下：

也就意味着，如果对A采用行切割，我们必须在做GELU前，做一次AllReduce，这样就会产生额外通讯量。但是如果对A采用列切割，那每块GPU就可以继续独立计算了。一旦确认好A做列切割，那么也就相应定好B需要做行切割了。

图b，左侧方框中的2个dropout，在初始化时需要用不同的随机种子。因为这样才等价于对完整的dropout做初始化，然后再切割。右侧方框中的dropout，需要用相同的随机种子（虽然右边只画了1个dropout，但其实是2个dropout，每块GPU上各一个，因为此时两块GPU上的输出已经AllReduce，是完全一致的。做完AllReduce后，两块GPU继续独立计算，因此实际上有两个dropout）。

可以发现，attention的多头计算简直是为张量模型并行量身定做的，因为每个头上都可以独立计算，最后再将结果concat起来。也就是说，可以把每个头的参数放到一块GPU上。

对三个参数矩阵Q，K，V，按照“列切割”，每个头放到一块GPU上，做并行计算。对线性层B，按照“行切割”。切割的方式和MLP层基本一致，其forward与backward原理也一致，这里不再赘述。
最后，在实际应用中，并不一定按照一个head占用一块GPU来切割权重，我们也可以一个多个head占用一块GPU，这依然不会改变单块GPU上独立计算的目的。所以实际设计时，我们尽量保证head总数能被GPU个数整除。

流水线并行(Pipeline Parallelism)

参考：

图解大模型训练之：流水线并行（Pipeline Parallelism），以Gpipe为例 - 知乎

【深度学习】【分布式训练】一文捋顺千亿模型训练技术：流水线并行、张量并行和3D并行 - 知乎

朴素的模型并行存在GPU利用度不足，中间结果消耗内存大的问题。而Gpipe提出的流水线并行，就是用来解决这两个主要问题的。

流水线并行的核心思想是：在模型并行的基础上，进一步引入数据并行的办法，即把原先的数据再划分成若干个batch，送入GPU进行训练。未划分前的数据，叫mini-batch。在mini-batch上再划分的数据，叫micro-batch。

终：

假设我们有2台机器（node0和node1），每台机器上有8块GPU，GPU的编号为0~15。
我们使用这16块GPU，做DP/TP/PP混合并行，如下图：

• MP：模型并行组（Model Parallism）。假设一个完整的模型需要布在8块GPU上，则如图所示，我们共布了2个model replica（2个MP）。MP组为：[[g0, g1, g4, g5, g8, g9, g12, g13], [g2, g3, g6, g7, g10, g11, g14, g15]]
• TP：张量并行组（Tensor Parallism）。对于一个模型的每一层，我们将其参数纵向切开，分别置于不同的GPU上，则图中一共有8个TP组。TP组为：[[g0, g1], [g4, g5],[g8, g9], [g12, g13], [g2, g3], [g6, g7], [g10, g11], [g14, g15]]
• PP：流水线并行组（Pipeline Parallism）。对于一个模型，我们将其每一层都放置于不同的GPU上，则图中一共有4个PP组。PP组为：[[g0, g4, g8, g12], [g1, g5, g9, g13], [g2, g6, g10, g14], [g3, g7, g11, g15]]
• DP：数据并行组（Data Parallism）。经过上述切割，对维护有相同模型部分的GPU，我们就可以做数据并行，则图中共有8个DP组。DP组为[[g0, g2], [g1, g3], [g4, g6], [g5, g7], [g8, g10], [g9, g11], [g12, g14], [g13, g15]]