存储管理页面置换算法模拟实现及比较
存储管理页面置换算法模拟实现及比较
1、目的
存储管理的主要功能之一是合理地分配空间。请求页式管理是一种常用的虚拟存储管理技术。页式管理中页面置换算法,了解虚拟存储技术的特点,掌握请求页式存储管理的页面置换算法。
2、学年设计内容
(1)通过随机数产生一个指令序列,共320条指令。
指令的地址按下述原则生成:
①一半的指令是顺序执行的;
②四分之一的指令是均匀分布在前地址部分;
③四分之一的指令是均匀分布在前地址部分。
具体的实施办法是:
① 在[0,319]之间选一起点m;
② 顺序执行一条指令,即m+1条;
③ 向前地址[0,m—1]中执行一条指令m’;
④ 顺序执行一条指令,即m’+1条;
⑤ 向后地址(m’+2,319]执行一条指令m’’
⑥ 重复上述步骤①-⑤,直到执行320次指令。
(2)将指令序列变换成为页地址流。
假设:① 页面大小为1KB;
② 用户实寸容量为4页到32页;
③ 用户虚存容量为32KB。用户虚存容量32KB,每1KB中放10条指令,共320条指令(0319)。其中09为0页,1019为1页…310319为31页。
(3)使用不同的页面调度算法处理缺页中断,并计算不同实存容量下(4~32KB)的命中率。
① 先进先出算法(FIFO);
② 最近最少使用算法(LRU);
③ 最佳淘汰算法(OPT);先淘汰最不常用的页地址;
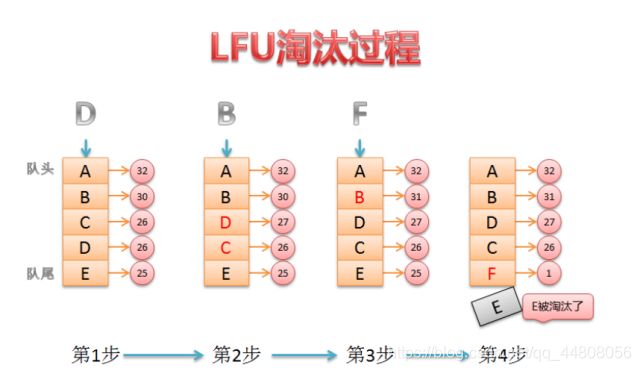
④ 最少访问页面算法(LFU)。
命中率的算法为: 命中率=1-缺页中断次数/页地址流长度
3、问题分析
(1)通过随机数产生一个指令序列,共320条指令
(2) 将指令序列变换成为页地址流
(3) 命中率=1-页面失效次数/页地址流长度;
(4) 理解各个页面调度算法
4、设计思路
根据对实验内容的理解,做一个整体框图,然后在一步一步地实现每个功能
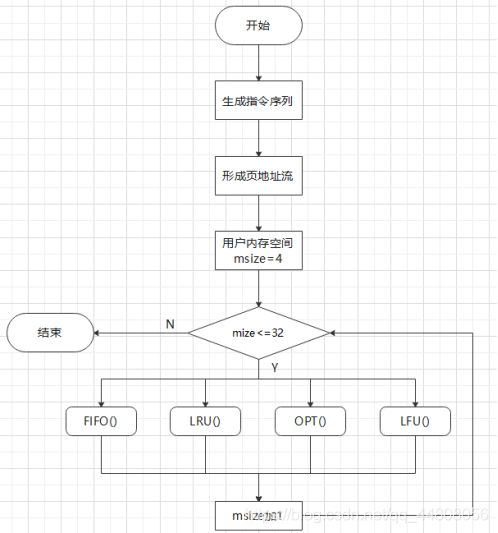
由框图可知,主要实现4个算法,首先理解一下每个算法:
(1) FIFO页面置换算法(先进先出算法):这个算法的基本思想是:总是先淘汰一些驻留在内存时间最长的页面,即先进入内存的页面先被置换掉。作业只要把进入内存的各个页面按进入的时间次序用链表链接起来,设定一个链表首指针指向进入内存最早的一个页面,新进入的页面放在链表的尾部,需要淘汰某一个页面时,总是淘汰替换指针所指向的页面即可。先进先出算法在程序按线性顺序访问逻辑地址空间时比较理想,否则效率不高。特别是在遇到循环执行的程序段时,往往会把频繁访问的页面,因其在内存驻留时间过长,而周期性地淘汰掉。

FIFO算法实现的逻辑框图:
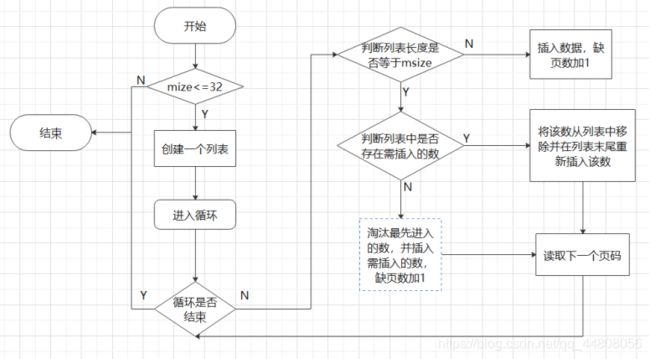
(2) LRU算法(最近最久未使用算法):本算法的基本思想是:如果某一页被访问了,那么它很可能马上又被访问;反之,如果某一页很长时间没有被访问,那么最近也不太可能会被访问。这种算法考虑了程序设计的局部性原理。其实质是:当需要置换一页时,选择最近一段时间内最久未使用的页面予以淘汰。以一个例子来解说,比较好好理解:假定系统为某进程分配了3个物理块,进程运行时的页面走向为 7 0 1 2 0 3 0 4,开始时3个物理块均为空,那么LRU算法是如下工作的:

LRU算法实现的逻辑框图:
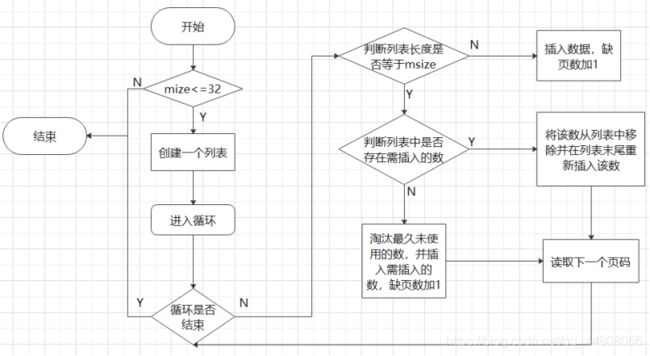
(3) OPT算法(最优算法):这是最理想的页面置换算法:从内存中移出以后不再使用的页面;如无这样的页面,则选择以后最长时间内不需要访问的页面。本算法因为页面访问的顺序是很难预知的,所以不是一种实际的方法。例如:假定系统为某进程分配了3个物理块,进程运行时的页面走向为 6,7,5,2,6,7,3,6,7,5,2,3,开始时3个物理块均为空,那么OPT算法是如下工作的:

(4) LFU算法(最少访问页面算法):本算法的原理是:要求在页面置换时置换引用计数最小的页面,因为经常使用的页应该有一个较大的引用次数。但是有些页在开始时使用次数很多,但以后就不再使用,这类页会长时间留在内存中,因此可以将引用计数寄存器定时右移一位,形成指数衰减的平均使用次数。此算法的特点是:因为在每一时间间隔内,只是用寄存器的一位来记录页的使用情况,因此,访问一次和访问10000次是等效的,次算法不能真正反映出页面的使用情况。
5、实现核心代码分析
(1)通过随机数产生一个指令序列,共320条指令。
在python中的random.randint(a,b)用于生成一个指定范围内的整数。其中参数a是下限,参数b是上限,生成的随机数n: a <= n <= b。根据实验内容来产生320个随机指令
① 在[0,319]之间选一起点m;
② 顺序执行一条指令,即m+1条;
③ 向前地址[0,m—1]中执行一条指令m’;
④ 顺序执行一条指令,即m’+1条;
⑤ 向后地址(m’+2,319]执行一条指令m’'⑥ 重复上述步骤①-⑤,直到执行320次指令。
def createRandomNum():
i = 0
while i < 320:
m = random.randint(0, 319) # 在[0,319]之间选一起点m;
num[i] = m + 1 # 顺序执行一条指令,即m+1条
m1 = random.randint(0, m-1)
i += 1
num[i] = m1 # 在[0,m-1]之间执行了一条指令
i += 1
num[i] = m1 + 1 # 顺序执行了一条指令
if m1 < 317:
m2 = random.randint(m1 + 2, 319)
i += 1
num[i] = m2 # 在[m1+2,319]之间执行了一条指令
print('**********生成320个随机数**********')
str = ''
for index, i in enumerate(num):
if index < 320:
str += '{}\t'.format(i)
if (index + 1) % 20 == 0:
str += '\n'
print(str)(2)将指令序列变换成为页地址流用户虚存容量32KB,每1KB中放10条指令,共320条指令(0~319)。
其中0到9为0页,10到19为1页…310~319为31页。这个地方开始理解有点错误,开始以为第0个指令到第9个指令算一页,但是这样导致之后页面调度算法太过于复杂难实现。所以再次理解题目的意思之后就由此将指令序列变换成为页地址流。
#将指令序列变换成为页地址流
def changeAsPage():
for index, i in enumerate(num):
if index < 320:
page[index] = int(i / 10)
print('**********转化为320个页码数**********')
str = ''
for index, i in enumerate(page):
str += '{}\t'.format(i)
if (index + 1) % 20 == 0:
str += '\n'
print(str)(3)不同的页面调度算法处理缺页中断
A. 先进先出算法(FIFO)
1.根据先进先出算法的理解,这种算法类似于队列,先进先出,像是在排队一样。所以根据这个特点,能够很快地想出如何实现。
2.接下来就考虑3种情况下,分别应该实施什么操作。
3.首先,当队列里的数小于msize(页帧)时,应该将数都加进队列中,此时缺页次数需加1,其次如果需加入的数在队列的存在时,只需移除它,并再将该数插入队列,来更新一下位置,此时是没有产生缺页的,最后就是队列的长度等于msize(页帧),并且插入的数不在队列中的时候,这时候就考虑淘汰最先进入队列的数,此时只需要使用列表的内置函数pop()就可以完成操作,然后插入即可,同时缺页数加1。
#先进先出算法(FIFO)
def FIFO(msize):
Q=[] #定义队列
diseffect=0 #缺页次数
for item in page:
if item in Q:
Q.remove(item)
Q.append(item)
elif len(Q)<msize:
Q.insert(0,item)
diseffect+=1
else:
Q.pop()
Q.insert(0,item)
diseffect += 1
return 1-diseffect/len(page)B. 最近最少使用算法(LRU)
1.根据最久未使用算法的理解,这种算法类似于堆栈,插入数据就往列表里加入,需淘汰时,淘汰列表里第一位数即可。
2.依旧考虑3种情况下,分别应该实施什么操作。
3.首先,当队列里的数小于msize(页帧)时,应该将数都加进队列中,此时缺页次数需加1,其次如果需加入的数在队列的存在时,只需移除它,并再将该数插入队列,来更新一下位置,此时是没有产生缺页的,最后就是队列的长度等于msize(页帧),并且插入的数不在队列中的时候,根据插入以及算法的特点,这时候只需要淘汰列表里的第一个数,使用列表的内置函数pop(0)就可以完成操作,然后插入即可,同时缺页数加1。
#最近最少使用算法(LRU)
def LRU(msize):
L=[] #堆栈
diseffect=0 #缺页次数
for item in page:
if item in L:
L.remove(item)
L.append(item)
elif len(L)<msize:
L.append(item)
diseffect+=1
else:
L.pop(0)
L.append(item)
diseffect += 1
return 1-diseffect/len(page)C. 最佳淘汰算法(OPT);
1.先淘汰最不常用的页地址;根据对最佳淘汰算法的理解,这种算法还是比较难实现的,我们需要找到插入数据之后最后出现的数并且存在列表当中的数,然后淘汰掉该数,并插入需要插入的数。
2.依旧考虑3种情况下,分别应该实施什么操作。
3.首先,当队列里的数小于msize(页帧)时,应该将数都加进队列中,此时缺页次数需加1,其次如果需加入的数在队列的存在时,只需移除它,并再将该数插入队列,来更新一下位置,此时是没有产生缺页的,最后就是队列的长度等于msize(页帧),并且插入的数不在队列中的时候,这时我们需要用列表s来记录插入数据之后的各个页码数的坐标,再考虑哪个页码最不常用,即比较哪个坐标最大,然后再到列表L中去除页码流最大坐标对应的数,然后插入即可,同时缺页数加1。
#最佳淘汰算法(OPT);先淘汰最不常用的页地址;
def OPT(msize):
L = []
diseffect = 0
for index, item in enumerate(page):
if item in L:
L.remove(item)
L.append(item)
elif len(L) < msize:
L.append(item)
diseffect += 1
else:
s=[] #用于存储列表L的数在页面流之后页码出现的坐标
page1 = page[index + 1:]
flag=False #用于做之后进入哪个条件的判断
for index,i in enumerate(L):
if i not in page1:
flag=True
break
else:
a = page1.index(i)
s.append(a)
if flag==True:
L.pop(index)
else:
maxindex = max(s)
index1 = L.index(page1[maxindex])
L.pop(index1)
L.append(item)
diseffect += 1
return 1 - diseffect / len(page)A.
D. 最少访问页面算法(LFU);
1.根据对最少访问算法的理解,开始理解有点误区,当时看到一个解释是在一段时间内淘汰被访问次数最少的页码,但是正确的理解应该是淘汰历史访问的的次数最少的页码。
2.依旧考虑3种情况下,分别应该实施什么操作。
3.首先,当队列里的数小于msize(页帧)时,应该将数都加进队列中,此时缺页次数需加1,其次如果需加入的数在队列的存在时,只需移除它,并再将该数插入队列,来更新一下位置,此时是没有产生缺页的,最后就是队列的长度等于msize(页帧),并且插入的数不在队列中的时候,这时我们需要用列表s记录历史访问的各个页码的次数,并用局部变量mincount记录每次最小访问的数,之后在列表中找出第一个与该数出现次数相同的数,淘汰掉该数,并插入需要插入的数,同时缺页数加1。
#最少访问页面算法(LFU),根据数据的历史访问频率来淘汰数据
def LFU(msize):
L = [] # 队列
diseffect = 0 # 缺页次数
for index,item in enumerate(page):
if item in L:
L.remove(item)
L.append(item)
elif len(L) < msize:
L.append(item)
diseffect += 1
else:
s=[] #用于存储历史访问的页码次数
page1=page[:index]
for i in page1:
s.append(page1.count(i))
mincount=min(s)
for item1 in page1:
if L.count(item1) == mincount:
L.remove(item1)
L.append(item)
break
diseffect += 1
return 1 - diseffect / len(page)4.
6、程序运行截图
产生的320个随机指令和其对应的页码数

各个算法在不同页帧下的命中率:
7、源代码
import random
num = [0 for i in range(0,325)] # 生成随机数会有溢出,所以数组长度设置大一点
page = [0 for i in range(0,320)]
def createRandomNum():
i = 0
while i < 320:
m = random.randint(0, 319) # 在[0,319]之间选一起点m;
num[i] = m + 1 # 顺序执行一条指令,即m+1条
m1 = random.randint(0, m-1)
i += 1
num[i] = m1 # 在[0,m-1]之间执行了一条指令
i += 1
num[i] = m1 + 1 # 顺序执行了一条指令
if m1 < 317:
m2 = random.randint(m1 + 2, 319)
i += 1
num[i] = m2 # 在[m1+2,319]之间执行了一条指令
print('**********生成320个随机指令**********')
str = ''
for index, i in enumerate(num):
if index < 320:
str += '{}\t'.format(i)
if (index + 1) % 20 == 0:
str += '\n'
print(str)
#将指令序列变换成为页地址流
def changeAsPage():
for index, i in enumerate(num):
if index < 320:
page[index] = int(i / 10)
print('**********转化为320个页码数**********')
str = ''
for index, i in enumerate(page):
str += '{}\t'.format(i)
if (index + 1) % 20 == 0:
str += '\n'
print(str)
#先进先出算法(FIFO)
def FIFO(msize):
Q=[] #定义队列
diseffect=0 #缺页次数
for item in page:
if item in Q:
Q.remove(item)
Q.append(item)
elif len(Q)<msize:
Q.insert(0,item)
diseffect+=1
else:
Q.pop()
Q.insert(0,item)
diseffect += 1
return 1-diseffect/len(page)
#最近最少使用算法(LRU)
def LRU(msize):
L=[] #堆栈
diseffect=0 #缺页次数
for item in page:
if item in L:
L.remove(item)
L.append(item)
elif len(L)<msize:
L.append(item)
diseffect+=1
else:
L.pop(0)
L.append(item)
diseffect += 1
return 1-diseffect/len(page)
#最佳淘汰算法(OPT);先淘汰最不常用的页地址;
def OPT(msize):
L = []
diseffect = 0
for index, item in enumerate(page):
if item in L:
L.remove(item)
L.append(item)
elif len(L) < msize:
L.append(item)
diseffect += 1
else:
s=[] #用于存储列表L的数在页面流之后页码出现的坐标
page1 = page[index + 1:]
flag=False #用于做之后进入哪个条件的判断
for index,i in enumerate(L):
if i not in page1:
flag=True
break
else:
a = page1.index(i)
s.append(a)
if flag==True:
L.pop(index)
else:
maxindex = max(s)
index1 = L.index(page1[maxindex])
L.pop(index1)
L.append(item)
diseffect += 1
return 1 - diseffect / len(page)
#最少访问页面算法(LFU),根据数据的历史访问频率来淘汰数据
def LFU(msize):
L = [] # 队列
diseffect = 0 # 缺页次数
for index,item in enumerate(page):
if item in L:
L.remove(item)
L.append(item)
elif len(L) < msize:
L.append(item)
diseffect += 1
else:
s=[] #用于存储历史访问的页码次数
page1=page[:index]
for i in page1:
s.append(page1.count(i))
mincount=min(s)
for item1 in page1:
if L.count(item1) == mincount:
L.remove(item1)
L.append(item)
break
diseffect += 1
return 1 - diseffect / len(page)
createRandomNum()
changeAsPage()
i=4
while i<33:
print("--- {} page frames---".format(i))
print("FIFO命中率为:{}".format(FIFO(i)))
print("LRU命中率为:{}".format(LRU(i)))
print("OPT命中率为:{}" .format(OPT(i)))
print("LFU命中率为:{}" .format(LFU(i)))
print()
i+=1
8、参考文献
[1] 几种缺页中断算法(FIFO,LRU与LFU)的实现过程:http://blog.chinaunix.net/uid-13246637-id-5185352.html
[2] FIFO、LRU、OPT页面调度算法及例子:https://blog.csdn.net/lingzhm/article/details/47417017?utm_medium=distribute.pc_relevant.none-task-blo g-BlogCommendFromMachineLearnPai2-1.nonecase&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase
[3] LRU算法原理解析 :https://www.cnblogs.com/linxiyue/p/10926944.html
[4] 图解缓存淘汰算法三之FIFO:https://www.cnblogs.com/geyifan/p/3830429.html
[5] Python列表(List):https://www.runoob.com/python/python-lists.html
[6] 操作系统存储管理实验课程设计报告:https://blog.csdn.net/zzh_569754126/article/details/51492348
[7] 操作系统 存储管理实验报告:https://blog.csdn.net/qq_43592352/article/details/106850352?utm_medium=distribute.pc_relevant.none-t ask-blog-baidujs-2