异常检测之PCA实战

目录

一、PCA原理

二、信用卡退款欺诈行为检测实战

1、数据介绍

 2、欺诈数据分析及特征衍生

3、特征分布分析及特征筛选

4、数据归一化处理

5、PCA模型构建及评估

划重点

---

        PCA是一个经典的线性降维算法，而降维算法可以先进行降维、再重构数据，那些难以重构的样本就是和整体分布差异较大的样本点，我们通过计算原始数据和重构数据的差异来识别出难以重构的样本，从而达到异常检测的目的。

一、PCA原理

        PCA（Principal Component Analysis，主成分分析）是一种常用的降维技术，用于从高维数据中提取最重要的特征，关键思想是通过找到能够最大程度保留原始数据方差的投影方向，将高维数据转换为低维空间。选择前 k 个主成分可以根据特征值的比例来确定，通常选择保留总方差的一定比例（例如，保留总方差的 95%）或者根据特定的业务需求来确定降维后的维度。 PCA 的计算过程如下：

        （1）数据标准化： 首先对原始数据进行标准化处理，使得每个特征具有零均值和单位方差。这是为了确保不同特征的尺度和方差差异不会对 PCA 的结果产生不良影响。

        （2）协方差矩阵计算： 计算标准化后数据的协方差矩阵。协方差矩阵描述了数据特征之间的线性相关性。对于一个 d 维数据集，协方差矩阵是一个 d×d 的对称矩阵，其中每个元素表示两个特征之间的协方差。

        （3）特征值分解： 对协方差矩阵进行特征值分解，得到特征值和对应的特征向量。特征向量表示了数据在新的坐标系下的主成分方向，而特征值则表示了数据在对应特征向量方向上的方差大小。

        （4）特征值排序： 将特征值按照从大到小的顺序进行排序，选择前 k 个最大的特征值及其对应的特征向量作为主成分。

        （5）投影转换： 将原始数据投影到选定的 k 个主成分上，得到降维后的数据集。投影转换涉及将每个数据样本乘以特征向量，从而在新的低维空间中表示原始数据。

二、信用卡退款欺诈行为检测实战

1、数据介绍

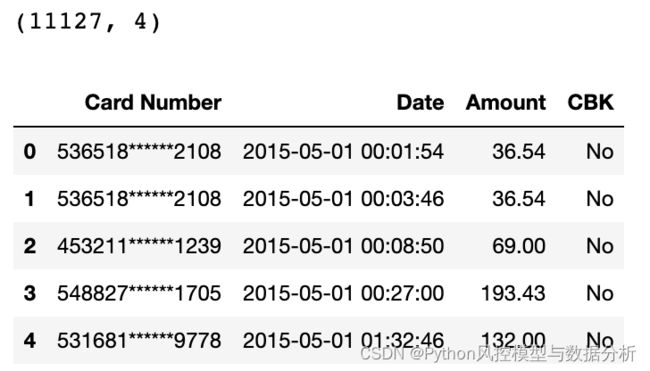
        使用信用卡退款欺诈行为检测数据，具体来源记不住了。样本量11127条，包括卡号、退款操作时间、金额、以及是否欺诈的标签CBK，这里我们还是通过无监督的方式来识别欺诈退款，然后用欺诈标签评估模型效果、并用于调整特征和模型。

 2、欺诈数据分析及特征衍生

（1）时间特征衍生

         数据结构比较简单，而整个数据的时间窗口都在2015-05一个月内，所以我们先从Date字段提取出周、日、时、分、秒等时间字段，考虑到周内、周末信用卡操作频次可能存在差异，所以也提取出weekday（周几）。另外CBK也映射为0-1值，便于后续处理。

（2）欺诈行为分析及分组特征衍生

        在很多场景里，聚集便意味着风险，这里我们也可以分组进行分析。数据集中提供了信用卡卡号，对于一个退款的欺诈用户而言，如果成功退款了一次，那么他一定会连续尝试、多次退款，所以可以查看一下是否存在短时间内频繁退款的情况。

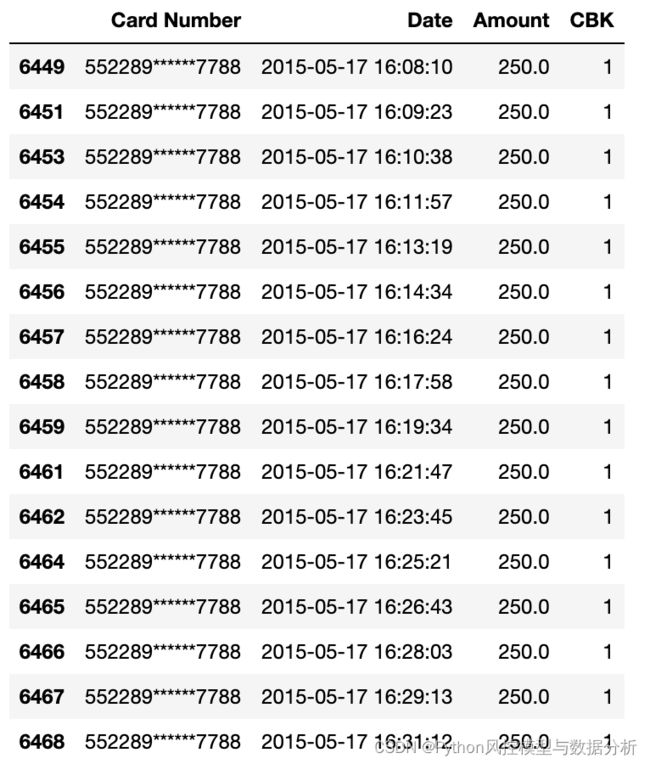
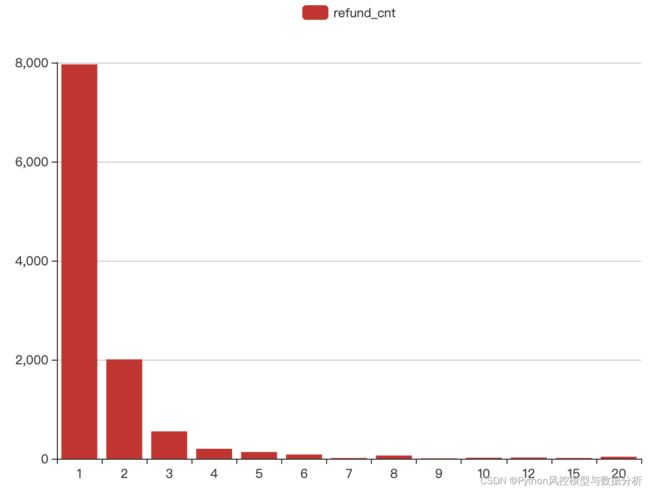
        如下图所示，存在部分信用卡在一个月内产生频繁退款的行为，结合欺诈标签进行分析，可以看到欺诈行为大多频繁退款的行为均存在异常。

         从微观角度来看，退款频数top1的信用卡在半小时内发起了20次退款，每隔1-2分钟发起一笔，且退款金额为固定值250，看起来很像是程序控制的随机时间间隔来发起退款行为。

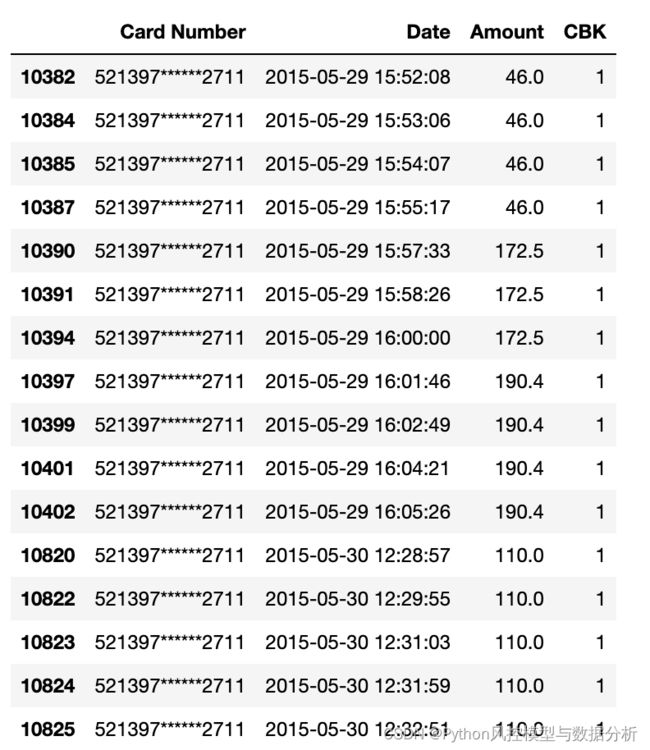
        再来看退款频次top2的信用卡，与上图情况相似，不同的是退款金额间隔几次会存在一定变化。

        另外，我们也可以发现部分高频退款行为的欺诈标签为0，与前面欺诈行为的区别在于退款金额不存在规律性。不过由于发生高频退款行为、而标签为未欺诈的数据较少（即从数据标签来看，高频退款的基本均为欺诈行为），这里为了方便不再额外去衍生高频退款行为下、金额规律性的特征，有兴趣的朋友可以尝试一下能否进一步提高识别欺诈的能力。

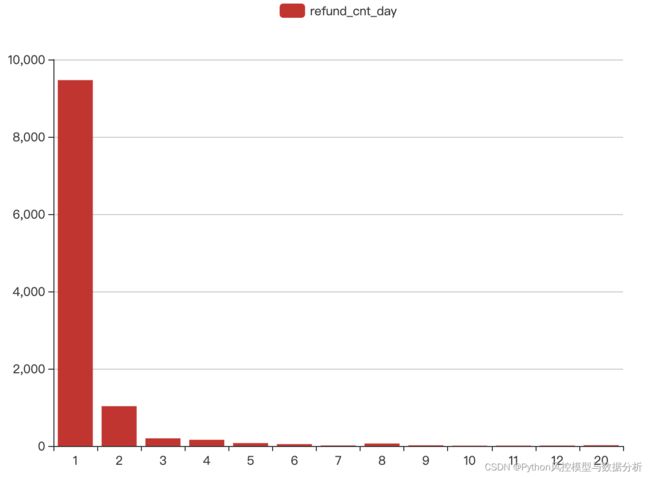
         根据上述欺诈行为分析，高频退款便可能存在着风险，这里简单衍生出按照信用卡分组的月度退款频数、天退款频数、hour退款频数等特征。

3、特征分布分析及特征筛选

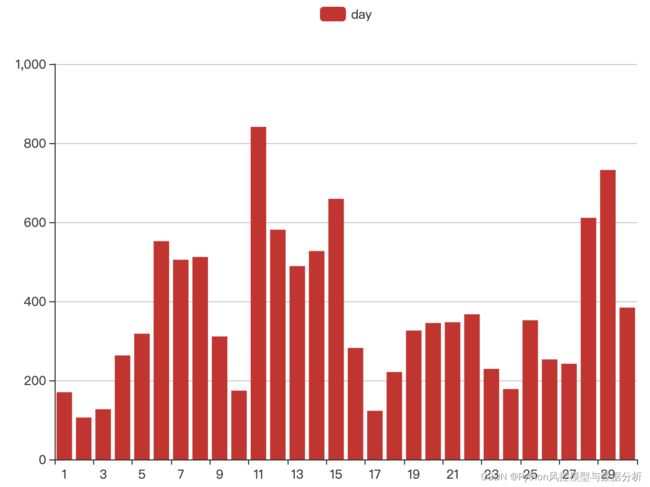
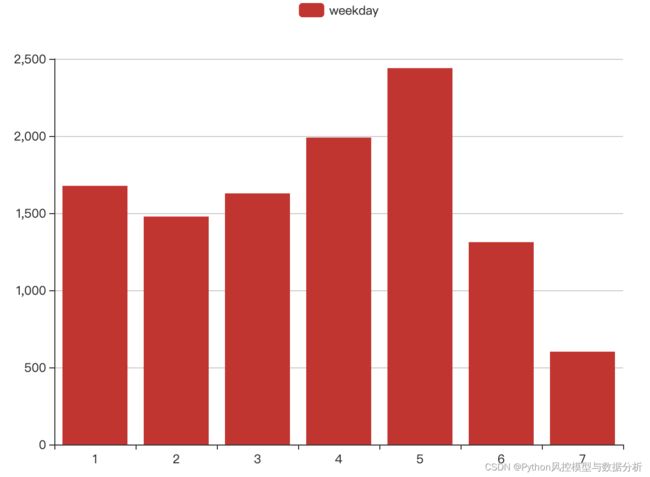
        首先，分别从天、周数、小时来进行特征分布分析。如下图所示，从1-30日内每隔几天就会有低频退款的day，即存在不规则的周期波动性，所以结合图二当天所在周几来看，周六日的退款频数明显低于周内，尤其是周末，而低频则意味着风险，所以day、weekday特征均保留。

        同理，hour特征分布来看，在凌晨1-7点的睡眠时间段之间交易频数偏低，且在这段时间发起退款行为难免让人疑惑，因此hour特征也保留入模。

        与上面不同，分钟数、秒数特征几乎没有什么规律可言，每分钟的退款频次几乎相近，对于欺诈识别没有什么贡献，因此剔除分钟数、秒数特征。

        最后再来看信用卡对应的退款频数特征，基本符合长尾分布，月度退款次数达多集中在2次以内、高频退款行为还是比较少的，根据其分布结合前文的欺诈分析，这部分特征可以极大地增强模型的欺诈异常识别能力

4、数据归一化处理

        在使用PCA降维、重构之前先将数据进行归一化，避免因为量纲、数据量级的不统一

df2_copy2=df2_copy.copy()
scaler = MinMaxScaler()

fea_list=['Amount', 'day','hour', 'weekday','refund_cnt','refund_cnt_day','refund_cnt_day_hour']
df2_copy2[fea_list]=scaler.fit_transform(df2_copy[fea_list])

5、PCA模型构建及评估

        最终入模变量保留 Amount，day，hour，weekday，refund_cnt，refund_cnt_day，refund_cnt_day_hour 共7个。在建模前我们先把数据集进行归一化来消除量纲差异、便于后续评估异常得分，然后按照8:2的比例随机划分出训练集、测试集，将训练集用于构建PCA，之后分别在训练集、测试集上进行数据重构，那些难以重构的样本就是和整体分布差异较大的样本点、因此使用样本的重构误差mae来作为异常得分，然后再使用ks、auc评估模型效果。

        可以看到在保留2个主成分的情况下，PCA在测试集上识别欺诈的auc达到了0.83

import numpy as np
from sklearn.decomposition import PCA
from scipy.stats import chi2

fea_list=['Amount', 'day','hour', 'weekday','refund_cnt','refund_cnt_day','refund_cnt_day_hour']

pca = PCA(n_components=2,whiten=False,random_state=1)
pca.fit(df2_copy2[df2_copy2['sample']=='train'][fea_list])
X_pca = pca.transform(df2_copy2[fea_list])

X_reconstructed = pca.inverse_transform(X_pca) # 数据重构
df2_copy2['mae_pca']= np.mean(np.abs(df2_copy2[fea_list] - X_reconstructed), axis=1) 
ks_auc_value(df2_copy2.CBK,df2_copy2.mae_pca)

'''
   output (0.6157866056255445, 0.8565583043200286)
'''

ks_auc_value(df2_copy2[df2_copy2['sample']=='train'].CBK,df2_copy2[df2_copy2['sample']=='train'].mae_pca)

'''
   output (0.6299455998590442, 0.8629379444545928)
'''
ks_auc_value(df2_copy2[df2_copy2['sample']=='test'].CBK,df2_copy2[df2_copy2['sample']=='test'].mae_pca)

'''
   output (0.5599423037296518, 0.8312342880692355)
'''

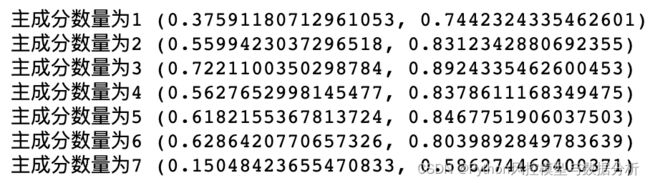
        因为数据集中包含欺诈标签，我们可以调整PCA保留的主成分数量来调整出一个精度更高的模型。特征数量为7，所以主成分数量分别从1-7进行训练评估，最终当主成分数量为3时，测试集的auc达到最大值0.89。

for n_components in range(1,8):
    pca = PCA(n_components=n_components,whiten=False,random_state=1)
    pca.fit(df2_copy2[df2_copy2['sample']=='train'][fea_list])
    X_pca = pca.transform(df2_copy2[fea_list])

    X_reconstructed = pca.inverse_transform(X_pca) 
    df2_copy2['mae_pca']= np.mean(np.abs(df2_copy2[fea_list] - X_reconstructed), axis=1) 
    print('主成分数量为{}'.format(n_components),ks_auc_value(df2_copy2[df2_copy2['sample']=='test'].CBK,df2_copy2[df2_copy2['sample']=='test'].mae_pca))
    
    

划重点

        关注威心公众号 Python风控模型与数据分析 ，回复 异常检测PCA实战 获取本文数据、完整代码！还可以获取更多理论知识与代码分享