机器学习 之 线性回归 平方损失函数 和 梯度下降算法 公式推导

1. 线性回归 Linear Regression

现在给出一个数据集$(a_1,b_1)(a_2,b_2)......(a_n,b_n)$，在这个线性回归模型中假设样本和噪声都服从高斯分布。问题需要根据给出的散点拟合一个最佳的 一次函数 即：
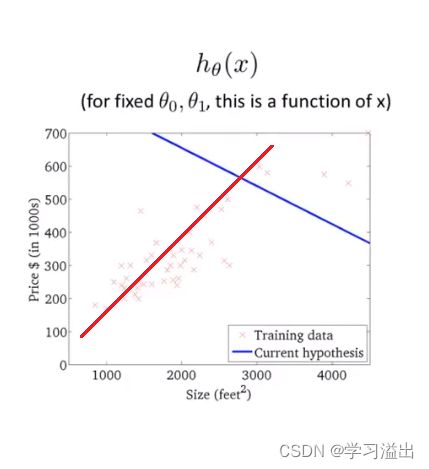
$$h={\theta }_{1}x+{\theta }_0$$如图，红色的叉为给出的数据集散点；蓝色的一次函数是我们需要进行拟合的直线；红色的一次函数则是这些散点真实的的拟合直线。（图片摘自吴恩达的网课）

2. 损失函数 Cost Function

现在我们的目标就是将拟合函数 $h={\theta }_{1}x+{\theta }_0$ 中的${\theta }_1$和${\theta }_0$不断逼近真实值。说白了，题目给出红色的叉，我们假设一条 一次函数 （蓝色） 直线，通过不断改变${\theta }_0,{\theta }_1$的值，将（蓝色）直线不断逼近真实的直线 （红色）。

那么问题来了，我怎么知道我现在拟合的一次函数是不是真实值 或者 和真实值差多少了呢？这里我们就需要一个评判标准，在机器学习里我们把它叫作 损失函数 或 代价函数。损失函数是用来估量模型的预测值h与真实值y的不一致程度。

2.1 平方损失函数 / 最小二乘法（Square Error Function / Ordinary Least Squares）

损失函数有很多种，其中平方损失函数(最小二乘法)适用于大多数的线性回归问题。而平方损失函数的基本原则是：
最优拟合直线应该是使各点到回归直线的距离和最小的直线，即平方和最小。
即损失函数的值越小，拟合的函数就越好。

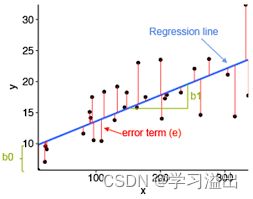
如图（随便在网上找的），平方损失函数即所有的红色的线的平方和。而将损失函数$J({\theta }_0,{\theta }_1)$写成数学公式即是：
$$J({\theta }_0,{\theta }_1)=\sum _{i=1}^m(h(x_i)-y_i{)}^2$$
其中$h(x)$是拟合的函数，$h(x_i)$为拟合函数上$x_i$对应的估计值，$y_i$为$x_i$对应的真实值。损失函数即是所有估计值减真实值的平方和。

在实际应用中，通常会用均方差（Mean Square Error）来作为损失函数，其中m为数据集的数量，即有m个散点 （有时会用2m），均方差公式为：
$$J({\theta }_0,{\theta }_1)=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x_i)-y_i{)}^2$$

此时，损失函数$J$对于单个变量${\theta }_0$或${\theta }_1$都为一个开口向上的二次函数（这里就不放图了）。
而损失函数$J({\theta }_0,{\theta }_1)$ 对于两个变量${\theta }_0,{\theta }_1$为一个碗状的函数。碗的最低点（损失函数的最小值），即是我们要寻找的最佳拟合时变量${\theta }_0,{\theta }_1$所对应的值。

3. 梯度下降 Gradient Descent

梯度下降算法是一个最优化算法，可以利用逼近法找到函数的局部极小值。现在我们有了损失函数，所要做的仅仅就是把损失函数降到最低，以找到最佳的拟合函数。梯度下降是一个不断迭代，直到收敛的算法（理想情况）。

对于一次函数，我们有两个变量需要利用梯度下降来逼近 — ${\theta }_0,{\theta }_1$。
对于任意一个变量${\theta }_j$，梯度下降的公式可表示为：
$${\theta }_j:={\theta }_j-\alpha \frac{d}{d_{\theta }{\theta }_j}J({\theta }_0,{\theta }_1)$$

其中：

1. := 为赋值符号。 a:=b 即将b的值赋给a
2. $\alpha$ 为学习率（learning rate）。如果学习率过小，梯度下降过程将很慢；如果学习率过大，梯度下降有可能不收敛，甚至发散。
3. $\frac{d}{d_{\theta }{\theta }_j}J({\theta }_0,{\theta }_1)$ 为收敛函数的导数，即收敛函数在该点处的切线斜率。因为上文提到过，收敛函数值越小，拟合的函数就越好。寻找收敛函数的极小值，即收敛函数的导数值越小，拟合的函数越好。$\frac{d}{d_{\theta }{\theta }_j}$是导数符号。
4. ${\theta }_0,{\theta }_1$ 是一对点，要同时更新。

那么如何在单个变量${\theta }_0,{\theta }_1$上逼近真实值呢？这时就需要分别对${\theta }_0,{\theta }_1$在损失函数公式中求偏导数。
这里用到复合函数求导和偏导数。
提示：
求导：$f(x)=x^2时f^{\prime }(x)=2x$
复合函数求导：$f[g(x){]}^{\prime }=f^{\prime }[g(x)]g^{\prime }(x)$

把损失函数带入梯度下降公式：
$${\theta }_j:={\theta }_j-\alpha \frac{d}{d_{\theta }{\theta }_j}\frac{1}{m}\sum _{i=1}^m(h(x_i)-y_i{)}^2$$

将一次函数带入$h(x_i)$:
$${\theta }_j:={\theta }_j-\alpha \frac{d}{d_{\theta }{\theta }_j}\frac{1}{m}\sum _{i=1}^m({\theta }_1{x}_i+{\theta }_0-y_i{)}^2$$

损失函数$\frac{1}{m}{\sum }_{i=1}^m({\theta }_1{x}_i+{\theta }_0-y_i{)}^2$对于${\theta }_0$的偏导为：
$$j=\frac{1}{m}\sum _{i=1}^{m}2({\theta }_1{x}_i+{\theta }_0-y_i)$$
将${\theta }_0$偏导数带入梯度下降即：
$${\theta }_0:={\theta }_0-\alpha \frac{2}{m}\sum _{i=1}^m(h(x_i)-y_i)$$

损失函数$\frac{1}{m}{\sum }_{i=1}^m({\theta }_1{x}_i+{\theta }_0-y_i{)}^2$对于${\theta }_1$的偏导为：
$$j=\frac{1}{m}\sum _{i=1}^{m}2({\theta }_1{x}_i+{\theta }_0-y_i)x_i$$

将${\theta }_1$偏导数带入梯度下降即：
$${\theta }_1:={\theta }_1-\alpha \frac{2}{m}\sum _{i=1}^m(h(x_i)-y_i)x_i$$

梯度下降算法即不断迭代重复调整${\theta }_0,{\theta }_1$的值，直到收敛，找到最佳拟合函数。

${\theta }_0:={\theta }_0-\alpha \frac{2}{m}{\sum }_{i=1}^m(h(x_i)-y_i)$
${\theta }_1:={\theta }_1-\alpha \frac{2}{m}{\sum }_{i=1}^m(h(x_i)-y_i)x_i$

以上。如有错误请指出。

参考

1.吴恩达机器学习系列课程
2. https://zhuanlan.zhihu.com/p/82470946
3.https://baike.baidu.com/item/%E6%A2%AF%E5%BA%A6%E4%B8%8B%E9%99%8D%E6%B3%95