代码随想录day43｜1049. 最后一块石头的重量 II｜494. 目标和 ｜474.一和零｜Golang

代码随想录day43

无话可说

 1049. 最后一块石头的重量 II

 参考视频：leetcode1049 最后一块石头的重量II 题解_哔哩哔哩_bilibili

 

func lastStoneWeightII(stones []int) int {
    dp := make([]int,15001)
    sum := 0
    for _, v := range stones {
        sum += v 
    }
    target := sum / 2
    for i:=0;i=stones[i];j--{
            dp[j] = max(dp[j], dp[j-stones[i]] + stones[i])
        }
    }
    return sum - 2 * dp[target]
}


func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

 494. 目标和

视频：【300题刷题挑战】leetcode力扣494 目标和 findTargetSumWays 第六十九题 | 动态规划 Dynamic Planning_哔哩哔哩_bilibili

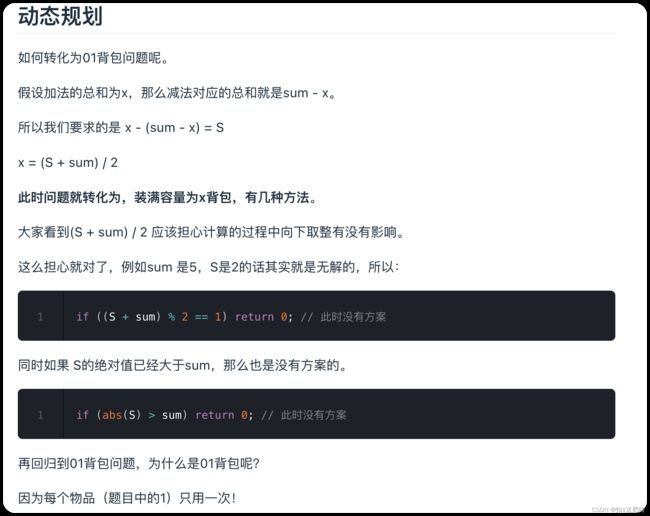这次和之前遇到的背包问题不一样了，之前都是求容量为j的背包，最多能装多少。

本题则是装满有几种方法。其实这就是一个组合问题了。

 

 

代码如下：

func findTargetSumWays(nums []int, target int) int {
	sum := 0
	for _, v := range nums {
		sum += v
	}
	if abs(target) > sum {
		return 0
	}
	if (sum+target)%2 == 1 {
		return 0
	}
	// 计算背包大小
	bag := (sum + target) / 2
	// 定义dp数组
	dp := make([]int, bag+1)
	// 初始化
	dp[0] = 1
	// 遍历顺序
	for i := 0; i < len(nums); i++ {
		for j := bag; j >= nums[i]; j-- {
			//推导公式
			dp[j] += dp[j-nums[i]]
			//fmt.Println(dp)
		}
	}
	return dp[bag]
}

func abs(x int) int {
	if x < 0 {
        return -x 
    }
    return x 
}

474.一和零

        这道题目，还是比较难的，也有点像程序员自己给自己出个脑筋急转弯，程序员何苦为难程序员呢哈哈。

        来说题，本题不少同学会认为是多重背包，一些题解也是这么写的。

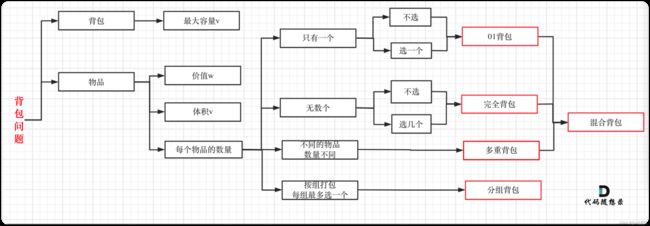
        其实本题并不是多重背包，再来看一下这个图，捋清几种背包的关系

 多重背包是每个物品，数量不同的情况。

        本题中strs 数组里的元素就是物品，每个物品都是一个！而m 和 n相当于是一个背包，两个维度的背包。

        理解成多重背包的同学主要是把m和n混淆为物品了，感觉这是不同数量的物品，所以以为是多重背包。

        但本题其实是01背包问题！

        这不过这个背包有两个维度，一个是m 一个是n，而不同长度的字符串就是不同大小的待装物品。

开始动规五部曲：

1、确定dp数组（dp table）以及下标的含义：

        dp[i][j]：最多有i个0和j个1的strs的最大子集的大小为dp[i][j]。

2、确定递推公式：

        dp[i][j] 可以由前一个strs里的字符串推导出来，strs里的字符串有zeroNum个0，oneNum个1。

        dp[i][j] 就可以是 dp[i - zeroNum][j - oneNum] + 1。

        然后我们在遍历的过程中，取dp[i][j]的最大值。

        所以递推公式：dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);

        此时大家可以回想一下01背包的递推公式：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

        对比一下就会发现，字符串的zeroNum和oneNum相当于物品的重量（weight[i]），字符串本身的个数相当于物品的价值（value[i]）。

        这就是一个典型的01背包！ 只不过物品的重量有了两个维度而已。

3、dp数组如何初始化

        因为物品价值不会是负数，初始为0，保证递推的时候dp[i][j]不会被初始值覆盖。

        在动态规划：关于01背包问题，你该了解这些！（滚动数组）中已经讲解了，01背包的dp数组初始化为0就可以。

        因为物品价值不会是负数，初始为0，保证递推的时候dp[i][j]不会被初始值覆盖。

4、确定遍历顺序：

        在动态规划：关于01背包问题，你该了解这些！（滚动数组）中，我们讲到了01背包为什么一定是外层for循环遍历物品，内层for循环遍历背包容量且从后向前遍历！

        那么本题也是，物品就是strs里的字符串，背包容量就是题目描述中的m和n。

代码如下：

for (string str : strs) { // 遍历物品
    int oneNum = 0, zeroNum = 0;
    for (char c : str) {
        if (c == '0') zeroNum++;
        else oneNum++;
    }
    for (int i = m; i >= zeroNum; i--) { // 遍历背包容量且从后向前遍历！
        for (int j = n; j >= oneNum; j--) {
            dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
        }
    }
}

有同学可能想，那个遍历背包容量的两层for循环先后循序有没有什么讲究？

没讲究，都是物品重量的一个维度，先遍历那个都行！

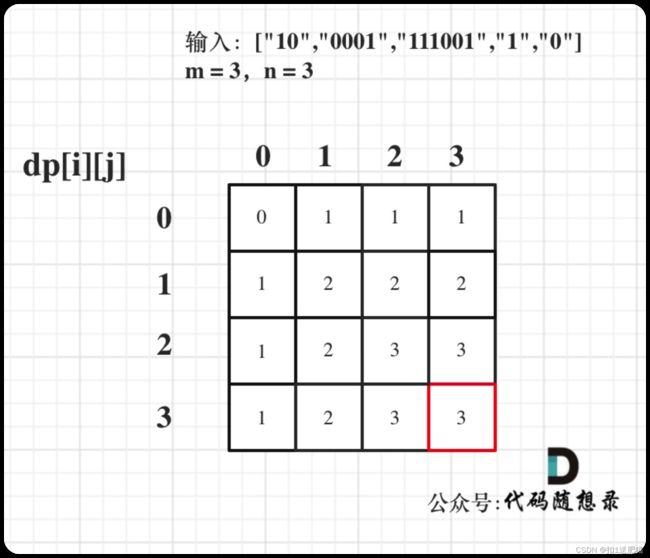
5、举例推导dp数组：

以输入：["10","0001","111001","1","0"]，m = 3，n = 3为例

最后dp数组的状态如下所示：

总结

不少同学刷过这道提，可能没有总结这究竟是什么背包。

这道题的本质是有两个维度的01背包，如果大家认识到这一点，对这道题的理解就比较深入了。

func findMaxForm(strs []string, m int, n int) int {
	// 定义数组
	dp := make([][]int, m+1)
	for i,_ := range dp {
		dp[i] = make([]int, n+1 )
	}
	// 遍历
	for i:=0;i= zeroNum;j-- {
			for k:=n ; k >= oneNum;k-- {
				// 推导公式
				dp[j][k] = max(dp[j][k],dp[j-zeroNum][k-oneNum]+1)
			}
		}
		//fmt.Println(dp)
	}
	return dp[m][n]
}

func max(a,b int) int {
	if a > b {
		return a
	}
	return b
}