关于labuladong算法小抄的贪心算法C++学习拓展笔记（附带一个有趣思想的《过加油站》题目）

贪心之区间调度问题

该问题的解题思想就是：排序+贪心记录

1、找最多不重叠区间

虽说区间有许多数据结构帮忙解决，但是关于区间之间的重叠多少个、去除几个不重叠之类的问题还得靠贪心。其实就是找最早结束的区间，然后通过最早结束的区间把重叠的搞掉，随后继续贪心下去，就是去掉最少的了！
其核心就是四步：
0、先给区间集合 intvs排序，只需要第二维度升序！毕竟只需要比较第二维度和第一维度找交集，千万别排第一维度，因为我们贪心就是找最早结束的，跟最早开始没关系。
1、从区间集合 intvs 中选择一个区间 x，这个 x 是在当前所有区间中结束最早的（end 最小）。
2、把所有与 x 区间相交的区间从区间集合 intvs 中删除，若不重合则更新x为最新的不相交区间(查是否相交，靠区间end和start的比较)
3、重复步骤 1 和 2，直到 intvs 为空为止。之前选出的那些 x 就是最大不相交子集。

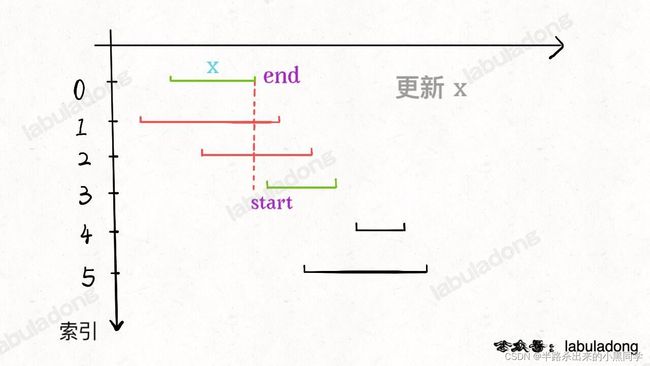
应用 452用最少数量的箭引爆气球

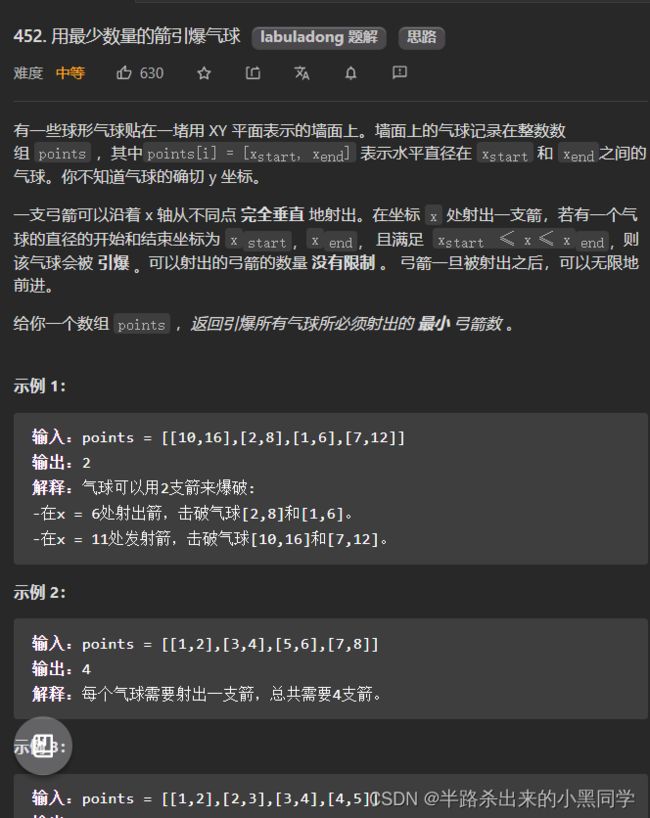
其实就是找到最多不重叠的区间，毕竟重叠的区间可以直接用一根箭射爆。

class Solution {
public:
    int findMinArrowShots(vector<vector<int>>& points) {
        int n = points.size();
        //第0步，先排序
        sort(points.begin(),points.end(),[](const vector<int>&rhs,const vector<int>&abs){return rhs[1]<abs[1];});
        //第1步，找到最初的基准
        int end = points[0][1];
        int ans = 1;
        //第三步，循环开找不重叠
        for(int i=1;i<n;++i)
        {
        	//第二步，找到不重叠，更新基准
            if(end<points[i][0])
            {
                ans++;
                end = points[i][1];
            }
        }
        return ans;
    }
};

【注意】 sort(intervals.begin(),intervals.end(),[](const vector &rhs,const vector &abs){ return rhs[1]这句排序中，如果不加&也会使程序速度大大下降，所以一定要注意细节，必须引用起来！！！

2、找最少几个数可以符合呆在区间中交集为m（以m=2为例）

其实上面那个情况也属于找最少几个数可以呆在交集仅仅1个的区间中的情况。也就是说，上面可以想象到最少找有几个数，可以与每个区间的交集为1。而本题就是，最少有几个数，可以与每个区间的交集为2。
【对什么排序？】上面找一个交集时，从左向右找一个个不重叠的即可，因此只需要对end进行排序； 但是，这个必定是满足交集大于等于2的，因为小区间满足，大区间必然满足，反过来不一定，在左区间相同的情况下,我们取最小区间的两个元素就可以满足所有左区间相同的区间。因此应该对start进行升序排序，对end进行降序排序（常见排序方法）。这样就容易找到小区间了。
【怎么循环？】上面找一个交集时，是根据end来找的，因此需要从前往后循环；而这个找m个交集时，是根据左区间的最小值，也就是说依靠start和start+1，因此就需要从后往前循环。
【怎样贪心记录】前面那个记录一个，只要靠end超过start就是重叠，要不就是不重叠。而由于是两个重叠，那么就有三个状态，不重叠，重叠一个，重叠两个。因此完全可以靠左区间的两个最小值与前一个右区间的最大值，进行判断，来看看是重叠一个还是两个，如下图所示：

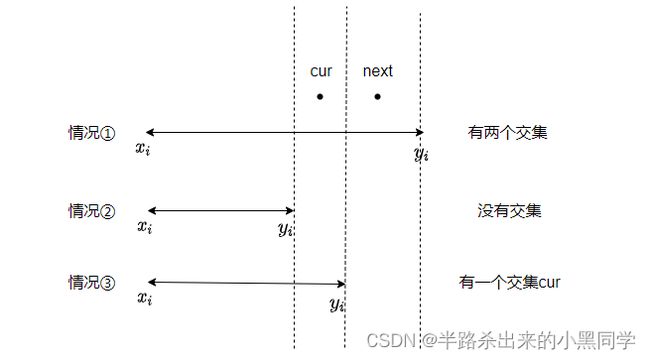
情况1：若已经有两个交集了，那也不用管了，可以继续往下找。这组数看来是符合在这个区间。
情况2：若cur大于前一个的end，那么就是这个情况了，那么应该再添两个数，添的数应该为前一个左区间的start和start+1。这样贪心保证用最少嘛
情况3：若cur小于前一个的end并且next大于前一个的end，那么只需要添加一个数（那肯定就是前一个区间的start）就行了。不过为了下一步的判断，应该把要下一次参与判断的cur和next都更新一下，cur更新为新的start，而next应该更新为cur。
这样就不用全部的点拿去判断，不断替换前一个往前递进判断即可。

应用 757设置交集大小至少为2

class Solution {
public:
    int intersectionSizeTwo(vector<vector<int>>& intervals) {
     int n = intervals.size();
     // 排序
     sort(intervals.begin(),intervals.end(),[](const vector<int>&rhs,const vector<int>&abs)
     {return rhs[0]==abs[0]?rhs[1]>abs[1]:rhs[0]<abs[0];});
      int cur = intervals[n-1][0],next = intervals[n-1][0]+1;
      int ans = 2;
      for(int i=n-2; i>=0; i--)
      {
    	//交集为0
          if(intervals[i][1]<cur)
          {
              ans+=2;
              cur = intervals[i][0];
              next = intervals[i][0]+1;
          }
          //交集为1
          else if(cur<=intervals[i][1] && intervals[i][1]<next)
          {
              ans++;
              next = cur;
              cur = intervals[i][0];
          }
      }
      return ans;
    }
};

3、找到最多有几个重叠区间–上车下车问题

对于这种时间安排的问题，本质上讲就是区间调度问题，十有八九得排序，然后找规律来解决。其实就是利用区间操作，查点大小的方法（详见我的文章线段树整理）——差分数组。但如果差分数组的话，我们最后还要遍历以找到最大点，其实我们可以利用差分数组的思想，来一次解决。
【图例】红色的点代表每个会议的开始时间点，绿色的点代表每个会议的结束时间点。

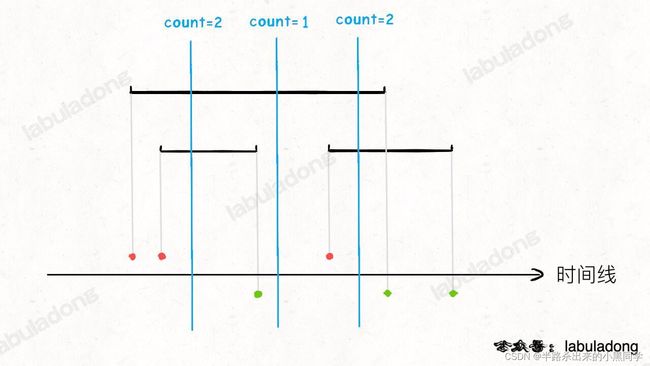
【方法】现在假想有一条带着计数器的线，在时间线上从左至右进行扫描**，每遇到红色的点，计数器 count 加一，每遇到绿色的点，计数器 count 减一**。这样一来，每个时刻有多少个会议在同时进行，就是计数器 count 的值，count 的最大值，就是需要申请的会议室数量。
【实现】也要用到双指针的技巧，其实就是将这些点都分理出来，随后让扫描线一直在两点之间遍历，直到找不到两个点了

class Solution {
public:
    int minMeetingRooms(vector<vector<int>>& intervals) {
    //分别取出来上车的点和下车的点
    vector<int>start,end;
    for(auto & interval:intervals)
    {
        start.push_back(interval[0]);
        end.push_back(interval[1]);
    }
    //排序以方便双指针来找区间
    sort(start.begin(),start.end());
    sort(end.begin(),end.end());
    int ans = 0,count=0;
    int i=0,j=0;
    int n = start.size();
    //用“与”是因为有进就有出，因此进一定先没，没了就铁定减了，就没意义继续下去了
    while(i<n && j<n)
    {
        //双指针模拟跑区间，这个思想一定要明白
        if(start[i]<end[j])
        {
            i++;
            count++;
        }
        else
        {
            j++;
            count--;
        }
        ans = max(ans,count);
    }
    return ans;
    }
};

4、区间可拆，组成一个完整区间

其实核心思路依旧是排序后，画图解决。这里po出例子，简单说一下思路。
1、依旧是区间从小到大排，然后画出图来贪心地选择前面区间能够得到，最长的区间。
2、就这样，不断更新尾部，直到能够到终点就可。

如何运用贪心思想玩跳跃游戏

简单跳跃（经典思想）

每一步都计算一下从当前位置最远能够跳到哪里，然后和一个全局最优的最远位置dis做对比，通过每一步的最优解，更新全局最优解，这就是贪心。
其实正常每次遍历dis即可，不过在遍历之前看看能不能到达这个点，到达这个点后，再更新最远距离即可。如果能够全部遍历，那么就可以返回true了。

class Solution {
public:
    bool canJump(vector<int>& nums) {
        int n = nums.size();
        if(n==1) return true;
        int dis = 0;
        for(int i=0; i<n;i++)
        {
            if(dis<i) return false; 
            dis = max(dis,i+nums[i]);
        }
        return true;
    }
};

一般跳跃（思路简单，模拟难，可学习模拟的思路）

思路其实很简单，就是每次都跳一个能在下一次跳到最远的距离的下标（注意这个最远距离并不是其里面的值，而是i+nums[i]）。就是所谓的贪心嘛。
而在实现的时候，就是对应每次找能跑到的范围（毕竟一开始不知道那个能跳的最远，要对范围内的数进行比较，所以说找范围嘛），而此处的两个变量正好对应着每次跳完后能落在的一个范围。当这个范围能够够到最后一个元素的时候，退出即可！

class Solution {
public:
    int jump(vector<int>& nums) {
        int n = nums.size();
        int ans = 0,start = 0,end = 0;//一开始第0个
        while(end<n-1)//如果范围能够笼罩到最后一个下标即可
        {
            int max_pos = 0;
            for(int i=start;i<=end;i++)
            {
            	//找到最远能够跳到的距离
                max_pos = max(max_pos,nums[i]+i);
            }
            //下一次起跳点范围开始的格子
            start = end+1;
            end = max_pos;
            //上面是更新跳跃至哪的范围，因此跳跃次数应该+1
            ans++;
        }
        return ans;
    }
};

过加油站

其实直接看的话，可以暴力解决，就是从每个点出发，都遍历一次，看看什么时候可以达到要求。但这个题是有技巧的：
我们看看，从一个点出发成功或失败是如何体现的，以
gas = [4,3,1,2,7,4] cost = [1,2,7,3,2,5]，从0出发为例：
【3，1，-6，-1，5，-1】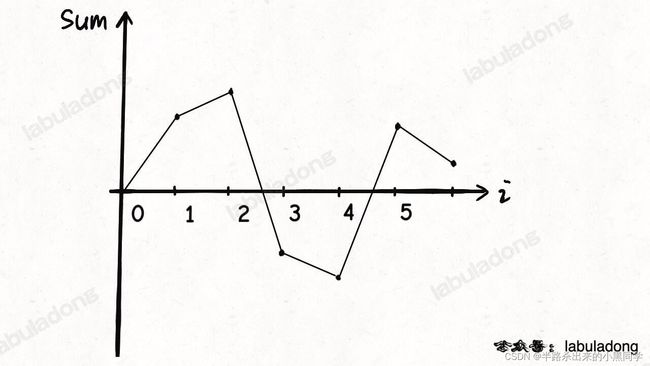
可以看出，当sum有了负值时，不符合我们「累加和一直大于等于 0」的要求，那么就代表无法完成一圈了。因此，如果把这个「最低点」作为起点，就是说将这个点作为坐标轴原点，就相当于把图像「最大限度」向上平移了。
再加上这个数组是环形数组，最低点左侧的图像可以接到图像的最右侧：

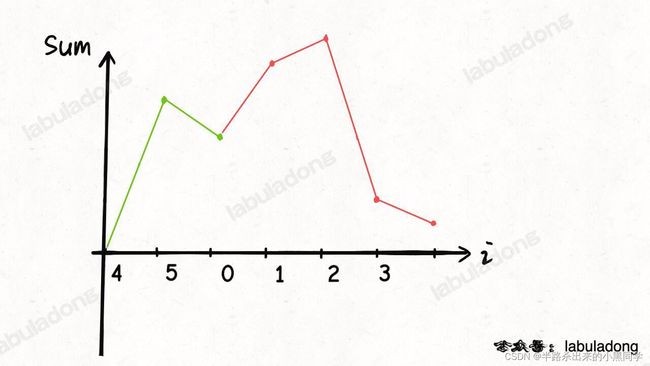
不过，经过平移后图像一定全部在 x 轴以上吗？不一定，因为还有无解的情况：
如果 sum(gas[...]) < sum(cost[...])，总油量小于总的消耗，那肯定是没办法环游所有站点的。
【但此时有几个细节需要注意】
第1个是，要注意加上某值后，其最低点的位置并不是某sum值的位置，而是其+1（如上图可以看出来，虽然i=3的时候是最小值，但其最低点的位置是4）。
第2个就是，因为是环形数组嘛，如果最后其最小的i为n，其实就是第一个位置，也就是0的地方。
要绕过上面那个弯来！代码实现起来较为简单，此处省略。