LeetCode刷题笔记(Java)---第421-440题
文章目录
-
-
- 前言
- 笔记导航
- 421. 数组中两个数的最大异或值
- 423. 从英文中重建数字
- 424. 替换后的最长重复字符
- 427. 建立四叉树
- 429. N叉树的层序遍历
- 430. 扁平化多级双向链表
- 432. 全 O(1) 的数据结构
- 433. 最小基因变化
- 434. 字符串中的单词数
- 435. 无重叠区间
- 436. 寻找右区间
- 437. 路径总和 III
- 438. 找到字符串中所有字母异位词
- 440. 字典序的第K小数字
-
前言
需要开通vip的题目暂时跳过
笔记导航
点击链接可跳转到所有刷题笔记的导航链接
421. 数组中两个数的最大异或值
给定一个非空数组,数组中元素为 a0, a1, a2, … , an-1,其中 0 ≤ ai < 231 。
找到 ai 和aj 最大的异或 (XOR) 运算结果,其中0 ≤ i, j < n 。
你能在O(n)的时间解决这个问题吗?
-
解答
public int findMaximumXOR(int[] nums) { int res = 0; int mask = 0; for (int i = 30; i >= 0; i--) { // 注意点1:注意保留前缀的方法,mask 是这样得来的 // 用异或也是可以的 mask = mask ^ (1 << i); mask = mask | (1 << i); Set<Integer> set = new HashSet<>(); for (int num : nums) { // 注意点2:这里使用 & ,保留前缀的意思(从高位到低位) set.add(num & mask); } // 这里先假定第 n 位为 1 ,前 n-1 位 res 为之前迭代求得 int temp = res | (1 << i); for (Integer prefix : set) { if (set.contains(prefix ^ temp)) { res = temp; break; } } } return res; } -
分析
- 要想结果最大,那么考虑贪心的思想,二进制的高位的1要尽可能的多。
- 异或有这样一个性质 如果A ^ B = C 那么就有 A ^ C = B ,B ^ C = A
- 所以可以按位来判断,最优的解。
- 掩码mask 从 1 << 30
- 遍历数组,每一个数与掩码与运算,保留前缀,放入Set集合当中。
- 贪心思想 假定当前位置是1,遍历set集合,判断是否有set.contains(prefix ^ temp) 也就是 存在两个数的异或结果为 1。更新 答案为假设的答案。
- 重复以上步骤。从高位往低位判断。
-
提交结果
423. 从英文中重建数字
给定一个非空字符串,其中包含字母顺序打乱的英文单词表示的数字0-9。按升序输出原始的数字。
注意:
- 输入只包含小写英文字母。
- 输入保证合法并可以转换为原始的数字,这意味着像 “abc” 或 “zerone” 的输入是不允许的。
- 输入字符串的长度小于 50,000。
-
解答
public String originalDigits(String s) { char[] count = new char[26 + (int)'a']; for(char letter: s.toCharArray()) { count[letter]++; } int[] out = new int[10]; out[0] = count['z']; out[2] = count['w']; out[4] = count['u']; out[6] = count['x']; out[8] = count['g']; out[3] = count['h'] - out[8]; out[5] = count['f'] - out[4]; out[7] = count['s'] - out[6]; out[9] = count['i'] - out[5] - out[6] - out[8]; out[1] = count['n'] - out[7] - 2 * out[9]; StringBuilder output = new StringBuilder(); for(int i = 0; i < 10; i++) for (int j = 0; j < out[i]; j++) output.append(i); return output.toString(); } -
分析
- z,w,u,x,g 这5个字母只在一个数字单词中出现。所以有几个这样的字母就可以确定有多少个对应的数字。
- h 只在3和8中出现,而前一步已经得出了8 的个数。所以count[‘h’] - out[8] 就是数字3的个数
- 下面的情况同理。
-
提交结果
424. 替换后的最长重复字符
给你一个仅由大写英文字母组成的字符串,你可以将任意位置上的字符替换成另外的字符,总共可最多替换 k 次。在执行上述操作后,找到包含重复字母的最长子串的长度。
注意:
字符串长度 和 k 不会超过 104。
-
解答
private int[] map = new int[26]; public int characterReplacement(String s, int k) { if (s == null) { return 0; } char[] chars = s.toCharArray(); int left = 0; int right = 0; int historyCharMax = 0; for (right = 0; right < chars.length; right++) { int index = chars[right] - 'A'; map[index]++; historyCharMax = Math.max(historyCharMax, map[index]); if (right - left + 1 > historyCharMax + k) { map[chars[left] - 'A']--; left++; } } return chars.length - left; } -
分析
- 滑动窗口。一次遍历
- 计算当前数字在滑动窗口内出现的次数。在map中记录
- 计算滑动窗口内出现的重复数字的最大值。
- 如果滑动窗口大于 历史重复数字最大值+k 那么左侧窗口需要右移,当前滑动窗口大小不变。除此之外还需要将移出窗口的那个字符 map记录的次数减1
-
提交结果
427. 建立四叉树
给你一个 n * n 矩阵 grid ,矩阵由若干 0 和 1 组成。请你用四叉树表示该矩阵 grid 。
你需要返回能表示矩阵的 四叉树 的根结点。
注意,当 isLeaf 为 False 时,你可以把 True 或者 False 赋值给节点,两种值都会被判题机制 接受 。
四叉树数据结构中,每个内部节点只有四个子节点。此外,每个节点都有两个属性:
- val:储存叶子结点所代表的区域的值。1 对应 True,0 对应 False;
- isLeaf: 当这个节点是一个叶子结点时为 True,如果它有 4 个子节点则为 False 。
我们可以按以下步骤为二维区域构建四叉树:
- 如果当前网格的值相同(即,全为 0 或者全为 1),将 isLeaf 设为 True ,将 val 设为网格相应的值,并将四个子节点都设为 Null 然后停止。
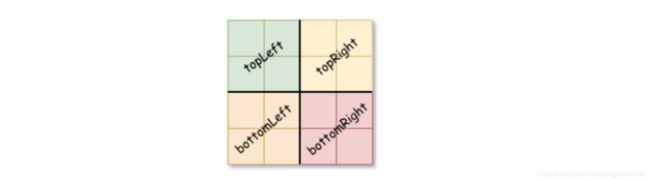
- 如果当前网格的值不同,将 isLeaf 设为 False, 将 val 设为任意值,然后如下图所示,将当前网格划分为四个子网格。
- 使用适当的子网格递归每个子节点。
如果你想了解更多关于四叉树的内容,可以参考 wiki 。
四叉树格式:
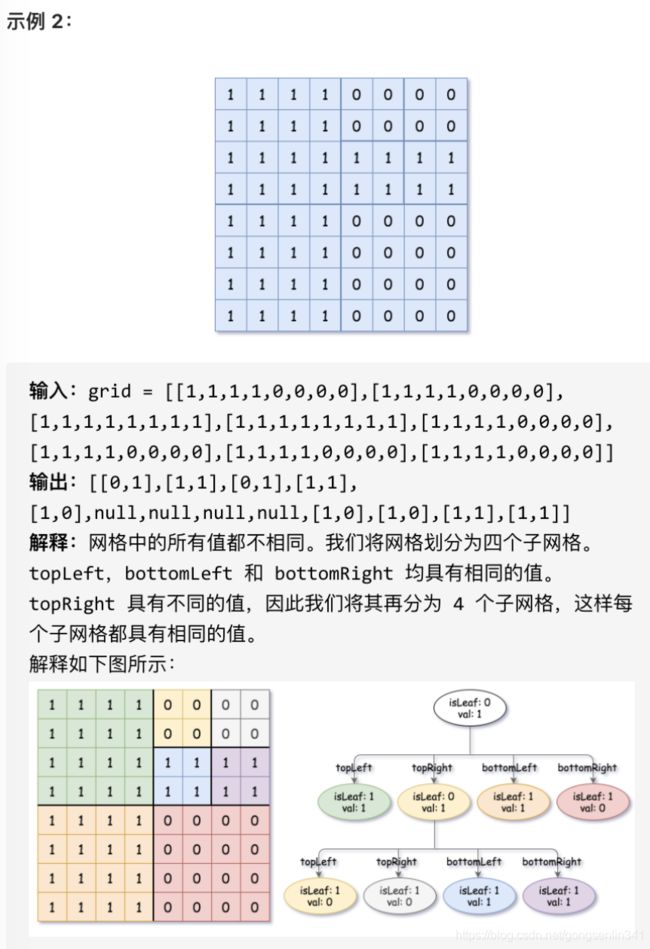
输出为使用层序遍历后四叉树的序列化形式,其中 null 表示路径终止符,其下面不存在节点。
它与二叉树的序列化非常相似。唯一的区别是节点以列表形式表示 [isLeaf, val] 。
如果 isLeaf 或者 val 的值为 True ,则表示它在列表 [isLeaf, val] 中的值为 1 ;如果 isLeaf 或者 val 的值为 False ,则表示值为 0 。
-
解答
public Node construct(int[][] grid) { Node node = construct(grid,0,0,grid.length,grid.length); return node; } public Node construct(int[][] grid,int leftTopRow,int leftTopCol,int rightBottomRow,int rightBottomCol){ if(rightBottomRow == leftTopRow){ boolean val = grid[leftTopRow][leftTopCol] == 1; return new Node(val,true,null,null,null,null); } int cur = grid[leftTopRow][leftTopCol]; boolean flag = false; for(int i = leftTopRow;i < rightBottomRow;i++){ if(flag)break; for(int j = leftTopCol;j < rightBottomCol;j++){ if(grid[i][j] != cur){ flag = true; break; } } } if(!flag){//方块内全部相同 boolean val = cur == 1; return new Node(val,true,null,null,null,null); } // 不同 拆4个 Node topLeft = construct(grid,leftTopRow,leftTopCol,(leftTopRow + rightBottomRow)/2,(leftTopCol + rightBottomCol)/2);//左上 Node topRight = construct(grid,leftTopRow,(leftTopCol+rightBottomCol)/2,(leftTopRow + rightBottomRow)/2,rightBottomCol);//右上 Node bottomLeft = construct(grid,(leftTopRow + rightBottomRow)/2,leftTopCol,rightBottomRow,(leftTopCol+rightBottomCol)/2);//左下 Node bottomRight = construct(grid,(leftTopRow+rightBottomRow)/2,(leftTopCol+rightBottomCol)/2,rightBottomRow,rightBottomCol);//右下 return new Node(true,false,topLeft,topRight,bottomLeft,bottomRight); } -
分析
- 递归实现
- 递归出口1 若当前方格只有一个,那么直接返回 这是叶子结点。
- 遍历范围内的数字,是否相同。如果不同的话,则递归拆分成4个方格
- 若全部相同的话,则这是一个叶子结点,返回。
-
提交结果
429. N叉树的层序遍历
给定一个 N 叉树,返回其节点值的层序遍历。 (即从左到右,逐层遍历)。
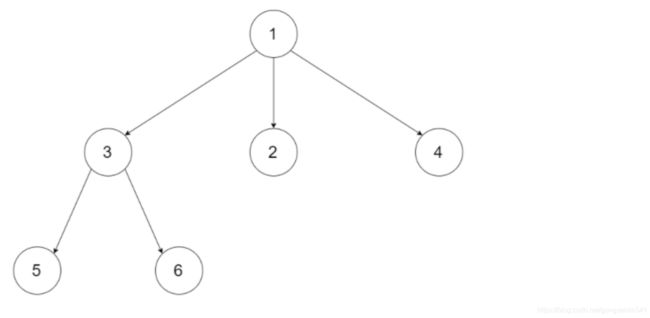
例如,给定一个 3叉树 :
-
解答
public List<List<Integer>> levelOrder(Node root) { List<List<Integer>> res = new ArrayList<>(); if(root == null)return res; Queue<Node> queue = new LinkedList<>(); queue.add(root); while(!queue.isEmpty()){ List<Integer> temp = new ArrayList<>(); Queue<Node> q = new LinkedList<>(); while(!queue.isEmpty()){ Node node = queue.poll(); temp.add(node.val); List<Node> children = node.children; for(Node n:children){ q.offer(n); } } queue = q; res.add(temp); } return res; } -
分析
- 类似二叉树的层次遍历,只是这里需要遍历的子孩子结点
-
提交结果
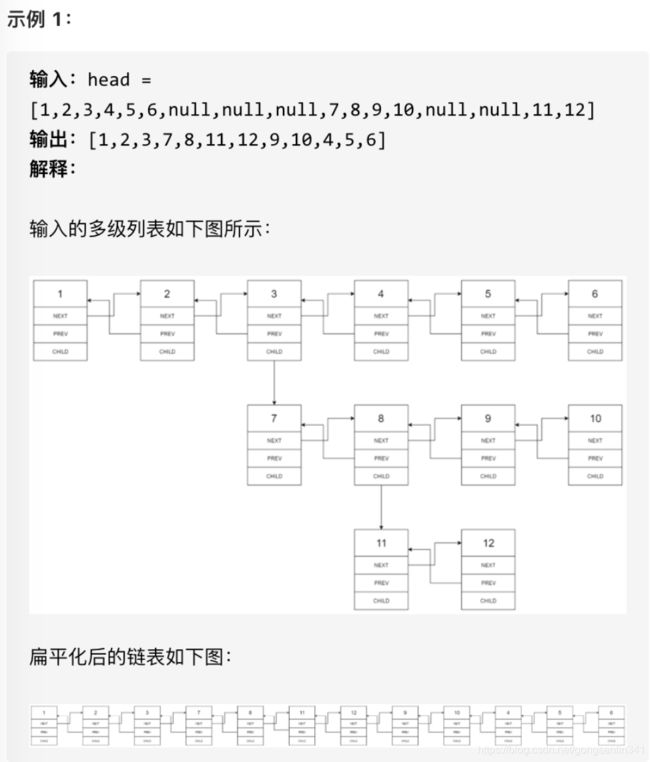
430. 扁平化多级双向链表
多级双向链表中,除了指向下一个节点和前一个节点指针之外,它还有一个子链表指针,可能指向单独的双向链表。这些子列表也可能会有一个或多个自己的子项,依此类推,生成多级数据结构,如下面的示例所示。
给你位于列表第一级的头节点,请你扁平化列表,使所有结点出现在单级双链表中。
提示:
- 节点数目不超过 1000
- 1 <= Node.val <= 10^5
-
解答
public Node flatten(Node head) { if(head == null)return null; return flatten(head,null); } public Node flatten(Node node, Node next) { Node p = node; Node q = null; while (p != null) { if (p.child != null) { Node c = flatten(p.child, p.next); p.next = c; c.prev = p; p.child = null; } q = p; p = p.next; } q.next = next; if(next != null) next.prev = q; return node; } -
分析
- 使用递归的方式,参数是当前链表的头结点,和上一个发现child结点的后继。
- 遍历链表,若存在child则递归的去处理
- 遍历到当前的最后一个结点的时候,最后一个结点和next连接。
-
提交结果
432. 全 O(1) 的数据结构
请你实现一个数据结构支持以下操作:
- Inc(key) - 插入一个新的值为 1 的 key。或者使一个存在的 key 增加一,保证 key 不为空字符串。
- Dec(key) - 如果这个 key 的值是 1,那么把他从数据结构中移除掉。否则使一个存在的 key 值减一。如果这个 key 不存在,这个函数不做任何事情。key 保证不为空字符串。
- GetMaxKey() - 返回 key 中值最大的任意一个。如果没有元素存在,返回一个空字符串"" 。
- GetMinKey() - 返回 key 中值最小的任意一个。如果没有元素存在,返回一个空字符串""。
挑战:
你能够以 O(1) 的时间复杂度实现所有操作吗?
-
解答
class AllOne { // map1保存key-.value 的映射 private Map<String, Integer> map1; // map2保存val->keys 的映射, DLinkedNode为双向链表节点 // map2的作用是为了O(1)时间拿到统计次数对应的链表节点 // 链表中的所有操作只会涉及到前一个节点或者后一个节点,时间也为O(1) private Map<Integer, DLinkedNode> map2; // 双向链表的头, 双向链表从head到tail的value值依次减小 private DLinkedNode head; // 双向链表的尾 private DLinkedNode tail; /** Initialize your data structure here. */ public AllOne() { map1 = new HashMap<>(); map2 = new HashMap<>(); head = new DLinkedNode(0); tail = new DLinkedNode(0); head.next = tail; tail.pre = head; } /** Inserts a new keywith value 1. Or increments an existing key by 1. */ public void inc(String key) { // 如果map1中包含key if (map1.containsKey(key)) { int val = map1.get(key); map1.put(key, val + 1); // 根据value拿到次数更新前的node DLinkedNode node = map2.get(val); // value加一后,从原node的Set中删除key node.keys.remove(key); DLinkedNode preNode = node.pre; // 当前一个node为head或前一个node的次数统计大于val+1时, // 表示还目前没有统计次数为val+1的key, // 此时应该新建一个DLinkedNode,将newNode插入到preNode和node之间,并把key加入到newNode的保存key的Set中 // 同时,将新的统计次数(val+1)和新节点newNode的映射加入到map2中 if (preNode == head || preNode.val > val + 1) { DLinkedNode newNode = new DLinkedNode(val + 1); newNode.keys.add(key); newNode.next = node; newNode.pre = preNode; preNode.next = newNode; node.pre = newNode; map2.put(val + 1, newNode); preNode = newNode; } else { // 如果当前已经有统计次数为val+1的节点,只需key加入到Set中即可 preNode.keys.add(key); } // 如果原节点在移除key后size为0,则删除该节点,并在map2中删除val->node的映射 if (node.keys.size() == 0) { preNode.next = node.next; node.next.pre = preNode; map2.remove(val); } } else { // map1中不包含key map1.put(key, 1); DLinkedNode node = map2.get(1); // 如果当前没有统计次数为1的节点,则新建节点并插入到双向链表的尾部,因为统计次数最小为1 // 并将1->newNode的映射加入到map2中 if (node == null) { DLinkedNode newNode = new DLinkedNode(1); newNode.keys.add(key); newNode.next = tail; newNode.pre = tail.pre; tail.pre.next = newNode; tail.pre = newNode; map2.put(1, newNode); } else { node.keys.add(key); } } } /** Decrements an existing key by 1. If Key's value is 1, remove it from the data structure. */ public void dec(String key) { // 如果map1中包含key,进行处理,否则不做任何操作 if (map1.containsKey(key)) { // 获取当前统计次数 int val = map1.get(key); // 当前统计次数对应的节点 DLinkedNode node = map2.get(val); // 从节点的keys set中移除当前key node.keys.remove(key); // 如果原统计次数为1,从map1中移除当前key if (val == 1) { map1.remove(key); } else { // 更新map1中的统计次数 map1.put(key, val - 1); // 拿到当前节点的下一个节点 DLinkedNode nextNode = node.next; // 如果下一个节点为链表尾部或下一个节点的统计次数小于val-1 // 则新建一个节点,统计次数为val-1,将当前key加入到keys Set中 // 并将新节点插入到当前节点的后面,同时更新map2 if (nextNode == tail || nextNode.val < val - 1) { DLinkedNode newNode = new DLinkedNode(val - 1); newNode.keys.add(key); newNode.pre = node; newNode.next = nextNode; node.next = newNode; nextNode.pre = newNode; map2.put(val - 1, newNode); } else { // 下一个节点的统计次数为val-1,将key加到下一节点的keys Set中 nextNode.keys.add(key); } } // 如果当前节点只包含这一个key,删除后size为0,则将当前节点删除,并更新map2 if (node.keys.size() == 0) { node.pre.next = node.next; node.next.pre = node.pre; map2.remove(val); } } } /** Returns one of the keys with maximal value. */ public String getMaxKey() { // 按照双向链表的定义,如果链表中存在节点(head和tail不算,dummy节点),则对应最大value的keys为head的下一个节点 if (head.next == tail) { return ""; } else { return head.next.keys.iterator().next(); } } /** Returns one of the keys with Minimal value. */ public String getMinKey() { // 按照双向链表的定义,如果链表中存在节点(head和tail不算,dummy节点),则对应最小value的keys为tail的前一个节点 if (tail.pre == head) { return ""; } else { return tail.pre.keys.iterator().next(); } } private class DLinkedNode { int val; Set<String> keys; DLinkedNode pre, next; public DLinkedNode(int val) { this.val = val; this.keys = new HashSet<>(); } } } -
分析
- 维护一个双向链表,链表从小到大排序
-
提交结果
433. 最小基因变化
一条基因序列由一个带有8个字符的字符串表示,其中每个字符都属于 “A”, “C”, “G”, "T"中的任意一个。
假设我们要调查一个基因序列的变化。一次基因变化意味着这个基因序列中的一个字符发生了变化。
例如,基因序列由"AACCGGTT" 变化至 “AACCGGTA” 即发生了一次基因变化。
与此同时,每一次基因变化的结果,都需要是一个合法的基因串,即该结果属于一个基因库。
现在给定3个参数 — start, end, bank,分别代表起始基因序列,目标基因序列及基因库,请找出能够使起始基因序列变化为目标基因序列所需的最少变化次数。如果无法实现目标变化,请返回 -1。
注意:
- 起始基因序列默认是合法的,但是它并不一定会出现在基因库中。
- 所有的目标基因序列必须是合法的。
- 假定起始基因序列与目标基因序列是不一样的。
-
解答
int res = Integer.MAX_VALUE; public int minMutation(String start, String end, String[] bank) { char[][] banks = new char[bank.length][8]; for (int i = 0; i < bank.length; i++) { banks[i] = bank[i].toCharArray(); } solution1(start.toCharArray(), end.toCharArray(), banks, 0); return minChange == Integer.MAX_VALUE ? -1 : minChange; } int minChange = Integer.MAX_VALUE; private void solution1(char[] start, char[] end, char[][] bank, int change) { if (Arrays.equals(start, end)) { minChange = Math.min(minChange, change); return; } for (int j = 0; j < bank.length; j++) { char[] piece = bank[j]; if (piece == null) continue; // 已用过的片段 int diff = 0; // 获取基因库中不同为1的片段,作为改变一次后的新start for (int i = 0; i < start.length; i++) { if (start[i] != piece[i]) diff++; } if (diff == 1) { bank[j] = null; // 置空,防止循环使用 solution1(piece, end, bank, change + 1); bank[j] = piece; // 还原回溯 } } } -
分析
- 回溯实现
- 每次在词典库中寻找与start 只有一个字符不同的字符串,用过的词设置为空。递归。
- 若最后start和end相同,则记录下变换的次数,更新最小值。
- 否则回溯。还原词库
434. 字符串中的单词数
统计字符串中的单词个数,这里的单词指的是连续的不是空格的字符。
请注意,你可以假定字符串里不包括任何不可打印的字符。
-
解答
public int countSegments(String s) { boolean flag = false; int res = 0; for(int i = 0;i < s.length();i++){ char ch = s.charAt(i); if(!flag){ if((ch != ' ')) flag = true; }else{ if(ch == ' '){ res++; flag = false; } } } if(flag)res++; return res; } -
分析
-
用flag 当前遍历的是否是字符
-
如果flag = false 并且当前遍历的是字符,那么就修改flag
-
如果flag等于true 并且 当前遍历的是一个空格,那么就说明当前位置之前的是一个可打印字符串,res++。
并修改flage为false
-
最后遍历结束,还需要判断flag是否是true 如果是的话 结果+1
-
435. 无重叠区间
给定一个区间的集合,找到需要移除区间的最小数量,使剩余区间互不重叠。
注意:
- 可以认为区间的终点总是大于它的起点。
- 区间 [1,2] 和 [2,3] 的边界相互“接触”,但没有相互重叠。
-
解答
public int eraseOverlapIntervals(int[][] intervals) { PriorityQueue<int[]> queue = new PriorityQueue<>(new Comparator<int[]>(){ public int compare(int[] o1,int[] o2){ if(o1[0] != o2[0])return o1[0] - o2[0]; return o2[1] - o1[1]; } }); for(int[] interval : intervals){ queue.add(interval); } int[] last = queue.poll(); int res = 0; while(!queue.isEmpty()){ int[] cur = queue.poll(); if(cur[0] < last[1]){ res++; if(cur[1] < last[1]) last = cur; }else{ last = cur; } } return res; } -
分析
- 利用优先级队列将,根据区间的起始位置升序排列,若区间的起始位置相同,则根据区间的结束位置降序排列。
- 全部区间放入优先队列当中
- 取出队头
- 开始遍历优先级队列。
- 每次遍历的当前区间 和上一个取出的区间进行比较。
- 若当前区间的起始位置小于上一个区间的结束位置,说明他们有重叠。那么此时需要判断哪个区间的结束位置更大,删除结束位置大的,因为结束位置越大 和其他区间的重叠的可能性就越大。删除的操作起始就是比较两个区间的结束位置。如果当前的结束位置小于上一次的结束位置。那么last记录为当前的区间,表示删除了上一个区间。否则last不变,表示删除了当前区间。res++
- 如果当前区间的起始位置大于等于上一个区间的结束位置。那么此时更新last为当前遍历的区间即可。
436. 寻找右区间
给定一组区间,对于每一个区间 i,检查是否存在一个区间 j,它的起始点大于或等于区间 i 的终点,这可以称为 j 在 i 的“右侧”。
对于任何区间,你需要存储的满足条件的区间 j 的最小索引,这意味着区间 j 有最小的起始点可以使其成为“右侧”区间。如果区间 j 不存在,则将区间 i 存储为 -1。最后,你需要输出一个值为存储的区间值的数组。
注意:
- 你可以假设区间的终点总是大于它的起始点。
- 你可以假定这些区间都不具有相同的起始点。
-
解答
public int[] findRightInterval(int[][] intervals) { PriorityQueue<int[]> queue = new PriorityQueue<int[]>(new Comparator<int[]>() { @Override public int compare(int[] o1, int[] o2) { return o1[0] - o2[0]; } }); Map<Integer, Integer> map = new HashMap<>(); for ( int i = 0; i < intervals.length; i++) { map.put(intervals[i][0], i); queue.add(intervals[i]); } int[][] sortedIntervals = new int[intervals.length][2]; for ( int i = 0; i < sortedIntervals.length; i++) { sortedIntervals[i] = queue.poll(); } int[] res = new int[intervals.length]; for ( int i = 0; i < sortedIntervals.length; i++) { int[] curInterval = sortedIntervals[i]; int index = map.get(curInterval[0]); boolean flag = false; for (int j = i + 1; j < sortedIntervals.length; j++) { if (sortedIntervals[j][0] >= curInterval[1]) { int rightIndex = map.get(sortedIntervals[j][0]); res[index] = rightIndex; flag = true; break; } } if(!flag)res[index] = -1; } return res; } -
分析
- 根据左区间进行堆排序,因为左区间是唯一的。
- 顺便记录下当前区间在原来位置的索引
- 遍历排序后的区间
- 往后找到第一个满足条件的右侧区间 就是最小的右侧区间
-
提交结果
437. 路径总和 III
给定一个二叉树,它的每个结点都存放着一个整数值。
找出路径和等于给定数值的路径总数。
路径不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
二叉树不超过1000个节点,且节点数值范围是 [-1000000,1000000] 的整数。
-
解答
int res = 0; public int pathSum(TreeNode root, int sum) { if(root == null)return 0; dfs(root, sum, 0, false); return res; } public void dfs(TreeNode node, int sum, int temp, boolean use) { if (temp + node.val == sum) { res++; } if (node.left != null) { if (!use) dfs(node.left, sum, temp, false); dfs(node.left, sum, temp + node.val, true); } if (node.right != null) { if (!use) dfs(node.right, sum, temp, false); dfs(node.right, sum, temp + node.val, true); } } -
分析
- 先序遍历,dfs第4个参数表示当前路径上的节点是否被选择,选择了一个结点之后,遍历的路径上必须选择结点。确保路径上连续。
- 一开始use为false 可以任意的选择一个结点作为路径选择的开始。
- 当找到路径和为sum时候 结果+1
438. 找到字符串中所有字母异位词
给定一个字符串 s 和一个非空字符串 p,找到 s 中所有是 p 的字母异位词的子串,返回这些子串的起始索引。
字符串只包含小写英文字母,并且字符串 s 和 p 的长度都不超过 20100。
-
解答
public List<Integer> findAnagrams(String s, String p) { List<Integer> res = new ArrayList<>(); int len = p.length(); for(int i = 0;i < s.length() - len + 1;i++){ String subStr = s.substring(i,i+len); if(isOk(subStr,p)){ res.add(i); } } return res; } public boolean isOk(String str,String p){ char[] strChars = str.toCharArray(); char[] pChars = p.toCharArray(); int[] sum = new int[26]; for(int i = 0;i < strChars.length;i++){ sum[strChars[i] - 'a']++; } for(int i = 0;i < pChars.length;i++){ sum[pChars[i] - 'a']--; if(sum[pChars[i] - 'a'] < 0) return false; } return true; } -
分析
- 暴力解决。。。
440. 字典序的第K小数字
给定整数 n 和 k,找到 1 到 n 中字典序第 k 小的数字。
注意:1 ≤ k ≤ n ≤ 109。
-
解答
public int findKthNumber(int n, int k) { int curr = 1; k = k - 1; while (k > 0) { //计算前缀之间的step数 前缀curr开头的数的个数 int steps = getSteps(n, curr, curr + 1); //前缀间距太大,需要深入一层 if (steps > k) { curr *= 10; //多了一个确定节点,继续-1 k -= 1; } //间距太小,需要扩大前缀范围 else { curr += 1; k -= steps; } } return curr; } private int getSteps(int n, long curr, long next) { int steps = 0; while (curr <= n) { steps += Math.min(n + 1, next) - curr; curr *= 10; next *= 10; } return steps; } -
分析
- 前缀树可以看成一颗10叉树
- 每个结点下有0-9的数字结点
- 10叉树的先序遍历可以找到第k个数字。
- 相邻两个结点之间的数字,是左边那个结点为前缀的数字的个数。
- getSteps 求以curr为前缀的数字到next为前缀之间的数字的个数。
- 如果当前遍历的前缀的个数 比k小。说明需要扩大前缀的范围。curr + 1. k减去steps 表示距离k近了steps步。往兄弟结点走一步
- 当前遍历的前缀个数比k大,说明第k个数字一定是以curr开头的。那么此时curr * 10 ,k - 1 往叶子结点走一步。