二叉树OJ题汇总
本专栏内容为:leetcode刷题专栏,记录了leetcode热门题目以及重难点题目的详细记录
博主csdn个人主页:小小unicorn
⏩专栏分类:Leetcode
代码仓库:小小unicorn的代码仓库
关注我带你学习编程知识
二叉树OJ题汇总
- 判断二叉树是否为完全二叉树
- 判断二叉树是否为对称二叉树
- 判断二叉树是否为平衡二叉树
- 判断二叉树是否为单值二叉树
- 判断二叉树是另一棵树的子树
- 判断两颗二叉树是否相同
-
- 解题思路:
- 二叉树的销毁
- 二叉树的深度遍历(接口型题目)
-
- 前序遍历
- 中序遍历
- 后序遍历
- 左叶子之和
-
- 解题思路:
- 代码解决:
- 二叉树遍历(牛客)
-
- 解题思路:
- 代码解决:
判断二叉树是否为完全二叉树
思路(借助一个队列):
1.先把根入队列,然后开始从队头出数据。
2.出队头的数据,把它的左孩子和右孩子依次从队尾入队列(NULL也入队列)。
3.重复进行步骤2,直到读取到的队头数据为NULL时停止入队列。
4.检查队列中剩余数据,若全为NULL,则是完全二叉树;若其中有一个非空的数据,则不是完全二叉树。
![]()
//判断二叉树是否是完全二叉树
bool isCompleteTree(BTNode* root)
{
Queue q;
QueueInit(&q);//初始化队列
if (root != NULL)
QueuePush(&q, root);
while (!QueueEmpty(&q))//当队列不为空时,循环继续
{
BTNode* front = QueueFront(&q);//读取队头元素
QueuePop(&q);//删除队头元素
if (front == NULL)//当读取到空指针时,停止入队操作
break;
QueuePush(&q, front->left);//出队元素的左孩子入队列
QueuePush(&q, front->right);//出队元素的右孩子入队列
}
while (!QueueEmpty(&q))//读取队列中剩余的数据
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front != NULL)//若队列中存在非空指针,则不是完全二叉树
{
QueueDestroy(&q);//销毁队列
return false;
}
}
QueueDestroy(&q);//销毁队列
return true;//若队列中全是空指针,则是完全二叉树
}
判断二叉树是否为对称二叉树
题目来源:101.对称二叉树
题目描述:
给你一个二叉树的根节点 root , 检查它是否轴对称
对称二叉树就是镜像对称。
![]()
要判断某二叉树是否是对称二叉树,则判断其根结点的左子树和右子树是否是镜像对称即可。
因为是镜像对称,所以左子树的遍历方式和右子树的遍历方式是不同的,准确来说,左子树和右子树的遍历是反方向进行的。
//对称二叉树:
bool isSameTree2(BTNode* p, BTNode* q)
{
//都为空
if (p == NULL && q == NULL)
{
return true;
}
//其中一个为空
if (p == NULL || q == NULL)
{
return false;
}
//都不为空
if (p->val != q->val)
{
return false;
}
return isSameTree2(p->left, q->right) && isSameTree2(p->right, q->left);
}
bool isSymmetric(BTNode* root)
{
if (root == NULL)
{
return true;
}
return isSameTree2(root->left, root->right);
}
判断二叉树是否为平衡二叉树
若一棵二叉树的每个结点的左右两个子树的高度差的绝对值不超过1,则称该树为平衡二叉树。
![]()
思路一:
继续拆分子问题:
1.求出左子树的深度。
2.求出右子树的深度。
3.若左子树与右子树的深度差的绝对值不超过1,并且左右子树也是平衡二叉树,则该树是平衡二叉树。
时间复杂度O(N2)
//判断二叉树是否是平衡二叉树
bool isBalanced(BTNode* root)
{
if (root == NULL)//空树是平衡二叉树
return true;
int leftDepth = BinaryTreeMaxDepth(root->left);//求左子树的深度
int rightDepth = BinaryTreeMaxDepth(root->right);//求右子树的深度
//左右子树高度差的绝对值不超过1 && 其左子树是平衡二叉树 && 其右子树是平衡二叉树
return abs(leftDepth - rightDepth) < 2 && isBalanced(root->left) && isBalanced(root->right);
}
思路二:
我们可以采用后序遍历:
1.从叶子结点处开始计算每课子树的高度。(每棵子树的高度 = 左右子树中高度的较大值 + 1)
2.先判断左子树是否是平衡二叉树。
3.再判断右子树是否是平衡二叉树。
4.若左右子树均为平衡二叉树,则返回当前子树的高度给上一层,继续判断上一层的子树是否是平衡二叉树,直到判断到根为止。(若判断过程中,某一棵子树不是平衡二叉树,则该树也就不是平衡二叉树了)
bool _isBalanced(BTNode* root, int* ph)
{
if (root == NULL)//空树是平衡二叉树
{
*ph = 0;//空树返回高度为0
return true;
}
//先判断左子树
int leftHight = 0;
if (_isBalanced(root->left, &leftHight) == false)
return false;
//再判断右子树
int rightHight = 0;
if (_isBalanced(root->right, &rightHight) == false)
return false;
//把左右子树的高度中的较大值+1作为当前树的高度返回给上一层
*ph = Max(leftHight, rightHight) + 1;
return abs(leftHight - rightHight) < 2;//平衡二叉树的条件
}
//判断二叉树是否是平衡二叉树
bool isBalanced(BTNode* root)
{
int hight = 0;
return _isBalanced(root, &hight);
}
判断二叉树是否为单值二叉树
这个题我们可以通过判断二叉树的根与叶子是否相等来解决这个问题,注意要分三种情况:
1.如果是空树,那也是符合情况的,直接返回true。
2.首先满足左子树不为空的条件下,判断左子树的值是否与根相同,相同返回true,不相同返回false.
3.首先满足右子树不为空的条件下,判断右子树的值是否与根相同,相同返回true,不相同返回false.
bool isUnivalTree(BTNode* root)
{
if(root==NULL)
{
return true;
}
if(root->left && root->left->val != root->val)
{
return false;
}
if(root->right && root->right->val != root->val)
{
return false;
}
return isUnivalTree(root->left)&&isUnivalTree(root->right);
}
判断二叉树是另一棵树的子树
题目来源:572.另一颗树的子树
判断 subRoot 是否是二叉树 root 的子树,即检验 root 中是否包含和 subRoot 具有相同结构和结点值的子树,其中 root 和 subRoot 均为非空二叉树。
![]()
思路:
依次判断以 root 中某一个结点为根的子树是否与subRoot相同。
![]()
发现 root 中的某一个子树与 subRoot 相匹配时,便不再继续比较其他子树,所以图中只会比较到序号2就结束比较。
//比较以root和subRoot为根结点的两棵树是否相等
bool Compare(BTNode* root, BTNode* subRoot)
{
if (root == NULL&&subRoot == NULL)//均为空树,相等
return true;
if (root == NULL || subRoot == NULL)//一个为空另一个不为空,不相等
return false;
if (root->val != subRoot->val)//结点的值不同,不相等
return false;
//比较两棵树的子结点
return Compare(root->left, subRoot->left) && Compare(root->right, subRoot->right);
}
//另一个树的子树
bool isSubtree(BTNode* root, BTNode* subRoot)
{
if (root == NULL)//空树,不可能是与subRoot相同(subRoot非空)
return false;
if (Compare(root, subRoot))//以root和subRoot为根,开始比较两棵树是否相同
return true;
//判断root的左孩子和右孩子中是否有某一棵子树与subRoot相同
return isSubtree(root->left, subRoot) || isSubtree(root->right,subRoot);
}
判断两颗二叉树是否相同
题目来源:leetcode100.相同的树
题目描述:
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
解题思路:
判断两棵二叉树是否相同,也可以将其分解为子问题:
1.比较两棵树的根是否相同。
2.比较两根的左子树是否相同。
3.比较两根的右子树是否相同。
代码如下:
bool isSameTree(BTNode* p, BTNode* q)
{
//都为空
if(p==NULL&&q==NULL)
return true;
//其中一个为空
if(p==NULL||q==NULL)
return false;
//都不为空
if(p->val!=q->val)
return false;
return isSameTree(p->left,q->left)&&
isSameTree(p->right,q->right);
}
二叉树的销毁
二叉树的销毁,与其他数据结构的销毁类似,都是一边遍历一边销毁。但是二叉树需要注意销毁结点的顺序,遍历时我们应该选用后序遍历,也就是说,销毁顺序应该为:左子树->右子树->根。
我们必须先将左右子树销毁,最后再销毁根结点,若先销毁根结点,那么其左右子树就无法找到,也就无法销毁了。
//二叉树销毁
void BinaryTreeDestroy(BTNode* root)
{
if (root == NULL)
return;
BinaryTreeDestroy(root->left);//销毁左子树
BinaryTreeDestroy(root->right);//销毁右子树
free(root);//释放根结点
}
二叉树的深度遍历(接口型题目)
接下来所要说的深度遍历与前面会有所不同,我们前面说到的深度遍历是将一棵二叉树遍历,并将遍历结果打印屏幕上(较简单)。
而下面说到的深度遍历是将一棵二叉树进行遍历,并将遍历结果存储到一个动态开辟的数组中,将数组作为函数返回值进行返回。
思路:
1.首先计算二叉树中结点的个数,便于确定动态开辟的数组的大小。
2.遍历二叉树,将遍历结果存储到数组中。
3.返回数组。
前序遍历
题目来源:144.二叉树的前序遍历
代码:
//求树的结点个数
int TreeSize(BTNode* root)
{
return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
//将树中结点的值放入数组
void preorder(BTNode* root, int* a, int* pi)
{
if (root == NULL)//根结点为空,直接返回
return;
a[(*pi)++] = root->val;//先将根结点的值放入数组
preorder(root->left, a, pi);//再将左子树中结点的值放入数组
preorder(root->right, a, pi);//最后将右子树中结点的值放入数组
}
//前序遍历
int* preorderTraversal(BTNode* root, int* returnSize)
{
*returnSize = TreeSize(root);//值的个数等于结点的个数
int* a = (int*)malloc(sizeof(int)*(*returnSize));
int i = 0;
preorder(root, a, &i);//将树中结点的值放入数组
return arr;
}
中序遍历
题目来源:94.二叉树的中序遍历
//求树的结点个数
int TreeSize(BTNode* root)
{
return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
//将树中结点的值放入数组
void inorder(BTNode* root, int* a, int* pi)
{
if (root == NULL)//根结点为空,直接返回
return;
inorder(root->left, a, pi);//先将左子树中结点的值放入数组
a[(*pi)++] = root->val;//再将根结点的值放入数组
inorder(root->right, a, pi);//最后将右子树中结点的值放入数组
}
//中序遍历
int* inorderTraversal(BTNode* root, int* returnSize)
{
*returnSize = TreeSize(root);//值的个数等于结点的个数
int* a = (int*)malloc(sizeof(int)*(*returnSize));
int i = 0;
inorder(root, a, &i);//将树中结点的值放入数组
return arr;
}
后序遍历
题目来源:145.二叉树的后序遍历
//求树的结点个数
int TreeSize(BTNode* root)
{
return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
//将树中结点的值放入数组
void postorder(BTNode* root, int* a, int* pi)
{
if (root == NULL)//根结点为空,直接返回
return;
postorder(root->left, a, pi);//先将左子树中结点的值放入数组
postorder(root->right, a, pi);//再将右子树中结点的值放入数组
a[(*pi)++] = root->val;//最后将根结点的值放入数组
}
//后序遍历
int* postorderTraversal(BTNode* root, int* returnSize)
{
*returnSize = TreeSize(root);//值的个数等于结点的个数
int* a = (int*)malloc(sizeof(int)*(*returnSize));
int i = 0;
postorder(root, a, &i);//将树中结点的值放入数组
return arr;
}
左叶子之和
题目描述:
给定二叉树的根节点 root ,返回所有左叶子之和。
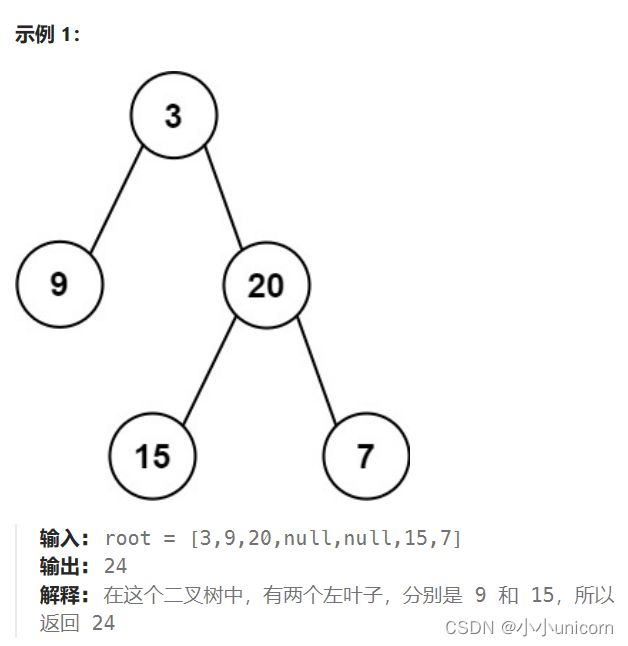
题目来源:leetcode404.左叶子之和
牛客:NC248.左叶子之和
解题思路:
在解决这个问题之前,我们首先要知道什么是叶子节点:
叶子节点:当前节点没有左孩子也没有右孩子
具体解题思路如下:
首先:
判断是否为空树,
如果是空树,返回0;
如果不是空树,判断左孩子节点是否为左叶子节点
然后继续遍历左子树和右子树中的孩子节点,并把结果累加起来。
代码解决:
int sumOfLeftLeaves(struct TreeNode* root )
{
if(root==NULL)
{
return 0;
}
int sum=0;
if(root->left&&root->left->left==NULL&&root->left->right==NULL)
{
sum=root->left->val;
}
return sum+sumOfLeftLeaves(root->left)+sumOfLeftLeaves(root->right);
}
二叉树遍历(牛客)
题目来源:KY11.二叉树遍历(牛客网)
题目描述:
编一个程序,读入用户输入的一串先序遍历字符串,根据此字符串建立一个二叉树(以指针方式存储)。 例如如下的先序遍历字符串: ABC##DE#G##F### 其中“#”表示的是空格,空格字符代表空树。建立起此二叉树以后,再对二叉树进行中序遍历,输出遍历结果。
输入描述:
输入包括1行字符串,长度不超过100。
输出描述:
可能有多组测试数据,对于每组数据, 输出将输入字符串建立二叉树后中序遍历的序列,每个字符后面都有一个空格。 每个输出结果占一行。
解题思路:
根据前序遍历所得到的字符串,我们可以很容易地将其对应的二叉树画出来。
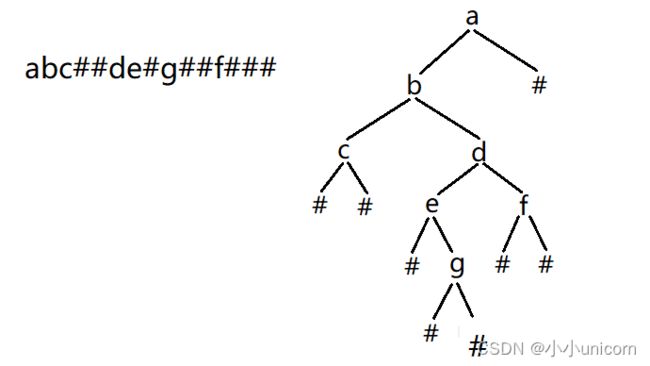
其实很容易发现其中的规律,我们可以依次从字符串读取字符:
1.若该字符不是#,则我们先构建该值的结点,然后递归构建其左子树和右子树。
2.若该字符是#,则说明该位置之下不能再构建结点了,返回即可。
构建完树后,使用中序遍历打印二叉树的数据即可。
代码解决:
#include