math: 四元数与欧拉角（RPY角）的相互转换

1 四元数

1.1 理论基础

在我们能够完全理解四元数之前，我们必须先知道四元数是怎么来的。四元数的根源其实是复数。

四元数的概念是由爱尔兰数学家Sir William Rowan Hamilton发明的, 公式是：

i2=j2=k2=ijk=−1 i 2 = j 2 = k 2 = i j k = − 1

`一般表达式`：

q=w+xi+yj+zk q = w + x i + y j + z k

`性质`：

|q|2=w2+x2+y2+z2=1 | q | 2 = w 2 + x 2 + y 2 + z 2 = 1

其中：i，j，k都是复数。并且通过公式：

i2=j2=k2=ijk i 2 = j 2 = k 2 = i j k

可以推出：

ij=k i j = k

jk=i j k = i

ki=j k i = j

通过公式：

ijk=−1 i j k = − 1

i−1=−i i − 1 = − i

j−1=−j j − 1 = − j

k−1=−k k − 1 = − k

可以推出：

ji=−k j i = − k

kj=−i k j = − i

ik=−j i k = − j

你可能已经注意到了，`i、j、k`之间的`关系`非常像`笛卡尔坐标系下` `单位向量的叉积`规则：

x⃗ ×y⃗ =z⃗  ⟶ y⃗ ×x⃗ =−z⃗  x → × y → = z →   ⟶   y → × x → = − z →

y⃗ ×z⃗ =x⃗  ⟶ z⃗ ×y⃗ =−x⃗  y → × z → = x →   ⟶   z → × y → = − x →

z⃗ ×x⃗ =y⃗  ⟶ x⃗ ×z⃗ =−y⃗  z → × x → = y →   ⟶   x → × z → = − y →

Hamilton自己也发现i、j、k虚数，可以被用来表达3个笛卡尔坐标系的`单位向量`i、j、k，并且仍然保持有虚数的性质，也即： i2=j2=k2=−1 i 2 = j 2 = k 2 = − 1 。

1.1.1 三维空间下：

`向量差乘`即`向量积`可以被定义为： |a⃗ ×b⃗ |=|a⃗ |⋅|b⃗ |⋅sinθ | a → × b → | = | a → | ⋅ | b → | ⋅ sin ⁡ θ

`叉乘(向量的外积)`是物理里面常常用到的概念, 它是由两个向量得到一个新的向量的运算。一般我们都是从`几何意义`下手: 向量 a⃗  a → 和向量 b⃗  b → 叉乘，得到的是一个`垂直于` a⃗  a → 和 b⃗  b → 的向量， c⃗ =a⃗ ×b⃗  c → = a → × b → 它的`方向`由`右手螺旋法则`确定, 它的`长度`是 a⃗  a → 和 b⃗  b → 组成的一个`平行四边形的面积`。 如下图所示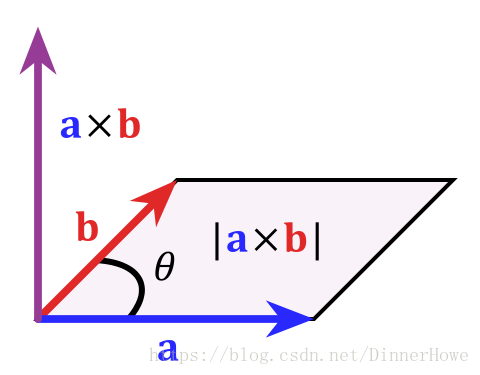：  叉乘满足的基本的性质如下: - a⃗ ×a⃗ =0⃗  a → × a → = 0 → ： 因为夹角是0, 所以平行四边形面积也是0, 即叉积长度为0； - a⃗ ×b⃗ =−(b⃗ ×a⃗ ) a → × b → = − ( b → × a → ) ：等式两边的叉积等大反向, 模长因为平行四边形不变而相同, 方向因为右手法则旋转方向相反而相反； - (λa⃗ )×b⃗ =λ(a⃗ ×b⃗ ) ( λ a → ) × b → = λ ( a → × b → ) ：这点比较好想, 因为: 4. 正数 λ λ 数量乘不会影响 a⃗  a → 的方向, 所以左右的叉积方向一样; 负数 λ λ 使得 a⃗  a → 反向了, 但也使得左右叉积方向相反. 5. 对 a⃗  a → 进行缩放, 平行四边形面积也同等缩放. - (a⃗ +b⃗ )×c⃗ =a⃗ ×c⃗ +b⃗ ×c⃗  ( a → + b → ) × c → = a → × c → + b → × c → ：这最难想象的了放弃

1.1.2 四维空间下：

同理将i、j、k虚数用来表达3个笛卡尔坐标系单位向量X、Y、Z如下图所示：

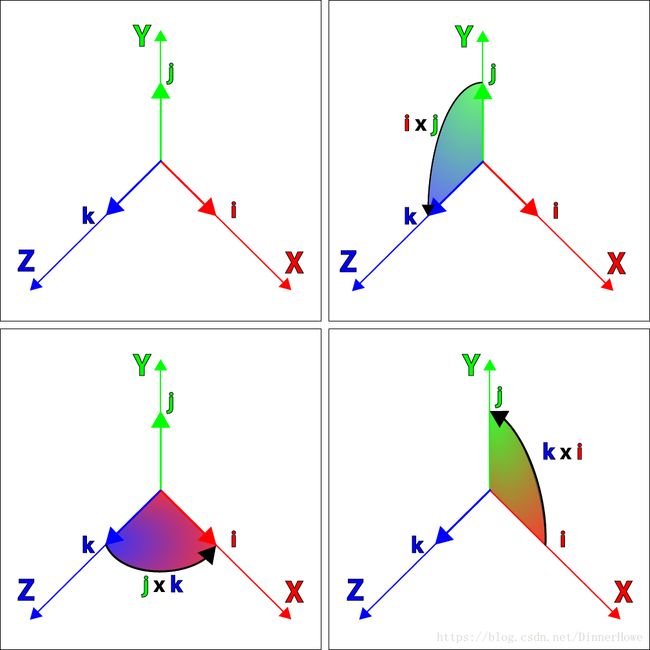
可以得到：

i⃗ ×j⃗ =k⃗  ⟶ j⃗ ×i⃗ =−k⃗  i → × j → = k →   ⟶   j → × i → = − k →

j⃗ ×k⃗ =i⃗  ⟶ k⃗ ×j⃗ =−i⃗  j → × k → = i →   ⟶   k → × j → = − i →

k⃗ ×i⃗ =j⃗  ⟶ i⃗ ×k⃗ =−j⃗  k → × i → = j →   ⟶   i → × k → = − j →

至此，可以将四元素看作空间中任意一个向量了，为了简便，使用有序对的形式表示一个四元素：

q=w+xi+yj+zk ⟶ [w,v⃗ ] q = w + x i + y j + z k   ⟶   [ w , v → ]

其中向量 v⃗  v → 有 xi+yj+zk x i + y j + z k ，x ，y，z轴3个方向的分量。

1.1.3 四元数加减：

和复数类似，四元数也可以被加减，假设有两个向量：

qa=[wa,a⃗ ] q a = [ w a , a → ] qb=[wb,b⃗ ] q b = [ w b , b → ]

于是有

qa+qb=[wa+wb,a⃗ +b⃗ ] q a + q b = [ w a + w b , a → + b → ] qa−qb=[wa−wb,a⃗ −b⃗ ] q a − q b = [ w a − w b , a → − b → ]

1.1.4 四元数的积：

qaqb=[wa,a⃗ ][wb,b⃗ ] q a q b = [ w a , a → ] [ w b , b → ] =(wa+xai+yaj+zak)(wb+xbi+ybj+zbk) = ( w a + x a i + y a j + z a k ) ( w b + x b i + y b j + z b k ) =(wawb−xaxb−yayb−zazb) = ( w a w b − x a x b − y a y b − z a z b ) +(waxb+wbxa+yazb+ybza)i + ( w a x b + w b x a + y a z b + y b z a ) i +(wayb+wbya+zaxb+zbxa)j + ( w a y b + w b y a + z a x b + z b x a ) j +(wazb+wbza+xayb+xbya)k + ( w a z b + w b z a + x a y b + x b y a ) k

2. 欧拉角

首先介绍roll，pitch，yaw的概念：

2.1 Roll:横滚

2.2 Pitch: 俯仰

2.3 Yaw: 偏航（航向）

在无人车或者机器上主要考虑的是Yaw偏航/航向角，因此这里不全部公式偏向于对yaw角的转换计算。

3. 四元数转欧拉角

假设有一个四元数的向量： Q(x,y,z,w) Q ( x , y , z , w ) ，绕轴 A（ax，ay，az） A （ a x ， a y ， a z ） 旋转一个固定角度 α α , 将该动作分解为绕x，y，z（即 ax，ay，az a x ， a y ， a z ）轴旋转角度roll，yaw，pitch，有以下公式：

|q|2=w2+x2+y2+z2=1 | q | 2 = w 2 + x 2 + y 2 + z 2 = 1

⎡⎣⎢⎢rollpithyaw⎤⎦⎥⎥=⎡⎣⎢⎢ϕθψ⎤⎦⎥⎥=⎡⎣⎢⎢⎢⎢atan2(2(zy+wx)w2−x2−y2+z2)arcsin(a(wy−xz))atan2(2(xy+wz)w2+x2−y2−z2)⎤⎦⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢atan2(2(zy+wx)1−2(x2+y2）)arcsin(a(wy−xz))atan2(2(xy+wz)1−2(y2+z2）)⎤⎦⎥⎥⎥⎥ [ r o l l p i t h y a w ] = [ ϕ θ ψ ] = [ a t a n 2 ( 2 ( z y + w x ) w 2 − x 2 − y 2 + z 2 ) arcsin ⁡ ( a ( w y − x z ) ) a t a n 2 ( 2 ( x y + w z ) w 2 + x 2 − y 2 − z 2 ) ] = [ a t a n 2 ( 2 ( z y + w x ) 1 − 2 ( x 2 + y 2 ） ) arcsin ⁡ ( a ( w y − x z ) ) a t a n 2 ( 2 ( x y + w z ) 1 − 2 ( y 2 + z 2 ） ) ]

由于：

1−2(x2+y2）=w2−x2−y2+z2 1 − 2 ( x 2 + y 2 ） = w 2 − x 2 − y 2 + z 2
1−2(y2+z2）=w2+x2−y2−z2 1 − 2 ( y 2 + z 2 ） = w 2 + x 2 − y 2 − z 2

PS：这里不用 arctan arctan 是因为： arctan arctan 和 arcsin arcsin 的结果是 [−π2π2] [ − π 2 π 2 ] ， 这并不能覆盖所有朝向(仅仅对于 pith角 θ θ ， [−π2π2] [ − π 2 π 2 ] 的取值范围满足，但是我们主要考虑的是yaw角)，因此需要用atan2 来代替 arctan arctan 。

4. 欧拉角转四元数

4.1 转化公式

用 Q(x,y,z,w) Q ( x , y , z , w ) 表示一个四元数的向量，绕轴 A（ax，ay，az） A （ a x ， a y ， a z ） 旋转角度 α α 有以下公式：
完整公式：

q=⎡⎣⎢⎢⎢⎢wxyz⎤⎦⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢cos(ϕ/2)cos(θ/2)cos(ψ/2)+sin(ϕ/2)sin(θ/2)sin(ψ/2)sin(ϕ/2)cos(θ/2)cos(ψ/2)−cos(ϕ/2)sin(θ/2)sin(ψ/2)cos(ϕ/2)sin(θ/2)cos(ψ/2)+sin(ϕ/2)cos(θ/2)sin(ψ/2)cos(ϕ/2)cos(θ/2)sin(ψ/2)−sin(ϕ/2)sin(θ/2)cos(ψ/2)⎤⎦⎥⎥⎥⎥ q = [ w x y z ] = [ cos ⁡ ( ϕ / 2 ) cos ⁡ ( θ / 2 ) cos ⁡ ( ψ / 2 ) + sin ⁡ ( ϕ / 2 ) sin ⁡ ( θ / 2 ) sin ⁡ ( ψ / 2 ) sin ⁡ ( ϕ / 2 ) cos ⁡ ( θ / 2 ) cos ⁡ ( ψ / 2 ) − cos ⁡ ( ϕ / 2 ) sin ⁡ ( θ / 2 ) sin ⁡ ( ψ / 2 ) cos ⁡ ( ϕ / 2 ) sin ⁡ ( θ / 2 ) cos ⁡ ( ψ / 2 ) + sin ⁡ ( ϕ / 2 ) cos ⁡ ( θ / 2 ) sin ⁡ ( ψ / 2 ) cos ⁡ ( ϕ / 2 ) cos ⁡ ( θ / 2 ) sin ⁡ ( ψ / 2 ) − sin ⁡ ( ϕ / 2 ) sin ⁡ ( θ / 2 ) cos ⁡ ( ψ / 2 ) ]

如若只绕`z轴旋转`简化公式：

w=cos(α/2) w = cos ⁡ ( α / 2 ) x=sin(α/2)∗cos(βx) x = sin ⁡ ( α / 2 ) ∗ cos ⁡ ( β x ) y=sin(α/2)∗cos(βy) y = sin ⁡ ( α / 2 ) ∗ cos ⁡ ( β y ) z=sin(α/2)∗cos(βz) z = sin ⁡ ( α / 2 ) ∗ cos ⁡ ( β z )

其中 α α 是绕旋转轴旋转的角度， cos(βx) cos ⁡ ( β x ) , cos(βy) cos ⁡ ( β y ) , cos(βz) cos ⁡ ( β z ) 分别为旋转轴在x,y,z方向的分量（由此确定了旋转轴），这里绕z轴旋转，因此 cos(βx)=0 cos ⁡ ( β x ) = 0 并且 cos(βy)=0 cos ⁡ ( β y ) = 0 ， cos(βz)=1 cos ⁡ ( β z ) = 1 。

5. 代码实例

 void eulerAnglesToQuaternion(void) 
{ 
    cosRoll = cosf(roll * 0.5f); 
    sinRoll = sinf(roll * 0.5f);

    cosPitch = cosf(pitch * 0.5f);
    sinPitch = sinf(pitch * 0.5f);

    cosHeading = cosf(hdg * 0.5f);
    sinHeading = sinf(hdg * 0.5f);

    q0 = cosRoll * cosPitch * cosHeading + sinRoll * sinPitch * sinHeading;
    q1 = sinRoll * cosPitch * cosHeading - cosRoll * sinPitch * sinHeading;
    q2 = cosRoll * sinPitch * cosHeading + sinRoll * cosPitch * sinHeading;
    q3 = cosRoll * cosPitch * sinHeading - sinRoll * sinPitch * cosHeading; 
}

void quaternionToRotationMatrix(void) 
{ 
    float q1q1 = sq(q1); 
    float q2q2 = sq(q2); 
    float q3q3 = sq(q3);

    float q0q1 = q0 * q1;
    float q0q2 = q0 * q2;
    float q0q3 = q0 * q3;
    float q1q2 = q1 * q2;
    float q1q3 = q1 * q3;
    float q2q3 = q2 * q3;

    rMat[0][0] = 1.0f - 2.0f * q2q2 - 2.0f * q3q3;
    rMat[0][1] = 2.0f * (q1q2 + -q0q3);
    rMat[0][2] = 2.0f * (q1q3 - -q0q2);

    rMat[1][0] = 2.0f * (q1q2 - -q0q3);
    rMat[1][1] = 1.0f - 2.0f * q1q1 - 2.0f * q3q3;
    rMat[1][2] = 2.0f * (q2q3 + -q0q1);

    rMat[2][0] = 2.0f * (q1q3 + -q0q2);
    rMat[2][1] = 2.0f * (q2q3 - -q0q1);
    rMat[2][2] = 1.0f - 2.0f * q1q1 - 2.0f * q2q2;
}

void quaternionToEulerAngles(void) 
{ 
    roll = atan2f(2.f * (q2q3 + q0q1), q0q0 - q1q1 - q2q2 + q3q3); 
    pitch = asinf(2.f * (q0q2 - q1q3)); 
    yaw = atan2f(2.f * (q1q2 + q0q3), q0q0 + q1q1 - q2q2 - q3q3); 
}

参考：

https://en.wikipedia.org/wiki/Cross_product
https://www.3dgep.com/understanding-quaternions/
https://www.cnblogs.com/zzdyyy/p/7643267.html
https://blog.csdn.net/hziee_/article/details/1630116